中马友谊大桥浅滩区桩基础承台破碎波荷载数值研究*

刘景红,高宁波,李 宁

(1.中交第二航务工程局有限公司,湖北 武汉 430040;2.长大桥梁建设施工交通行业重点实验室,湖北 武汉 430040;3.交通运输行业交通基础设施智能制造技术研发中心,湖北 武汉 430040;4.中交公路长大桥建设国家工程研究中心有限公司,北京 100120)

0 引言

随着工程建设与社会经济的发展,桥梁建造逐渐从内河转向外海峡湾地区。桩基础承台由于其结构轻便、施工简单、荷载传递机理清晰,被广泛应用于外海桥梁等工程结构。桥梁在施工建造及运营期间会面临复杂的海洋环境,如极端台风、波浪、水流等影响,尤其是浅滩区由于地形变化,导致波浪出现翻卷破碎引起的破碎波,给桥梁基础带来巨大危害,且相关规范对破碎波荷载缺少研究,因此亟需开展破碎波对桥梁桩基础承台结构的作用研究,为相关设计与施工提供科学依据。

针对圆柱结构波浪荷载,Morison［1］将圆柱结构受到的波浪荷载分解为质量力与阻力两部分,并通过大量试验给出了圆柱结构的质量力系数与阻力系数。李炎保［2］研究了浅水破碎波对直立圆柱作用力,认为破碎波与桩柱作用过程中在不完全绕流区将出现由于附加质量迅速变化引起的冲击力和桩柱前后波面高度差引起的附加压差力,并归纳了计算桩柱破波力的经验公式。Wienke［3］采用模型试验研究了垂直和倾斜桩柱在破碎波作用下的砰击荷载作用。吕宝柱等［4］研究了破碎波作用下直立堤的运动及稳定性。高学平等［5］认为破碎波在静水面以上对桩柱的冲击力和静水面以下的绕流力的机制是统一的,在计算冲击力时,水的压缩性可忽略,可简单用动量原理估算破碎波对桩柱的冲击荷载。

随着计算资源及数值模拟技术的发展,越来越多的学者采用数值方法研究破碎波。王修亭等［6］基于CFD数值方法研究了单桩破碎波浪荷载,认为Morison公式不适用于浅水区单桩破碎波浪荷载计算。魏凯等［7］基于计算流体力学(CFD)理论,建立逐渐浅化地形的三维数值波浪水池,研究了不同入射波高和周期下破碎波浪特性,分析了不同长宽比圆端形桥墩在不同入射波高作用下的荷载和流场变化。

本文基于CFD方法,建立数值波浪水池,采用聚焦波近似模拟破碎波,研究中马友谊大桥浅滩区桩基础承台波浪荷载,重点关注桩基础承台结构水平与垂向力随着波浪破碎阶段的变化趋势以及迎浪侧波浪砰击荷载。

1 工程概况

中马友谊大桥工程位于北马累环礁东南部,连接首都马累岛和机场岛,位于Gaadhoo Koa海峡之间,大桥所处位置海底地形如图1所示。大桥主要采用桩基础承台结构,引桥浅水区为方形承台,采用钢吊箱施工工艺。受海底地形及峡湾影响,引桥浅水区波浪翻卷破碎现象突出,波浪砰击钢吊箱现象频发,多次引起吊箱结构损坏,给施工带来了极大的不利影响,因而有必要计算近岸破碎波对桩基础吊箱结构的波浪荷载。

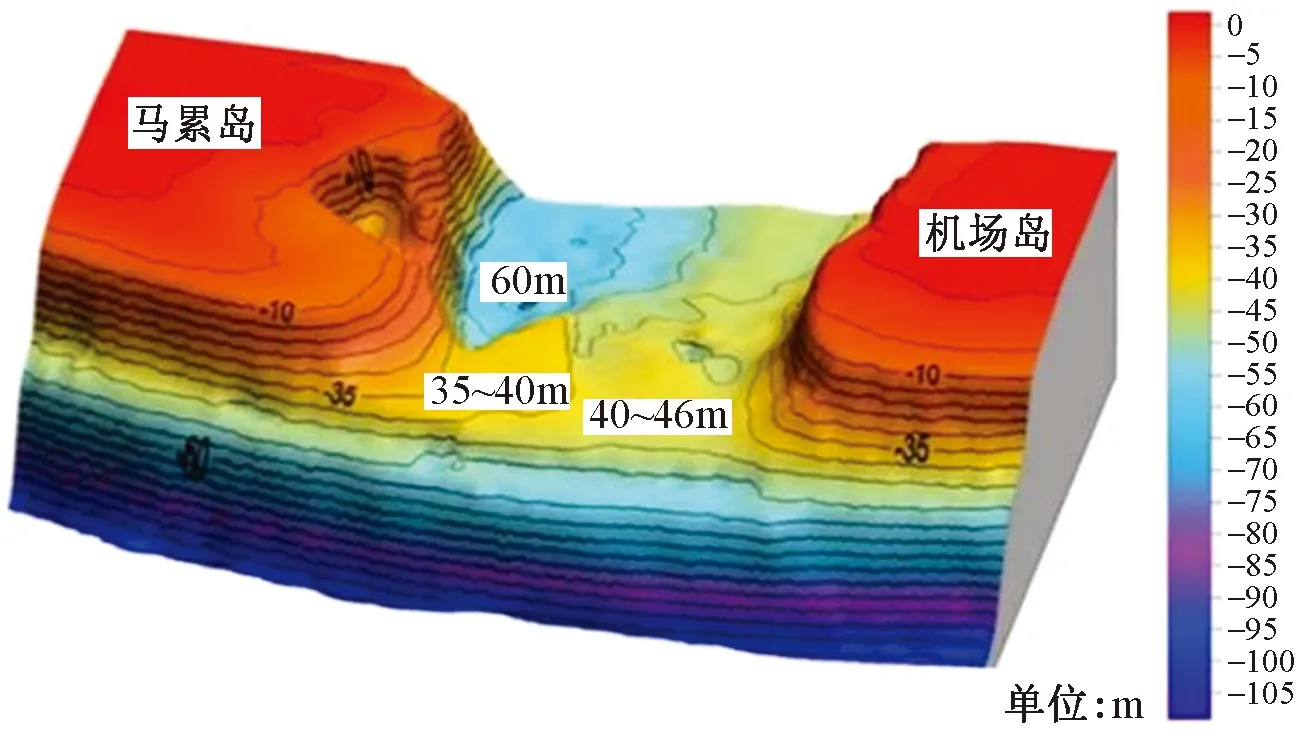
图1 中马友谊大桥项目海底地形Fig.1 Topographic sketch of China-Maldives Friendship Bridge

2 数值模型

2.1 控制方程

本研究控制方程包括连续性方程与动量方程：

·V=0

(1)

(2)

式中：V=(u,v,w),与t分别代表速度矢量与时间;p与F表示压强与外部力(包括重力);ρ与μ分别为水的密度和黏度。

体积分数(volume of fraction,VOF)用来捕捉自由液面,该体积分数αq(x,y,z,t)控制方程如下：

(3)

式中：θq=0,单元是空的;θq=1,单元是满的;0<θq<1,单元包括自由液面。假定θq=0.5为自由液面位置。

2.2 聚焦波模型

波浪破碎的诱因有多重假设,包括地形影响、波浪传播演化过程中非线性的影响等,破碎波研究的一个难点就是如何精准复演波浪破碎的时间及地点。大多数国内外学者［7-8］采用模拟近岸浅滩斜坡来模拟破碎波,本研究中基于聚焦波近似模拟波浪达到最大波高后传播演化破碎过程。Tromans等［9］提出一种“NewWave”的聚焦波模型并被许多学者用来近似模拟海上极端波浪［10-11］,表达式如下：

(4)

图2 典型聚焦波时历Fig.2 Typical focusing wave series

2.3 数值波浪水池

数值波浪水池几何与网格模型如图3所示,水池长10m,目标聚焦位置距离坐标造波边界3.9m,水深为1m,在目标聚焦位置设置一系列虚拟浪高仪,监测波浪传播过程中的变化。

水池左侧为造波边界,本文中基于速度入口造波,在该边界上定义水质点水平速度与垂直速度;底部与右端为固体壁面边界条件;上部为压力入口边界,允许流体从该边界通过;水池右端设置1段消波区,定义1个参数c(x),逐步将消波区内水的黏度从1.003×10-3Pa·s增加到800Pa·s,c(x)表达式如下：

(5)

式中：xL与xR分别代表消波区左边与右边边界水平坐标。

2.4 模型验证

在进行数值仿真分析之前需要开展数值模型验证性研究,确保数值结果的有效性。基于文献［10］中试验数据,选取输入波高A=0.055m开展数值分析,数值结果与试验结果对比如图4所示。由图4可知,数值结果与试验结果吻合良好,验证了本研究中数值模型的有效性。

图4 数值结果与试验结果对比Fig.4 Comparison of numerical results and experimental results

3 模拟聚焦波列

以输入波高A=0.07m为目标最大波高,周期带宽为0.5～1.5s,成分波数量0.5～1.5s,造波边界处水平与垂直速度定义如下：

(6)

(7)

聚焦波群传播演化过程如图5所示,发现在预先设定的聚焦位置(x=3.9m)波高未达到最大,这是由于波浪在传播过程中不同频率成分波相互影响,导致波浪聚焦位置与时间均发生“后移”,经过分析波浪大致聚焦位置为x=4.2m,聚焦波达到最大波高后,波浪开始出现轻微翻卷及破碎。

图5 聚焦波传播演化过程Fig.5 The propagation process of focusing wave

4 桩基础承台波浪荷载分析

4.1 单桩结构破碎波荷载

首先针对单桩结构进行数值模拟,桩基础模型尺度条件下直径为0.1m,缩尺比为30,对应的实尺度桩基础直径为3m。单桩几何与网格模型如图6所示,桩基础位置分别位于x=4.3m与x=4.4m处。单桩结构在破碎波作用下水平波浪力结果与Morison经验值对比分析如图7所示,由图可知聚焦波达到最大波高开始翻卷时水平波浪力最大,约为260kN。随着桩位距离后移,水平波浪力呈减小趋势,但传统计算圆柱结构波浪荷载的Morison经验公式低估破碎波荷载约50%,这证明了Morison经验公式并不完全适用计算桩基础破碎波浪力,建议针对近岸浅滩区桩基础破碎波浪力可在Morison经验值的基础上适当乘以1.5倍的放大系数。

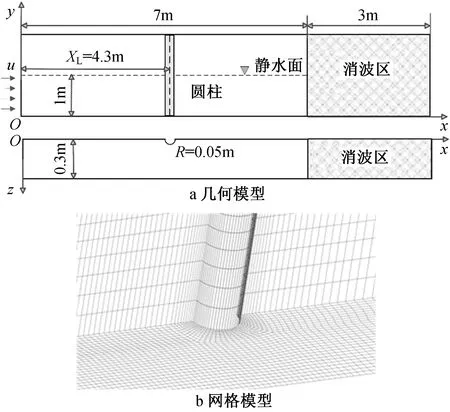
图6 桩基础几何与网格模型Fig.6 Geometry and mesh models of the pile foundation

图7 数值计算结果与Morison经验值对比Fig.7 Comparison of numerical results and Morison results

4.2 承台结构破碎波荷载

浅滩区桥梁基础承台结构多采用规则方形断面形式,中马友谊大桥引桥区承台实际尺寸为长6m,高2.5m,浅水最大波高不超过2.3m,缩尺比为30。为节约计算资源,建立二维简化几何与网格模型(见图8),为验证波浪达到最大波高后翻卷不同阶段时承台波浪荷载变化趋势,分别将承台结构放置于4.3,4.35,4.40,4.45m 4个不同位置处,其对应的实际尺度间距为1.5m。同时在承台正面竖向布置6个压力监测点,竖向布置位置为1.03～1.13m,间隔0.02m,分别命名为点1～6。

图8 承台二维断面结构几何与网格模型Fig.8 Geometry and grid models of 2D section of cap

方形吊箱结构受到的水平和竖向波浪力如图9所示。由图9可知,方形吊箱前沿位于聚焦波群生成位置时竖向荷载最大,约为509kN,而此时水平荷载为288kN;最大水平力发生在聚焦波生成位置后移约0.05～0.1m(实际尺度为1.5～3.0m),值为316kN,此时垂向力约为435kN。同时,由图可知最大水平力和垂向力作用时间短促(<1s),是一种非常瞬态的物理现象,能够引起巨大的动量冲击。不同位置处压力如图10所示,由图10可知最大压强出现在波峰达到最大位置,且出现翻卷破碎时,约为34kPa,大于波浪动压力理论值(PD=ρgAmax)。对于钢吊箱结构一般推荐采用趸船模型计算其波浪荷载［12］(见图11),趸船模型仅能计算钢吊箱结构水平波浪荷载,而无法计算垂向荷载,通过计算分析得到趸船模型下钢吊箱受到的水平波浪力为177kN,远小于CFD模拟结果,说明趸船模型低估了浅水破碎波对钢吊箱荷载,这也是浅水区引桥吊箱施工时,根据规范设计的吊箱结构在波浪作用下多次发生破坏的原因,后续施工过程中有针对性对钢吊箱进行了结构强化。

图9 吊箱结构水平与竖向波浪力(实际尺度)Fig.9 Horizontal and vertical forces of cofferdam structure (in real scale)

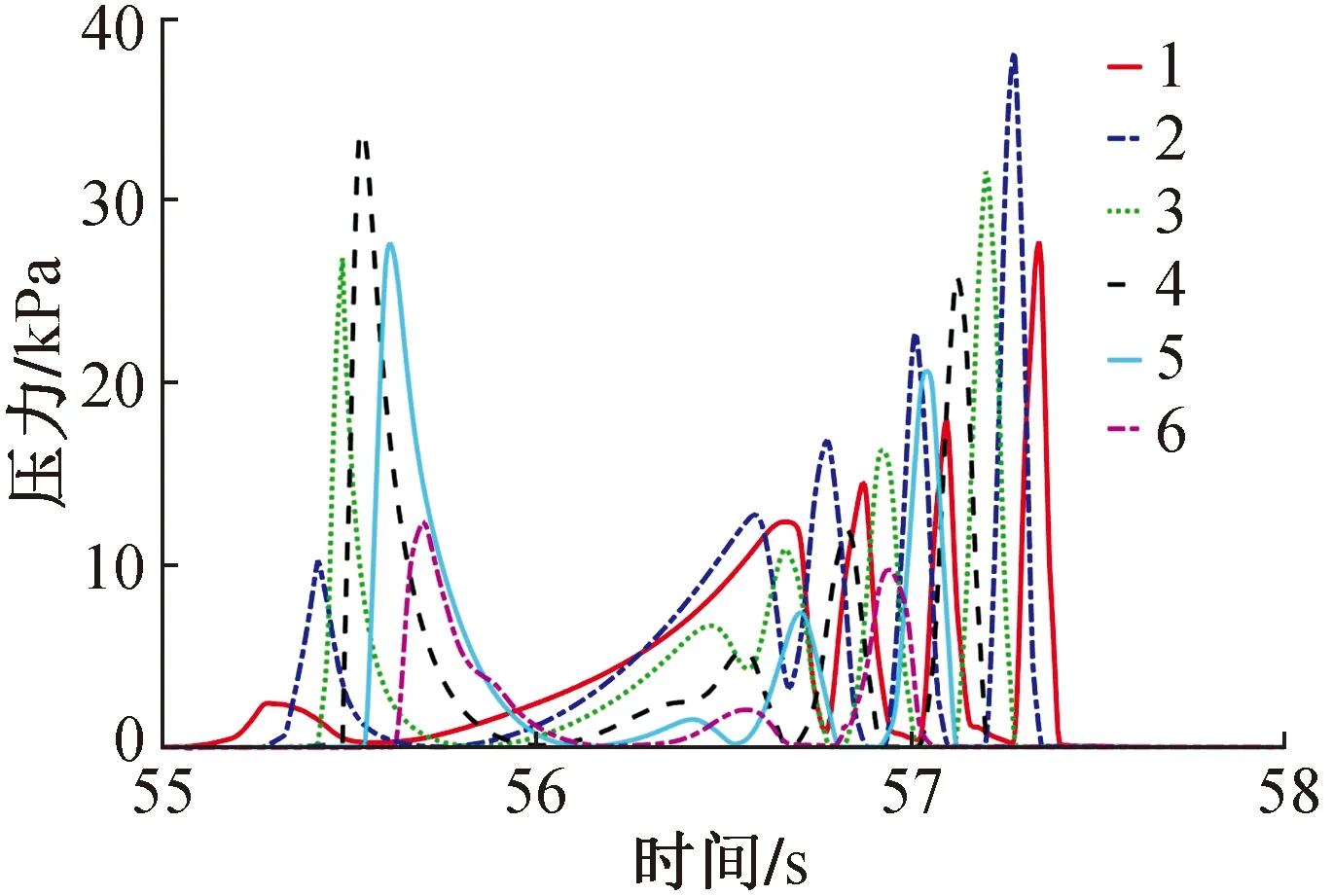
图10 承台竖向不同位置处压力Fig.10 Pressure at different vertical positions of the cap

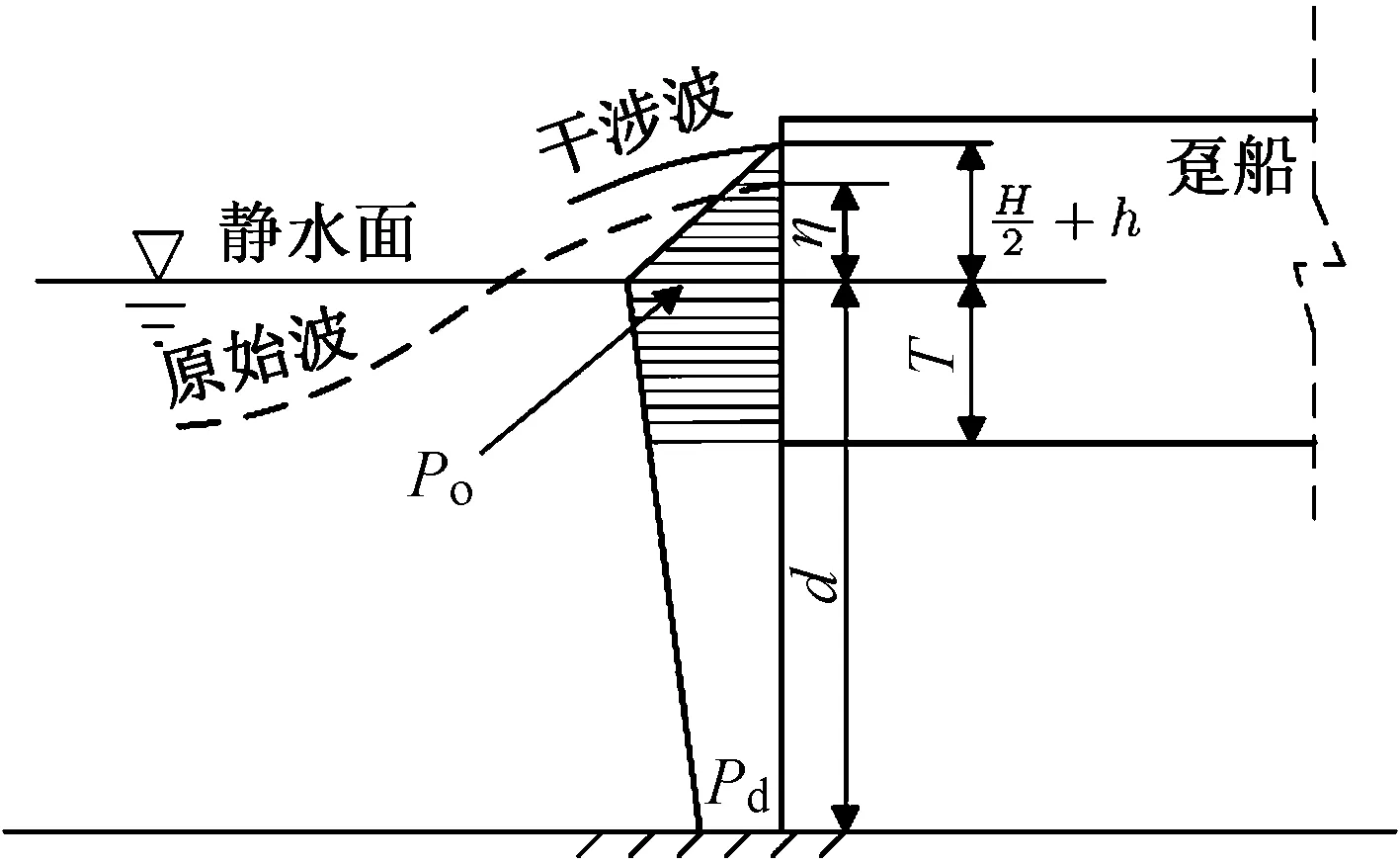
图11 波浪对趸船作用Fig.11 Wave impact on a barge

为了更接近于真实工况,建立桩基础吊箱结构三维模型,并根据真实吊箱下放入水施工工序,分别考虑吊箱位于静水面上部0.9m(等待入水)与吊箱入水0.6m两种垂向不同位置工况,分别计算吊箱结构受到的水平与垂向波浪力(见图12),由图可知,吊箱尚未入水时,水平波浪力最大可达240.5kN,而随着吊箱结构逐渐入水,水平荷载逐渐减小;垂向波浪荷载在吊箱结构尚未入水时即达到最大值(约为220kN),这表明在吊箱结构下水过程中需要格外关注入水前破碎波对吊箱的水平与垂向荷载。同时,对比二维与三维计算结果,发现水平力偏差相比较于垂向力较小,因而在实际工程中计算吊箱等三维结构水平力波浪时,可近似将二维计算结果通过宽度方向上拓展转化得到三维结果近似替代值,该方法能够显著降低三维模型计算耗时,且得到相对保守安全的结果。

图12 吊箱受到水平及垂向波浪力Fig.12 Horizontal and vertical wave forces

4.3 经济效益分析

通过研究发现,浅滩区吊箱结构受到的最大水平波浪荷载约为240.5kN,约为趸船模型估算结果177kN的1.4倍,因而仅仅根据规范结果设计吊箱等临时结构难以保证能够抵抗浅滩区破碎波作用,在实际施工过程中也多次发生浅滩区吊箱在破碎波水平砰击下发生明显形变及位移的问题,给施工安全与进度带来了诸多不利挑战。为克服浅滩区破碎波的影响,现场技术人员主要采用两种应对措施,一是加强吊箱结构强度,增强其抵抗破碎波荷载的能力,但改方案会增加临时结构投入成本,不利于大规模采用,仅适用于3～5m水深区间的桥梁基础施工,且吊箱结构尽可能标准化设计,利于周转重复利用;二是对于接岸极浅水区域,变更设计,提出采用墩柱盖梁结构替换原设计桩基础成塔结构,避免吊箱施工,为此项目技术人员发明了一种用于强涌浪浅滩区低墩盖梁悬挂支架,并形成了相应专利与工法,悬挂支架如图13所示,其以护筒为基础,外套大护筒,内外护筒间通过钢板焊接相连,大护筒上安装承重梁,横梁底部及四周设置挡浪板,形成干施工环境。相比较于原桩基础承台设计方案,变更后的一体化墩柱盖梁方案极大地节省了施工临时设施成本与工期,具体数据如表 1所示,变更后的一体化墩柱盖梁方案降低了波浪对施工的影响,提高了施工工效。

表1 浅滩区基础结构变更前后对比Table 1 Comparison before and after the change of the foundation in shoal area

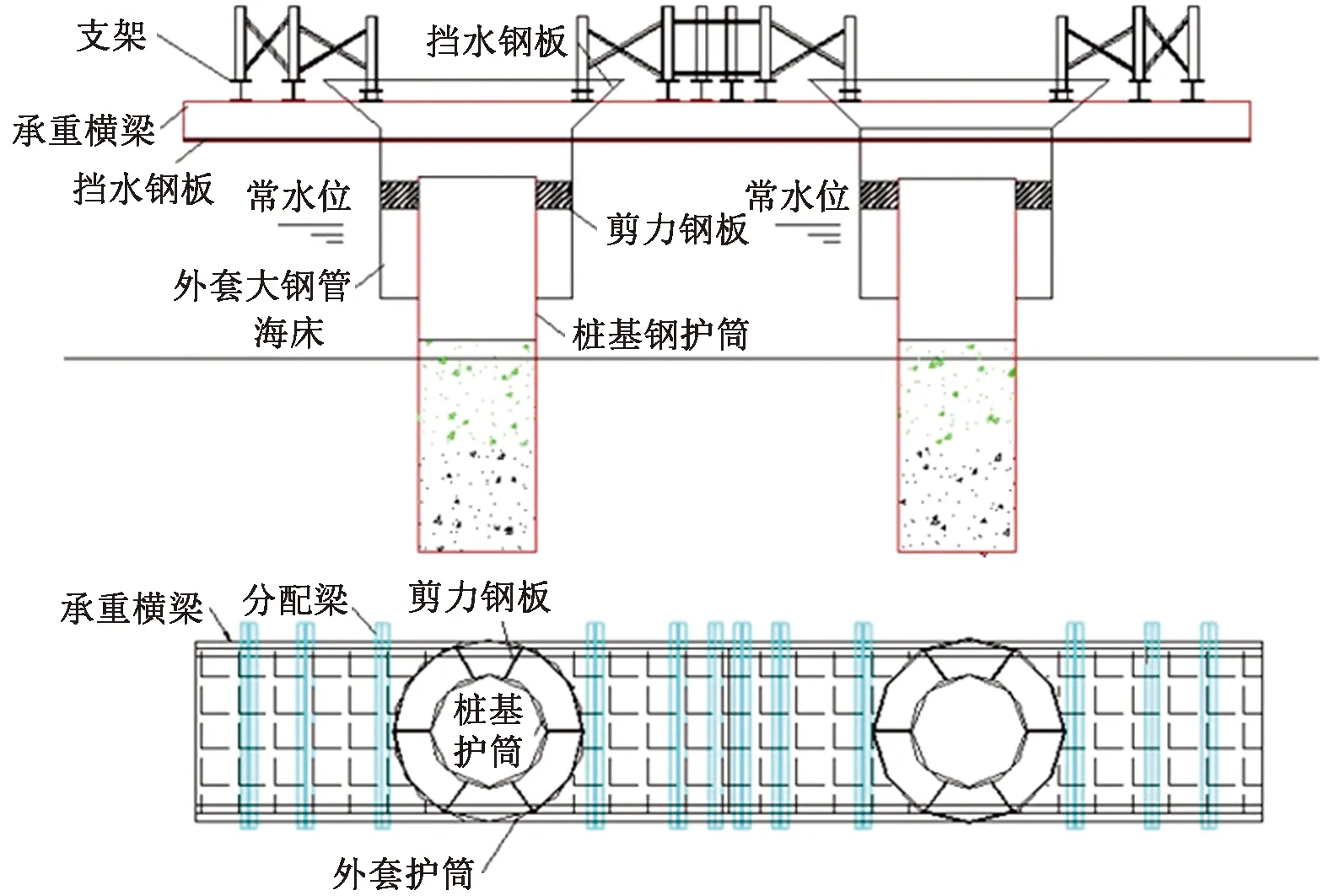
图13 浅滩区一体化墩柱盖梁悬挂支架Fig.13 Integrated pile beam suspension support in shoal area

5 结语

本文基于计算流体力学方法,采用聚焦波近似模拟波浪破碎,研究了浅滩区桥梁桩基础吊箱结构破碎波荷载。聚焦波达到最大波幅后会发生波浪翻卷、破碎等过程,相比较于通过设置斜坡改变地形模拟波浪破碎,该方法能够较为准确地在特定时间及位置模拟出破碎波,进而能够将桩基础吊箱结构放置在不同位置,研究波浪破碎过程中桩基础吊箱结构波浪荷载变化特性。经过研究发现,传统Morison公式低估了桩基础破碎波荷载,可根据具体问题乘以适当放大系数,本研究中工况放大系数取值为1.5;对于方形吊箱(承台),最大水平力发生在波浪达到最大波高后翻卷阶段,而非初始最大波高发生时,且整个作用过程极为短促,会出现一个瞬态的冲击;在吊箱结构尚未入水时垂向荷载即可达到最大值,建议实际施工过程中关注吊箱结构入水不同阶段时波浪荷载变化,以便合理设计钢吊箱入水施工工艺。针对接岸极浅水区域,将桩基础承台结构优化变更为一体化墩柱盖梁基础形式,并研发了一种强涌浪浅滩区低墩盖梁悬挂支架,降低了波浪对施工的影响,提高了工效。