新型吊脚墙支护二元基坑变形特征与地层适应性研究*

李隆平,周小涵,王林枫

(1.中铁大桥勘测设计院集团有限公司,湖北 武汉 430050;2.重庆大学,重庆 400045)

0 引言

城市地铁线路的建设与完善催生了越来越多多线换乘的情况,导致地铁车站越做越深,车站范围内地层上土下岩的情况越发普遍。在上土下岩地层中开展的基坑工程,本文称之为“二元基坑”。对于下卧岩层较好的二元基坑来说,为充分发挥下卧岩层的自稳与抵抗变形能力,普遍采用吊脚墙(桩)支护形式［1］。

关于吊脚墙支护下二元基坑的变形特征与变形规律的研究已较为丰富。孙连勇等［2］基于现场监测数据分析,提出吊脚桩支护下二元基坑变形时空演化规律。杨晓华［3］同样基于现场监测数据,分析了门式起重机移动荷载下土岩基坑变形特征。田海光［4］提出预应力锁脚锚杆能有效控制吊脚桩桩底水平位移,桩顶位移仅随开挖深度增加而增加。罗华标［5］通过对比吊脚墙加内支撑支护体系与一般连续墙加内支撑支护体系的差异,发现吊脚墙支护下基坑最大变形比一般地下连续墙稍大。二元基坑变形规律随地层差异变化较大。武军等［6］发现岩层弹性模量越大,对嵌入其中吊脚桩的约束作用越强。吴晓刚［7］总结了基坑变形与上部土层、土岩交界面、下部岩体的关系,提出围护结构侧移呈上部小、中下部大的“花瓶形”。刘红军等［8］通过数值分析,发现围护结构变形主要集中在土层部分,可有针对性地进行支护结构设计。

传统吊脚墙支护体系中,墙底需预留岩肩并采用预应力锚索锁脚,通过岩肩与锚索的嵌固作用约束墙底变形［5,9-10］。然而,吊脚墙预留岩肩会增加基坑占地面积,增加实施难度与挖方量,且当基岩强度较高时成槽困难。张群仲［11］提出在吊脚桩施工过程中,采用两侧边留一定长度岩石台背,中间基坑落底后逐步剥离台背的方法,是一种从有岩肩到无岩肩的过渡性措施。

为克服传统吊脚墙的局限,提出一种新型吊脚墙支护体系,即上部土层范围采用地下连续墙或者围护桩作为挡土构件,竖向设置多道支撑或预应力锚索,回筑阶段利用中板卡住挡土构件底部,形成稳定可靠的上部基坑支护体系;下部岩层范围采用垂直岩壁方案。并依托实际工程,采用有限差分软件FLAC3D 5.0建立数值计算模型,通过对比有无岩肩与预应力锚索锁脚和不同地层下基坑变形特征,探讨在类似基坑尺寸下,该新型吊脚墙支护体系的地层适应性问题,旨在推广这类新型吊脚墙支护形式在二元基坑中的实际应用。

1 二元基坑新型吊脚墙支护体系

1.1 工程概况

广州某地铁车站基坑全长276.2m,为地下4层岛式车站,采用明挖法施工,标准段宽47.1m,深32.981～33.634m。

车站场地地貌属于海陆交互相冲积平原地貌,为珠江河网交错的平原区,属河漫滩地,地形平坦开阔,河网密集,表层分布较多软土。自上而下依次为杂填土、素填土、淤泥质黏土、全风化砂岩、强风化砂岩、中风化砂岩和微风化砂岩。各地层分布及厚度如图 1所示。其中,全风化砂岩和强风化砂岩风化程度较高,可按土层考虑。站址区上覆土层厚度约9.0m,车站位于典型二元地层中。

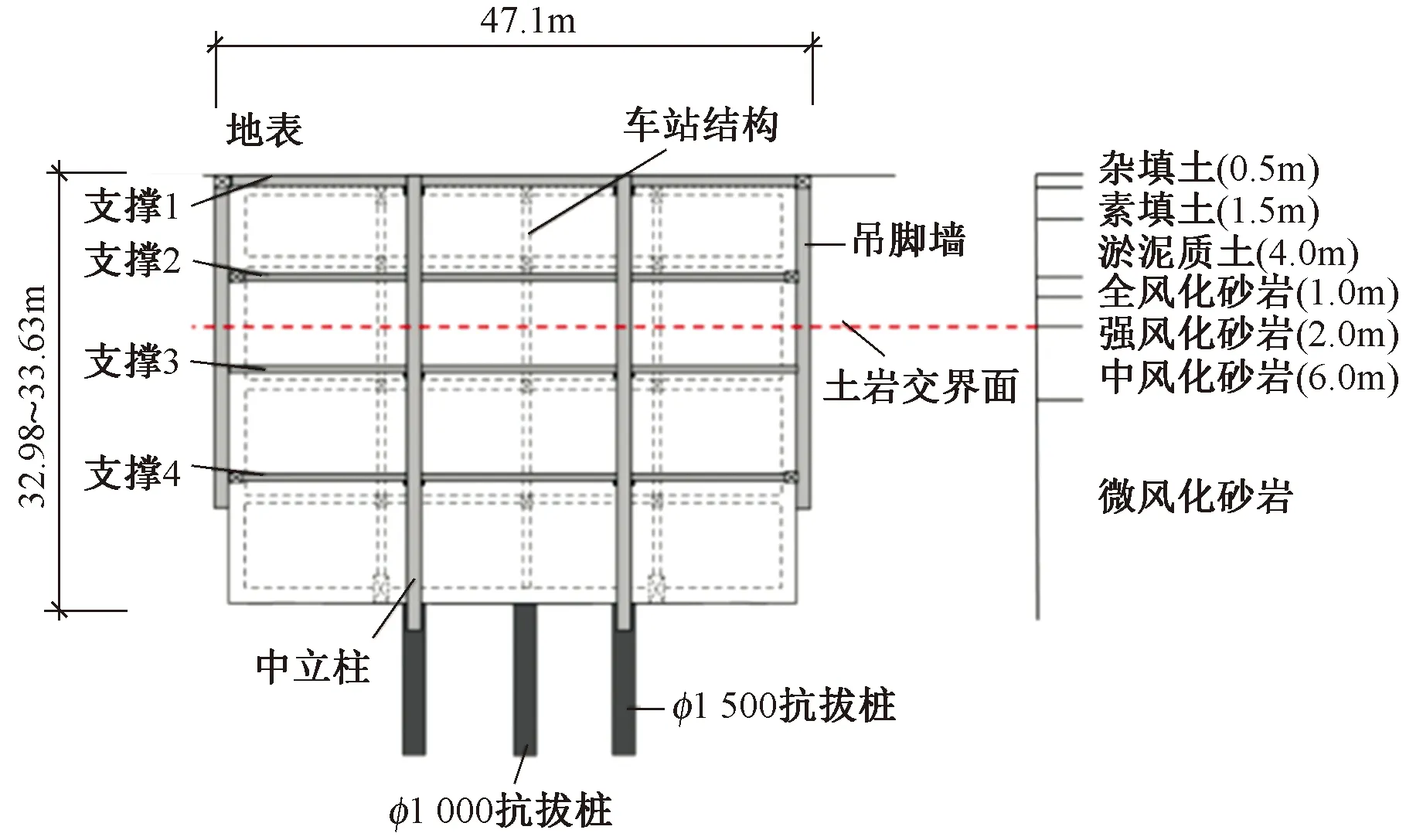
图1 广州某基坑断面支护形式Fig.1 Section support form of a foundation excavation in Guangzhou

车站北侧为赤岗涌,与下部地层间存在一定的水力联系,对基坑开挖及支护影响较大。场地内地下水水位总体埋藏相对均较浅,水位埋深2.2～3.1m,水位年变化幅度为1.5～2.5m。

1.2 新型吊脚墙支护体系

传统二元基坑吊脚墙支护结构,底部需要预留一部分岩肩。本文提出的新型吊脚墙支护体系是指在二元基坑支护设计中,在上部土层范围采用地下连续墙或者围护桩作为挡土构件,挡土构件间竖向设置多道支撑或预应力锚索,回筑阶段利用中板卡住挡土构件底部,形成稳定可靠的上部基坑支护体系,无须依靠墙底嵌岩和预应力锚索锁脚来解决支护体系安全问题,在下部岩层范围采用垂直岩壁方案。与传统预留岩肩吊脚墙支护结构相比,该新型吊脚墙支护体系的优势为：①节省基坑占地面积;②节省基坑挖方量;③节省投资;④在初期未外放预留岩肩的条件下,后期改嵌底墙为该新型吊脚墙无限制条件。

具体结构形式及组成如图 1所示。采用地下连续墙+4道内支撑作为围护结构,连续墙厚800mm,深24.6m,墙底位于地下3层中板底以下1.5m左右,4道内支撑均采用混凝土支撑,深度分别为0.5,6.5,13.8m和21.0m,其中上3道支撑尺寸为800mm×1 000mm,最下道支撑尺寸为1 000mm×1 300mm。设有格构柱,格构柱底部施作φ1 500mm钢筋混凝土立柱桩,基底采用φ1 000mm钢筋混凝土抗拔桩抗浮。

2 数值计算方案

2.1 计算模型

为阐明该无岩肩无预应力锁脚锚索的新型吊脚墙支护形式下二元基坑变形特征,依托该工程,采用有限差分软件FLAC3D 5.0分别建立传统带岩肩吊脚墙支护体系与新型吊脚墙支护体系数值计算模型并求解。通常,长条形基坑可采用二维平面应变模型进行分析［12-13］,故本文中同样建立二维计算模型,模型宽度取为1.0m。考虑消除模型边界条件,基坑宽度方向需要向外扩展3～5倍基坑深度,基坑下卧坚硬岩层,故模型深度方向取为60.0m,最终确定模型尺寸为249.0m×1.0m×60.0m(长×宽×高)。

为探讨一般规律,将复杂地层简化成1层土层和1层岩层,其中,土层为粉质黏土,岩层为砂岩,如图 2a和图 2b所示。其中,图 2b为按照实际工程建立的计算模型,图 2a为在此基础上,增加岩肩与锁脚锚索,岩肩尺寸为宽1.0m,高2.0m,预应力锚索的设置参考文献［14］,并转化成单位宽度模型对应参数,最终确定的锚索长12.0m,直径2φ25mm,倾角15 °,高度设置在岩肩高度中部,施加160kN预应力。需要注意的是,为反映支护结构可能产生的塑性变形甚至破坏,水平支撑采用实体单元模拟,并赋予弹塑性本构模型［15］。

2.2 计算参数

数值计算中,本构关系和参数的确定对计算结果非常关键。莫尔-库伦本构模型具有参数少且容易获得、概念简单而又能反映土的应力应变特征,是关于基坑的数值模拟中常见的本构模型［16-17］。因此,本模拟中采取莫尔-库伦本构模型作为土层以及岩层的本构模型,地层物理力学参数如表1所示。

表1 地层物理力学参数Table 1 Physical and mechanical parameters of formation

为反映支护结构由于刚度不足而产生的塑性破坏,模拟中吊脚墙和水平支撑均采用莫尔-库伦本构模型,格构柱、立柱桩和抗拔桩采用弹性本构,具体参数如见表2所示。

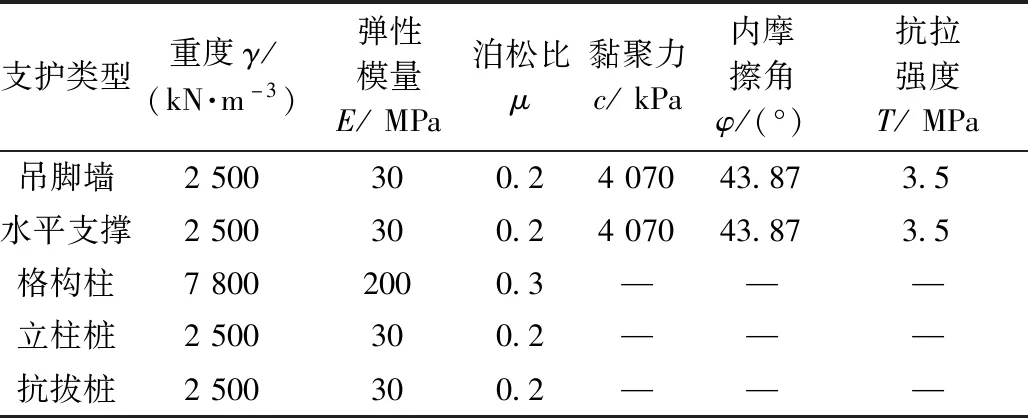
表2 支护结构参数Table 2 Supporting structure parameters

在吊脚墙和地层之间设置接触面以反映支护结构与地层的相互作用,通过试算,最终确定接触面参数如表3所示。

表3 接触面参数Table 3 Contact surface parameters

2.3 计算工况

当前,采用吊脚墙支护的二元基坑土层均不厚,挡岩段深度均较深,以确保基坑稳定,同时,下卧岩层性质也较好。为探讨不同地层条件下二元基坑变形特征与新型吊脚墙变形控制效果,进而总结地层适应性,保持基坑尺寸不变,选取土岩交界面深度和下卧岩层质量两个因素,设计数值计算工况如表4所示。其中,1～6组下卧岩层为实际微风化砂岩,而土岩交界面深度不同,7～12组土岩交界面深度为9.0m,而下卧岩层质量不同,其中,7组、10组下卧岩层均为实际微风化砂岩,8组、11组为场区中风化砂岩,9组、12组岩层性质介于场区中风化砂岩与强风化砂岩之间,分别定义这3类岩体为良好、一般和较差,其具体参数取值如表5所示。土岩交界面深度为9.0m而下卧岩层为微风化砂岩的情况与实际场地条件更为接近。

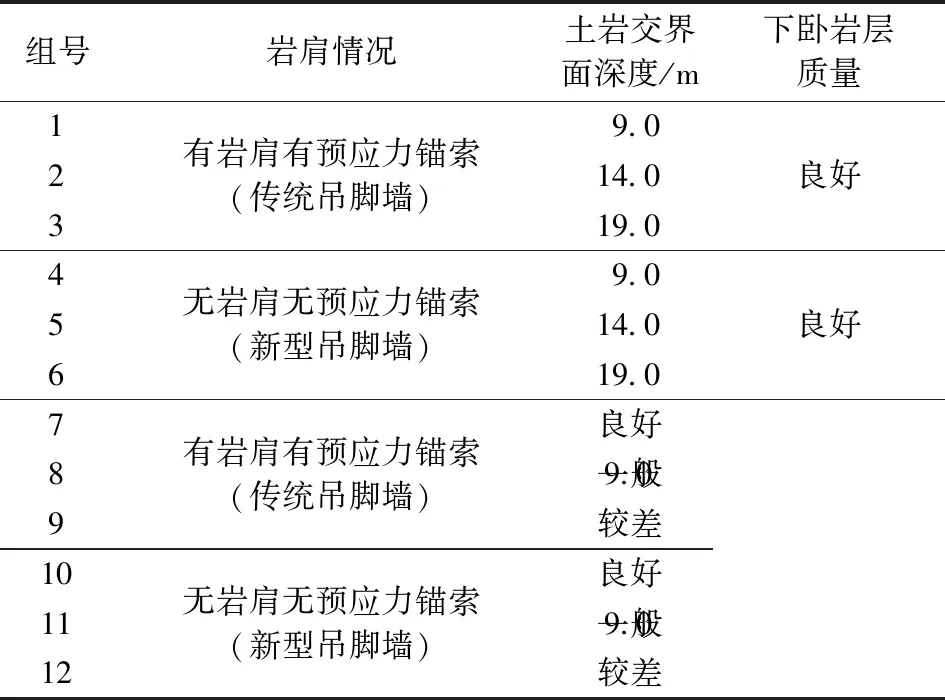
表4 考虑土岩交界面深度的数值计算工况Table 4 Numerical calculation condition considering the depth of soil rock interface

表5 下卧岩层物理力学参数Table 5 Physical and mechanical parameters of underlying rock stratum

强调指出,在中风化砂岩以及比中风化砂岩更软的岩层中,实际工程中不采用吊脚墙支护方案,本文只是为了考察地层适应性而刻意弱化下卧岩层,对地层适应性做初步尝试性探讨,为进一步研究探路。

2.4 计算过程

数值计算过程遵循如表6所示计算步骤。

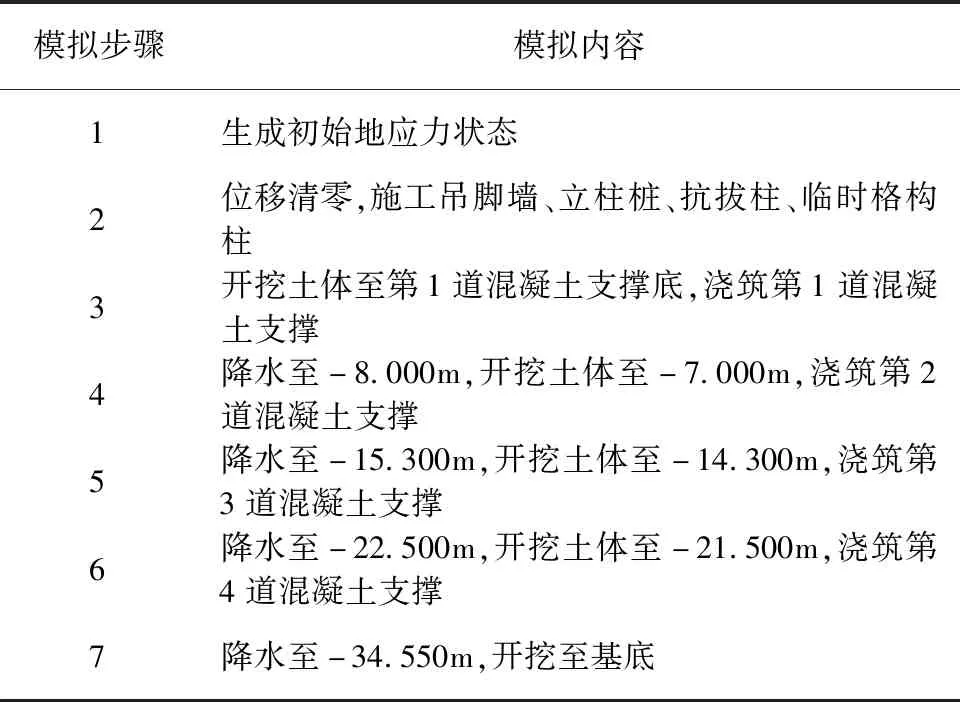
表6 数值计算步骤Table 6 Numerical calculation steps

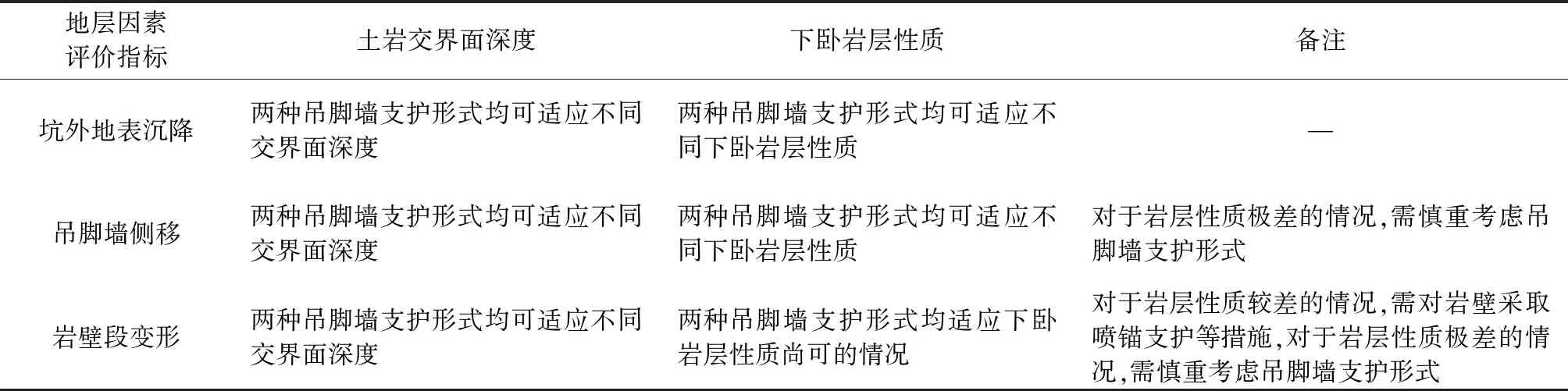
表7 吊脚墙支护体系地层适应性评价Table 7 Stratum adaptability evaluation of support system of suspended toe wall

需要注意的是,为准确反映基坑开挖卸载引起的基坑变形,在基坑开挖阶段,采用地层的回弹模量代替弹性模量。毕港等［18］提出对于基坑工程而言,地层的回弹模量可以取为弹性模量的5倍,因此,本文数值模拟同样取地层回弹模量为弹性模量的5倍参与计算。

3 计算结果验证

车站施工全过程中,对车站周围地表沉降、围护结构变形、围护结构内力、地下水位等进行了详细监测,选取典型位置处坑外地表沉降、围护结构侧移监测数据,并与土岩交界面深度为9.0m而下卧岩层为微风化砂岩的工况作对比,用于验证数值计算结果的准确性,如图 3所示。

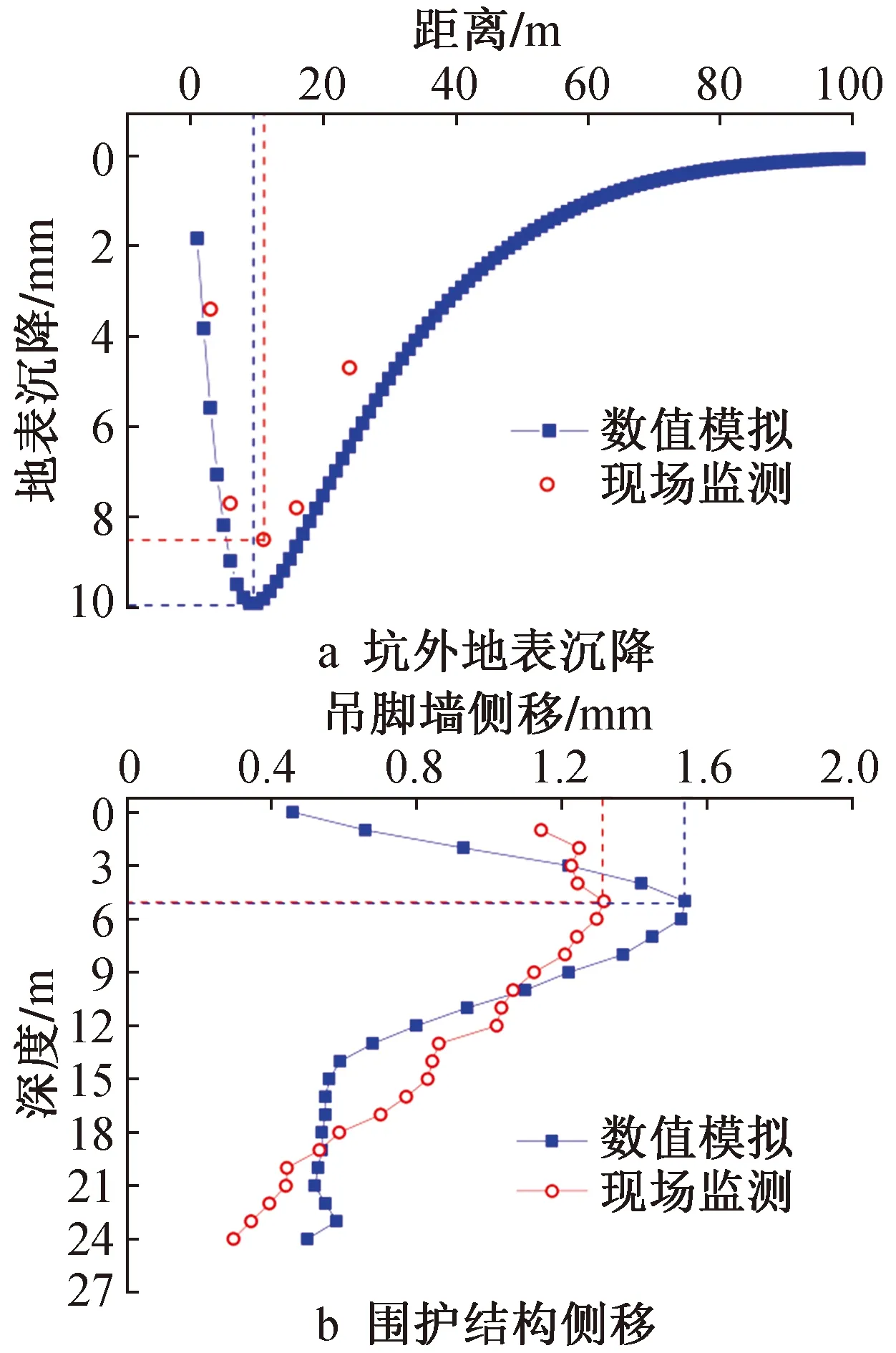
图3 数值计算结果与现场监测对比Fig.3 Comparison of numerical results with field monitoring

可以看到,总体上,数值模拟与现场监测数据对应良好,表明数值计算较为准确,可用于进一步研究。数值模拟得到的坑外最大地表沉降与围护结构最大侧移均稍大于监测结果,原因在于模拟中对地层作出了一定简化,将土层简化为1层粉质黏土,而实际上土层非均质,且存在一定风化层,其变形小于纯土。此外,数值模拟得到的坑外最大地表沉降位置与围护结构最大侧移位置与实际监测结果较为一致。

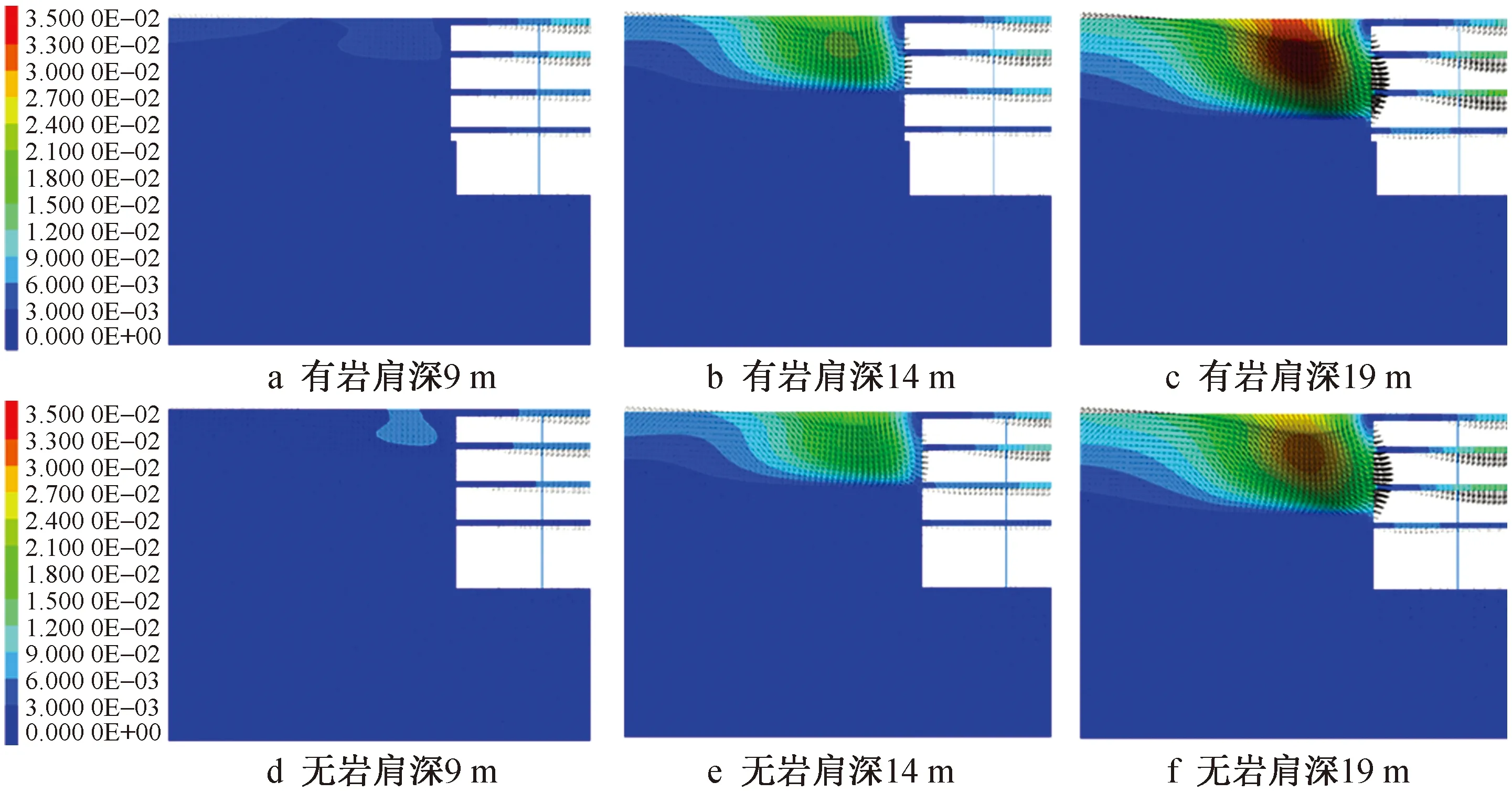
图4 不同土岩交界面深度下基坑总位移云图Fig.4 Cloud chart of total displacement of foundation excavation at different soil rock interface depth

4 不同地层条件下二元基坑变形特征

4.1 基坑总位移

不同土岩交界面深度下开挖完成后基坑总位移如图 4所示。为方便对比,各工况下变形梯度均一致。与传统有岩肩有预应力锚索吊脚墙相比,新型吊脚墙支护结构总体上说支护效果相差不大。随土岩交界面深度增大,土体位移显著增大,当土岩交界面深度为9.0,14.0,19.0m时,土体最大位移分别为9.0,24.0,35.0mm,同时,吊脚墙与支撑变形相应增大。岩壁段变形受交界面深度影响不显著。总体上,对于下部岩层良好的二元基坑,无论土岩交界面深度如何,基坑的变形模式均表现为上部土体向坑内滑动,挤压吊脚墙向坑内发生“胀肚形”变形,下部岩壁段变形很小,能保持稳定。

不同下卧岩层质量下开挖完成后基坑总位移如图5所示。总体上,有无岩肩对基坑的变形模式影响不大。基坑变形主要位于上部土层中。随着下卧岩层质量的弱化,基坑与围护结构变形均逐渐增大,当下卧岩层质量良好、一般、较差时,基坑最大位移分别为9.0,18.0mm和25.0mm左右,均位于距离基坑约0.3倍土层深度至1.5倍土层深度范围内,同时,地表变形区范围逐渐扩大。岩层质量弱化降低了其抵抗变形的能力,使得吊脚墙下部挡岩段变形增大,进而在协调变形作用下弱化了上部挡土段支挡能力,导致土层段变形增大。此外还可以发现,当岩层质量较差时,由于岩壁段承载能力与抵抗变形能力的弱化,吊脚墙与水平支撑体系会发生较大沉降变形,且岩壁段产生一定向基坑内的挤出变形。说明在较深的基坑,很差的岩层内不适合做吊脚墙结构。

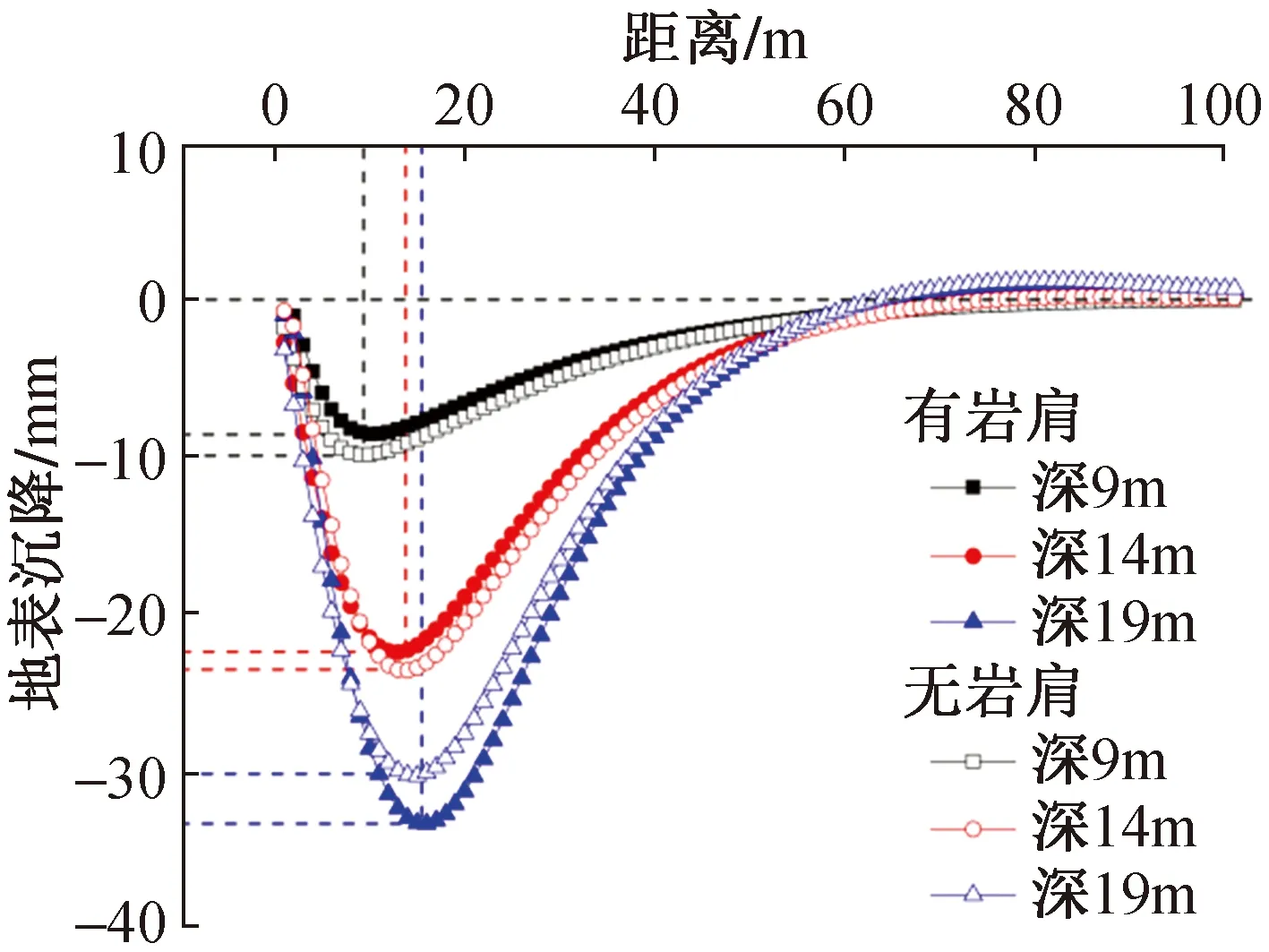
图6 不同土岩交界面深度下坑外地表沉降曲线Fig.6 External surface settlement curve of excavation under different soil rock interface depth

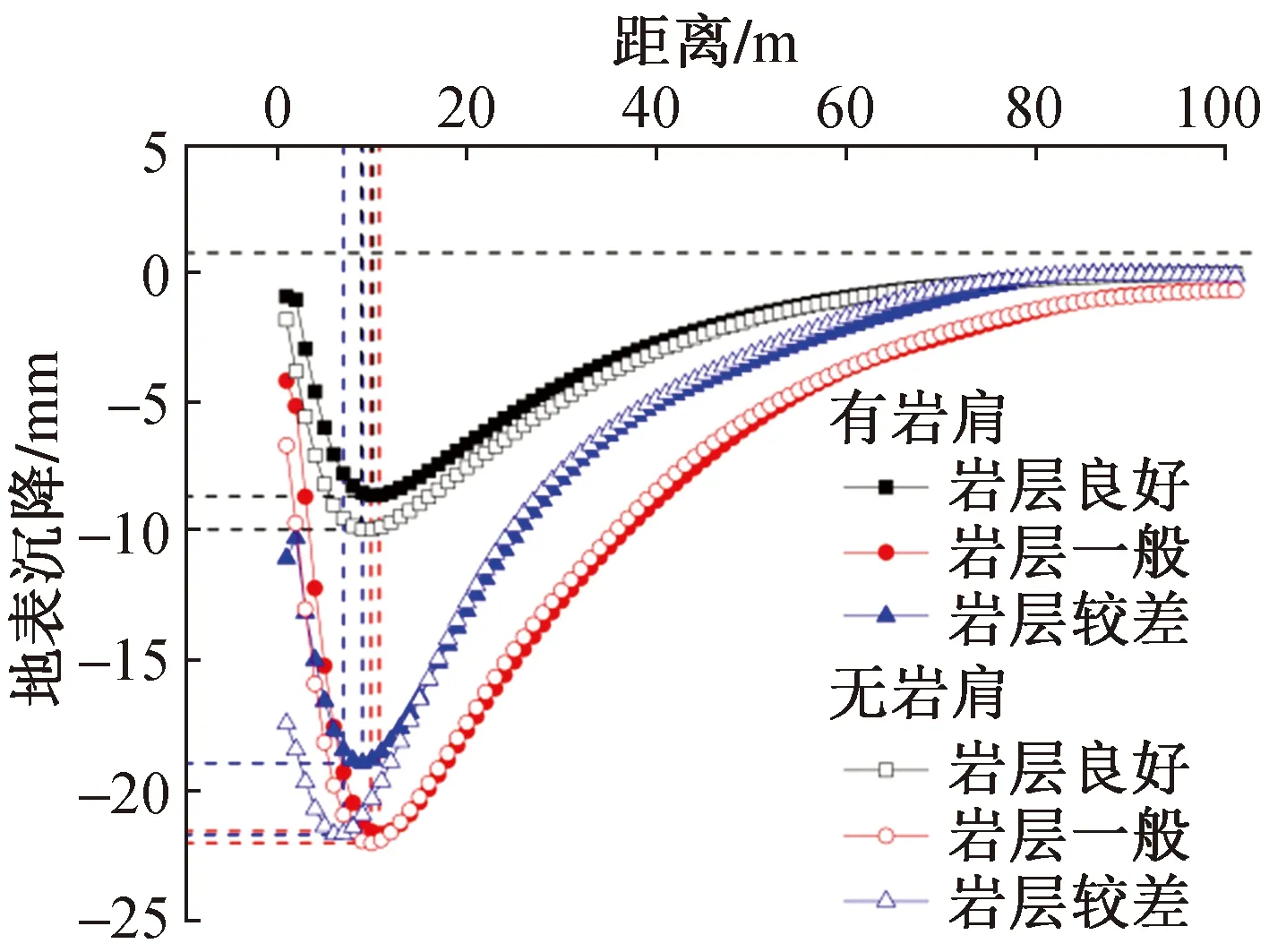
图7 不同下卧岩层质量下坑外地表沉降曲线Fig.7 External surface settlement curve of excavation under different underlying rock mass

4.2 坑外地表沉降

不同土岩交界面深度下开挖完成后坑外地表沉降如图 6所示。可见,不同土岩交界面深度下,采用无岩肩的新型吊脚墙支护结构产生的坑外地表沉降与传统带岩肩吊脚墙均基本相同,均呈典型“凹槽形”曲线,说明岩肩对坑外地表沉降而言影响很小,取消岩肩合理可行。随着土岩交界面深度增大,坑外地表沉降逐渐增大,交界面深度在9.0,14.0,19.0m时,坑外最大地表沉降分别为10,23,32mm,且最大沉降位置逐渐向坑外移动。

不同下卧岩层质量下开挖完成后坑外地表沉降如图 7所示。同样地,地表沉降呈典型“凹槽形”曲线。但与图 6相比存在以下不同,随着岩层质量弱化,地表沉降先迅速增大后甚至有所减小,原因与前述基坑总位移部分类似,当岩层质量较好时,弱化岩层可引起基坑变形较大的变化,而当岩层质量较差时,岩层质量弱化对基坑变形影响很小,甚至由于支护结构协调变形能力反而减小。此外,从最大沉降量和位置上看,下卧岩层质量的改变对地表沉降的影响较土岩交界面深度更小,说明下卧岩层性质不是坑外地表沉降的主要影响因素。与土岩交界面相同,不同下卧岩层下,有无岩肩与预应力锚索对地表沉降的影响不大,说明岩肩与预应力锚索的锁脚作用有限,推广无岩肩无预应力锚索的新型吊脚墙支护体系可行。

4.3 吊脚墙侧移

不同土岩交界面深度下开挖完成后吊脚墙侧移曲线如图8所示。总体上,不同深度下吊脚墙侧移均呈现中间大,两端小的“胀肚”形变形模式,且变形主要发生在上部土层中。新型吊脚墙的变形情况与传统吊脚墙相比相差不大,最大侧移量相差在2mm以内,且最大侧移深度相同,由于取消岩肩后无论从施工成本还是进度需求上均存在明显优势,可考虑取消岩肩。随土岩交界面深度增大,吊脚墙最大侧移值不断增大,当交界面深9.0,14.0m和19.0m时,吊脚墙最大侧移分别为1.6,7.2mm和16.2mm,最大侧移位置逐渐下移,最大侧移位置分别在5.0,9.0m和11.0m附近,均处在土层深度内,说明吊脚墙最大变形均位于上部土层中。对于上覆土层较浅的情况,可考虑优化支护结构刚度以降低成本,对于上覆土层较深的情况,当前的支护体系仍然具有较好的支护效果,说明了该新型吊脚墙支护体系的适用性。

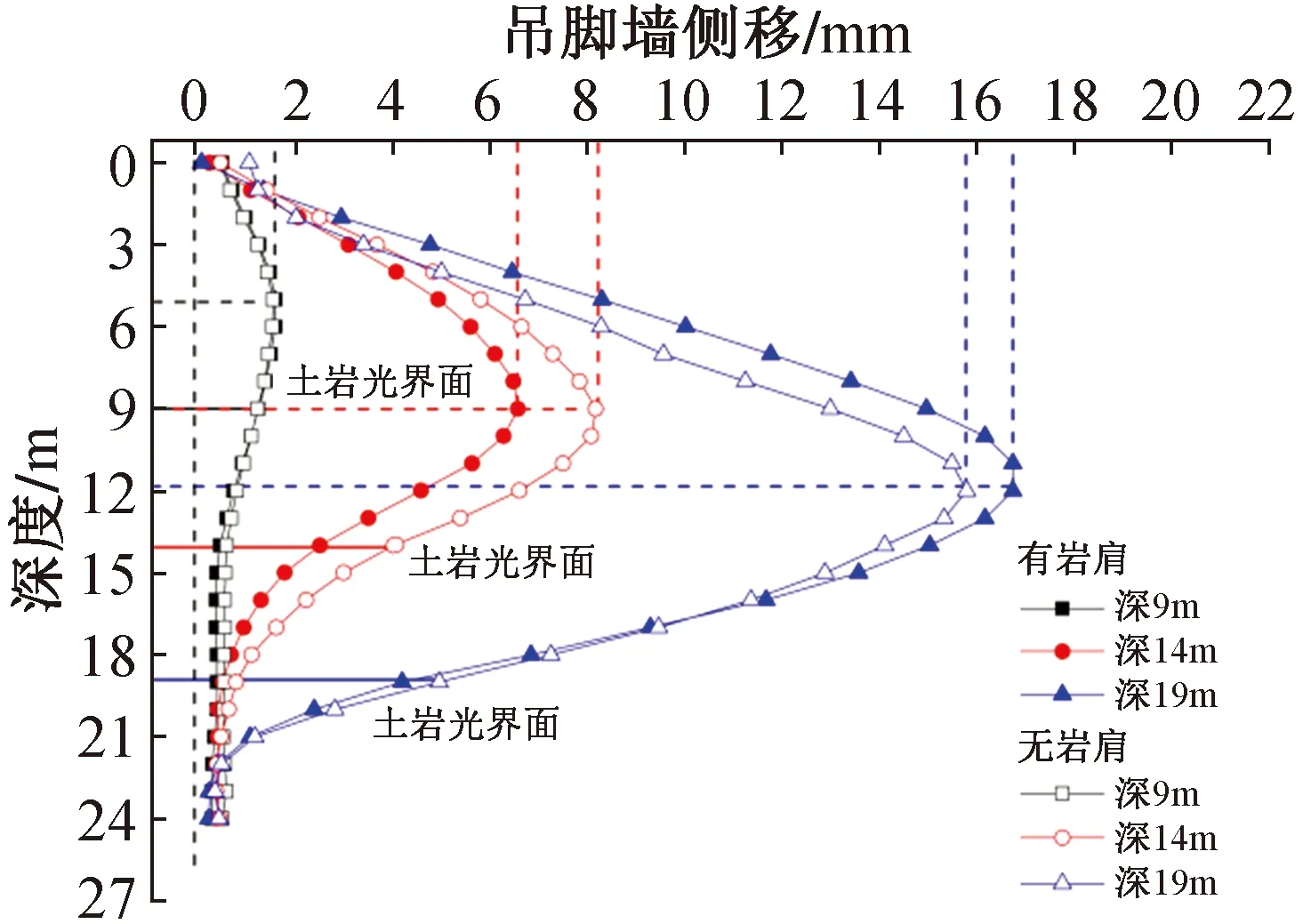
图8 不同土岩交界面深度下吊脚墙侧移曲线Fig.8 Lateral displacement curve of suspended foot wall under different soil rock interface depth

不同下卧岩层质量下开挖完成后吊脚墙侧移曲线如图 9所示。可以看到,吊脚墙的最大侧移值随基坑下卧岩层质量弱化逐渐增大。但与图 8规律不同的是,不同下卧岩层情况下,基坑吊脚墙的变形模式不同。当基坑下卧岩层质量良好时,吊脚墙呈典型“胀肚”形变形模式,且变形主要集中在上部土层段;当基坑下卧岩层质量一般时,由于岩层承载能力与抵抗变形能力的降低,吊脚墙下半部分变形较大,几乎与中部最大位移值接近;当基坑下卧岩层质量较差时,吊脚墙变形呈“折线形”变形模式,吊脚墙底部向坑内发生较大变形。当下卧岩层质量良好或一般时,采用新型吊脚墙支护体系能起到与传统吊脚墙几乎相同的变形约束效果,而当下卧岩层质量较差时,无论是新型吊脚墙还是传统吊脚墙,其变形都随着地层变形发生协调,导致局部变形较大,且无岩肩吊脚墙变形稍大,但总体上均未超限,说明了新型吊脚墙支护体系在不同下卧岩层质量中均能适应。

4.4 岩壁段变形

图 10为不同土岩交界面深度下岩壁段变形特征,各工况下变形梯度均保持一致。总体上,各工况下岩壁段的变形模式较相似,在卸荷作用下,岩壁段产生向基坑内部的变形,不随有无岩肩和土岩交界面深度改变表现出较大差异。相比于上部土层段,岩壁段变形处于较低水平,均在0.6mm以内,可以保持稳定。

图 11为不同下卧岩层质量下岩壁段变形特征,各工况下变形梯度均保持一致。与图 10相比,下卧岩层性质不同时,岩壁段变形差异较为明显,当下卧岩层性质较好时,有无岩肩下岩壁段均基本不发生变形,当下卧岩层性质一般时,有无岩肩下岩壁段均向外发生约7mm的变形,而当下卧岩层性质进一步弱化,岩壁段开始产生大变形,侧上方岩体有从岩壁段滑动挤出的趋势,传统吊脚墙由于岩肩和预应力锁脚锚索的作用,岩壁段变形较小,约在19mm左右,而新型吊脚墙支护结构对岩壁段变形约束作用较弱,岩壁段最大变形为24mm,且变形范围明显较大。可得出结论,下卧岩层质量对岩壁段变形影响较大,而岩肩对岩壁段变形影响较小,对于下卧层质量较好的情况,采用新型吊脚墙支护体系可获得与传统吊脚墙相同的支护效果,而对于下卧层质量较差的情况,传统吊脚墙支护体系效果稍好,但不明显,对于此类岩层,在采用吊脚墙进行支护的同时,需在岩壁段采取喷锚支护等方法,优化岩壁段受力状态,控制岩壁段变形。

5 地层适应性评价

基于本文数值模拟结果,可进一步总结新型吊脚墙支护体系与传统吊脚墙支护体系的地层适应性,如表 7所示。

综上,对于基坑尺寸与本文依托工程类似的土岩基坑,选取土岩交界面深度与下卧岩层质量作为地层适应性指标,无论是新型吊脚墙支护体系还是传统吊脚墙支护体系,均具有较好的地层适应性,尤其是土岩交界面深度,在下卧岩层质量较好、吊脚墙支护体系设计合理、施工规范的前提下,几乎不影响支护效果,而当下卧岩层质量较差时,新型吊脚墙支护体系适应性略低于传统带岩肩吊脚墙,当下卧岩层质量极差时,需慎重考虑吊脚墙支护形式,此时应采用传统嵌岩围护结构。

6 结语

依托实际工程,采用有限差分软件FLAC3D5.0建立数值计算模型,通过对比有无岩肩和预应力锁脚锚索,以及不同地层条件下基坑变形特征,探讨在类似基坑尺寸下,无岩肩新型吊脚墙支护体系在不同地层条件下的变形特征,评价该体系的地层适应性,得到以下结论。

1)采用无岩肩新型吊脚墙支护体系和传统预留岩肩吊脚墙支护体系,在不同地层条件下变形特征与支护效果差异很小,取消岩肩与预应力锁脚锚索合理可行。

2)当下卧岩层质量较好时,随土岩交界面深度增大,土层段变形显著增大,下部岩壁段变形很小,能保持稳定,坑外地表沉降逐渐增大,最大沉降位置逐渐外移,吊脚墙最大侧移值不断增大,最大侧移位置逐渐下移。

3)随下卧岩层质量弱化,基坑最大位移和坑外地表沉降先增大后影响不大,吊脚墙最大侧移逐渐增大,变形特征由“胀肚”形变形模式向“折线形”变形模式转变,吊脚墙底部变形较大,岩壁段变形增大,有向外滑移趋势。

4)无岩肩新型吊脚墙支护体系和传统预留岩肩吊脚墙支护体系均具有较好的地层适应性,其中在不同土岩交界面深度下均适用,在下卧岩层质量偏差时,需对岩壁段进行喷锚支护,或考虑采用传统嵌岩围护结构。