土石混合料填方地基压实质量快速检测方法研究*
余 雄,于同生,王 涛,李 杨
(1.中建五局第三建设有限公司,湖南 长沙 410000;2.同济大学土木工程学院,上海 200092)
0 引言
随着我国近年来基础建设的快速发展,适合直接进行工程建设的良好工程用地越来越少,因此出现了大量建设于山区的工程。对于此类工程,场平方案大多采用就地取材、削山填谷的方式。就地开挖填方的方式不仅节约材料和运输成本,且挖山得到的填料工程性质良好,非常适用于山区的地基平整工作。该方法具有诸多优点,但还需要对填方过程中的压实质量进行严格把控。规范中建议采用灌水(砂)法进行压实度检测,该方法适用于所有填料的压实质量检测,但随着填料粒径的不同需要开挖不同大小的试坑,试坑直径至少为填料最大粒径的5倍,深度为试坑直径的1.2倍。对于公路填方路基来说,填料一般为砂土,试坑直径约取10cm,深度取12cm左右就可以取得较好的检测效果。而对于山区填方工程,填料为石头和土的混合材料,尽管在填方前对大直径石块进行了破碎,但仍存在大量大直径石块(5~15cm),此时采用灌水(砂)法检测的试坑尺寸直径至少为45cm,深度50cm,经试验测试,包含开挖试坑及烘烤土样时间,单点检测时长约在50min。由于填方过程需要对压实质量进行逐层检测,且需要满足一定的检测密度,此时采用灌水(砂)法检测的效率将难以满足实际工程需要,亟需寻找一种针对土石混合料填方地基的压实质量快速检测方法。
针对上述问题,国内外学者开展了大量关于土石混合料压实质量快速检测方法的研究。核子湿度密度仪法是一种快速压实质量检测方法,JTG E60—2008《公路路基路面现场测试规程》中规定可以将其应用于路基的压实质量检测,赖余斌[1]对其在土石混合料填方地基压实质量检测中的适用性进行研究,结果表明在含石量较低时,核子密度仪的测试误差相对较小,但当含石量较高时,其测试误差将无法满足工程需要。有学者提出采用沉降率测试法检验填土压实质量[2-3],尽管原理层面沉降率(沉降深度/虚铺厚度)与压实系数可互相转化计算,但笔者在实际应用过程中发现诸多不便之处。首先虚铺厚度在实际工程中难以确定,受粒料不均影响,虚铺厚度很难处于统一标高,该参数的测量误差直接导致后期沉降率计算参数不准确;其次填方工程通常为多区域同时开展,实际施工过程中很难做到每个施工区域分派1名检测人员进行实时高程监测,因此该方法同样不适用于土石混合料的压实质量检测。Ji等[4]提出采用CT扫描方法结合离散元建模的方法确定土石混合料最大干密度和压实系数的方法,尽管该方法在实验室中有较高的计算精度,但考虑到CT扫描技术应用于施工现场的局限性,同样难以应用于工程实践中。
因此,土石混合料压实质量快速检测方法,应同时具备准确性和实用性两大特征。JT/T 1127—2017 《公路路基填筑工程连续压实控制系统技术条件》规定可通过在试验段建立振动压实机械参数(压实过程中的加速度监测数据)与压实系数的相关关系式,在实际施工过程中通过压实机械参数间接推算压实质量的方法。类似地,采用便携式落锤弯沉仪(portable falling weight deflectormete,PFWD)同样可以获取基于加速度监测数据计算得到的动态变形模量值,进而建立与压实系数间的相关性关系式,实现间接测试压实质量的目标,经测试该方法在公路路基压实质量检测过程中同样获得了较好的检测效果[5-6]。
由前所述,PFWD方法在路基压实质量检测领域具备较好的适用性,但公路路基填料大多均匀性较好。但对于土石混合填料,存在变异性强、填料粒径大、含水率变化范围大等特点,其适用性还有待探究。因此,针对这一问题,本文结合工程实测数据,开展了采用PFWD方法间接评价土石混合料压实质量的有效性研究。
1 基于PFWD的压实质量检测方法
采用PFWD方法进行压实质量检测,其简要过程如下:首先通过预实验阶段的灌水法与动态变形模量测试试验,建立密度或压实度与动态变形模量的相关关系;当二者的相关性达到一定程度时(一般建立线性关系),即可在此基础上通过动态变形模量的测试推算土石混合料的压实质量。同时,为了保证PFWD测试结果的稳定性与准确性,需对同一测点进行至少3次重复试验,当结果相对稳定时,认定此次测试结果有效。
本文所使用的动态变形模量测试仪其检测深度范围为检测面地表下30~50cm。该设备的测试原理是通过对承压板作用1个确定的冲击荷载,通过记录承压板位移(加速度)信息,在假设土体和承压板协同变形的条件下,根据弹性力学理论,计算得到土体动态变形模量的过程[7-9],其计算公式如下:
(1)
式中:μ为泊松比,取0.21;d为荷载板直径(mm);σ为平均压应力;s为测试弯沉值,单位精确至0.01mm。
2 试验方案
土石混合填料最大的特征就是具有不均匀性,即不同位置的填料其含石量、含水率和最大粒径都存在较强的不确定性。对于工程实践而言,即使有意控制含石量与含水率,但填料性质仍具有极强的不确定性。以本工程所在的试验场区为例,尽管所要求的含石量为40%,但实际测得的含石量在20%~70%,含水率也与最佳含水率存在一定偏差[8]。尽管PFWD方法被证明于公路路基压实质量检测领域具备较好的效果,但其填料与土石混合料有极大差别。公路路基填料相对均匀,且含水率控制较好,简言之对于待检测土体,其变量主要为压实度的不同;而对于土石混合料来说,同一场地范围内填料具备极强变异性,最大粒径、含石量、含水率和压实度均不确定,此时通过PFWD方法间接计算压实系数是否仍然有效则需要进一步探究。
从理论层面分析,当填料均匀,且含石量、含水率均大致相同,仅压实度有所差别时,PFWD法检测得到的动态变形模量值与填料压实系数一定具备极强的相关性,公路路基试验的检测结果也从侧面验证了这一结论。对于土石混合料而言,若要实现相同的检测效果,则需分别建立多个含石量、多个含水率情况下的相关关系式,再由此进行间接压实质量评价。然而对实际工程来说,若已知晓待测点位的含石量和含水率,其压实度检测工作已完成大部分工作量,此时再采用PFWD方法进行压实质量评价不具备工程意义。
因此,为使研究结果具备更强的工程应用价值,本文将填料岩土种类作为唯一控制变量,即研究填料均挖自同一山包区域,但并未对填料含石量、含水率进行分类,这对实际工程检测而言是切实可行的。整个试验均结合实际工程项目开展,选择某一填方区域,跟随检测单位人员同步进行压实质量检测。具体测试方法如下:对待测点位首先进行PFWD法试验,得到该点位的动态变形模量测试数据;随后由检测单位在相同位置处进行灌水法密度试验,并获取其检测湿密度、含水率和计算干密度数据。整个试验过程共跟踪测试填方深度为8m,填方层数16层的填方区,获得同一填料类型的检测数据579组。
3 试验结果分析
3.1 Evd与密度相关性分析
现有文献中建立压实系数与动态变形模量的参数关系大多是针对细粒土,部分研究结论显示动态变形模量与压实系数或干密度之间存在较好的线性关系。然而针对土石混合料来说,基于本文的试验数据发现,动态变形模量与压实质量参数之间并不存在一定的线性关系或非线性关系,这也与张向文等[9]的研究结论相似。动态变形模量与湿密度、含水率和干密度关系的散点图如图1~3所示,由图可知动态变形模量与3个参量相关性均很差,最大相关系数仅为0.22左右,显然无法建立相关性方程并应用于实际工程检测当中。
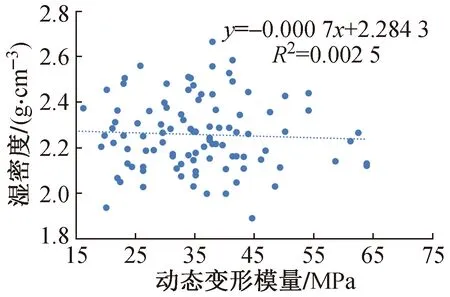
图1 动态变形模量与湿密度关系散点图Fig.1 Scatter plot of dynamic deformation modulus versus wet density

图2 动态变形模量与含水率关系散点图Fig.2 Scatter plot of dynamic deformation modulus versus moisture content

图3 动态变形模量与干密度关系散点图Fig.3 Scatter plot of dynamic deformation modulus versus dry density
PFWD方法在公路路基压实质量检测过程中动态变形模量与压实系数的相关系数均在0.7以上,对比土石混合料的相关性较差的结果,分析其原因可能如下:由于土石混合料的变异性特征,不同点位的含石量、含水率和压实度均存在较大的不确定性,仅仅依靠动态变形模量一个参数难以建立与多个变量的相关关系。以动态变形模量与湿密度的相关性分析为例,处于低压实质量、高含水率状态与高压实质量、低含水率状态可能具备相同的湿密度,但其压缩性质显然相差极大,即动态变形模量不同。因此,对于土石混合料填方工程而言,很难通过动态变形模量间接评价地基土压实质量。
3.2 PFWD位移时程曲线与密度相关性分析
由3.1节分析可知,仅通过动态变形模量无法建立与压实参数的相关性模型。不同测点采用PFWD方法测试过程中典型的位移时程曲线如图4所示。可以看出两个测点计算得到的动态变形模量值相等,但位移时程曲线有所差别,相应的湿密度分别是2.18g/cm3和2.0g/cm3。根据式(1)中动态变形模量计算公式可知,Evd计算仅体现了位移时程曲线的最大值。事实上对于两个密度存在差异的点,即使Evd计算值相同,其位移时程曲线也会有所差异,表明位移时程曲线中可能包含更多关于压实质量的信息,即有可能基于此建立与压实质量参数的相关性模型。

图4 相同Evd不同湿密度时程曲线对比Fig.4 Comparison of time course curves for different wet densities for the same Evd
位移时程曲线记录了PFWD测试过程中111个时刻的位移值,常规的数据处理手段难以直接基于此建立曲线与湿密度、含水率和干密度的相关性模型。然而结合时下较为火热的人工智能技术则可以较为简单地实现这一目标。
BP神经网络是一种多层前馈神经网络,基于其良好的非线性映射建模能力已在多行业得到了广泛应用,并受益于近年来计算机算力和人工智能技术的快速发展,可以极其简便地将其应用于多参数的建模过程中[10-11]。
首先以位移时程曲线与湿密度的相关模型建立为例,研究二者之间的相关关系。输入参数为位移时程曲线上按顺序排列的位移值(每个点均取3次测试结果的平均值),输出参数分别为湿密度、含水率和干密度。总数据量共有579组,以其中500组作为训练数据,79组作为测试数据,需要说明的是,每次选择的500组训练数据和79组测试数据均为随机选择,通过多次重复测试的结果作为评判神经网络模型优劣的标准。
隐含层节点数量为12个时,79个测试点实测湿密度与基于BP神经网络模型计算湿密度的对比散点图如图5所示。由图5可以看出,即使是包含多组土石混合料粒径、含石量和含水率的条件下,整体而言基于BP神经网络模型所构建的湿密度计算模型误差较小。湿密度覆盖区间从1.9~2.3g/cm3,与工程实际相符。图6为BP神经网络计算湿密度误差从大到小排列的分析图,最大计算误差为9%,平均计算误差为2.4%,误差小于8%的数据量为77个,占总数据量的97.5%,误差小于6%的数据个数为74个,占总数据量的93.7%,误差小于4%的数据个数为66个,占总数据量的83.5%。且通过数据分析发现,误差较大的点位主要集中在低密度区和高密度区,即处于端点位置。考虑到灌水法进行密度检测过程中同样存在一定的人为误差,该误差范围基本可以被工程实践所接受。

图5 实测湿密度与BP神经网络模型计算湿密度散点图Fig.5 Scatter plot of measured wet density and BP neural network model calculated wet density
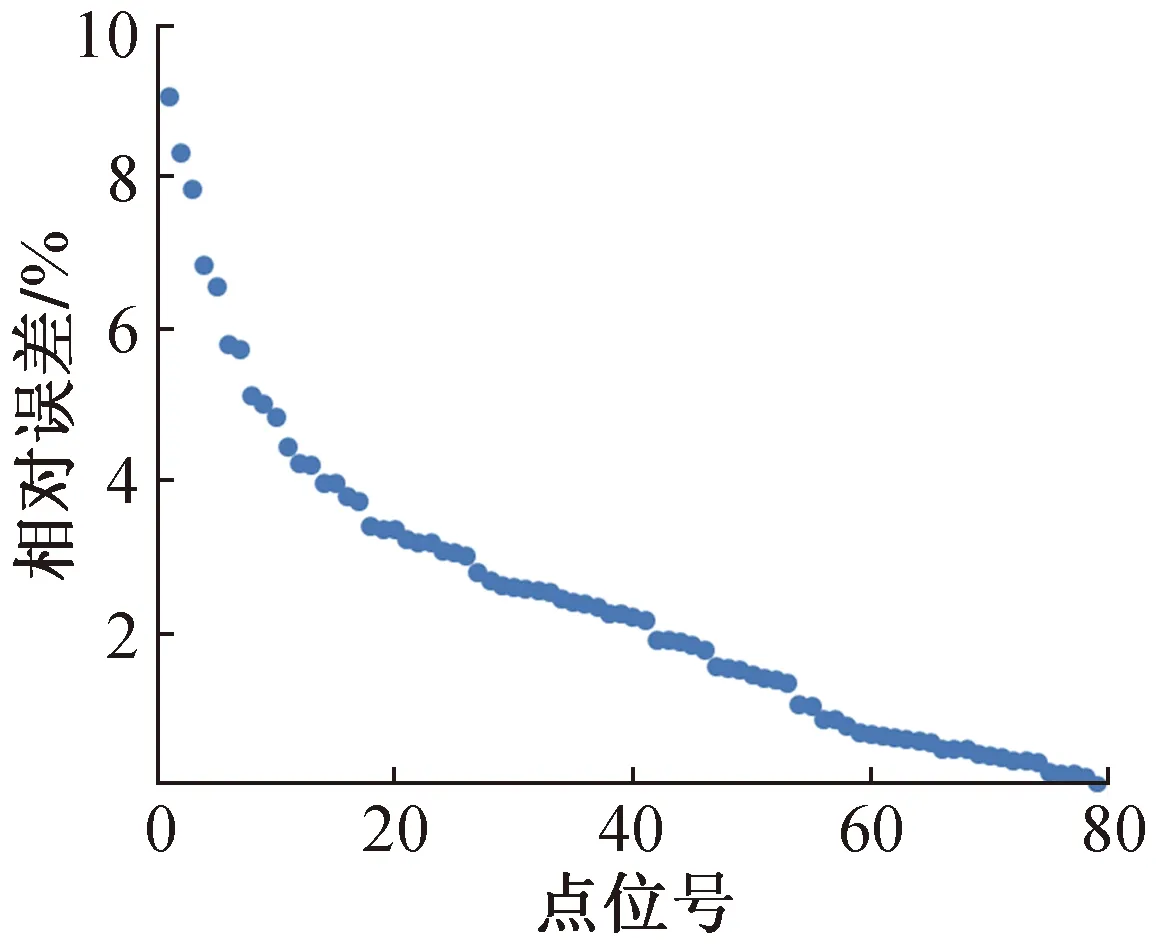
图6 BP神经网络计算湿密度误差分析Fig.7 Error analysis of wet density calculation by BP neural network
尽管根据BP神经网络计算湿密度的效果较好,但通过多次重复测试发现,并非每次测试结果均可以达到的理想效果。如图7所示为相同神经网络参数情况下的计算效果,由图7可以看出,在实测湿密度较大时,BP神经网络的计算误差较大,且误差小于4%的数据个数仅为25个,占总测试数据量的68.4%,相较于之前的83.5%差距较大。多次重复测试结果表明,最终误差率平均值在2.9%左右,误差最大值的平均值在12%左右,误差小于6%的点位数占总点位数据的90%左右,上述分析结果表明该方法具备一定的可行性,但其鲁棒性还有待提高。
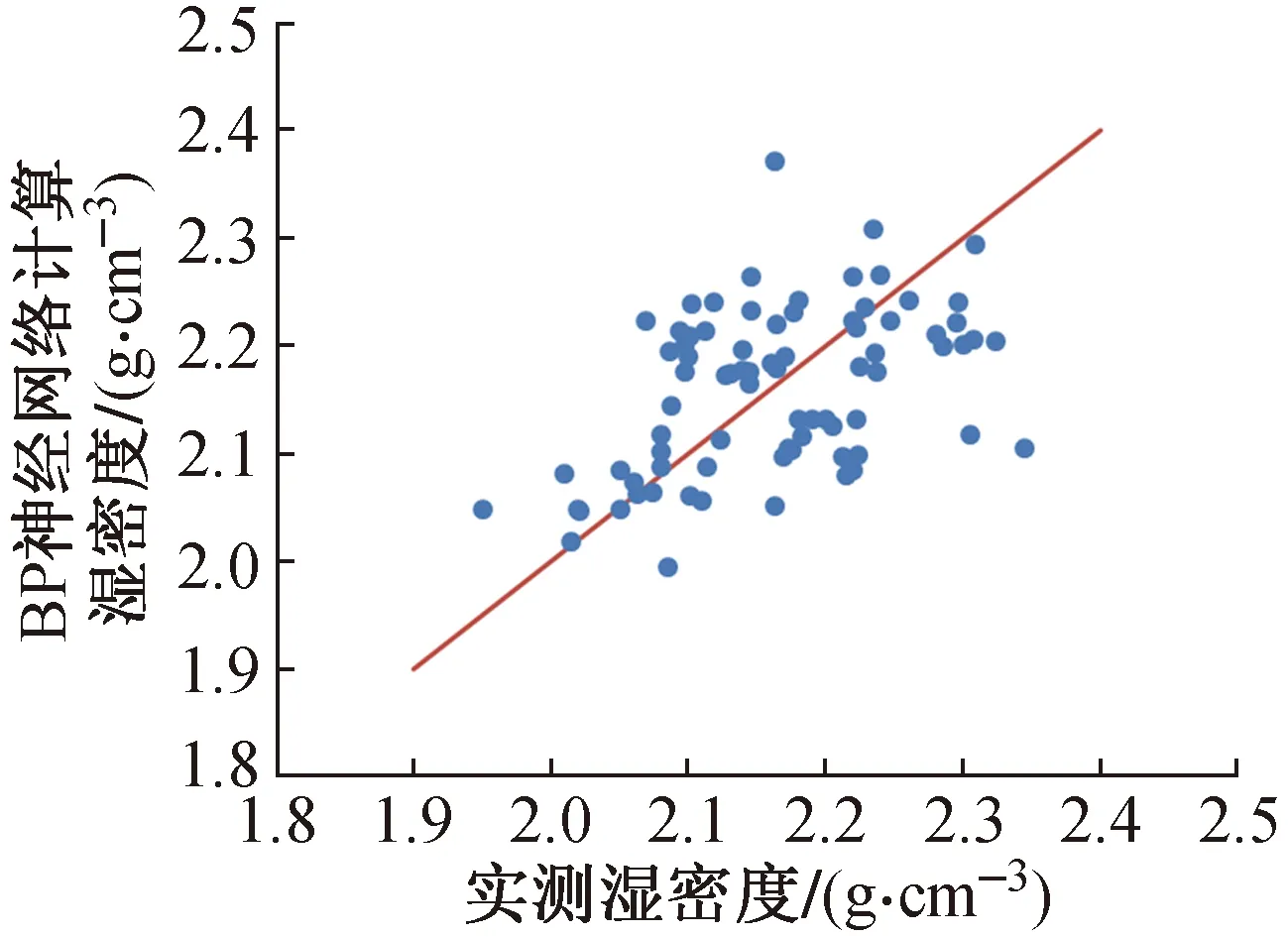
图7 实测湿密度与BP神经网络模型计算湿密度散点图Fig.7 Scatter plot of measured wet density and BP neural network model calculated wet density
由于BP神经网络在使用过程中每次权值和阈值均为随机生成,不同的权值、阈值参数会对最终的计算结果产生一定影响,因此会影响其计算结果的鲁棒性。而遗传算法是一种寻优算法,其基本原理是通过不断交叉、选择和变异等操作寻找规定条件所设置的最优解[12-13]。因此,可以将遗传算法与神经网络模型相结合,通过遗传算法的寻优特性寻找BP神经网络计算误差最小的权值和阈值[12-13],由于该方法已有较成熟的应用,具体实现过程不在此赘述。
基于遗传算法优化后BP神经网络进行湿密度计算的结果如图8所示,对比之前未经改进的神经网络模型最佳预测效果可以看出,二者之间并无明显差异,且从整体误差来看,平均误差为2.5%,误差最大值为7.7%,误差小于6%的点位数占比为96%,误差小于4%点位数占比为82%,二者差异性同样很小(见图9)。但不同点在于,基于遗传算法改进的BP神经网络模型总能得到类似的计算结果,相较于一般的神经网络模型,计算结果的鲁棒性得到了极大提升。

图8 改进BP神经网络计算湿密度与实测湿密度散点图Fig.8 Scatter plot of calculated wet density and measured wet density by improved BP neural network
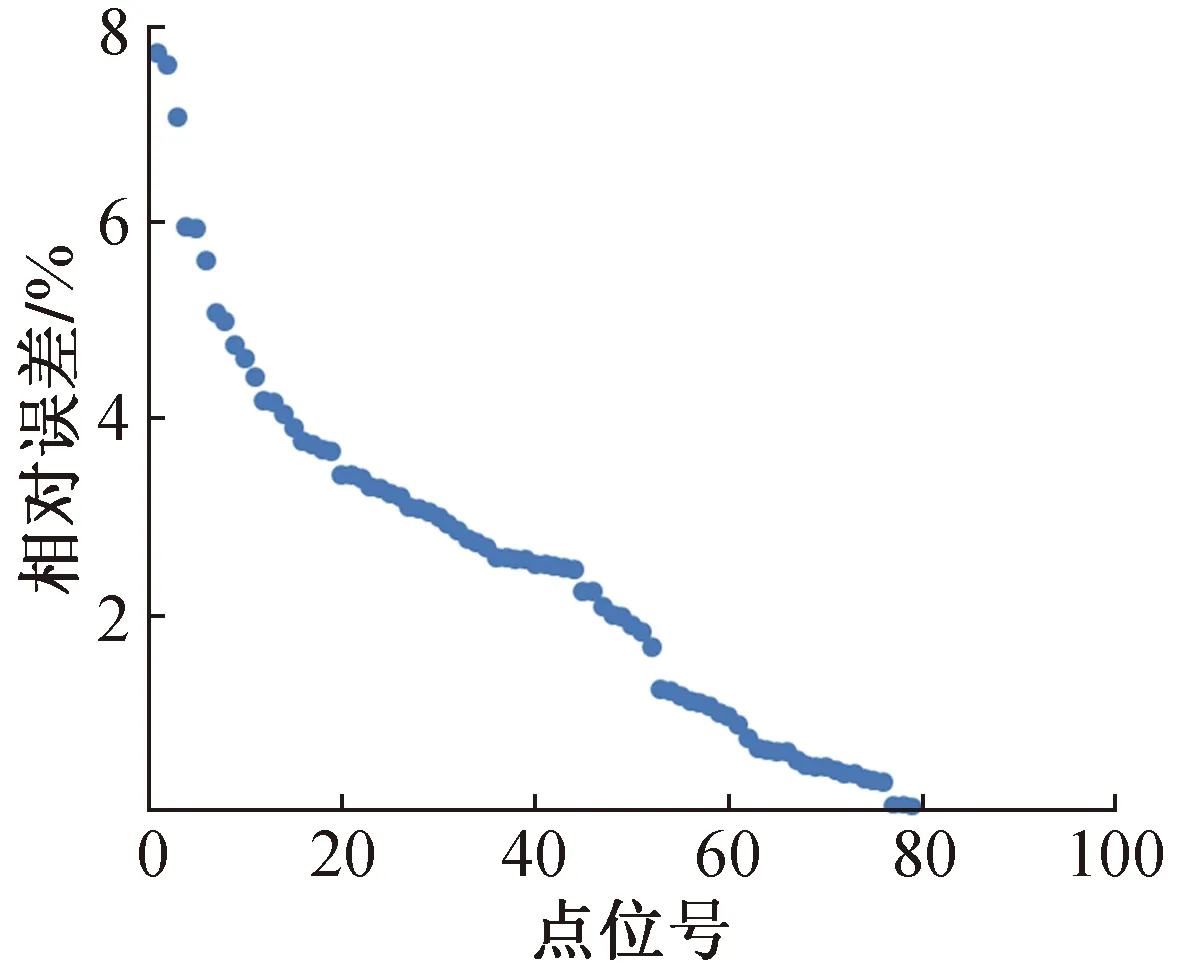
图9 改进BP神经网络模型误差分析Fig.9 Error analysis diagram of improved BP neural network model
基于遗传算法优化后的改进BP神经网络模型可以建立PFWD过程中位移时程曲线与湿密度的相关性模型,且计算平均误差仅为3%左右。按照同样的过程,对位移时程曲线与干密度、含水率间的相关性模型进行评析。基于位移时程曲线和改进BP神经网络计算干密度、含水率与实测值的散点图和误差分析如图10,11所示。由图10可知,位移时程曲线与干密度间存在一定的相关性,但相较于湿密度的相关性关系来说较差。其最大误差为13%左右,平均误差为4.2%,均大于湿密度计算过程中的误差。由图11可以看出,基于改进BP神经网络计算得到的含水率与实测含水率间相关性较差,基本上无法通过位移时程曲线推算填料含水率。
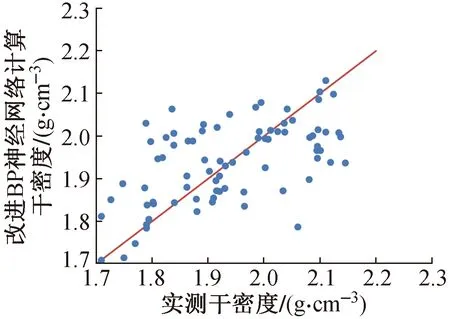
图10 改进BP神经网络计算干密度与实测干密度散点图Fig.10 Scatter plot of dry density calculated by improved BP neural network versus measured dry density
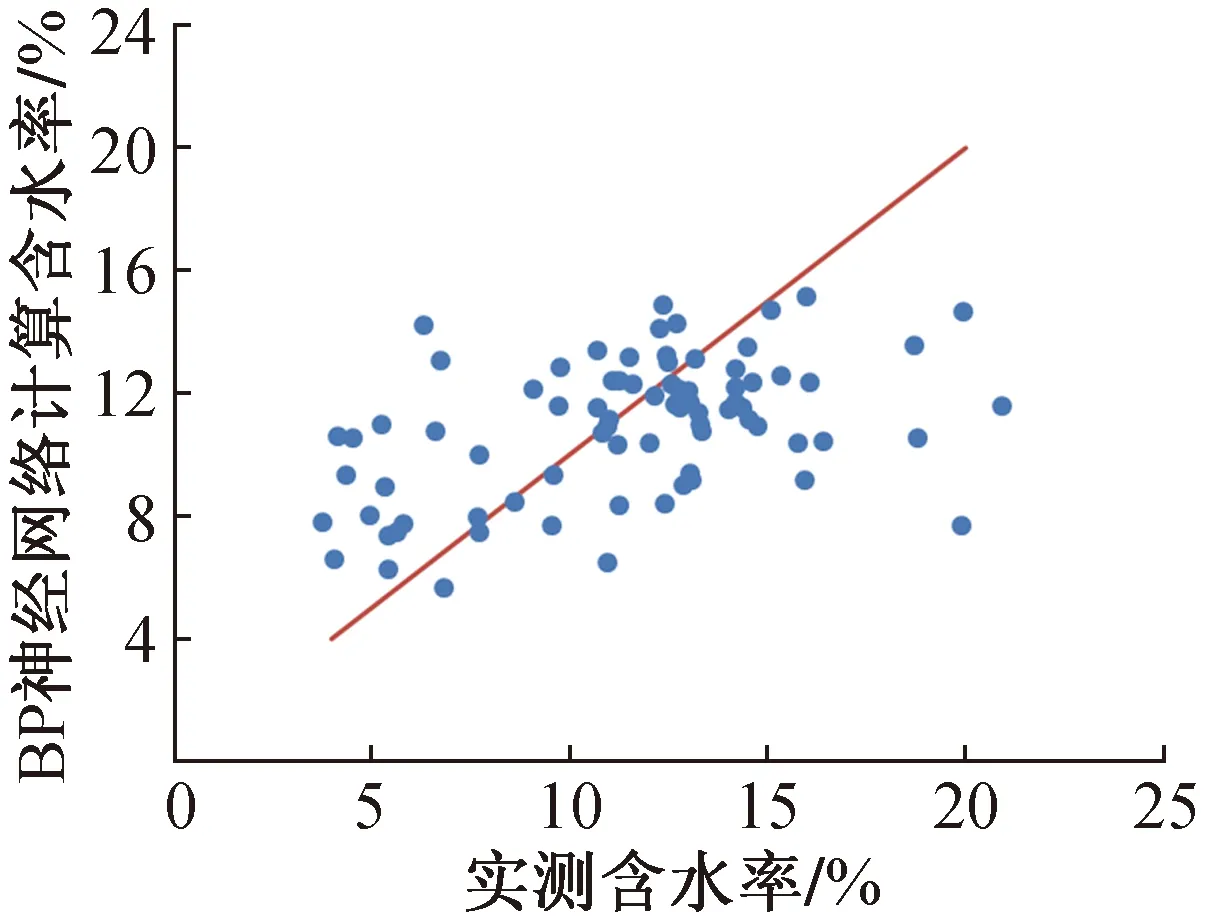
图11 改进BP神经网络计算含水率与实测含水率散点图Fig.11 Scatter plot of calculated water content and measured water content by improved BP neural network
3.3 水分仪测试含水率可行性分析
由前述分析可知,基于便携式落锤弯沉仪测试过程中得到的位移时程曲线,结合遗传算法改进的BP神经网络模型,可以建立得到时程曲线与湿密度较好的相关性模型,相比之下,时程曲线与干密度、含水率之间的相关性模型误差则较大。而地基压实质量评价需要干密度计算压实系数,在已知湿密度的情况下,还需要获取测点的含水率信息。
含水率的常规测试方法为烘干法,主要测试原理为通过高温烘干受测试土体中的水分,利用烘干前后的质量差计算水分质量,进而计算填料含水率,然而该方法对于土石混合料的检测效率却难以适应于工程实践。为了保证检测速度,本文尝试一种更为快捷准确的测试方法,即水分仪测试法。
水分仪是一种应用于农林灌溉领域的测试设备,其基本测试原理如下,通过触探钢针测试一定土体范围内的电阻率,又根据电阻率与含水率的相关关系,换算得到土体的含水率值。需要说明的是,仪器显示的含水率是体积含水率,而通常岩土工程领域所用的含水率为质量含水率,二者还需要进行换算,其基本换算公式如下:
ω=θω/(ρ-θω)
(2)
式中:ω为质量含水率;ρ为待测土体测试状态下的湿密度;θω为待测土体的体积含水率,即水分仪显示数据。土壤传感器主要测试构件为3根钢针,钢针需要与土体充分接触。由于设备研发适用领域主要针对农业,测试土体为松软土体,而课题所需测试土体为经压实后土体,很难直接插入压实后的土体中,且土石混合料中存在部分石料,直接插入极可能对钢针造成损坏。通过不断摸索实践,最终梳理得到以下测试流程,可以实现对土石混合料中细粒料成分含水率的测试。
1)第1步 取一固定容积的容器,可以是水杯等器皿,挖取测点位置处的细粒土放置于水杯中,并将水杯内的土体轻轻用手压实至较紧密状态。
2)第2步 称量容器+土的质量,减去容器质量得到其内土体质量,再由事先知晓的容器体积计算得到杯中土体湿密度。
3)第3步 将水分仪钢针插入器皿内的土体中,读取测试数据,重复3~5次,取平均值,根据式(2)计算得到土体的质量含水率。
几个测点重复测试过程中体积含水率测试结果如表1所示,可以看出,水分仪测试效果具有良好的稳定性,从低含水率到高含水率的重复多次试验结果可以看出,数据始终保持在某个狭窄区间范围内,表明基于该仪器的测试结果是有效并且可信的。

表1 水分仪测试效果Table 1 Results of moisture meter tests
由于采用水分仪测试含水率会影响测点完整性,影响后续进行灌水法试验结果,因此设置以下两个试验验证采用水分仪进行土石混合料含水率测试的有效性。
1)试验1 从工程现场随机挖取部分土石混合料,筛分得到粒径2cm以下土样,采用加水或烘干的方式获得不同含水率土样,随后分别采用前述水分仪测试法和烘干法测试相同对照组土样的含水率。
2)试验2 在进行灌水法试验时,将土石混合料根据粒径筛分为不同粒径组,并测试每个粒径组的质量和含水率,并逐一采用烘干法测试含水率,由此可以得到细粒土和土石混合料的总含水率。总含水率计算公式如下:
(3)
式中:ωz为填料的总含水率;Ni为第i个粒径组的质量百分数;ωi为第i个粒径组的含水率。
土体水分仪测试含水率与烘干法测试含水率的散点图如图12所示。由图中数据可以看出,二者尽管不是完全相等,但存在极强的线性关系,相关系数均在0.95以上,表明可通过水分仪测试细粒料含水率。细粒料含水率与混合料整体含水率的散点图及相关性曲线如图13所示,二者相关系数可以达到0.95以上,也就是可以通过测试细粒料含水率推算得到混合料整体含水率。由此,通过预实验阶段的相关性分析,就可以直接建立水分仪测试含水率与土石混合填料整体含水率的相关关系式,进而实现快速测试含水率的目标。

图12 水分仪含水率测试结果与烘干法结果对比Fig.12 Moisture meter moisture content test results compared to drying method results
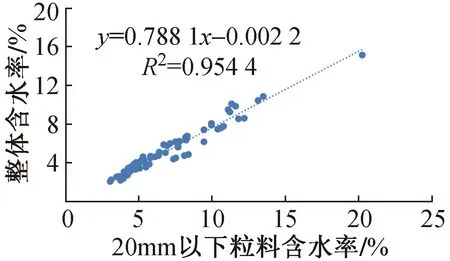
图13 细粒土含水率与整体含水率关系Fig.13 Water content of fine-grained soils in relation to overall water content
3.4 土石混合料压实质量快速检测方法
总结上述分析成果,得到最终的压实质量快速检测方法流程:①第1步 选取试验区同时开展灌水法密度试验、PFWD试验和水分仪测试试验;②第2步 建立PFWD检测过程中位移时程曲线与灌水法结果中湿密度的映射模型;③第3步 根据同测点的水分仪测试含水率、细粒料含水率以及整体含水率数据,建立水分仪测试含水率与整体含水率的计算关系式;④第4步 待验证相关模型计算误差满足工程需求后,后续施工过程中直接进行PFWD和水分仪测试法,并根据检测数据快速计算测点压实质量情况。
虽然在使用该方法前仍需要进行几百组的灌水法、动态变形模量测试试验以建立湿密度与位移时程曲线的映射模型,但相较于动辄上万个测试点位的土石混合料填方工程,这样的测试数据量尚在可接受范围内,整体检测效率相较灌水法得到了极大幅度的提升。且对于变异性较弱的土石混合料其训练神经网络所需要的数据量还可能进一步减少。现场应用过程中,PFWD技术测试数据、水分仪测试数据均可实时上传云端,基于这些数据采用预先训练好的模型实时计算测点湿密度、含水率和压实系数,可在第一时间给出测点压实质量结果,从而进一步提高该方法的可行性。
4 结语
本文通过现场试验和理论分析的方法得到一套完整的土石混合填料压实质量快速检测方法,主要结论如下。
1)动态变形模量难以直接与湿密度、干密度和含水率等压实质量表征参数建立相关关系,二者相关性较低。
2)PFWD检测过程中的位移时程曲线与填料湿密度存在较强的相关性,可以通过BP神经网络建立二者联系,并且基于遗传算法可以进一步提高神经网络映射模型的稳定性,通过预实验阶段训练的神经网络模型,可以在后期施工阶段采用PFWD技术快速得到测点湿密度。
3)通过水分仪测试得到的细粒料含水率与烘干法得到的含水率具备极强线性关系、同时细粒料含水率与填料整体含水率同样具备强线性关系,借助上述关系可以简单建立水分仪测试含水率与测点整体含水率的相关关系,从而实现快速检测含水率的目标。
4)本文总结得到的土石混合填料压实质量快速检测方法基础数据均来源于工程实践,所有分析数据均为现场随机选取,不受限于填料类型、含石量和含水率,具备较高的现场实用价值,可有效解决传统检测方法效率低的问题。

