黏土地层深基坑开挖对邻近建筑物影响研究*

李忠超,贾 琪,冯 恒,唐合棋

(1.武汉市市政建设集团有限公司,湖北 武汉 430023;2.湖南大学土木工程学院,湖南 长沙 410082)

0 引言

近年来,我国城市地下空间得到飞速发展,在大规模开发城市地下空间的同时,不可避免会遇到新建深基坑近接既有建筑物的情况。基坑开挖卸载会引起地层应力释放,从而引起周围土体位移［1-3］和既有建(构)筑物变形［4-6］。许多学者采用了现场实测、数值模拟、模型试验和理论分析等手段研究基坑开挖对邻近既有建筑物的影响。郑刚等［4］通过现场实测和数值模拟,研究了围护墙变形、地表沉降与建筑物变形之间的联系。Son等［5］通过物理模型试验和数值模拟,结合建筑物变形和破坏的实例研究,评估砌体结构变形与破坏之间的关系。Pickhaver等［6］将砌体结构等效为Timoshenko梁并评估地层损失对建筑物的影响。

然而,已有研究大多探究地表沉降和建筑物变形之间的联系,既有建筑物-土体-基坑关联机制方面的研究较少,而围护结构变形的大小和形状将导致不同类型的土体沉降剖面,建筑物沉降又与土体沉降密切相关,因此很有必要分析建筑物-土体-基坑相互作用机理。此外,现有研究通常假设基坑与附近建筑物的相互作用为平面问题,而忽略了其三维空间效应,从而不能准确地揭示基坑开挖引起的邻近建筑物实际响应规律。

本文基于武汉和平大道南延(中山路—张之洞路)工程北侧某深基坑开挖工程案例,通过现场实测和三维数值模拟研究基坑开挖对邻近既有建筑物的影响,获得了基坑开挖作用下既有建筑物沉降、挠曲变形和最大角变量变化规律,揭示了基坑-墙后土体-既有建筑物相互作用机理,分析了坑角效应对建筑物变形的影响,最后根据建筑物破坏准则评估基坑开挖对邻近建筑物的破坏程度。

1 工程概况

1.1 项目概况

基坑平面和剖面分别如图1和图2所示。基坑位于邻近已建建筑物东侧,基坑围护结构由C30地下连续墙结合2道混凝土支撑和1道钢支撑组成,钢支撑预应力约166kN。基坑平面形状近似为梯形,南侧和北侧边长分别约28.5m和21.3m,长为94m。地下连续墙厚1m,深度为27.5m,穿越②6粉质黏土夹粉土,进入③粉砂夹粉土、粉质黏土的深度约1m。基坑开挖深度为16.2m,施工顺序如表1所示。建筑物外形轮廓为长条形,长58.8m,宽33.7m,采用筏板基础,承重体系为框架结构,层数8层,高36.5m,距基坑最小距离16.8m,建筑物立面如图3所示。

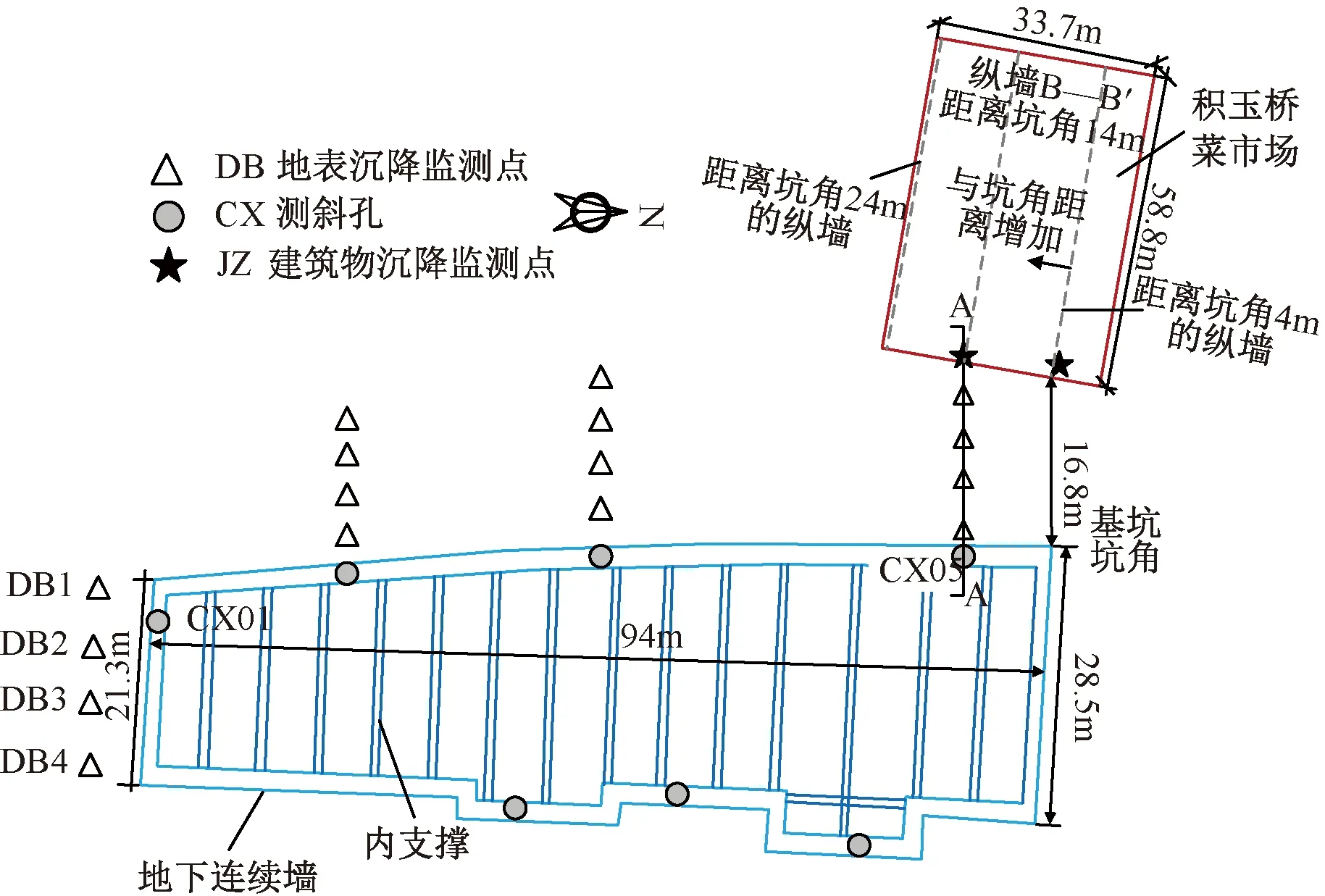
图1 场地平面及监测点布置Fig.1 Plan view of the site and monitoring point layout

1.2 工程地质条件

场地为典型黏土地层,属于长江冲洪积一级阶地,地下水位位于地表下14.8m。通过土体基本物理力学特性室内外试验,包括含水量、常规三轴试验、标准贯入试验、旁压试验和剪切波速测试等,获得了主要土层的物理性质指标,如表2所示。

表2 土体基本物理性质Table 2 Basic soil physical properties

基坑开挖范围内地层包括①3素填土、②1粉质黏土、②2黏土和②3粉质黏土等,基坑底以下一定范围内(-16.800～-26.500m)为②粉质黏土夹粉土。根据水文地质资料,地下水位在-14.800m以下,对基坑施工影响较小。

1.3 现场实测

为研究基坑开挖对邻近建筑物影响,现场布设了地表沉降监测点、建筑物沉降监测点和地下连续墙水平位移监测点。如图1所示,沉降监测点均布置在垂直围护结构的断面上,所有监测点均在基坑开挖前布设完毕。监测点安装方式如下：将钢筋锚入地表以下并用混凝土包裹加固,在建筑物墙面埋入弯成“L”形的φ14圆钢筋并用混凝土浇筑固定,使用水准仪分别监测地表沉降和建筑物沉降;采用测斜仪测量埋设在地下连续墙中的测斜管,监测基坑开挖期间围护墙的水平位移。

2 三维有限元模拟

本文采用PLAXIS 3D进行三维有限元数值模拟,模型参数和计算步骤如下。

2.1 结构参数

为便于建模及计算,地下连续墙、基坑底板、楼板和砌体建筑均采用6节点板单元模拟,混凝土支撑、钢支撑、梁和柱采用3节点梁单元模拟,均假定为各向同性的线弹性材料。在分析中,考虑到施工缺陷等因素,结构单元刚度相对设计值均折减20%［7］。各结构单元计算参数如表3所示。

表3 结构计算参数Table 3 Structural calculation parameters

2.2 土体参数

研究表明,不考虑土体小应变现象会明显高估基坑开挖引起的变形量,该结果将导致针对坑外建筑物的变形研究存在较大的误差。Burland等［8］研究表明小应变水平下土体刚度对基坑开挖引起的隧道变形有显著影响。Brinkgreve等［9］认为,只有考虑土体小应变现象的模型才能合理地预测开挖引起的土体或隧道变形。因此,本文土体采用10节点楔形体单元,其应力-应变关系通过考虑小应变刚度行为的小应变土体硬化模型(HSS模型)模拟。

(1)

式中：e0为土体初始孔隙比。

γ0.7的取值范围较小,Brinkgreve等建议可采用下式计算γ0.7：

(2)

式中：c′和φ′分别为有效黏聚力和有效内摩擦角;σ1′为土体竖向有效应力,计算时可取对应土层中间位置竖向有效应力;K0为静止侧压力系数。

对于影响基坑开挖的主要土层①3素填土、②黏土和③粉砂夹粉土、粉质黏土采用HSS模型,其余强度和刚度较大或位于基底以下较深处的土层(⑩1强风化含粉砂泥岩、⑩2-2中风化含粉砂泥岩和⑩3中微风化含粉砂泥岩)采用莫尔-库仑模型。本基坑开挖时间相对较短,且土体渗透系数相对较低,因此数值计算中土体强度指标采用总应力指标(固结快剪)。各土层计算参数如表4所示。

表4 土层计算参数Table 4 Input soil parameters

为消除模型范围对计算结果的影响,模型侧向边界取4倍基坑最大开挖深度的距离［7］,即225m(长)×198m(宽)×60m(高)。边界条件方面：模型顶面自由,底部边界受水平和垂直位移约束,侧面边界受水平位移约束。计算过程中,不考虑基坑分区开挖和基坑降水,土体位移仅由基坑开挖引起,基坑开挖前位移重置为0。地下水位以下土体在开挖完成后设置水位深度位于开挖面,开挖土体水力条件设置为干,周围地层的水位仍为初始潜水位,基坑周围地层在上述水头差下向坑底发生渗流。有限元模型如图4所示。

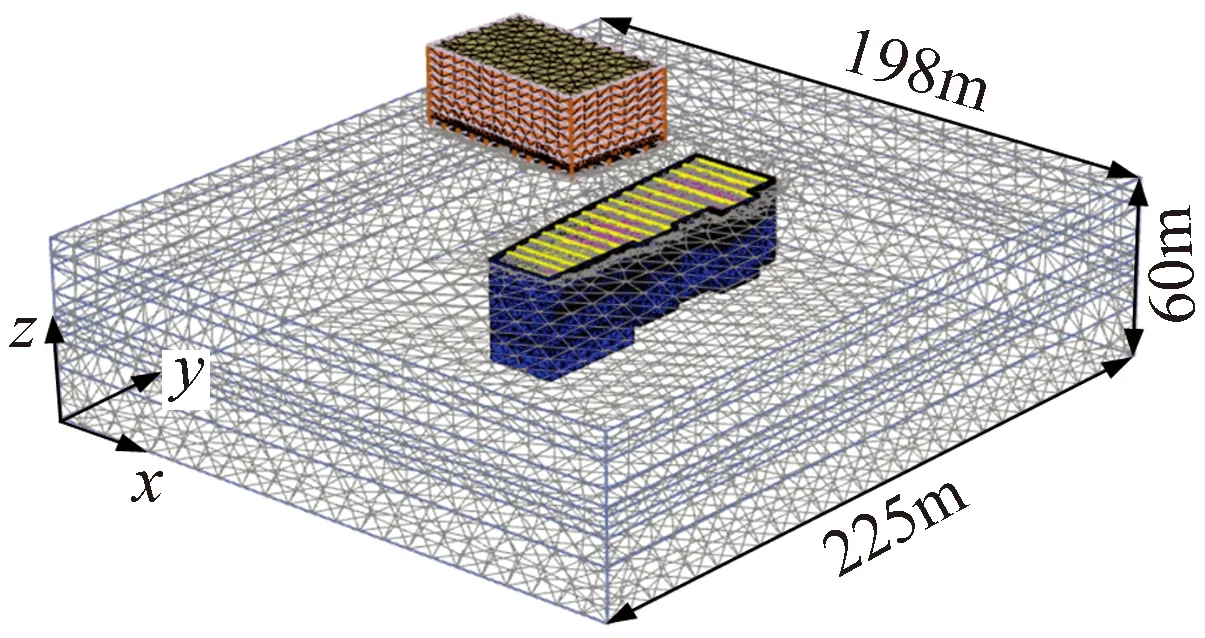
图4 三维有限元模型Fig.4 Three-dimensional FEM model

2.3 模型验证

通过比较各施工阶段DB1～DB4测点地表沉降和CX01,CX05测点围护墙水平位移的实测值与数值模拟计算值来验证上述参数和模型的合理性。如图5所示,地表沉降实测和计算值随着基坑开挖卸载增大而增大,且两者为凹槽形沉降,沉降大小也非常接近(最大实测值为-4.4mm,最大计算值为-4.6mm)。

图5 地表沉降实测值与计算值Fig.5 Measured and calculated ground settlements

如图1所示,CX01测点位于基坑南边侧墙,缺乏第1道支撑的约束作用,因此变形呈现悬臂形。相比而言,CX05测点位于基坑西边侧墙,由于存在第1道支撑约束,其变形呈现纺锤形。围护墙最大实测位移为6.4mm,最大计算值为7.1mm,两者较为吻合。

本基坑土方开挖分为3层,采用分块分区开挖。由于围护墙变形较小,为了抢工期,实际施工将第3层土方开挖到一定程度再施工第3道钢支撑,所以主要变形发生在第2层土方开挖期间,后续的第3层土方开挖引起的变形增量很小。

从图5和图6可以发现实测结果与模型计算结果吻合较好,这说明本文所取的结构参数、土体参数和计算模型是合理的。

图6 CX01测点围护墙水平位移实测值与计算值Fig.6 Measured and calculated wall deflections on CX01

3 建筑物对邻近基坑开挖的响应

3.1 建筑物变形特点

Ou等［12］认为基坑开挖引起的地表沉降剖面主要有两种类型,即凹槽形和三角形,而基坑开挖卸载作用下引起的围护结构变形是导致地表沉降的主要原因［13］,围护结构变形的大小和形状将导致不同类型的地表沉降和土层沉降剖面,而建筑物沉降与土体沉降密切相关,因此很有必要分析建筑物-土体-基坑关联机制。

通过比较基坑开挖期间地表沉降、围护墙变形和建筑物沉降实测值与计算值可以发现：A—A断面地表沉降实测值、计算值与Ou等［12］经验曲线非常接近;主次沉降区的分布也与其基本吻合;围护墙变形和建筑物沉降实测值与计算值大小和趋势较为一致(见图7～9),这从另一方面证明了模型与计算的准确性。

图7 A—A断面围护墙水平位移(CX05测点)Fig.7 Diaphragm wall displacement of section A—A (CX05)

地下连续墙在开挖的初始阶段出现较小的墙体侧移,当开挖进行到较深处时,墙体上部的侧移受到内支撑的约束作用,墙体侧移将转移到更深处,出现了内凸形变形模式,实测最大水平位移为12.4mm,计算最大水平位移为12.0mm(见图7)。

由于墙顶受第1道混凝土支撑约束作用几乎不产生侧移,只在第3道钢支撑和基底之间有最大侧移,使得紧邻围护墙的土体沉降很小,而墙后出现了明显的沉降槽(凹槽形),即转化为与围护墙内凸型变形模式一致的地表沉降剖面(见图8)。最大沉降发生在距墙体0.5倍基坑开挖深度处,为-2.9mm;超过主要影响区［12］后,沉降曲线迅速减小;约2.3倍开挖深度处,沉降曲线的上凸挠曲最为显著;4倍开挖深度后土体几乎不受基坑开挖影响,这与Lim等［7］研究结果一致,即基坑开挖的影响范围大致为4倍基坑开挖深度。

图8 A—A断面归一化沉降曲线Fig.8 Normalized settlement curves of section A—A

建筑物仅跨越墙后地表沉降槽的上凸区域,并未同时跨越沉降槽最低点及上凸曲率最大点［4］,其沉降曲线和地表沉降曲线在大小和趋势上基本一致(见图9)。但由于建筑物自身约束作用,使得地表沉降曲线的上凸区域沉降程度略微降低,沉降曲线的变化更为平缓,说明建筑物对土体约束作用较小,并和土体协调变形。而建筑物沉降受基坑开挖影响较大,随开挖卸载量增大而增加,施加内支撑能很好控制建筑物沉降,底板浇筑完成后建筑物基本保持稳定不再发生沉降。

图9 JZ01监测点建筑物沉降-时间曲线Fig.9 Building settlement-time curve of point JZ01

建筑上沿建筑物长轴方向布置的墙称为纵墙,如图1中虚线所示,其挠曲变形分为3种：下凹挠曲变形、上凸挠曲变形和S形挠曲变形。本文中建筑物跨越墙后沉降槽的上凸区域,其挠曲变形呈现上凸挠曲变形(见图10),且建筑物在沉降槽上凸曲率最大点时有最大上凸挠曲变形(0.9mm),即建筑物距离围护墙38.5m时,建筑物的上凸挠曲变形最为显著。一般来说,上凸挠曲变形造成的建筑物损坏比下凹挠曲变形更严重［4］,因为前者的建筑物拉伸裂缝发展得更早、更快。而建筑物挠曲变形趋势及挠曲程度取决于建筑物所跨区间内土体沉降曲线的挠曲变形特征,土体沉降曲线又取决于围护墙变形模式,因此在基坑开挖期间要控制好围护墙变形,避免引起过大侧移而导致坑外土体和建筑物出现过大或不均匀沉降。

图10 建筑物纵墙墙体B-B’挠曲变形曲线Fig.10 Flexure wall (B-B’) deformation curve in longitudinal direction

3.2 坑角效应

基坑长宽比约为0.94,开挖深度为16.2m,长、宽尺寸较小,而深度较大,三维空间效应显著。基坑开挖的空间效应主要体现在坑角效应上,而建筑物恰好位于坑角处,坑外土体的不均匀沉降将导致建筑物发生不均匀沉降和挠曲变形,因此有必要分析坑角效应对建筑物变形的影响。建筑物沉降云图如图11所示。

图11 建筑物沉降云图Fig.11 Contours of building settlement

如图12所示,坑外地表沉降最大值在距基坑边(0.5～0.8)倍开挖深度处,这与Ou等［14］在某深基坑工程中得出的结论相近。由于坑角效应的影响,墙后地表沉降在沿基坑边长方向上出现明显的差异。d为地表沉降曲线与左上角坑角的距离,当d=90m,位于右上角坑角处时,坑角的约束作用最强,此时有最小地表沉降-0.9mm;而当d=0m,即位于左上角坑角处时,地表沉降相比要大些,为-2.3mm,原因是右上角坑角相比更为尖锐,坑角效应更强,对地表沉降的约束作用更大。而在基坑长边中部地表沉降明显大于坑角区域的地表沉降,且距离坑角越远,地表沉降越大,最大地表沉降可达-5.3mm,约为坑角处最小地表沉降的5.9倍。根据Finno等［15］的研究,坑角效应的影响区域约为3倍开挖深度,即本文基坑长边中部基本可忽略坑角效应的影响,此时围护结构及土体的受力与变形可近似视为平面应力-应变状态,且土体变形达到最大。

图12 基坑距坑角不同距离处地表沉降曲线Fig.12 Surface settlement curve at different distance from excavation corner

图11给出了底板施工完成后基坑坑角处建筑物的整体沉降,右侧数字代表建筑物的沉降,它显示了建筑物的整体沉降和倾斜情况［16］。由于坑角效应影响,建筑物沉降并有向基坑方向倾斜的趋势,裂缝一般仅发生在垂直于基坑边线的墙体上,这与丁勇春等［17］的研究是一致的。

从墙沉降与挠曲变形如图13,14所示。图13所指的纵墙是指与纵墙B-B’平行,且距基坑坑角不同距离(0.5,4,9,14,19,24m)的纵墙,其中纵墙B-B’距离坑角14m。从图13和图14可以发现,由于坑角效应的存在,建筑物沉降在沿基坑长边方向上将呈现明显的差异,其中,在紧邻坑角的区域受坑角效应影响较大使得建筑物沉降最小(-0.51mm),而在距坑角较远处沉降为-2.34mm,约为坑角处沉降的4.6倍。距坑角不同距离处的纵墙仍在地表沉降槽上凸曲率最大点时有最大上凸挠曲变形,其中坑角处挠曲变形为0.14mm,距坑角较远处挠曲变形为1.0mm,约为坑角处的7.1倍。这说明坑角效应约束了建筑物的沉降和挠曲,即当建筑物纵墙垂直于基坑边,且距坑角距离小于1.2倍开挖深度时,坑角效应对建筑物变形起有利作用。

图13 距坑角不同距离处纵墙沉降曲线Fig.13 Settlement curve of longitudinal wall at different distance from excavation corner

图14 距坑角不同距离处纵墙墙体挠曲变形曲线Fig.14 Flexure deformation curves of longitudinal wall at different distance from excavation corner

3.3 建筑物损坏程度评估

王卫东等［18］认为角变量β与建筑物内部结构扭曲或开裂直接相关,评估建筑物的附加变形主要是确定角变量β,所以将β作为评估基坑开挖对建筑物损坏程度的标准,其计算公式如下：

βij=θij-ω=δij/Lij-ω=(δi-δj)/Lij-ω

(3)

式中：θij为两点间差异沉降与两点间水平距离比值;ω为刚体转动量;δij为任意两点i,j之间的沉降之差;Lij为i,j两点的水平距离。

本文中ω较小,可取其值为0,这能得到比较保守的结果。同一断面不同两点之角变量并不相同,但我们关注的是最大角变量,即最大角变量在容许范围内,那么其余角变量也必然在范围内。所以很有必要分析不同断面和同一断面不同两点之间的最大角变量,如图15所示。

图15 距坑角不同距离处最大角变量-两点之间距离关系曲线Fig.15 Curves of maximum angular distortion-distances of any two points at different distance from excavation corner

由图15可知,由于坑角效应的影响,近坑角处的建筑物沉降相比远坑角处要小,使得近坑角处的最大角变量小于远坑角处的最大角变量。当任意两点间隔1m时,有最大角变量,即角变量最大值近似等于建筑物沉降曲线切线斜率的夹角,最大角变量值为1.26×10-4。Bjerrum［19］总结了建筑物损坏程度与角变量之间的关系,如表5所示。

表5 角变量与建筑损伤程度的关系Table 5 Relationship between angular distortion and damage degree of building

可以发现最大角变量小于建筑物容许的角变量(1.26×10-4<1/750)。在基坑开挖时现场人员也未发现建筑物产生任何裂缝或其他破坏,即基坑施工并未对建筑物产生损坏,说明本文分析和现场实测结果基本吻合。

4 结语

本文基于武汉和平大道南延(中山路—张之洞路)工程北侧深基坑开挖工程,研究了基坑开挖对邻近既有建筑物的影响规律,通过现场实测和三维数值模拟,得到以下结论。

1)建筑物挠曲变形趋势及挠曲程度取决于建筑物所跨区间内土体沉降曲线的挠曲变形特征,土体沉降曲线又取决于围护墙变形模式,因此在开挖期间要控制围护墙变形,避免墙体过大侧移而导致坑外土体和建筑物出现过大沉降或不均匀沉降。

2)建筑物自身约束作用,使得地表沉降曲线的上凸区域沉降程度略微降低,沉降曲线的变化更为平缓,说明建筑物对土体约束作用较小。建筑物沉降受基坑开挖影响较大,随开挖卸载量增大而增加,施加内支撑和底板能很好控制建筑物沉降。

3)坑角效应会明显改变土体位移场从而导致建筑物在空间上发生不均匀沉降和挠曲变形。坑角角度越尖锐,坑角效应对坑外土体的约束作用越强,建筑物沉降和挠曲变形更小。

4)坑角效应约束了建筑物的沉降和挠曲,即当建筑物纵墙垂直于基坑边,且距坑角距离小于1.2倍基坑开挖深度时,坑角效应对建筑物变形起有利作用。

5)近坑角处的最大角变量小于远坑角处的最大角变量,角变量最大值近似等于建筑物沉降曲线切线斜率的夹角。