风嘴外形对钝体钢箱梁铁路斜拉桥涡振性能的影响

黄 林，董佳慧，王 骑，廖海黎

(1.西南交通大学 土木工程学院，四川 成都 610031；2.风工程四川省重点实验室，四川 成都 610031)

随着我国铁路桥设计和建设技术的进步,钢箱梁由于其刚度大、维护便利及便于施工安装等特点,被逐渐应用到了大跨度铁路桥中。传统的扁平钢箱梁具有自重轻、横向整体受力性能好以及后期养护方便的优点[1],但同时也存在竖向及扭转刚度较小,无法满足大跨度铁路桥设计要求的缺点。从结构设计方面考虑,现通常通过增大梁高以提高梁体的竖向刚度,从而满足铁路桥行车的设计需求,这也使得最终的箱梁断面呈现出明显的钝体特征。

桥梁涡激振动是一种具有限幅特性的的风致振动,通常发生在低风速下的大跨度桥梁中。2020年,我国已建成的广东虎门大桥与武汉鹦鹉洲长江大桥均发生了明显的涡激振动现象,涡振的发生使得桥梁的正常运营受到严重影响,而相比公路桥梁,铁路桥梁的涡激振动会严重影响铁路桥上列车的正常行驶,导致更为严重的安全问题,因此在设计中应做到坚决避免。

大量研究表明,气流流经外形具有典型钝体特征的桥梁断面时,会发生明显的漩涡生成、合并与脱落现象,从而产生周期性的气动力[2-5]。因此较一般公路桥,气动外形呈现更为明显钝体特征的铁路桥箱梁断面存在涡激振动的隐患更大[6]。同时,相比简单的几何钝体断面,在铁路桥桥面设置的一系列附属构件(如轨道板、轨道以及中央防抛网)也会在一定程度上降低主梁的涡振性能[7]。

针对桥梁断面的涡振特性与气动措施研究,Nagao等[8]总结了桥面栏杆位置与尺寸对扁平箱梁涡振响应的影响规律。Larsen等[9-10]的研究也表明栏杆对于箱梁表面的气流分离及漩涡脱落形态影响显著,较施工态断面,设置栏杆后的成桥断面涡振性能显著降低,而通过在栏杆处设置导流板可以有效减弱栏杆对来流的影响。李浩弘等[11]采用CFD数值计算与风洞试验对某宽体扁平箱梁的涡振特性研究发现,增大栏杆透风率也能显著减弱栏杆对来流的影响,但该方法受到栏杆设计规范的限制,在实际应用中无法真正做到大幅度提高栏杆透风率,而研究还发现内移检修车轨道可以用于改变箱梁下部的流场,从而达到优化梁体涡振性能的作用。孟晓亮等[12]针对某公路桥钢箱主梁的研究发现,减小风嘴角度可以有效改善其梁体的涡振性能。李浩[13]通过对某钢箱梁主梁宽高比为3.8的铁路斜拉桥进行风洞试验,发现针对铁路桥箱梁断面,减小风嘴角度同样可以起到改善涡振性能的作用。

目前,大部分针对钢箱梁涡振性能及优化措施的研究都以扁平箱梁或带挑臂的梯形箱梁为出发点进行,关于钝体钢箱梁铁路桥涡振制振方面的研究较少,但综合以上研究可以发现[12-14],对于封闭式箱梁断面,减小风嘴角度均能改善梁体的涡振性能。

本文以某主跨为672 m的钝体钢箱梁铁路斜拉桥为工程背景,通过一系列1∶50节段模型风洞试验对比不同形状风嘴的制振效果,研究风嘴外形对钝体钢箱梁铁路斜拉桥涡振性能的影响,同时利用CFD研究不同外形风嘴对于主梁涡振性能的影响机理,进而提出一种带平台的三角形下行风嘴制振措施,并采用1∶25大比例尺试验验证该风嘴的有效性。

1 主梁涡振性能

1.1 工程背景

本文以一座(2×50+224+672+174+3×50) m=1 320 m跨径布置的铁路斜拉桥为背景,该桥采用钢箱主梁,梁高为4.8 m,全宽为36.7 m,宽高比为7.65,桥面上布置有检修道、轨道板、管线槽与中央防抛网(高度为3 m,透风率为65%)等附属设施,具体见图1。

1.2 试验及涡振限值设置

目前国内外还没有针对铁路桥梁涡振振幅限值取值的相关规范条文,TB 10621—2014《高速铁路设计规范》[15]也无关于大跨度高速铁路斜拉桥的振动幅值允许值规定,因此本文对涡振振幅的评判参考如表1所示的4种规范。但考虑铁路桥梁发生涡振时,振幅对铁路行车影响是动态的,且现今我国列车的运营速度也明显高于汽车行驶速度,因此出于安全系数考虑,取表1所列限值中的最小值为最终涡振振幅允许值,选取日本指南[16]中的142 mm竖向振幅限值与英规[17]中的0.179°扭转振幅限值。

表1 各国规范涡振振幅限值

1∶50节段模型试验在西南交通大学XNJD-1风洞大气边界层风洞中进行,试验段截面尺寸为2.4 m×2.0 m。节段模型长度采用2.095 m,试验中各工况阻塞度均小于5%,满足规范要求[18]。模型表面采用蒙皮工艺,其余附属构件均采用ABS塑料板制作。

大量研究表明,桥梁的涡振响应与其阻尼比大小呈明显的负相关关系[19-20]。然而目前还没有一种被广泛接受的准确评价桥梁结构阻尼的方法,也没有针对大跨度钢箱梁铁路桥风洞试验阻尼比取值的相关规定,故试验阻尼比参考以往铁路桥风洞试验研究取值(0.5%)[21],试验具体参数见表2。表2中,m为系统的质量;Im为系统的质量惯性矩;fh与ft分别为系统的竖向和扭转振动频率。

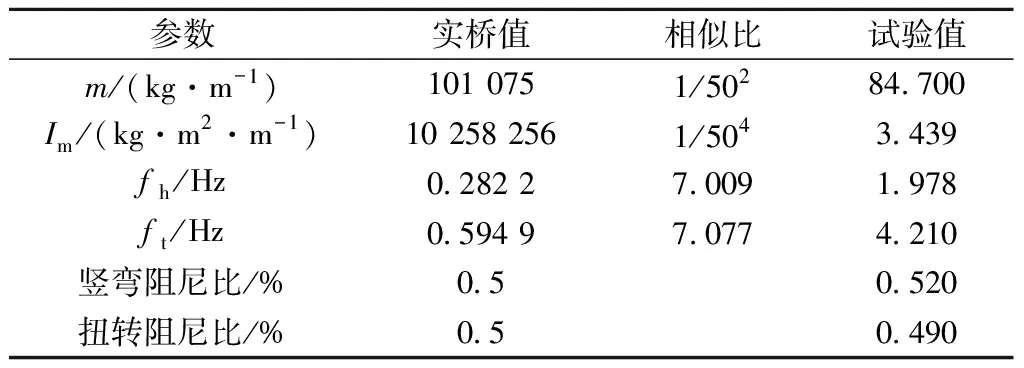
表2 1∶50节段模型试验参数

1.3 原设计钢箱梁断面涡振性能

风洞试验均在均匀流中进行,试验风速范围为0.5～6 m/s,对应实桥风速范围为3.5～42 m/s,风速间隔为0.15 m/s,对应实桥风速间隔约为1 m/s。试验结果见图2,图2中风速和振幅数据均已换算至实桥,下文同理。

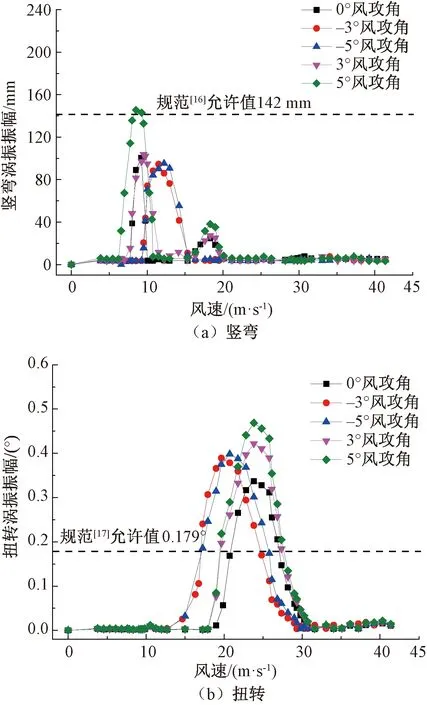
图2 原设计断面主梁涡振响应

由图2可见:

(1)断面在0°、3°与5°攻角下均存在两个竖弯涡振区间,分别为6～12 m/s的低风速区间与16～20 m/s的高风速区间,其中低风速涡振区间内的响应较大,最大振幅均超过100 mm,且在5°风攻角下振幅超过规范允许值。高风速涡振区间内梁体涡振振幅较小,最大振幅均小于40 mm。在-3°、-5°风攻角下,原设计断面仅存在一个竖弯涡振区间(9～16 m/s),最大振幅均超过90 mm。

(2)在各测试风攻角下,原设计断面均存在一个扭转涡振区间,且该区间所处风速较高,在16～30 m/s范围内,最大振幅也均超过规范允许值,较竖向涡振响应,该断面的扭转涡振响应更为显著。

2 风嘴上行、下行及对称外形对钝体钢箱梁涡振性能影响

梁体的涡振性能对其气动外形的变化十分敏感,气动措施是提高断面涡振性能的常用方法,大量研究成果[13,22]表明,风嘴处的外形变化影响作用尤为明显。因此本文设计了具有不同气动外形的风嘴,通过风洞试验测试安装了不同风嘴的主梁断面涡振响应,并通过计算流体动力学(CFD)数值模拟得到主梁周围的流场结构,从而研究风嘴外形变化对断面涡振性能的影响机理。

2.1 节段模型涡振试验

本次试验重点考察风嘴长度相同的情况下(实际长度均为4 m),风嘴尖角朝向变化对风嘴制振性能的影响,故本文将风嘴尖角位于对称线上方、下方和对称线处的风嘴分别命名为上行风嘴、下行风嘴与对称风嘴,具体分类见图3。试验所选取的1#风嘴(上行风嘴),2#风嘴(对称风嘴)与3#风嘴(下行风嘴)具体见图4。

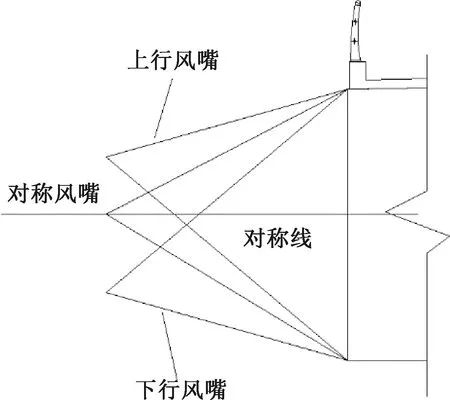
图3 风嘴分类示意

图4 1#～3#风嘴示意(单位:cm)

前文研究表明,该钝体箱梁在5°风攻角下的涡振响应最为显著。考虑代表性和特殊性,选择在0°与5°攻角下进行后续断面涡振响应试验,为使试验现象明显,试验中均采用低阻尼比,竖弯与扭转阻尼比取值均为0.16%。安装不同风嘴后主梁最大涡振振幅见表3,表中振幅数据均已换算至实桥,下文同理。

表3 1#～3#风嘴工况最大涡振幅值

由表3可知,在0°风攻角下,三种风嘴均能显著抑制主梁的竖弯涡激振动且制振能力几乎相同,但对于主梁扭转涡激振动,分别加装1#、2#与3#风嘴断面的最大涡振振幅依次从大到小排列,且后者最大振幅均较前者降低10%以上。在5°风攻角下,1#、2#与3#风嘴三种风嘴对主梁竖弯与扭转涡振振幅降低作用均依此提升,且后者最大振幅较前者均降低8%以上。可以发现,对该钝体箱梁断面,在风嘴长度相同的情况下,三种风嘴对主梁竖弯与扭转涡振制振能力排序均为3#>2#>1#风嘴,即下行风嘴效果最佳。

2.2 断面绕流数值模拟

为了研究不同外形风嘴对于钝体钢箱梁涡振性能的影响机理,借助计算流体动力学(CFD)数值模拟技术[23],通过Fluent软件分别对加装了1#风嘴(上行风嘴)与3#风嘴(下行风嘴)断面在静止状态下的非定常绕流进行2D瞬态仿真模拟,计算断面见图5。

图5 计算断面简图

本次数值模拟计算采用SSTk-ω湍流模型[24],该模型是一种将k-ω模型和k-ε模型相结合所形成的一种改进型湍流模型,模型既充分模拟在远离壁面区域处的湍流流动,又考虑了湍流剪应力的传播,且合并处理来源于ω方程的交叉扩散,使得该模型的计算结果具有较高的可靠度和精确度。

本文采用FLUENT18.2软件进行桥梁断面周围流场的数值模拟,计算模型缩尺比选为1∶50,计算风速为3 m/s。计算域设置见图6,计算域总尺寸为15B×28B(B为加装1#风嘴断面宽度),根据以上参数设置,计算模型沿顺风向的阻塞率不大于5%,流域上下对称边界对计算断面周围的流动干扰可以忽略[25]。计算域的左边界设置为速度入口,即Velocity-inlet,入口速度设置为3 m/s,压力采用默认设置,湍流强度设置为0.5%,湍流长度尺度设置为0.073 m,流体从此入口流入;计算域的右边界设置为压力出口,即Pressure-outlet,湍流强度、湍流长度尺度和压力设置同左边界,流体从此出口流出;桥梁断面设置为无滑移壁面,即No-slip wall;四种边界条件的其他设置采用Fluent中的默认值。其中内层底层网格厚度设为7.6×10-5m,数值计算中各断面的y+值均小于7(y+为近壁面流体流动无量纲距离)。

图6 计算域与网格划分

采用基于压力的求解器进行瞬态模拟,压力-速度耦合算法采用SIMPLE,梯度项离散算法选用Least Squares Cell Based Method,压力项、动量方程、湍动能k和湍流耗散率ω选用二阶迎风格式进行离散,选用二阶隐式方法求解瞬态项,时间步长设置为0.000 025 s,每个时间步内的收敛残差控制在10×10-5以内,初始化方法采用混合初始化方法。

为确保数值模拟结果的可靠性,对迭代计算过程中流域入口处的风速、静压、总压、k和ω的值进行监控,结果见图7。由图7可知,速度、k和ω不随时间发生改变,入口处静压和总压在计算稳定后趋于平稳。同时为了确保数值模拟在低残差(10×10-5)下的收敛性,计算过程中监测了桥梁断面的静力三分力系数,加装1#风嘴断面的升力系数时程见图8。待三分力系数计算稳定一段时间后,如图8中红色方框内所示,升力系数以相同的振幅和频率进行波动,其振幅和频率不会随着迭代而改变,此时认为计算可以达到收敛。

图7 流域入口检测

图8 加装1#风嘴断面升力系数随迭代变化时程

加装1#风嘴断面在3 m/s计算风速下静态绕流的气动升力CL(t)的频谱图见图9。由图9可知,在40 Hz 频率以内仅存在1个卓越频率fsimulation=4.603 3 Hz,通过计算得到对应斯托洛哈数St(simulation)=0.147 3。代入加装1#风嘴断面主梁在风洞试验中的扭转涡振起振风速20.3 m/s,计算得到对应的St(test)=0.140 7。将St(simulation)与St(test)相比,误差仅为4.7%,计算结果与试验值吻合较好,表明本文所采用的CFD数值计算方法可以较好地模拟计算断面表面的绕流情况。

图9 加装1#风嘴断面CL(t)频谱

为确定较优的计算网格数量,在已经确定尺寸范围的计算域基础上,对加装1#风嘴断面设置三种数量的网格进行计算,通过将计算断面升力系数时程的St与试验结果对比,用以确定数值模拟的准确性。网格数量及计算结果见表4,可以发现在65万网格数内,随着网格的加密,计算误差呈递减趋势,网格越密,计算得到的St越接近试验结果。其中粗糙网格数量与中等网格数量相差22 万,两者计算误差相差3.4%,中等网格与精细网格的数量相差为24万,两者计算误差仅相差0.5%,可以发现当网格数量较低时,加密网格对St的改善程度较为明显,但超过41万网格数量后,加密网格对St的改善程度十分有限,而使用精细网格将成倍的增加计算资源消耗,因此,本文采用中等网格数量进行后续计算。

表4 不同网格数量计算结果

为了能够完整观察到断面周围各个位置处旋涡的演化情况,选择St(simulation)=0.147 3对应的脱落周期作为观察周期,一个完整周期T内加装1#风嘴断面表明的旋涡演化过程见图10。

图10 加装1#风嘴断面非定常绕流瞬时涡量演化

来流在上游梁端部发生流动分离后,下侧气流在断面斜腹板转角处形成大型旋涡B1,但旋涡B1并没有向下游移动,而是出现了再附现象。上侧气流在外侧栏杆与轨道板之间形成漩涡A1,之后演化为一系列小型漩涡向下游移动,并最终在断面上表面后缘处发展成为漩涡A2,与梁体下方的旋涡B2一起在尾流区发生交替脱落。

加装3#风嘴断面非定常绕流瞬时涡量演化见图11,由图11可知,加装3#风嘴断面的绕流特性与1#风嘴断面主要存在两点差异:

(1)由于下行风嘴上表面处斜率大于上行风嘴,导致与加装1#风嘴断面相比,加装3#风嘴断面上表面迎风侧处形成的漩涡A1远离断面表面,进而使得上表面尾流区漩涡A2的能量显著降低。

(2)由于下行风嘴下表面处斜率小于上行风嘴,导致与加装1#风嘴断面相比,迎风侧风嘴下表面处来流受压缩程度降低,使得加装3#风嘴断面下表面迎风侧处形成的漩涡B1尺寸显著降低。同样,由于背风侧风嘴下表面处气体流动面变宽速率降低,导致下表面尾流区漩涡B2的能量显著降低。

以上两点变化均会导致在尾流区所形成的卡门涡街能量降低,从而降低尾流脱落对梁体产生的周期性压力差。三分力系数时程图见图12,由图12可知,两种断面的三分力系数中对涡振有较大影响的升力系数与力矩系数随时间的变化均是呈正弦曲线。说明梁体受到的卓越周期性涡激力只有一个,其中加装1#风嘴断面的升力系数在-0.003 74～0.036 75之间变化,幅值为0.020 25,力矩系数在0.004 45～0.012 15之间变化,幅值为0.003 85。对比加装1#风嘴断面,加装3#风嘴断面的升力系数变化幅值降至0.006 38,降幅68.5%,力矩系数幅值降至0.001 29,降幅66.5%,两者的降幅均达到65%以上。这也印证了下行风嘴制振效果优于上行风嘴的风洞试验结果。结合涡量演化图的分析可以发现,漩涡尺寸与能量较大且大幅降低的主要是尾流处的卡门涡脱,因此尾流处的卡门涡脱是引起该钝体断面涡激振动的主要原因,下行风嘴能够显著降低尾流涡脱的能量是其能够抑制梁体的涡激振动且制振效果优于上行风嘴的主要原因。

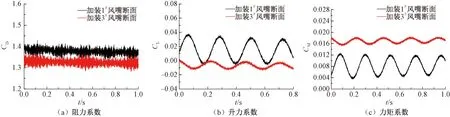
图12 三分力系数时程

3 风嘴细部尺寸对矩形钢箱梁涡振性能影响

通过前文研究可知,风嘴的气动外形会显著影响该钝体箱梁的涡振特性。设置不同角度与不同平台长度的风嘴,采用1∶50节段模型风洞试验在0.16%阻尼比下测试不同工况下主梁涡振的振幅,并结合数值模拟研究风嘴细部尺寸变化对主梁涡振性能的影响机理。

3.1 风嘴角度的影响

以原设计风嘴(5#风嘴)为基础,在仅改变风嘴角度的情况下(具体风嘴详情见图13),研究风嘴角度变化对制振效果的影响,加装不同角度风嘴断面所对应的涡振振幅见表5。

图13 2#、4#、5#风嘴示意(单位:cm)

由表5可知,在0°风攻角下,分别加装2#、4#与5#风嘴断面的竖弯与扭转最大涡振振幅均依次从小到大排列,且前者竖弯最大振幅较后者降低35%以上,扭转最大振幅降低13%以上,在5°风攻角下,分别加装3种风嘴断面的最大涡振振幅排列规律与0°风攻角下规律相同。可以发现,对于该钝体箱梁断面,三种风嘴对主梁涡振制振能力排序由大到小均为2#、4#、5#风嘴,即随着风嘴角度的减小,风嘴的制振能力提高。

采用与第2.2节同样的数值分析方法,分别对加装2#风嘴与5#风嘴断面(计算断面见图14)的非定常绕流进行仿真模拟并研究风嘴角度变化对制振效果的影响机理。

图14 计算断面简图

将断面上表面尾部的旋涡脱落周期作为一个观察分析周期,计算风速下加装5#风嘴(原设计风嘴)断面的某个完整周期内断面的气体绕流及旋涡演化过程见图15。由图15可知,在来流作用下,断面表面主要生成了3处大尺寸漩涡,分别是断面迎风侧下侧转角附近生成的漩涡B1(高度为0.77倍梁高,宽度为0.48倍梁宽)、断面下表面后缘处发生漩涡脱落的漩涡B2(高度0.90倍梁高,宽度为0.31倍梁宽)及断面上表面后缘处发生漩涡脱落的漩涡A1(高度为0.84倍梁高,宽度为0.26倍梁宽)。

图15 加装5#风嘴断面非定常绕流瞬时涡量演化

加装2#风嘴断面的瞬时涡量演化见图16,减小风嘴角度后,断面表面处的漩涡尺寸与能量显著降低,原断面迎风侧下侧转角处的大尺寸漩涡B1变为一系列小尺寸漩涡,原断面尾流处交替脱落的漩涡A1与B1能量均显著降低60%以上,从而显著降低尾流涡脱对梁体产生的周期性压力差,以上变化均会导致断面的涡振性能提升,这也印证了风洞试验结果。能够显著改变迎风侧下表面以及尾流处漩涡的尺寸与能量是风嘴角度变化能影响断面涡振性能的主要原因之一。

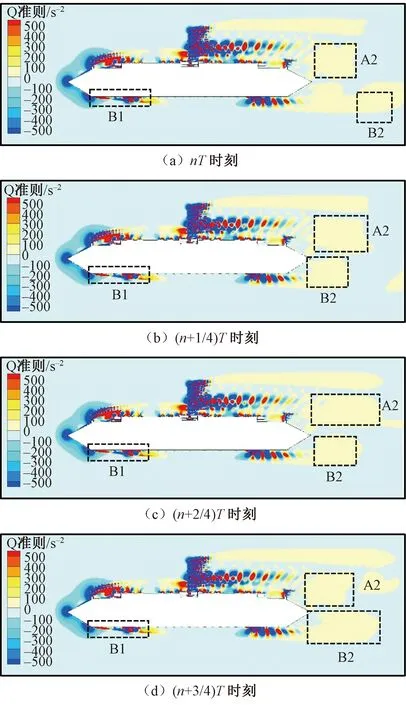
图16 加装2#风嘴断面非定常绕流瞬时涡量演化

3.2 风嘴平台长度的影响

由于下行风嘴制振效果较好,在传统三角形下行风嘴上部设置平台(改变气流在梁体上部的分离点),提出一种带平台的三角形下行风嘴。重点考察风嘴长度相同的情况下(实际长度均为4 m)平台长度对该类型风嘴制振性能的影响(具体风嘴详情见图17),各工况对应的涡振振幅见表6。

表6 6#～8#风嘴工况最大涡振幅值

由表6可知,在0°风攻角下,平台长度较长的7#、8#风嘴均能显著抑制主梁的扭转涡激振动至0.06°以下,6#风嘴的扭转制振效果相对较差,分别加装6#、7#与8#风嘴断面的竖弯最大涡振振幅依次从大到小排列,且后者最大振幅均较前者降低60%以上。在5°风攻角下,分别加装6#、7#与8#风嘴断面的最大涡振振幅依次从大到小排列,且后者最大振幅较前者均降低25%以上。可以发现,平台长度的变化对于风嘴制振性能影响显著,三种风嘴对梁体涡振制振能力由高到低排序为8#、7#、6#风嘴。当风嘴总长度相同时,随着风嘴平台长度的增加,风嘴的制振能力显著提高。

分别对加装6#风嘴与8#风嘴断面(计算断面见图18)的非定常绕流进行仿真模拟并研究风嘴平台长度变化对制振效果的影响机理。

图18 计算断面简图

加装6#与8#风嘴断面的瞬时涡量演化分别见图19与图20,可以发现加装8#风嘴断面气体绕流特性与加装6#风嘴断面的区别主要在于,8#风嘴较长的平台导致来流在迎风侧风嘴上表面的分离点远离主梁外侧防撞栏杆,另一方面8#风嘴上表面处斜率大于6#风嘴,导致风嘴断面上表面迎风侧处形成的漩涡A1远离断面表面以及外侧防撞栏杆,以上两点区别均会导致加装8#风嘴断面在A1处产生的漩涡能量降低且远离断面表面,从而降低该处漩涡对梁体产生的周期性涡激力,提高梁体的涡振性能。

同时可以发现,本文将1#与3#风嘴、2#与5#风嘴、6#与8#风嘴之间的制振效果通过风洞试验与CFD数值模拟进行比对研究,两者所呈现出的规律性均相互匹配,故本次数值模拟的参数设置可为后续的CFD计算提供参考。

3.3 风嘴角度与平台长度的组合影响

通过第3.1节与3.2节的研究发现,对于三角形风嘴,随着风嘴角度的减小,风嘴制振能力提高,对于带平台的三角形风嘴,随着平台长度的增加,风嘴制振能力提高。本节主要研究风嘴平台长度与风嘴角度对风嘴制振性能的组合影响。

在原制振效果显著的8#风嘴基础上,通过增大风嘴角度并减小平台长度形成9#风嘴,见图21。分别加装两种风嘴后主梁的最大涡振振幅见表7,在0°风攻角下,加装8#风嘴断面的竖弯与扭转最大涡振振幅均小于加装9#风嘴断面最大振幅的85%以上,在5°风攻角下,加装8#风嘴断面的竖弯与扭转最大涡振振幅也均小于加装9#风嘴断面最大振幅的50%以上。可以发现,对于该钝体箱梁断面,8#风嘴的涡振制振能力显著优于9#风嘴,即风嘴平台长度与风嘴角度对于风嘴制振能力的影响可以正相加,随着风嘴平台长度的增加与风嘴角度的减小,风嘴的制振能力显著提高。

表7 8#、9#风嘴工况最大涡振幅值

图21 8#、9#风嘴示意(单位:cm)

通过分别测试加装6#、10#与11#风嘴断面(图22)的涡激振动,研究平台长度与风嘴角度这两种影响因素中,哪一种是影响风嘴制振性能的主导因素。其中平台长度的由大到小排序为11#、10#、6#风嘴,风嘴角度的由大到小排序为11#、10#、6#风嘴,即具有较长平台的风嘴,其风嘴角度也较大,而具有较短平台的风嘴,其风嘴角度较小。

图22 6#、10#、11#风嘴示意(单位:cm)

各工况对应的涡振振幅见表8,在0°风攻角下,分别加装6#、10#与11#风嘴断面的竖弯与扭转最大涡振振幅均依次从大到小排列,在5°风攻角下,分别加装3种风嘴断面的最大涡振振幅排列规律与0°风攻角下规律相同。可以发现,对于该钝体箱梁断面,三种风嘴对主梁涡振制振能力由高到低排序均为11#、10#、6#风嘴,其中11#风嘴平台长度与风嘴角度均最大,即风嘴平台长度对于风嘴涡振制振能力的影响要大于风嘴角度的影响,增大风嘴平台长度能更为有效的提高风嘴的涡振制振能力。

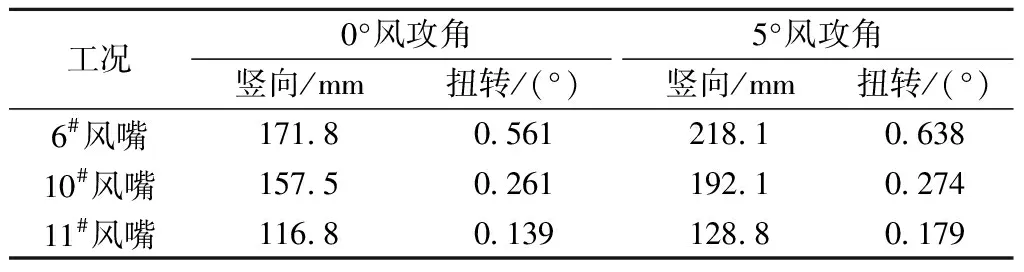
表8 6#、10#、11#风嘴工况最大涡振幅值

4 大比例尺节段模型涡振试验

大尺度节段模型通常采用比例尺为1∶15～1∶30,较1∶50～1∶70的小尺度模型,大尺度模型能够更为精细地模拟制作桥梁断面中对涡振特性较大的各类附属结构,且试验雷诺数与实桥值更为接近,从而能更为有效地反映梁体的实际涡振响应[26-30]。

综合之前得到的风嘴角度较小且平台长度较大的风嘴制振能力较好的结论,对加装了8#风嘴(总长度为4 m平台长度0.75 m)的主梁进行1∶25大比例尺节段模型风洞试验。试验在XNJD-3风洞中进行,试验段截面尺寸为22.5 m×4.5 m,主要试验参数见表9。

表9 1∶25节段模型试验参数

试验结果见图23,加装8#风嘴后,主梁仅在5°风攻角下发生涡激振动,其中最大竖弯涡振振幅仅为21 mm,最大扭转涡振振幅仅为0.028°,均远小于规范允许值。试验结果表明8#风嘴可以有效地抑制钝体钢箱梁在0°、±3°与±5°风攻角下的涡激振动。

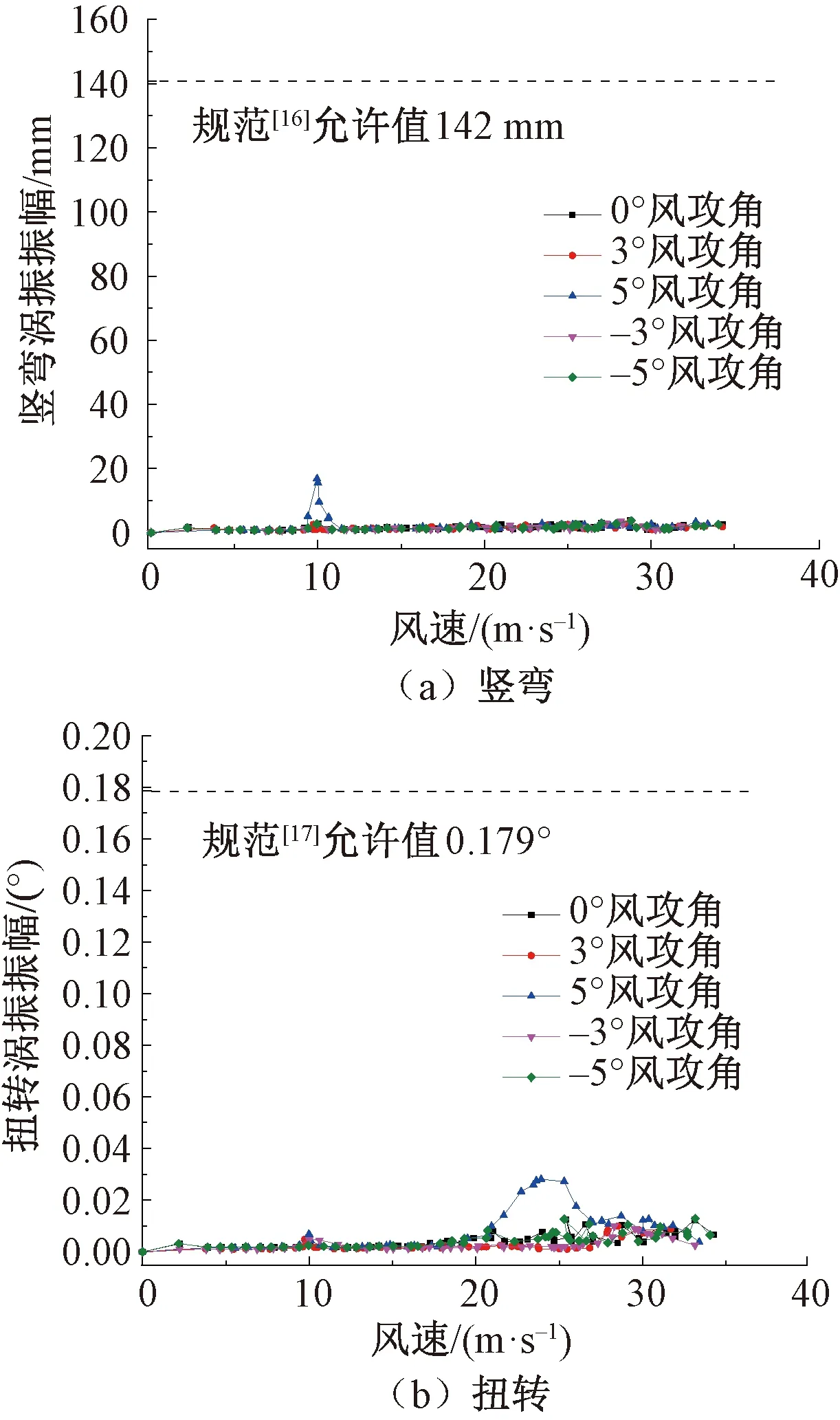
图23 加装8#风嘴断面主梁涡振响应

5 结论

基于本文涉及的节段模型风洞试验和数值模拟结果,得出主要结论如下:

(1)风嘴气动外形的改变对钝体铁路桥钢箱主梁的涡振响应影响显著,其中下行风嘴制振能力优于对称与上行风嘴,且随着风嘴角度的减小,风嘴的制振能力提高。

(2)在三角形风嘴上部设置平台可有效提高风嘴制振能力,且随着平台长度的增大,风嘴的制振能力提高。对于该类带平台的三角形风嘴,同时减小风嘴角度与提高平台长度可显著提高风嘴的制振能力,其中平台长度是主导影响因素。

(3)满足一定外形参数要求的带平台三角形下行风嘴(8#风嘴)可显著降低甚至消除钝体钢箱梁的涡激振动。

(4)CFD模拟结果表明,在钝体钢箱梁断面尾流区发生的大尺度卡门涡脱及由此产生的周期性气动力是导致涡激振动的主要原因,具有适当气动外形的风嘴能够有效改善该处的绕流状态及漩涡脱落尺寸,从而起到改善断面涡振性能的作用。