速度400 km/h高速列车风阻制动装置布置的数值研究
谢红太,王 红
(1.兰州交通大学 机电工程学院,甘肃 兰州 730070;2.华设设计集团股份有限公司 铁道规划设计研究院,江苏 南京 210014)
随着列车运行速度的提高,黏着制动力将逐渐降低,不能满足高性能制动需求,当列车在300 km/h以上速度等级运行时,所受空气阻力占总阻力的80%以上[1]。由此可见,现阶段在国内高速铁路全面提速的大背景和新一代更高速列车开展技术攻关以来[2-3],已经具备开发应用风阻制动装置的速度条件,尤其适合弥补列车在高速段制动时黏着制动力不足的问题,特别是在列车紧急制动情况下[4]。
国外,日本最早在宫崎试验线及山梨试验线上开展风阻制动装置在速度为500 km/h工况下MLU002 N型磁浮列车空气动力学计算和机构优化研究,并初步给出气动性能影响评估[1,5]。2005年6月,JR东日本公司联合开发了“猫耳”型空气动力制动装置[6],并于E954型[7]Fastech360 S和Fastech360 Z型高速列车成功安装应用[8],同时完成了速度400 km/h车况条件下的风阻制动板性能测试。试验结果显示,风阻制动装置在紧急制动时具有良好的可靠性和较高的应用价值。在风阻制动风翼板设计及安装布置方面,文献[9-10]重点对增大风阻制动装置阻力系数和缩小风阻制动装置体积两个主要方面的外形改造及布置进行了研究。
文献[11-12]在高速列车空气动力制动应用领域展开研究,参考日本的“猫耳”空气动力制动装置结构,分析列车顶部不同纵向距离、不同横向距离处制动风翼板阻力特性及外围流场分布情况。文献[13]通过列车空气动力学性能数值仿真方法,分析研究400 km/h带风翼板高速列车交会时的运行安全及可靠性。研究显示,与未开启制动风翼板相比其运行安全性指标均在合格范围内。文献[14-15]以矩形结构风翼板为研究对象展开研究,研究结果表明,高速列车纵向首排风翼板的高度变化对后排风翼板的流场干扰效应与制动力稳定性的影响较小。文献[16]采用计算流体动力学方法对带制动风翼板的高速列车分别从列车所受气动力、流场气动干扰效应及气动噪声等方面对首排制动风翼板不同纵向位置、不同迎风角度及不同组风翼板纵向布置做了详细计算说明,在此基础上分析计算了强侧风作用下带制动风翼板高速列车周围流场结构及气动力和力矩特性[17-18],同时对比不带制动风翼板高速列车,给出较为完善的成形及影响因素。
在制动风翼板结构设计及制造方面,国内外已研发了多种风阻制动装置[7-8,19],主要有日本早期研制开发的“猫耳”型风阻制动装置、分散式风阻制动装置及液压式风阻制动装置等。近年来,中车青岛四方车辆研究所有限公司公开了一种新型适用于速度400 km/h高速列车紧急制动工况的“蝶形”风阻制动装置[20-21]。上海庞丰机电科技有限公司公开了一种由纤维增强材料层夹泡沫夹心材料层设计构成的空气动力制动风翼板主体面板材料结构专利技术[22]。南京中车浦镇海泰制动设备有限公司公开了一种可以满足常用制动、紧急制动状态的不同需要、能实现风翼制动板0°~75°内任意角度锁定功能的高速列车风阻制动装置[23]。华设设计集团股份有限公司、兰州交通大学等提出一种基于不同迎风角度的可多级调控或无级调控的风阻制动装置,同时给出主辅风翼板配合制动的设计方案[24-26]。
从国内外风阻制动装置数值模拟仿真及实车上线试验研究来看,“猫耳”型风阻制动装置相对可提供较大的制动力,但其结构较复杂,质量大,收纳时会占用车厢大量空间。这对风阻装置小型化、轻量化提出了更为严峻的挑战。小型分散式风阻制动装置,一般采用两块风阻制动板互相抵消力矩的方式,该制动装置启动迅速,且收纳空间小,但在制动位时两块制动板存在一定的角度差,容易诱发旋涡气流以及颤振,对列车的运行安全性与稳定性有一定的影响。
就制动性能来看,国内主要以同济大学2014年在沪昆线(宜春至南昌西段)开展速度300、350 km/h的实车试验风阻装置,以及中车青岛四方车辆研究所有限公司2018年研究开发的“蝶形”风阻制动装置适用性及可行性表现较优,从高速列车运行平稳性及安全性方面考虑,“蝶形”风阻制动装置是目前较为优选的一种。但由于试验条件、不同车型的制动工况及车顶车内设备设施布置等因素限制,亟需进一步考虑多目标因素的高速列车风阻制动装置纵向布置及排数选择的方案和方法。本文以CR400AF平台动车组流线型外观为雏形,装配新型“蝶形”风阻制动装置[20],模拟计算高速列车不同布置状态时的气动特性,探索提出单排及多排制动风翼板布置的确定方法及最优方案。
1 计算模型
1.1 控制方程组
列车气动可归结为流体运动问题,而任何一个流场流动问题均可用非稳态的N-S方程描述[27-28]。
连续性方程
(1)
动量守恒方程
(2)
能量守衡方程
(3)
在对高速列车进行计算流体力学分析计算时采用三维定常可压黏性流场,其中外流场的湍流运动采用k-ε湍流方程模型[29],即湍动能方程和湍动能耗散率方程。
湍动能方程
(4)
湍动能耗散率方程
(5)
(6)
式中:ρ为流体密度;t为时间;p为静压力;τij为应力矢量分量;ρgi为i方向的重力分量;μl、μt分别为层流、湍流黏性系数;Fi=ρfi,为由于阻力和能源引起的其他能源项;h为熵;T为温度;kt是由于紊流传递而引起的传导率;Sh为定义的任何体积热源;ui、uj为流体沿i、j方向的速度分量;xi、xj为横坐标;Cμ、C1、C2、C3、σk、σε为系数,取值参考文献[30];Gk为由浮力产生的湍流动能;Gb为由层流速度梯度产生的湍流动能;k为湍动能;ε为湍动能耗散率;i、j为哑标。
采用有限体积法进行迭代求解,控制体积离散方程为
(7)
式中:t为时间;Γ为广义扩散系数;u为速度矢量;φ为流场通量;S为广义源项。
1.2 模型创建
1.2.1 高速列车及制动风翼板几何模型
(1)CR400AF平台标准动车组计算模型
CR400AF平台中国标准动车组为最高运营速度为350 km/h的动力分散式电动车组,动车组全列8辆编组,4动4拖,总长约208.95 m,车体最大宽度为3 360 mm。
在CFD仿真计算中参照文献[16]采用CR400AF平台中国标准动车组3辆编组1∶1实车常见几何模型,即头车、中间车及尾车连挂,其中头车车体长27.2 m,中间车体长25.0 m。
利用CATIA软件采用NURBS计算几何方法[31],依次完成CR400AF型动车组头车司机室流线型外观曲面的设计建模,其中k×l次的NURBS曲面可以表示为
(8)
式中:di,j为NURBS曲面控制点;m、n为取样点数;wi,j为与控制点di,j相对应的权因子;Ni,k(u)、Nj,l(v)分别为u向k次、v向l次的B样条基函数[32]。
为能够较为真实、快速地模拟高速列车在空气中的运行情况,在流体动力学仿真计算时模拟简化车底设备、转向架、车顶受电设备及风挡,同时忽略车侧门窗、把手等外部细节结构。创建3编组CR400AF平台动车组计算模型,如图1所示。几何模型全长77.2 m,其中车顶弧半径为12 000 mm,侧顶弧半径为800 mm。

图1 带制动风翼板CR400AF平台动车组模型
(2)风阻制动装置计算模型
新型“蝶形”风阻制动装置[33-34]主要包括前后反向开启的制动风翼板、主体框架基座、风翼板转轴、风翼板拉杆、滑动导轨、电机及其他控制、传感及传动电器组件等。整个制动装置横向对称嵌入安装于车顶内,风翼板表面曲面与车顶表面顶弧及侧顶弧面保持一致,厚度为100 mm,单块制动风翼板长宽尺寸为1 272 mm×378 mm,工作时开启角度为75°,其中制动风翼板迎风面垂向高度控制在365 mm,如图2所示。
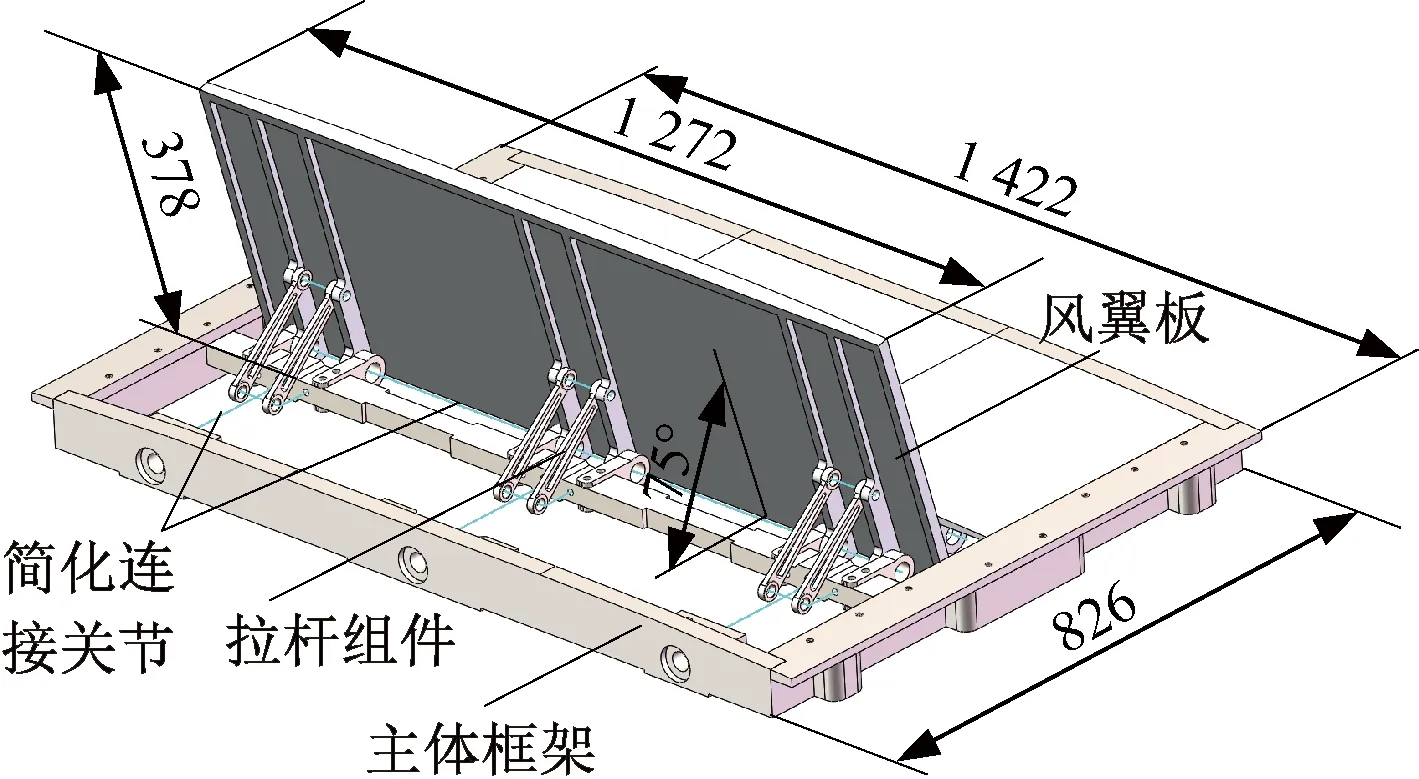
图2 风阻制动装置结构(单位:mm)
1.2.2 计算域设置
取全长为L的3编组CR400AF平台动车组几何模型,建立计算外流场模型,如图3所示。长方体外流场模型长×宽×高=4L×2L×L,其中,高速列车计算模型位于外流场模型两侧对称边界中部,列车底部距流场下壁面为0.3 m。
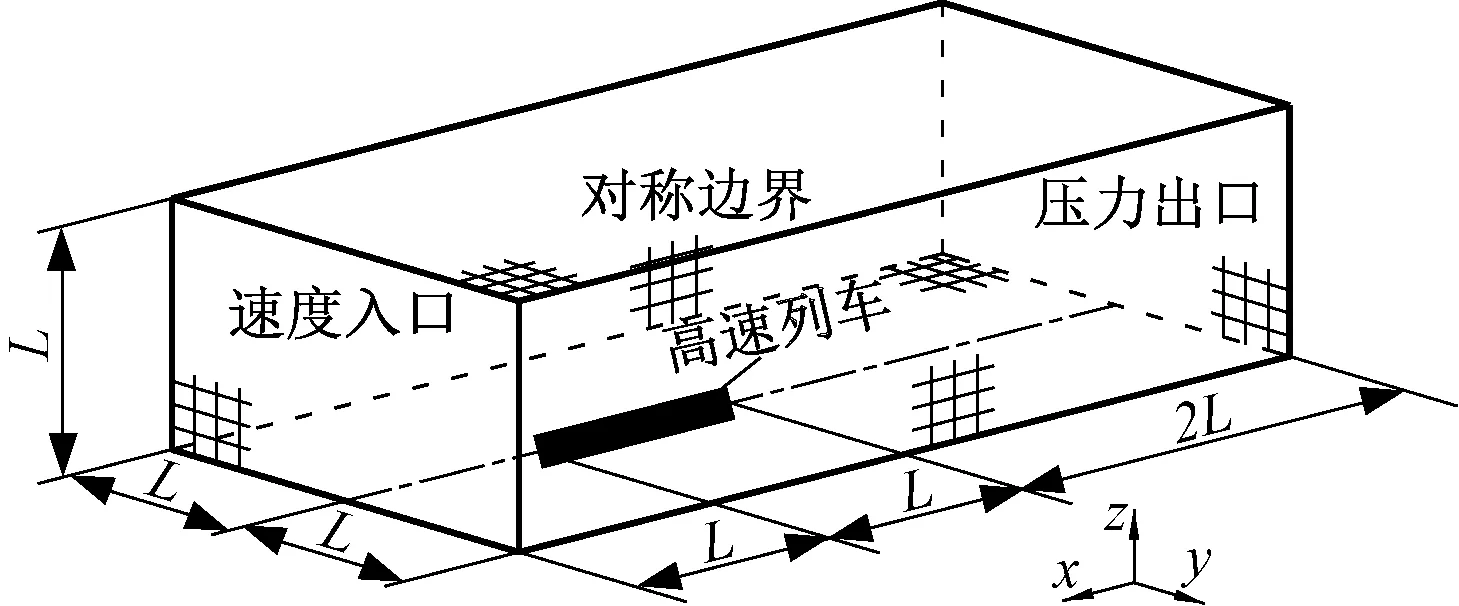
图3 计算区域及边界条件设置
出口边界条件设为压力出口,车体表面及制动风翼为无滑移壁面边界条件,外流场上表面和侧面设为无滑移光滑壁面边界条件,对称面设为对称边界,外流场下侧面(地面)设为移动壁面边界,移动速度的大小和方向与来流相同。
1.2.3 计算设置
计算区域网格采用基于曲率的六面体结构全局网格,采用ICEM进行网格划分,其中对于列车头尾部司机室及车顶制动风翼板外围流场变化突出的区域,设计采用全局和局部网格相配合叠加的处理模式,对称计算域结构网格总数约为335万个。
基于N-S及k-ε双方程湍流模型,采用有限体积法进行列车外流场的数值求解。
2 制动风翼板布置研究
根据Davis公式可知,运行列车所受总阻力可表示为机械阻力和气动阻力之和,其中气动阻力主要包括摩擦阻力和压差阻力,大小与速度平方成正比。根据计算流体力学类推计算,列车所受不同方向气动力可以表示为
FD=C1V2FL=C2V2FS=C3V2
(9)
式中:FD、FL、FS分别为纵向、垂向、横向气动力;C1、C2、C3分别为计算阻力系数、计算升力系数和计算横向力系数,与投影面积和流体密度成正比,其计算式为
C1=0.5ρADCDC2=0.5ρALCLC3=0.5ρASCS
(10)
其中,AD、AL、AS分别为纵向、垂向、横向方向投影面积,m2;ρ为空气密度,kg/m3,本文计算取ρ=1.205 kg/m3;CD、CL、CS分别为阻力系数、升力系数、横向力系数。
在列车空气动力学分析中常用阻力系数CD、升力系数CL和横向力系数CS分别表示列车所受空气阻力、升力和横向力的大小。根据式(9)、式(10)计算得
(11)
流体分析计算中,重点分析研究横向对称嵌入安装于车顶的新型“蝶形”风阻制动装置在纵向不同位置及不同布置数量时的气动特性,在忽略制动风翼板横向投影的情况下,带制动风翼板高速列车各向投影面积均为定值,即式(11)中列车纵向投影面积AD=12.477 m2,垂向投影面积AL=258.332 m2,横向投影面积AS=273.338 m2。
2.1 单排制动风翼板设置
高速列车流线型外观设计对外围空气流场结构影响较大,对于降低列车运行空气阻力及气动噪声有重要影响。由式(11)可知,在一定速度等级条件下运行时,列车所受空气阻力与其纵向投影面积成正比,同时依据“蝶形”风阻制动装置于车顶对称安装布置要求,纵向n排制动风翼板投影面积相同的条件下,根据列车外围流场成形及分布范围进行合理确定单排制动风翼板的纵向安装位置是尤为重要的。
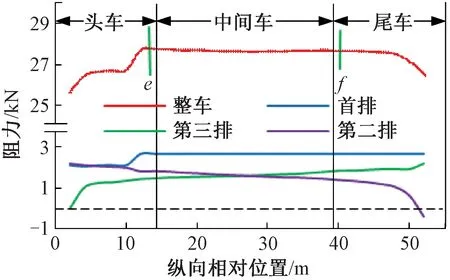
为保证高速列车头车流线型设计同时考虑制动风翼板的安放空间需求,高速列车单排制动风翼板安放位置一般选择在头车司机室前端流线型尾端连接处以后部位[16],本文分析计算中记风翼板安装位置至司机室前端流线型尾端连接处纵向距离为xd(0≤xd≤Ld,Ld=55.4 m),Ld为头车司机室流线型尾端连接处至尾车间司机室流线型尾端连接处的纵向距离,以制动风翼板所受纵向阻力为研究对象,取xd=0、2、4、…、54、56、57.4 m处30个安装位置,来流速度v=400 km/h,分别进行流体动力学计算,所受阻力如图4所示。
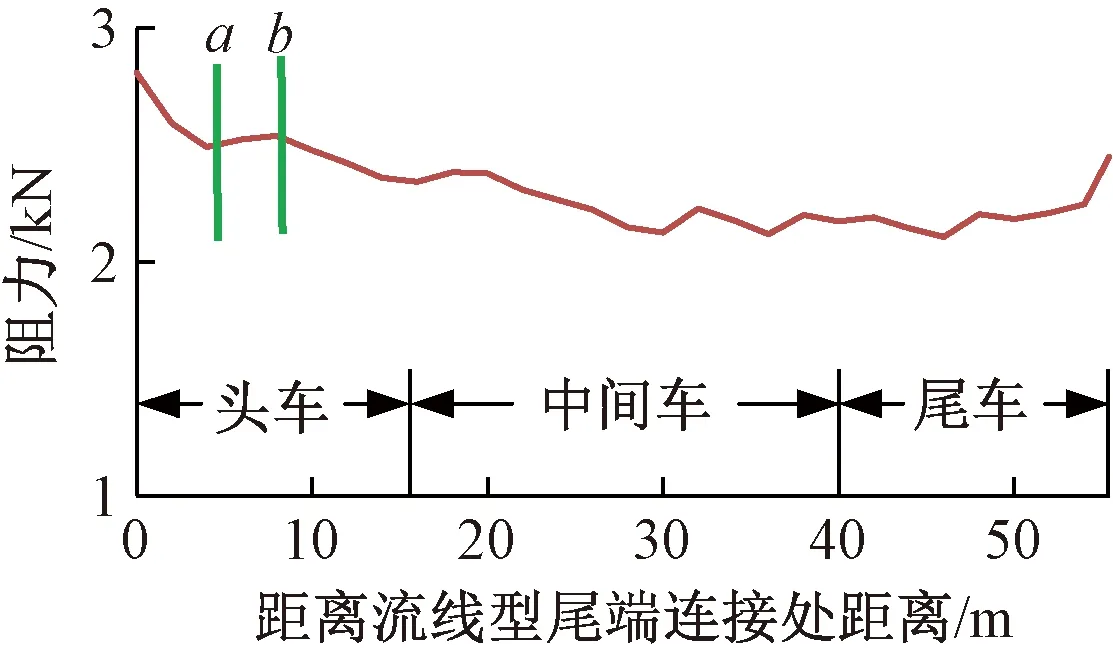
图4 单排制动风翼板纵向布置阻力变化趋势
由图4可知,随着制动风翼板安装位置至司机室前端流线型尾端连接处纵向距离xd的逐渐增大,风翼板所受纵向阻力整体于头车顶范围内呈迅速下降趋势,并于中间车车顶范围逐渐趋缓,最后在尾车车顶范围内逐渐增大,于尾车司机室前端流线型尾端连接处达到最大。其中头车及尾车司机室前端流线型尾端连接处局部范围作为车头与车身的过渡段,由于曲面设计曲率大,造成此处气流流速快,形成较大负压区,因此,出现了该区域内纵向制动风翼板所受纵向阻力较大且变化快的现象。
为进一步研究车顶不同位置处所安装制动风翼板气动特性,选取列车头车司机室前端流线型尾端连接处至尾车司机室前端流线型尾端连接处车顶纵向中心线以上200 mm处空间虚拟线位置,分别提取xd=0、4、8、…、52、55.4 m处共15个布置状态时速度和静压纵向分布情况,如图5所示。
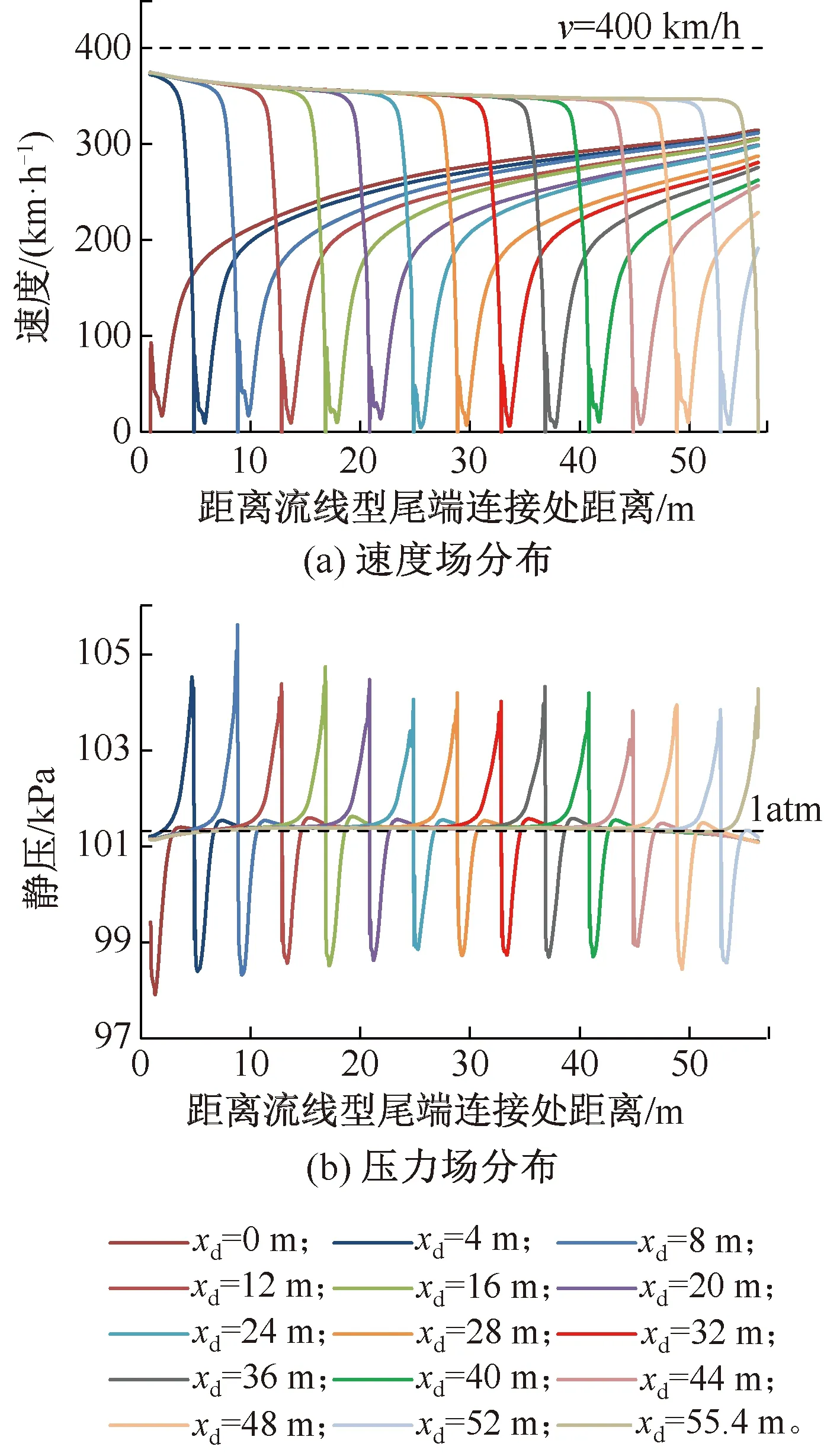
图5 车顶纵向中心线以上200mm处参数研究
经模拟计算分析结合已研究成果[4,35],首排制动风翼板在高速列车头车司机室前端流线型尾端连接处后xd=[0,2]m范围内,首排制动风翼板在司机室顶部巨大负压区的影响下,受力达到最大,随着纵向安装位置后移,受力迅速减小。xd=[2,5]m范围内受力基本相当,相比头车司机室前端流线型尾端连接处产生的最大阻力Fdmax(xd=0 m)=2 810.65 N,减小10.19%。xd=[0,2]m范围内考虑气动噪声、瞬态冲击下风翼板结构振动及对头车流线型设计影响等综合分析,本文给出单排制动风翼在高速列车头车布置的优选位置为高速列车头车司机室前端流线型尾端连接处以后xd=[2,5]m范围内,该范围内可有效为高速制动阶段列车提供可靠稳定的制动力。
基于此,为充分对比研究单排制动风翼板对高速列车气动特性影响,分别在不同速度等级下对不带风翼板和带首排制动风翼板高速列车所受纵向阻力和垂向升力进行计算分析(取xd=3.0 m),如图6所示。理论条件下,数值模拟计算中列车所受横向力为0。

图6 不同速度等级条件下列车所受阻力及升力
根据式( 9 )~式(11)分别计算带制动风翼板和不带制动风翼板高速列车整车、头车、中间车及尾车阻力系数CD及升力系数CL,见表1。
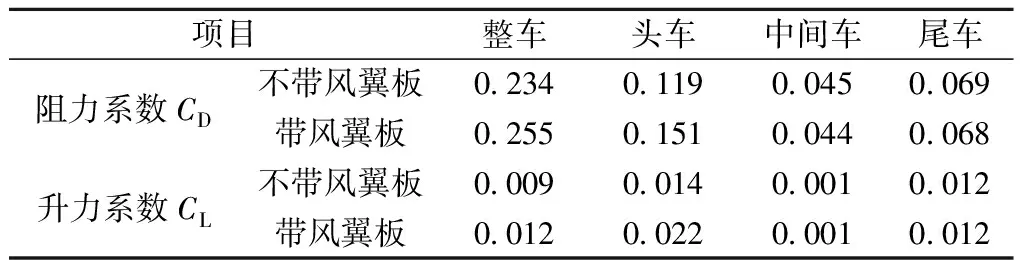
表1 带制动风翼板高速列车模拟对比计算结果
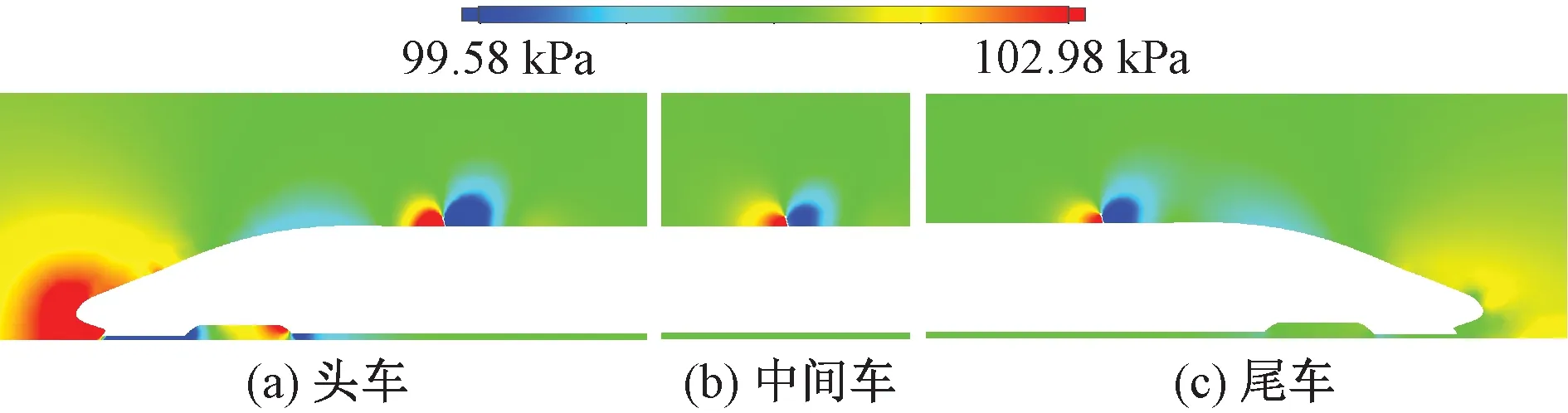
由图6可知,在不同速度等级下不带风翼板和带首排风翼板高速列车所受纵向阻力和垂向升力均与速度的平方成正比,分别以整车、头车、中间车及尾车为研究对象进行对比分析。可以看出,带风翼板列车整车及头车所受纵向阻力FD及垂向升力FL较不带风翼板列车均有大幅增加。由表1可知,因首排制动风翼板安装整车阻力系数CD从0.234增大至0.255,升力系数CL从0.009增大至0.012,中间车及尾车因受风翼板影响较小,基本保持不变。当V=400 km/h时,头车所受阻力增大约31.63%,升力增大约60.77%,整车所受阻力增大约13.99%,升力增大约30.27%;带制动风翼板列车所受阻力中头车、中间车及尾车分别占比为58.97%、16.41%、25.52%,所受升力分别占比为51.07%、3.33%、45.60%。
2.2 多排制动风翼板设置
2.1节对单排制动风翼板设置研究表明,制动风翼板的安装进一步增加了列车外围流场结构的复杂性,同时对范围内该节车辆阻力及升力变化影响较大,因此如何科学合理的根据运用需求有效布置多排制动风翼板是目前需要解决的一个问题。
由式(11)可知,高速列车所受纵向空气阻力FD=0.5ρADV2CD,n(n≥2)排制动风翼板布置时,根据本文“蝶形”风阻制动装置横向对称嵌入安装于车顶沿纵向中线不同位置布置的形式,沿列车运行方向后序制动风翼板对前序风翼板外围流场形成存在干扰,在选定首排制动风翼板情况下(阻力系数表示为CD0),引入第i排风翼板直接干涉系数CD1(i),则高速列车所受纵向空气阻力FD可表示为
(12)
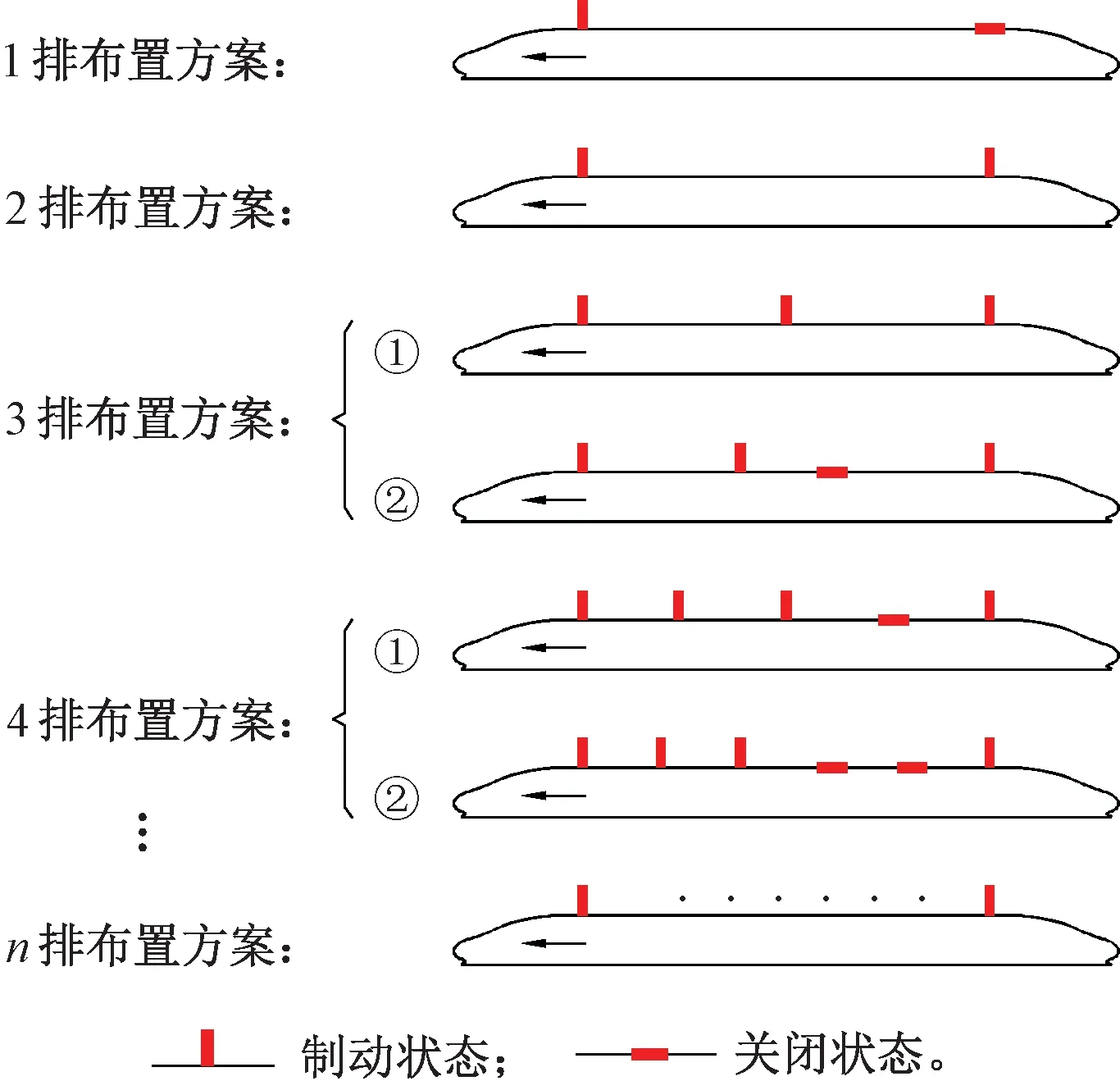
以高速列车制动需求为目标,采用纵向制动风翼板最优范围布置逐渐递增的方式,通过计算流体力学方法确定高速列车制动风翼板设置位置及布置排数选择,计算方法流程如图7所示。

图7 高速列车制动风翼板设置位置及布置排数选择流程
2.2.1 2排制动风翼板设置
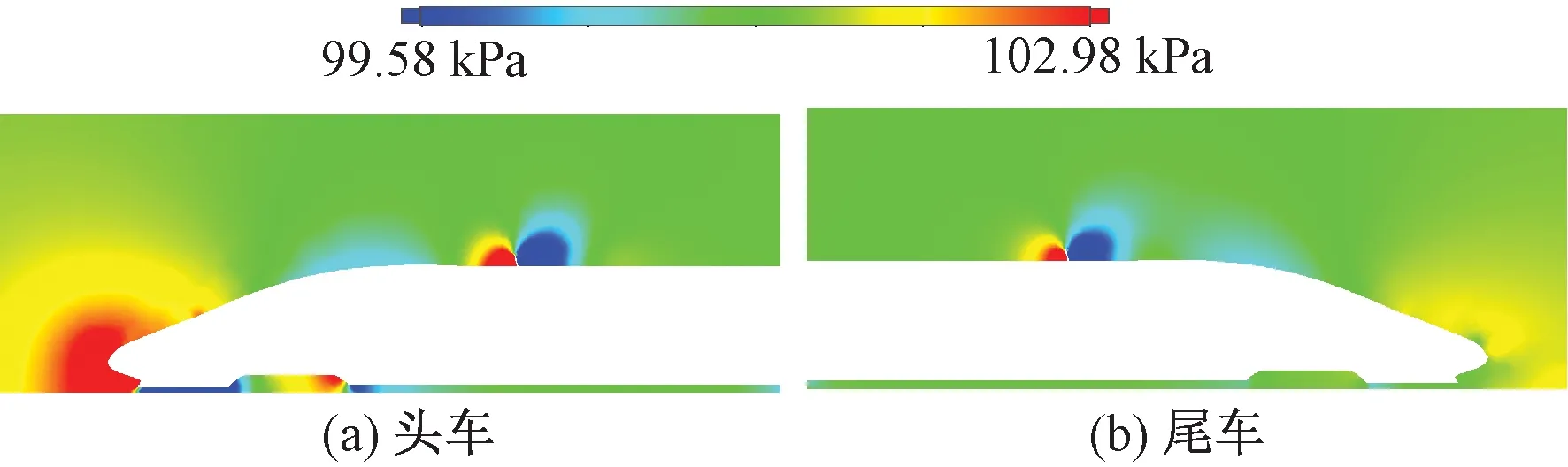
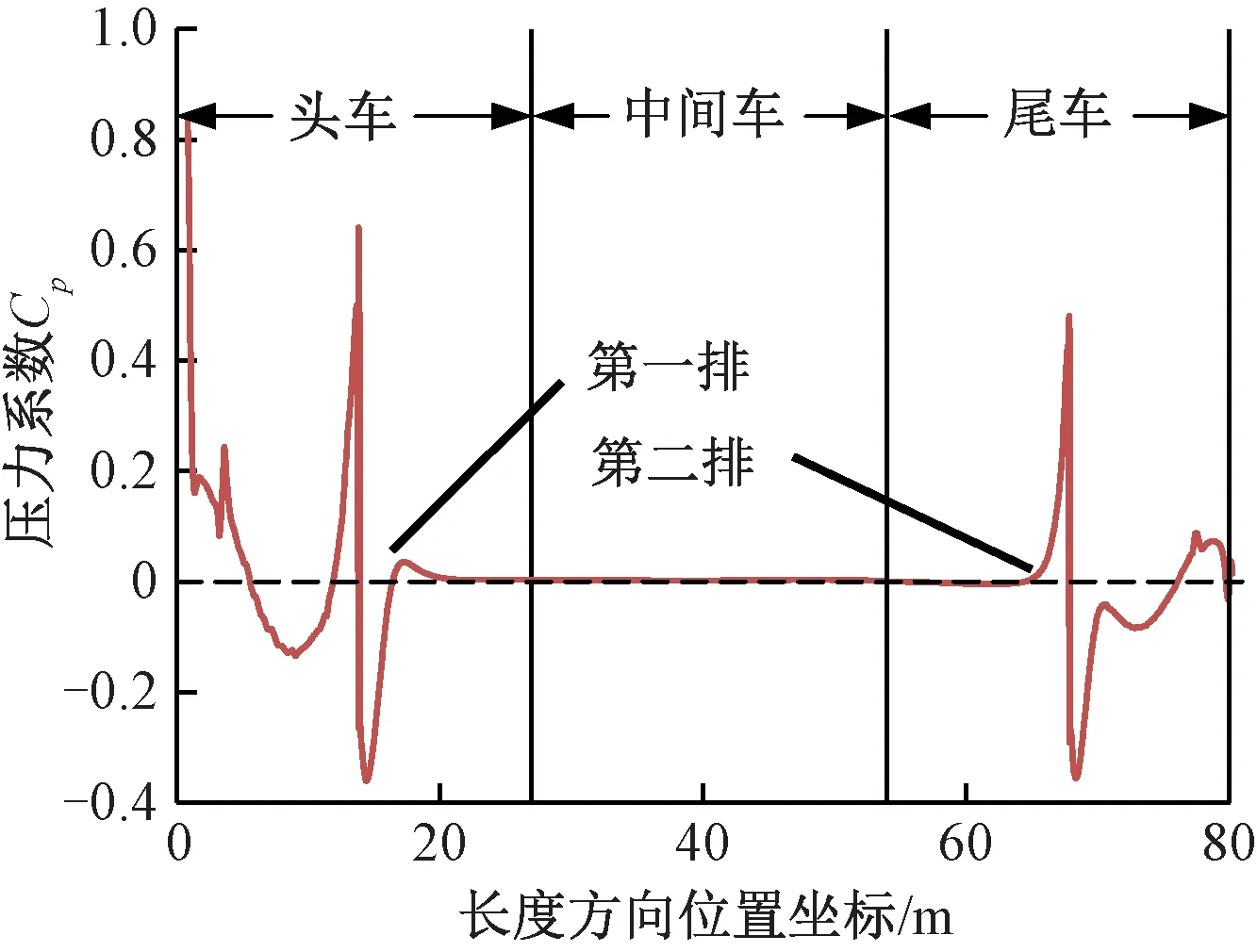
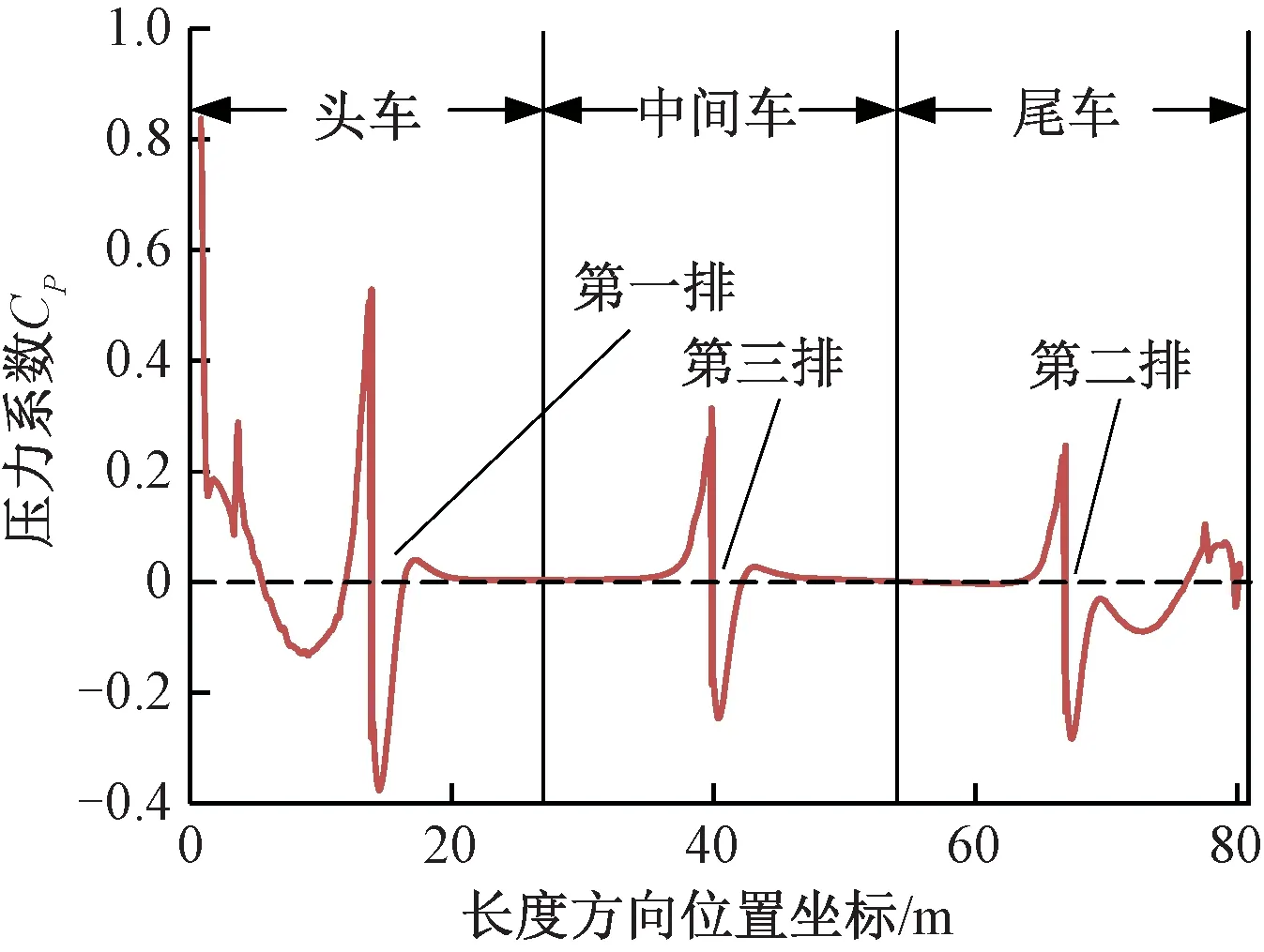
在2.1节首排制动风翼板安装位置设置的基础上(高速列车头车司机室前端流线型尾端连接处后[a,b]范围内取最优点xd=3 m处),记第2排风翼板安装位置至首排制动风翼板安装中心位置纵向距离为xs(0 图8 2排制动风翼板纵向布置阻力变化趋势 由图8可知,2排风翼板布置时产生总阻力呈逐渐上升趋势,其中第1排制动风翼板所产生的阻力在xs=[0,3]m范围内由于受第2排制动风翼板影响,两风翼板之间形成1个比较明显的涡系,随着距首排制动风翼板中心位置距离xs的增大而逐渐减弱消失,导致局部范围内第1排制动风翼板所受阻力出现降低后再恢复,并逐渐保持平稳。第2排制动风翼板所受阻力在xs=[0,2.5]m范围内受反向阻力作用,随着距首排制动风翼板中心位置距离xs的增大阻力逐渐增加,整体小于单排布置时产生的阻力值。 经计算流体力学分析研究,在头车司机室前端流线型尾端连接处后xd=3 m处设置首排风翼板,选定后,2排制动风翼板布置时,第2排风翼板设置在尾车司机室流线型尾端连接处后部范围内所受阻力达到最大,结合高速列车双向运行特点及首排风翼板位置选择,2排布置时选取首排布置时优选范围[a,b]对应纵向对称位置范围[c,d]。计算中最优点取xs=51 m,根据式(12)得第2排风翼板直接干涉系数CD1(2)=1.09,其中v=400 km/h时,列车所受空气阻力FD=25.87 kN,较单排制动风翼板布置增大约9.10%。 2排制动风翼板安装布置时,头车及尾车纵向对称面上车身外围压力场分布如图9所示。 图9 2排制动风翼板纵向布置时车身外围压力场分布 提取带制动风翼板列车纵向对称面上部外流场与列车截面接触线,参照文献[17]分别在计算模型长度方向以头车尾车导流罩前鼻锥滞止点为计算起点和终点参考点,根据压力系数Cp=(p-p∞)/(0.5ρV2)(其中,p为计算点静压;p∞计算域远环境压力,此处为标准大气压)计算纵向对称面上部外流场与列车截面接触线上压力系数分布,如图10所示。 图10 2排制动风翼板布置时列车纵向对称面上部接触线压力系数 2.2.2 3排制动风翼板设置 同理在2排制动风翼板安装位置设置的基础上(首排制动风翼板安装位置为高速列车头车司机室前端流线型尾端连接处后[a,b]范围内取最优点xd=3 m处,第2排制动风翼板安装位置为距首排制动风翼板中心位置距离xs=51 m处),记第3排风翼板安装位置至第首排制动风翼板安装中心位置纵向距离为xz(0 图11 3排制动风翼板纵向布置阻力变化趋势 由图11可知,3排风翼板布置时整车阻力在xz=[0,4]m范围内,由于第3排风翼板距离首排风翼板纵向距离加大,两风翼板之间区域形成的涡系逐渐减弱、正压增强,所产生的空气阻力迅速增加。xz=[4,12.5]m范围内,随着第3排制动风翼板对首排制动风翼板流动干扰效应的进一步减弱,约xz=10 m后干扰效应逐渐消失,整车所产生的空气阻力突增至27.79 kN,首排所产生的空气阻力突增至2.68 kN。xz=[12.5,45]m范围内,随着第3排制动风翼板位置的后移,首排风翼板后部空气流速加大,第3排制动风翼板所受空气阻力逐步增加,相反,第2排制动风翼板所受空阻力逐渐减小,整车阻力基本维持平稳。xz=[45,51]m范围内,随着第3排和第2排风翼板之间距离缩小,板间范围内涡系逐渐形成并增强、负压增强,导致第3排风翼板所产生的空气阻力有微增趋势,第2排风翼板所产生的空气阻力迅速减小,直至进一步逼近而产生负阻力,整车所受空气阻力随xz的增加而减小。 3排制动风翼板安装布置时,头车、中间车及尾车纵向对称面上车身外围压力场分布如图12所示。 图12 3排制动风翼板纵向布置时车身外围压力场分布 计算纵向对称面上部外流场与列车截面接触线上压力系数分布,如图13所示。 图13 3排制动风翼板布置时列车纵向对称面上部接触线压力系数 2.2.3n排制动风翼板设置 以高速列车制动需求为目标,采取纵向制动风翼板最优范围布置逐渐递增的方式,根据高速列车不同车型技术标准、运行线路条件及列车空气制动需求等技术参数,同时结合列车双向运行特点、车顶受电弓及车内设备空间布局等因素,通过计算流体力学的方法确定高速列车多排制动风翼板设置位置及布置排数选择方案如图14所示。 图14 多排制动风翼板布置方案示意 基于计算流体力学方法,分析研究“蝶形”风阻制动装置在纵向不同位置及不同布置数量时的气动特性,给出首排及多排制动风翼板纵向确定方法及最优方案。研究结论如下: (1)在高速列车头车司机室前端流线型尾端连接处后2~5 m范围内,设置安装首排制动风翼板可有效对列车高速运行制动阶段提供较为可靠稳定的制动力。当列车以速度400 km/h运行时头车所受阻力增大约31.63%,升力增大约60.77%,整车所受阻力增大约13.99%,升力增大约30.27%。 (2)提出以高速列车制动需求为目标,纵向制动风翼板最优范围布置逐渐递增的方式,通过计算流体力学方法确定高速列车制动风翼板设置位置及布置排数选择的研究方法,同时计算给出3节编组高速列车2排及3排制动风翼板最优布置方案范围。当2排布置时,均设置在头车及尾车司机室前端流线型尾端连接处后优选稳定[2,5]m范围中的3 m处,后排风翼板直接干涉系数为1.09。速度400 km/h制动时列车所受空气阻力较单排制动风翼板布置增大约9.10%;当3排布置时,在2排布置的基础上,计算最优点为中间车车顶纵向中心点处,直接干涉系数为1.17,速度400 km/h制动时列车所受空气阻力较首排和2排制动风翼板布置分别增大约16.70%、6.96%。 (3)在风阻制动风翼板于列车车顶纵向位置选择中,提出考虑既有车顶及车内设备布局和双向制动需求等多目标的多排制动风翼板的布置优化方法,本文研究暂未直接引入纵向影响因素。基于此,下阶段应根据具体车型实际考虑车顶及车内设备布局的情况下,合理细化风翼板制动系统的布置方案,同时应结合试验样机进一步研究风阻制动的标准试验方法,特别是不同装置位置及运行工况的地面风载荷试验和线路试验模拟方法,以及试验结果的评价标准。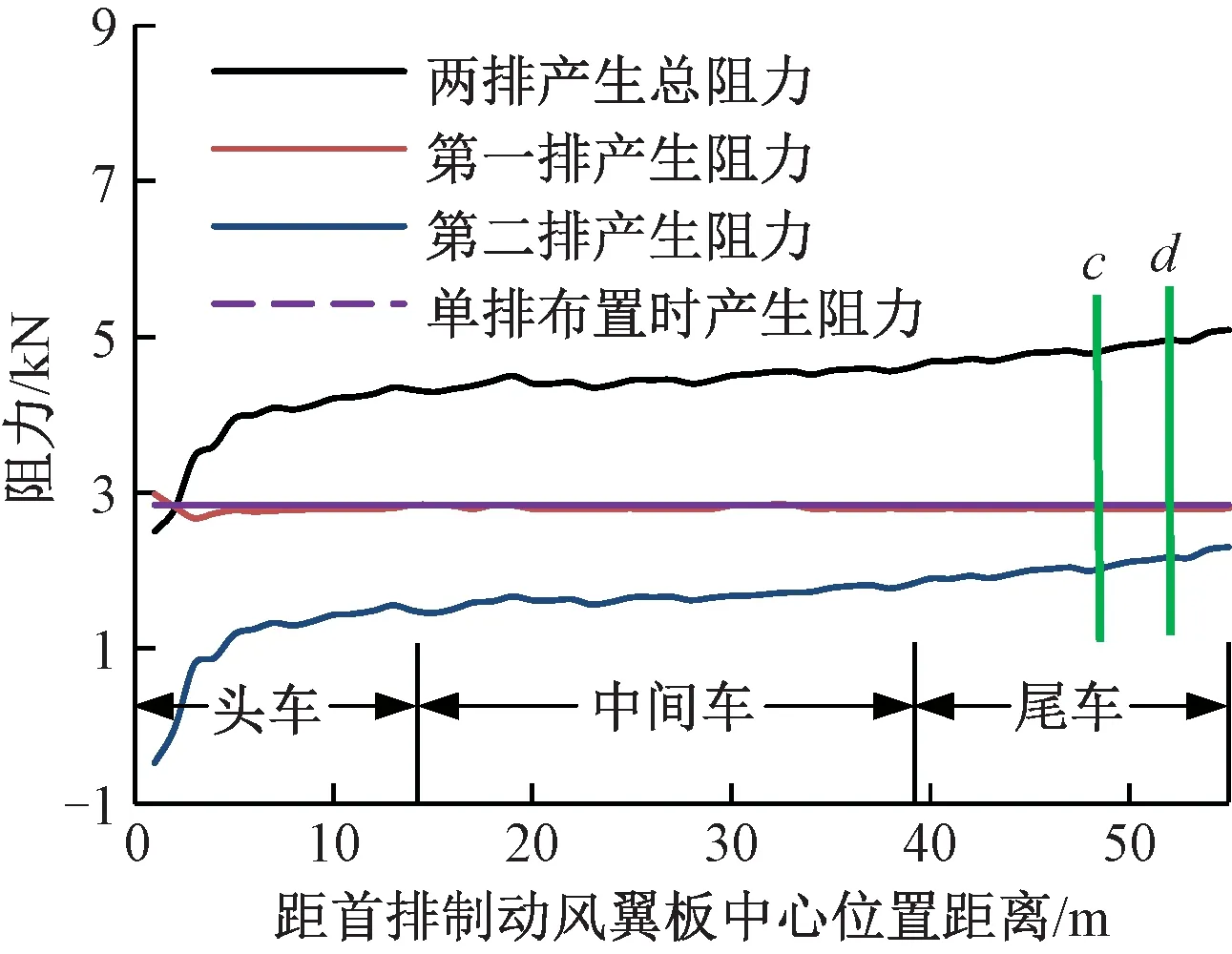
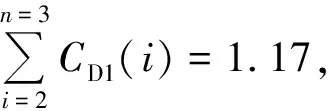
3 结论

