基于BP神经网络的转向架斜楔参数优化
刘嘉兴,吕大立,3,吕可维,张琪昌,李玉龙
(1.天津大学 机械工程学院,天津 300072;2.天津市非线性动力学与控制重点实验室,天津 300072;3.天津大学 内燃机研究所,天津 300072;4.中车齐齐哈尔车辆有限公司 大连研发中心,辽宁 大连 116042)
斜楔减振器是铁路货车转向架的重要元件,对转向架以及整个车体的减振性能有重要影响[1]。文献[2]指出,转向架斜楔产生的卡滞现象是当前转向架优化设计研究中迫切需要解决的问题,确定斜楔参数的最优配置是解决卡滞问题的重要途径。然而如何去确定合适的斜楔参数是一个需要解决的问题,文献[3-4]研究已经表明斜楔摩擦系数对货车动力学性能影响的复杂性。因此,采用传统解析方法,推导斜楔参数与车体响应的解析关系式,再根据解析关系式对斜楔参数进行优化是难以实现的。
针对上述问题,本文采用数据驱动[5]的方法建立斜楔参数与车体响应关系模型,根据建立的关系模型对斜楔进行优化。采用该方法对斜楔进行参数优化,需要大量的准确数据做支撑。由于货车系统庞大且复杂,较难通过实验获得不同斜楔参数下的车体响应数据,因此本文通过准确的货车仿真模型获得所需数据。
随着近年来刚柔耦合多体动力学的发展,越来越多学者的研究表明货车部件柔性对货车动力学性能有较大影响[6-8]。因此为了保证货车模型的准确性,本文建立货车刚柔耦合多体动力学模型计算不同斜楔参数下的车体响应。为了保证不同斜楔参数下的车体响应数据准确且满足数量要求,应确保斜楔部分的建模能准确反映斜楔作用,且易于更改斜楔参数。
由于斜楔与转向架其他部件摇枕、侧架等相比质量较小,通常被处理成一个简单力元。传统方法采用相对摩擦系数φ建立摩擦力元等效替代斜楔的作用,其定义为转向架加载和减振过程中,斜楔主摩擦面摩擦力的平均值与中央悬挂弹簧垂向力的比值[9],即
(1)
式中:fl为转向架加载时斜楔主摩擦面摩擦力;fu为转向架减载时斜楔主摩擦面摩擦力;Pz为转向架中央悬挂所有弹簧垂向力的合力。
采用相对摩擦系数法可以描述斜楔的减振作用,获得一个相对准确的转向架动力学模型,且采用该方法处理斜楔复杂度低,因此近年来仍有学者采用该方法处理斜楔[6,10]。然而相对摩擦系数法只考虑了斜楔的垂向作用,斜楔纵向、横向以及抗菱作用并未考虑,且该方法只能反映斜楔在一个加减载循环内的垂向摩擦作用,并不能反映斜楔实时的摩擦作用。针对上述问题,文献[11]在ADAMS软件中建立斜楔实体模型,利用固定在斜楔体上的4个小球建立斜楔的接触关系。文献[9]在Simpack软件中建立可以分析斜楔多向动态作用的斜楔实体模型,计算结果与试验有较好的吻合度。文献[12-13]在UM中建立斜楔的实体模型,斜楔与侧架的接触区域用4个角点坐标来描述。
与相对摩擦系数方法相比,建立斜楔实体模型模拟斜楔作用,模型准确度更高。然而由于模型复杂度高,斜楔形状尺寸的变动都需要对模型进行一定程度的更改,因此不利于计算不同斜楔参数下的车体响应,尤其是考虑转向架柔性时,将进一步增加建立斜楔实体模型的复杂程度。
综上,相对摩擦系数法简便,但无法反映斜楔多向作用;斜楔实体模型方法可以准确模拟斜楔作用,但模型相对复杂,不利于计算不同斜楔参数下的车体响应。因此采用等效作用力元的方法模拟斜楔作用,使模型能准确反映斜楔多向作用,同时便于计算不同斜楔参数下的车体响应。以转K6转向架为研究对象,在垂向、横向、纵向及抗菱作用上对斜楔进行受力分析,分析斜楔各向的等效作用,建立斜楔各个方向上的等效参数力元模拟斜楔作用;进一步在Simpack软件中建立便于优化斜楔主摩擦系数、副摩擦系数及斜楔角度,同时考虑车体、侧架、摇枕柔性的C70E刚柔耦合货车整车多体动力学模型。
利用上述货车整车多体动力学模型,计算不同斜楔参数下的车体加速度响应,采用遗传算法优化的BP神经网络建立斜楔参数与车体加速度响应的关系模型,并以此关系模型为适应度函数,并利用遗传算法对斜楔参数进行优化,寻找在一定合理参数范围内使货车车体加速度响应最小的斜楔参数。
1 斜楔等效作用力学分析
1.1 模型简介
转K6转向架模型如图1所示,斜楔与侧架的接触面为主摩擦面,与水平面垂直;斜楔与摇枕的接触面为副摩擦面;斜楔角度α为副摩擦面与斜楔底面的夹角。由于货车运行时斜楔与侧架、摇枕的接触区域变形量与三者位移相比较小,因此在力学分析过程中,假定斜楔、侧架与摇枕均为刚体,斜楔与摇枕侧面无间隙。
1.2 垂向作用
当摇枕上存在垂向预加载力FC0及垂向力FC1作用时,转向架及斜楔受力如图2所示。垂向力FC1方向向下时,转向架为加载状态,摇枕速度v为正。当主摩擦面与水平面垂直,斜楔副摩擦面仅在斜楔运动方向改变时存在摩擦力[9]。因此垂向运动时,斜楔受力如图2左侧所示,图中μ1为主摩擦面摩擦系数,FP为斜楔弹簧力,FR1为侧架对斜楔的压力,FN1为摇枕对斜楔的正压力。

图2 转向架垂向受力
由图2可知,在转向架垂向加载或减载过程中,斜楔减振器在垂向提供了斜楔弹簧力FP和主摩擦面摩擦力fc的作用,fc可以表示为
(2)
式中:sign为符号函数。同时为了在模型中反映斜楔变向时的摩擦力作用,斜楔摩擦力fcz为
(3)
式中:f0为静摩擦力,在Simpack中由斜楔与侧架的速度和受力状态判定;veps为判断斜楔是否滑动的速度条件,在Simpack中一般设为0.001 m/s。
1.3 横向作用
当转向架仅在水平面发生横向运动时,转向架受力如图3所示。在转向架横向运动过程中,斜楔在横向仅提供了斜楔弹簧横向力FPH及主摩擦面横向摩擦力FRH的作用。在Simpack中FPH可由斜楔弹簧横向刚度设定;横向摩擦力FRH可由垂向摩擦力公式(3),根据斜楔垂向和横向的速度进行正交分解[9]得到。

图3 转向架横向受力
1.4 纵向作用
当斜楔弹簧预压缩量为f,摇枕发生纵向位移x时,转向架受力如图4所示。FQ1和FQ2分别表示前后斜楔弹簧所提供的力;当摇枕发生纵向位移x时,斜楔的垂向位移为h。斜楔在摇枕纵向加载过程中提供纵向等效刚度的作用。
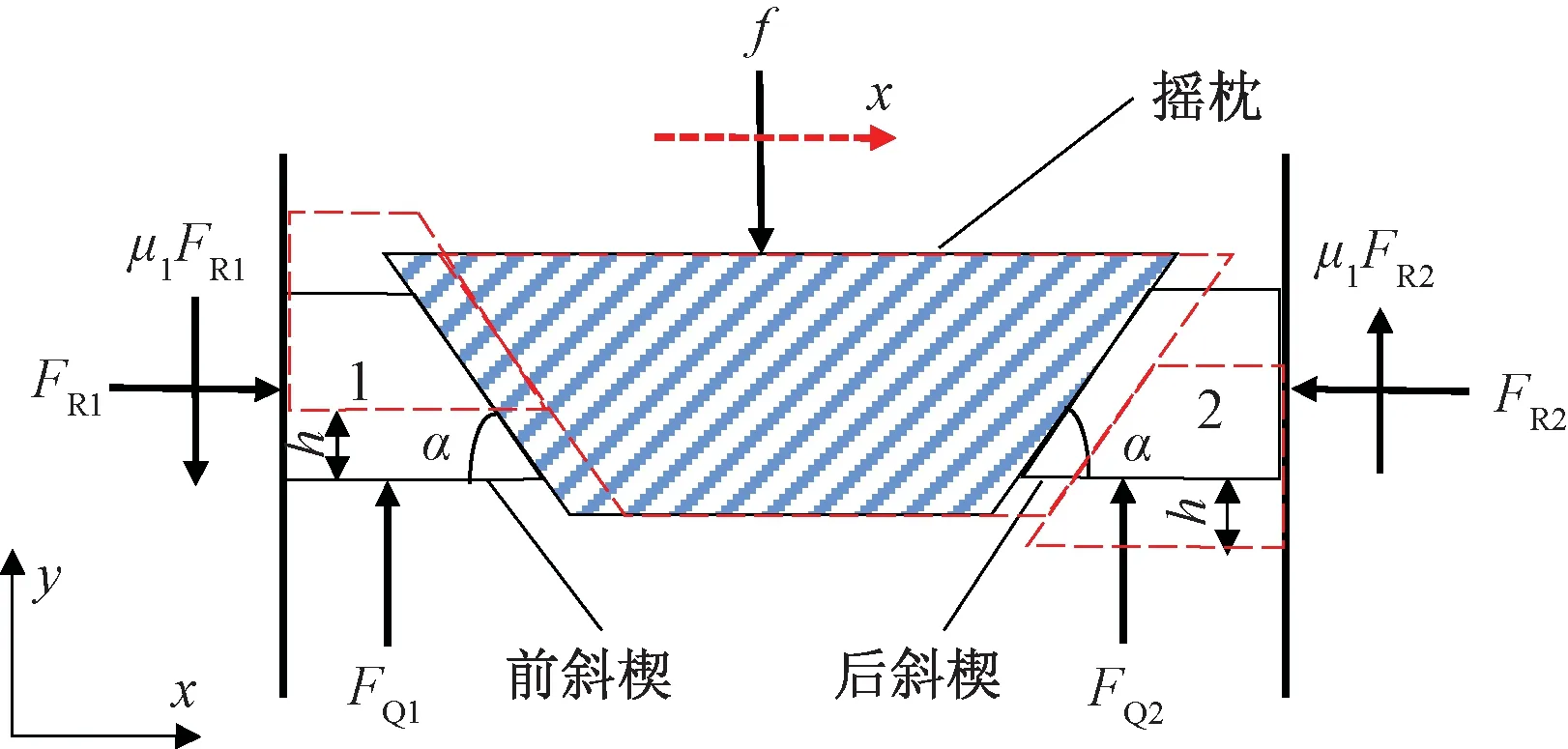
图4 转向架纵向受力
分别对前后斜楔进行受力分析,再对转向架整体进行纵向受力分析,可以得到斜楔提供的摇枕纵向力Fz与摇枕位移x之间的关系,Fz对x求导可以得到斜楔提供的纵向等效刚度kz为
(4)
式中:ks为斜楔弹簧垂向刚度;μ2为副摩擦面摩擦系数。
1.5 抗菱作用
当转向架发生菱形变形时,如图5所示,摇枕与侧架的相对位置由垂直变为倾斜,侧架宽度为L不变,摇枕与斜楔的纵向宽度变窄,两斜楔被挤向摇枕中央,斜楔沿副摩擦面向下运动,当侧架相对摇枕转动角度θ时,两斜楔作用于侧架的力F1在侧架中心产生的力矩M,即斜楔在转向架发生菱形变形时对侧架提供的力矩作用[14]。
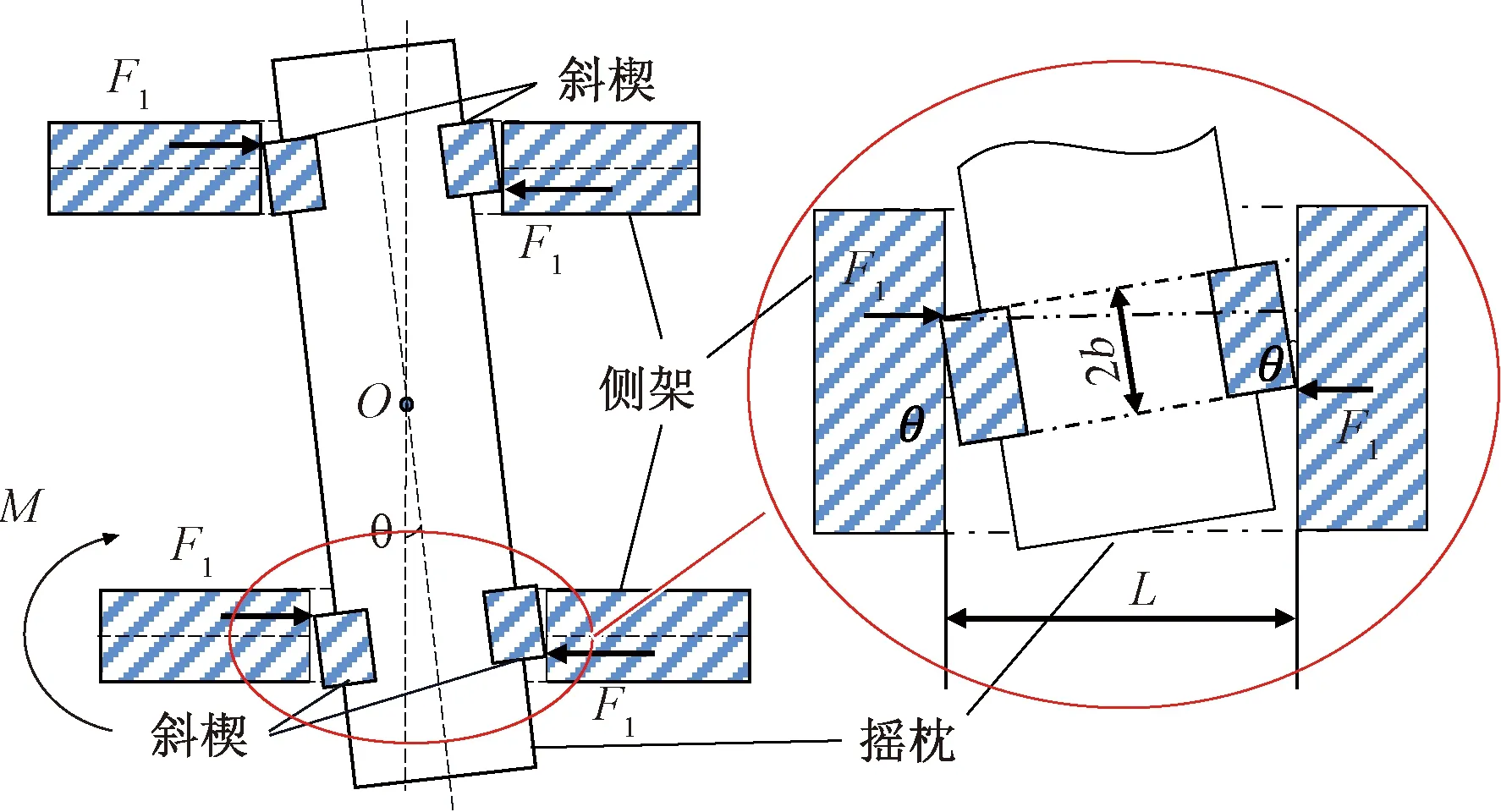
图5 转向架抗菱受力
对斜楔进行受力分析,再对转向架整体进行受力分析,得到斜楔对侧架提供的力矩M和侧架转角θ之间的关系,M对θ求导可得斜楔提供的抗菱刚度kL为
(5)
式中:b为斜楔纵向宽度的一半。
2 货车刚柔耦合模型
2.1 模型的建立
当车辆高速运行时,车辆部件的柔性作用对车辆动力学性能有重要影响。因此,为了准确描述货车的动力学性能,建立考虑转向架及车体柔性的C70E货车刚柔耦合模型,建模流程如图6所示。根据C70E货车参数[6],在有限元软件中建立车体、转向架部件侧架与摇枕的有限元模型,对车体、摇枕以及侧架进行模态分析和子结构分析,将计算好的相关文件通过Simpack的FEMBS接口程序生成弹性体标准输入文件,并导入Simpack中,生成车体、摇枕及侧架的柔性体模型,同时在Simpack中建立其他不考虑柔性的刚体部件模型,建立好的C70E货车刚柔耦合整车模型如图7所示,其中货车车体、摇枕、侧架为柔性体,轮对为刚体。
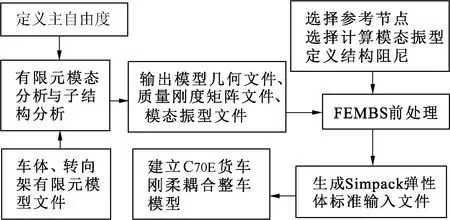
图6 刚柔耦合模型建模流程

图7 C70E货车刚柔耦合模型
在建立好的C70E货车刚柔耦合整车模型的基础上,采用本文提出的斜楔等效作用法对斜楔进行建模处理,参照如下步骤进行设置:将斜楔角度、主摩擦系数、副摩擦系数、斜楔弹簧刚度及斜楔纵向宽度,代入斜楔垂向、横向、纵向及抗菱作用解析式(2)~式(5),在Simpack中建立斜楔等效摩擦力元及等效刚度力元模拟斜楔作用。
2.2 模型验证
为了确保刚柔耦合货车模型上对斜楔参数进行优化的精度满足要求,对建立的C70E货车刚柔耦合模型进行验证。
通过对比货车模型的模态振型频率和非线性临界速度验证模型的准确性,C70E货车刚柔耦合模型,是根据文献[6]中的C70E货车参数建立而成的,因此将通过Simpack多体动力学软件,计算本文建立的C70E货车刚柔耦合模型的模态振型,并将计算得到的模态振型频率与文献[6]中的C70E实车系统的模态试验数据进行对比。仿真模态振型频率和试验模态结果见表1,可以看出模态试验的振型频率与本文模态仿真的振型频率基本一致,验证了本文建立模型的合理性。
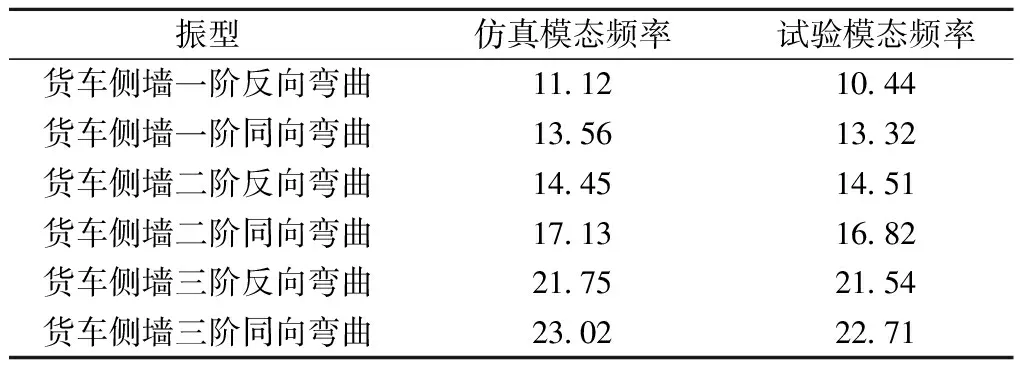
表1 模态振型频率结果对比 Hz
为了进一步验证模型的动力学性能是否与实际情况相近,在Simpack多体动力学软件中计算货车模型的非线性临界速度,并与实际的临界速度进行对比。在Simpack软件中,使货车通过有初始激励的路段,观察货车在平直无不平顺路段的轮对横移量是否收敛来计算货车的临界速度[8]。由中车齐齐哈尔车辆有限公司研制的C70E货车空车时的临界速度范围为140~150 km/h,当采用斜楔等效作用法处理斜楔时,货车第一轮对和第三轮对横移量如图8所示,在速度为139 km/h时收敛,在速度为140 km/h时处于临界状态,货车临界速度为140 km/h,与实际的临界速度接近。
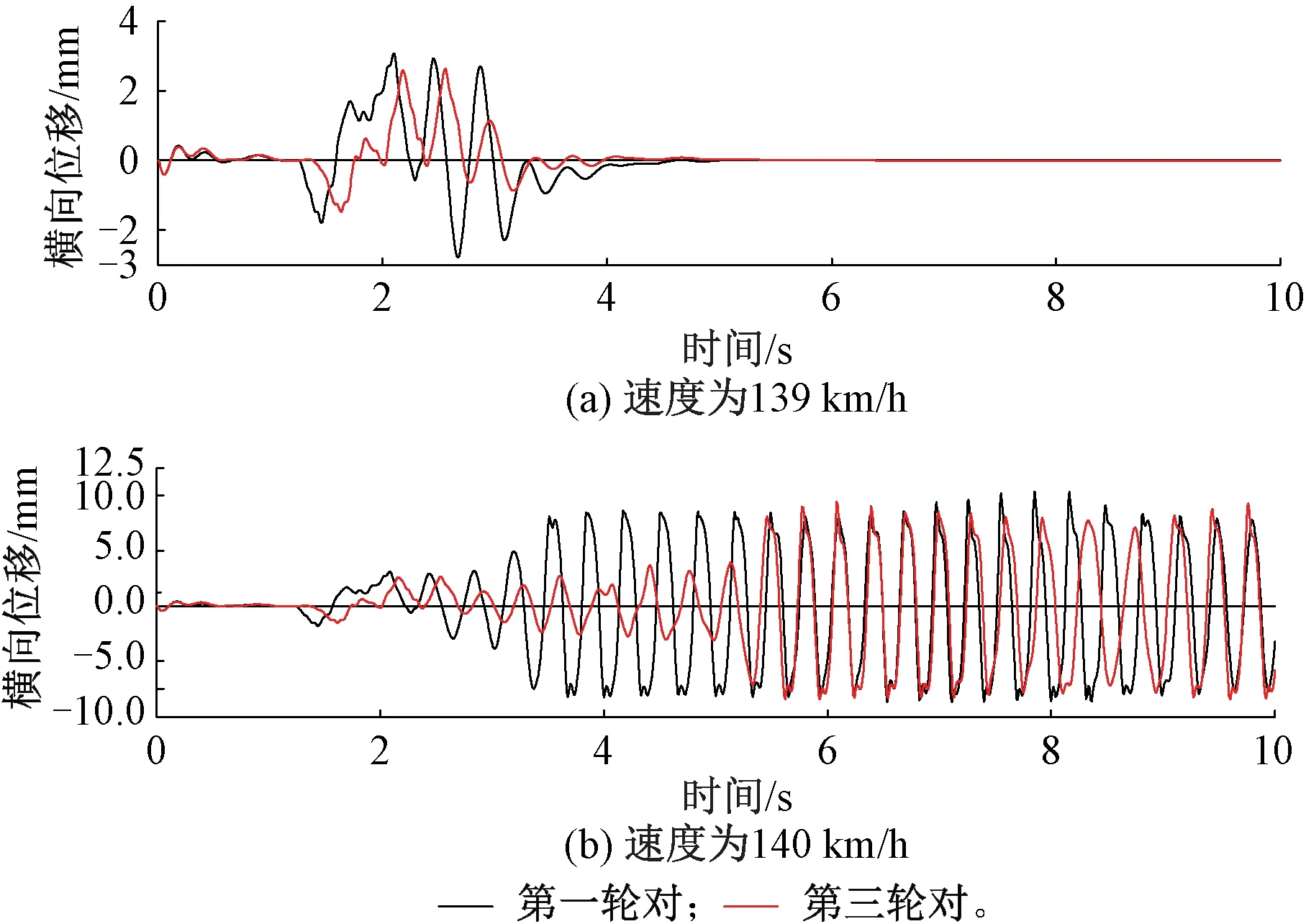
图8 斜楔等效作用法临界速度
综上,本文建立的C70E货车刚柔耦合模型的模态特征与实际货车基本一致,模型的临界速度也与实际临界速度接近,验证了货车模型的准确性。因此采用本文提出的斜楔等效作用法处理斜楔能得到一个准确的货车模型,提高了铁路货车多体动力学分析的准确性,同时该处理方法复杂程度较低,更利于计算不同斜楔参数下的货车车体响应。
3 斜楔参数优化
相对于横向,斜楔在转向架的垂向和纵向起着更大的减振作用[1]。本文选取车体垂向和纵向加速度作为优化指标,评价斜楔参数对转向架减振性能的改善。然而由于货车系统的复杂性,难以推导斜楔参数与车体响应之间的解析公式,尤其是考虑货车车体及转向架柔性时,难度将大幅增加。因此,当考虑货车部件柔性作用时,采用传统解析方法对斜楔参数进行优化是难以实现的。
考虑上述问题,本文采用数据驱动的方法建立斜楔参数与货车车体垂向和纵向加速度响应的关系模型,并以此关系模型为基础采用遗传算法对斜楔参数进行寻优,在一定合理参数范围内,找到使车体加速度响应最小的斜楔参数,具体步骤如图9所示。输入不同的斜楔角度α、主摩擦系数μ1、副摩擦系数μ2,代入斜楔各向等效作用式(2)~式(5)进行计算,根据作用公式的计算值在Simpack中设置斜楔各向等效参数力元,利用建立好的C70E货车刚柔耦合整车模型,计算货车在运行速度120 km/h下,在德国高激励轨道谱[6]上的车体垂向加速度及纵向加速度,得到不同斜楔参数下的车体加速度响应数据。根据斜楔参数响应数据,利用数据驱动的方法建立如图10所示的斜楔参数与车体加速度关系模型,并根据此关系模型对斜楔进行参数优化。以此关系模型为基础,采用遗传算法对斜楔角度、主摩擦系数、副摩擦系数进行参数编码,在一定合理参数范围内,寻求使车体垂向加速度与纵向加速度之和最小的斜楔参数组合。
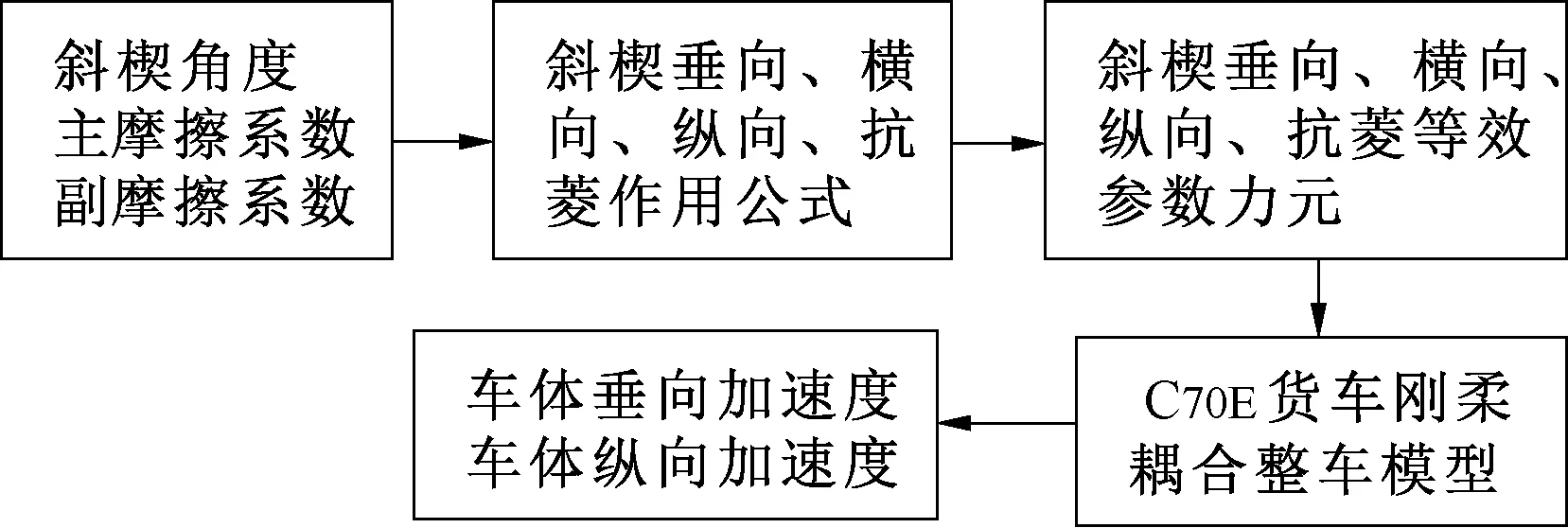
图9 斜楔参数——车体响应流程
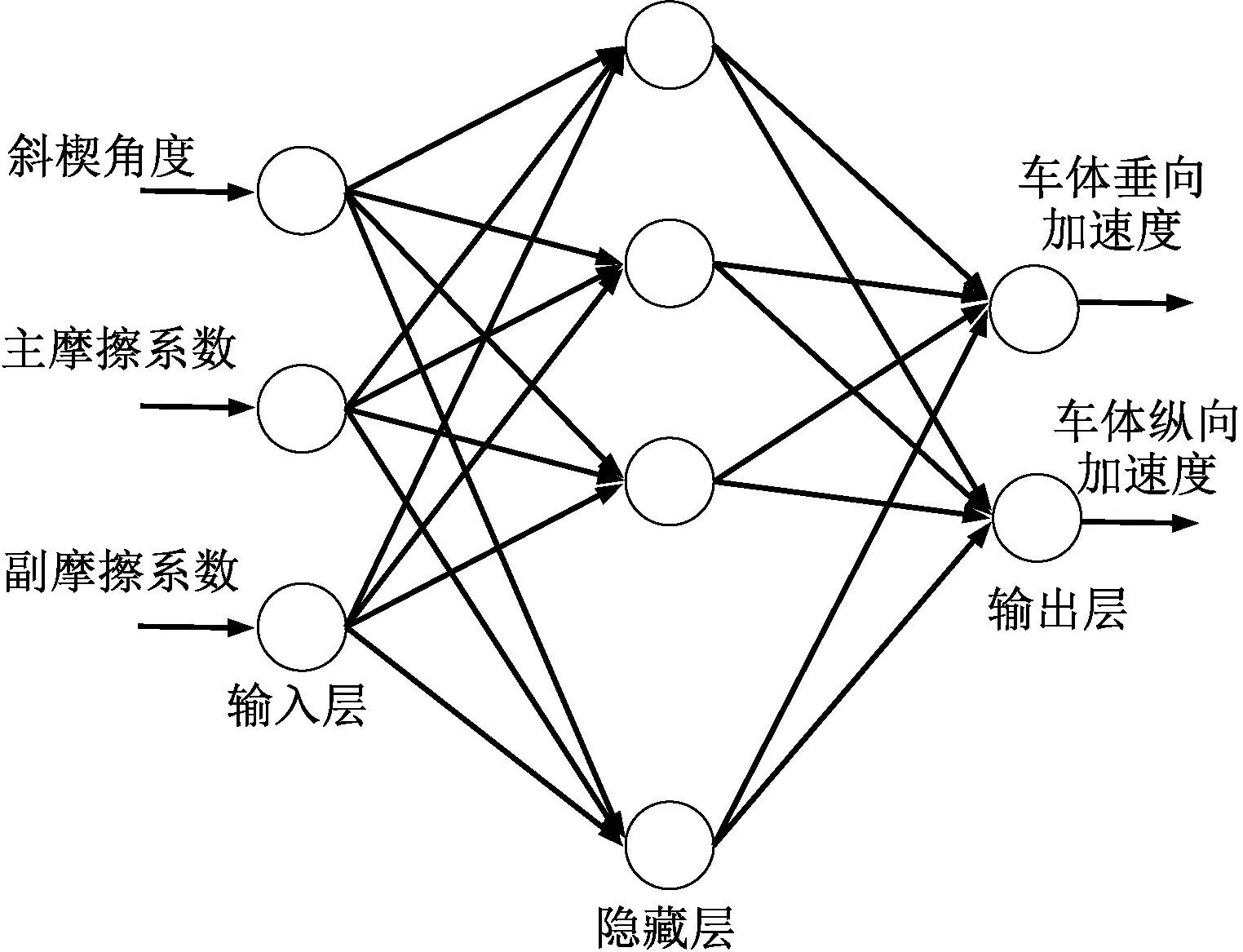
图10 斜楔参数——车体响应关系模型
3.1 BP神经网络模型
人工神经网络常用于解决模式识别中的非线性映射或分类问题,近年来在铁路车辆领域得到了大量应用,推进了铁路车辆相关研究领域的发展[15-18]。BP神经网络是人工神经网络中应用最广泛、发展比较成熟的一种,通过对训练样本进行学习,合理提取样本中的规则,对测试样本具有预测能力。但BP神经网络的全局搜索能力较差,易陷入局部极值点,影响预测精度。而遗传算法是一种基于生物自然选择和遗传机理的随机搜索和优化方法,具有较强的全局寻优能力。因此本文使用遗传算法优化的BP神经网络建立斜楔参数与车体响应的关系模型,使用遗传算法对BP神经网络的初始权值和阈值进行优化,使BP神经网络达到全局最优。
遗传算法优化BP神经网络的步骤如图11所示,遗传算法以BP神经网络的初始权值和阈值作为优化的个体参数进行编码,以BP神经网络的误差作为适应度值,对参数编码进行选择、变异和交叉操作,对参数不断进行遗传优化,得到在一定范围内使BP神经网络精度最高的初始权值和阈值,最后经过训练得到满足精度的神经网络模型。
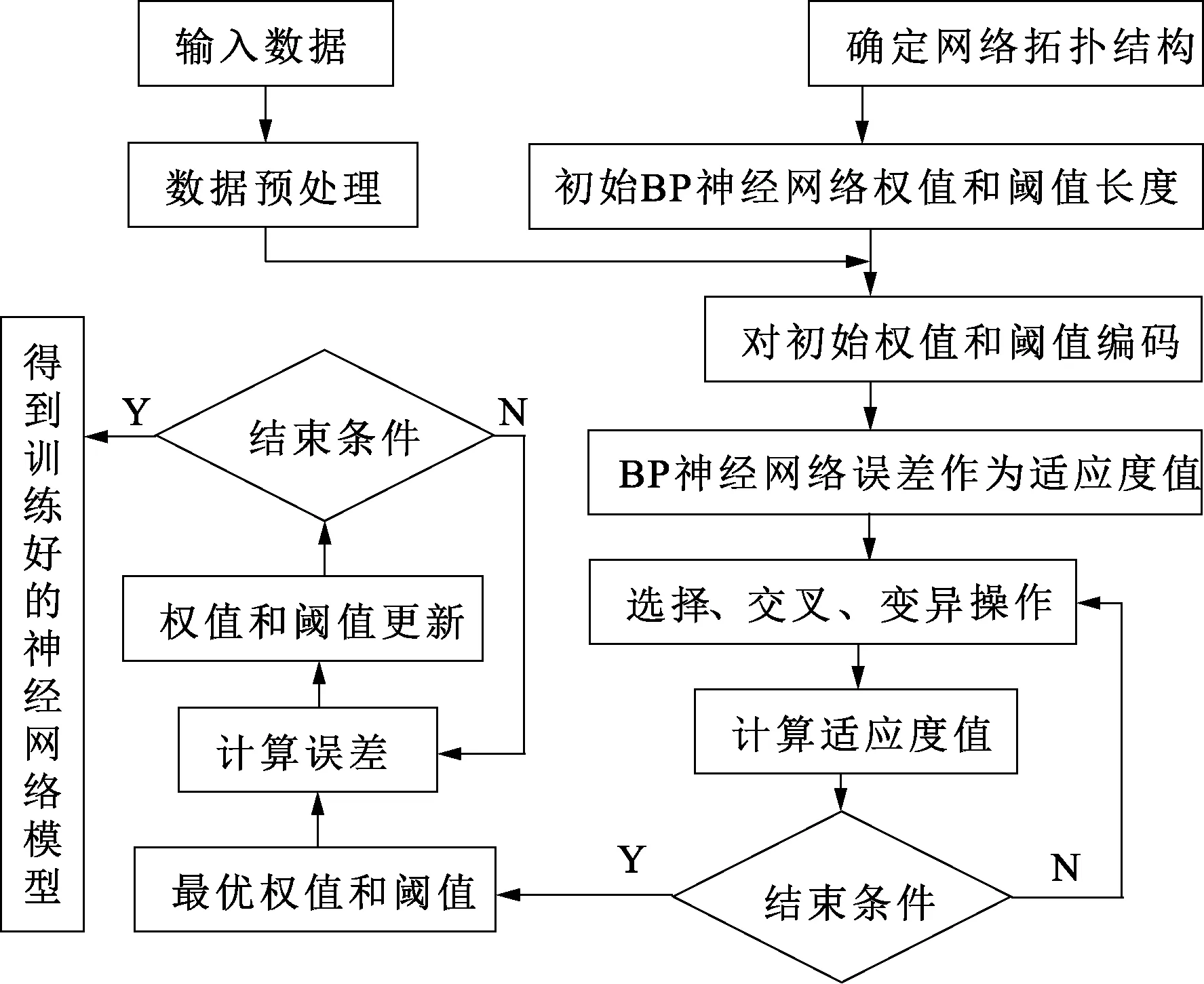
图11 遗传算法优化BP神经网络流程
为了得到斜楔参数与车体垂向以及纵向加速度的样本数据,选取8组斜楔角度、8组主摩擦系数及8组副摩擦系数,总计512组参数组合作为输入样本数据,见表2。
根据斜楔等效作用公式,当等效刚度小于0时,对摇枕施加一个方向的主动力,无法发生对应方向的位移,斜楔发生自锁,因此需保证斜楔等效作用式(2)、式(4)、式(5)均大于0才能保证斜楔不发生自锁,于是有
(6)
根据式( 6 ),将512组斜楔参数组合中发生自锁的斜楔参数组合排除,得到266组不发生自锁的斜楔参数组合,根据图11所示流程,计算266组斜楔参数下的车体垂向和纵向加速度均方根有效值(RMS),266组参数组合中的垂向、纵向以及垂向与纵向数值之和的最大、最小值见表3。

表3 车体加速度响应结果 m/s2
将斜楔角度α、主摩擦系数μ1、副摩擦系数μ2作为BP神经网络输入数据,车体垂向及纵向加速度RMS作为输出数据,对输入和输出数据进行归一化处理,并将266组样本数据随机打乱,前246组作为训练数据,后20组作为测试数据。BP神经网络选择双隐层结构,一层和二层节点均为30,训练函数选择LM算法,并采用如图11所示的利用遗传算法优化BP神经网络初始权值和阈值的方法进行训练。训练后得到的车体垂向加速度RMS预测结果如图12所示,平均相对误差为5.84%。车体纵向加速度RMS预测结果如图13所示,平均相对误差为7.58%,预测精度在可接受范围内。
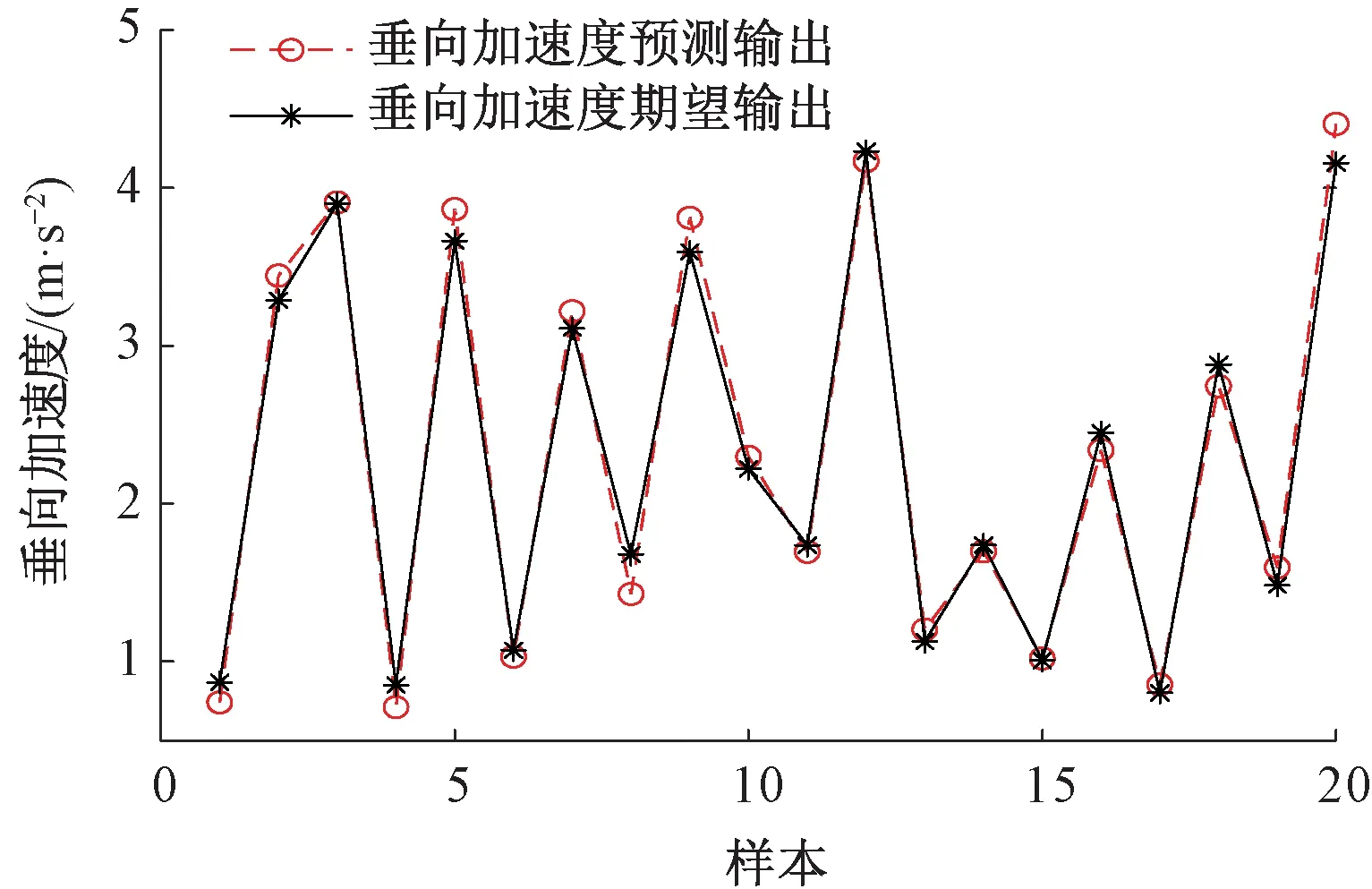
图12 BP神经网络垂向加速度预测结果

图13 BP神经网络纵向加速度预测结果
3.2 遗传算法参数优化
在得到斜楔参数与车体垂向以及纵向加速度的BP神经网络模型后,运用遗传算法对斜楔参数进行优化,对斜楔角度α、主摩擦系数μ1、副摩擦系数μ2进行编码,以训练得到的BP神经网络模型为适应度函数,将车体垂向与纵向加速度RMS之和作为适应度值。设置寻优边界:斜楔角度40°~65°,主摩擦系数0.15~0.5,副摩擦系数0.15~0.5。同时为了避免斜楔发生自锁,再设置如式( 6 )所示的边界条件。通过遗传算法中的选择、变异和交叉操作对个体进行筛选,种群反复遗传优化,直至在设置的参数边界范围内寻找到使车体垂向与纵向加速度RMS之和最小的斜楔参数。
遗传算法种群迭代适应度曲线如图14所示,在70代左右种群最佳适应度达到最优。得到最优斜楔参数:斜楔角度为49.2°、主摩擦系数为0.5、副摩擦系数为0.15。
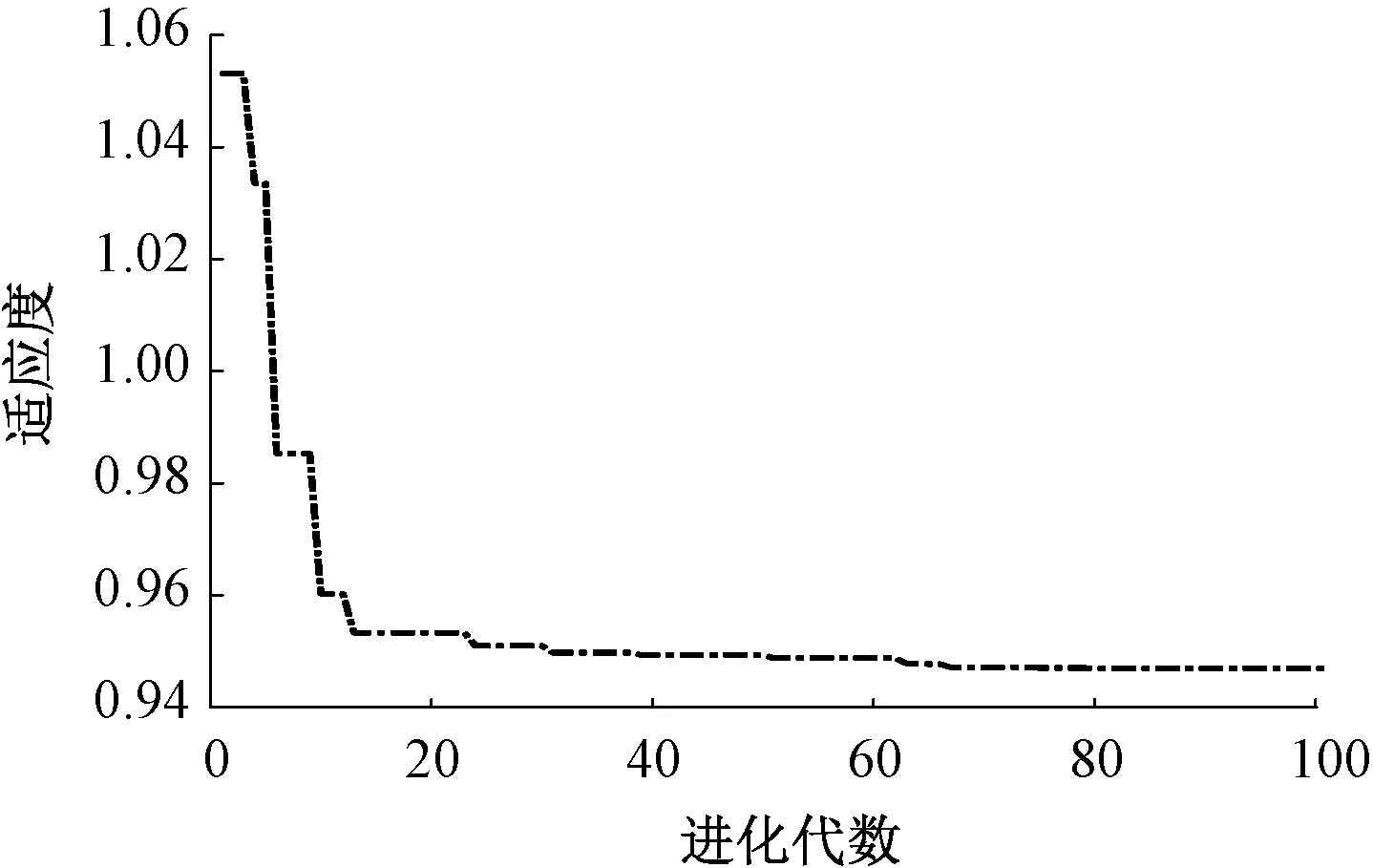
图14 遗传迭代寻优曲线
为验证优化参数是否提升了转向架的减振性能,利用建立的C70E货车刚柔耦合模型计算在最优斜楔参数下车体垂向和纵向加速度响应,并与原始斜楔参数斜楔角度58°、主摩擦系数0.24、副摩擦系数0.3下的车体加速度响应进行对比。对比结果如图15所示,原始参数下的车体垂向、纵向加速度RMS分别为1.453 8、0.384 0 m/s2;优化参数下的车体垂向、纵向加速度RMS分别为0.668 0、0.297 9 m/s2。从车身的垂向及纵向加速度对比结果可以看出,车体垂向加速度RMS下降54.1%,纵向下降22.4%,优化斜楔参数下的车体垂向及纵向加速度均有明显降低,提升了转向架的减振性能。
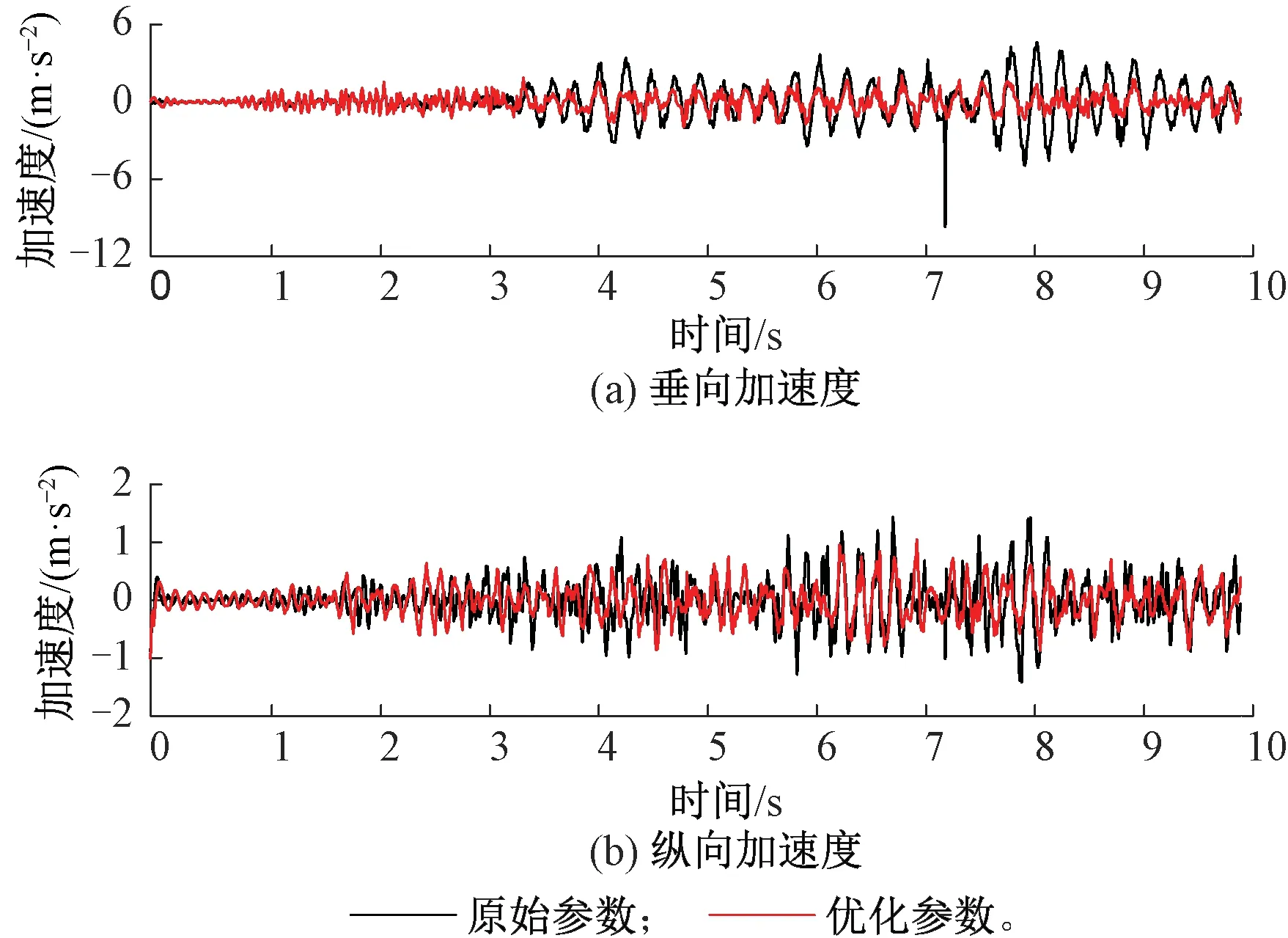
图15 车体加速度响应
同理为了验证优化参数是否提升了货车的运行稳定性和安全性,根据GB 5599—1985《铁道车辆动力学性能评定和试验鉴定规范》[19]采用脱轨系数和轮重减载率作为评定指标,利用建立的C70E货车刚柔耦合模型,对装备具有优化参数斜楔和原始参数斜楔的C70E货车的运行稳定性进行对比分析,对比结果如图16所示,货车的脱轨系数和轮重减载率均有所降低,验证了本文斜楔参数优化方法的可行性与合理性。
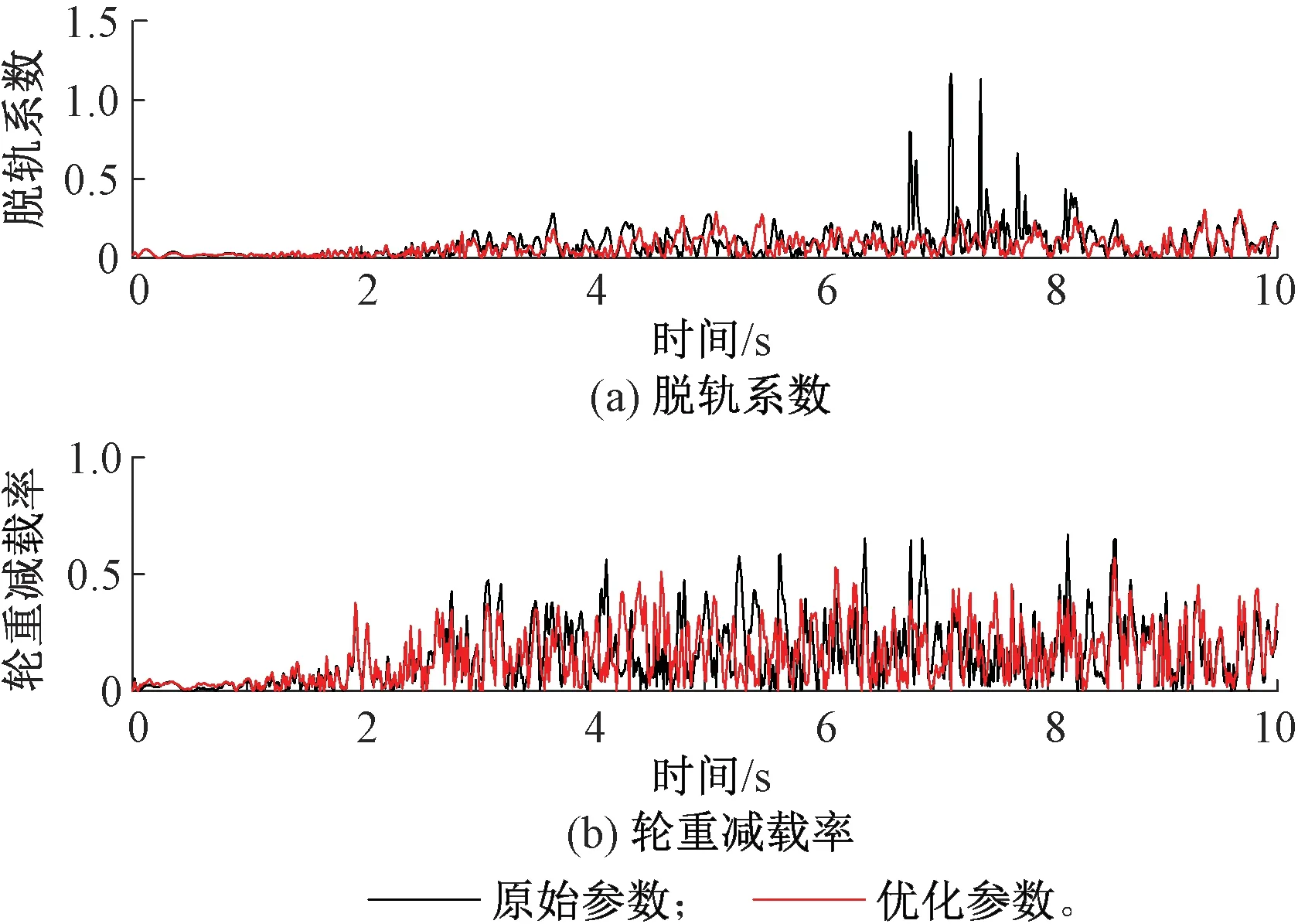
图16 货车脱轨系数和轮重减载率
4 结论
针对转向架斜楔参数优化难题,提出结合货车刚柔耦合模型、遗传算法和BP神经网络的方法实现了对斜楔参数的优化,本文的主要创新点如下:
(1)提出斜楔等效作用法处理斜楔模型,采用该方法处理斜楔的货车模型模态特征与非线性临界速度均与实际情况相近,验证了该方法处理斜楔的可行性与准确性。与建立斜楔实体模型的方法相比,计算不同斜楔参数下的车体响应更便捷,更利于使用数据驱动的方法对斜楔参数进行优化设计。
(2)提出利用货车刚柔耦合模型提取所需数据,采用BP神经网络和遗传算法建立斜楔参数与车体响应的数据驱动模型,并据此实现对斜楔参数优化的方法。利用该方法在一定合理参数选择范围内,找到使车体垂向及纵向加速度响应RMS之和最小的斜楔参数;与原始参数相比,优化参数下货车车体垂向加速度RMS下降54.1%,纵向下降22.4%,提升了转向架的减振性能;同时货车脱轨系数和轮重减载率也均有所下降,提高了货车的运行稳定性和安全性,该参数优化方法为斜楔参数设计提供了新的优化思路。

