钢筋混凝土结构锈蚀开裂模型研究

陈华鹏，刘昌雨，江 钰，肖林发

(华东交通大学 交通运输工程学院，江西 南昌 330006)

钢筋和混凝土材料良好的黏结特性使得两种不同性质的建筑材料可以有效的协同工作,同时也让结构充分发挥了材料的承载性能[1]。但是,当钢筋发生锈蚀时,混凝土结构的耐久性和承载性能就会受到严重的影响。报告显示,美国每年因锈蚀问题而产生的桥梁维修费用高达700亿美元,其中有近20%的损失是由混凝土桥的钢筋锈蚀问题造成的[2]。在英国,部分桥梁因锈蚀破坏造成的维修费用达到了造价的1.6～6倍。我国在基础设施建设过程中,钢筋混凝土结构耐久性问题也逐渐暴露,结构未达到设计年限就提前退役的现象时有发生,例如我国青海省盐湖地区的桥梁结构,使用仅2～3年就因严重腐蚀致使结构过早失效[3],其原因是钢筋表面的钝化膜被破坏,导致钢筋暴露在易腐蚀的环境中,并引起钢筋的锈蚀,而锈蚀物向外膨胀的过程会使混凝土保护层产生环向拉应力,当混凝土环向拉应力达到抗拉强度时混凝土就会开裂,产生的裂缝将进一步加速钢筋的锈蚀,使保护层剥落、结构承载性能退化,直至结构性能失效。因此,钢筋锈蚀所致混凝土的开裂问题是影响混凝土结构耐久性和承载性能的关键,揭示锈蚀引起混凝土的开裂机理对于工程结构寿命评估和维修加固等工作具有实际指导意义。

国内外学者针对混凝土开裂模型、钢筋锈胀力、混凝土性能退化等问题,开展了大量的试验、数值以及理论研究。在试验研究方面:Andrade等[4]针对钢筋位置、锈蚀速率、钢筋直径和保护层厚度等变量进行了加速锈蚀试验,建立了锈蚀深度和时间以及锈蚀速率的经验公式;Liu等[2]通过试验研究得到混凝土开裂的主要影响因素包括保护层厚度、钢筋尺寸、混凝土材料属性以及锈蚀速率等;Oh等[5]认为可以利用应变来判断开裂情况,并且建立临界锈蚀率和保护层厚度的幂函数经验公式;Rodriguez等[6]进行锈蚀加速试验,引入混凝土抗拉强度、保护层厚度与钢筋直径的比值作为变量,得到保护层表面裂缝宽度和锈蚀深度的经验公式。在数值仿真方面:Dagher等[7]建立混凝土锈蚀损伤的通用数值模型,分析混凝土的锈裂过程及性能退化;张伟平等[8]利用结构的温度膨胀特性模拟钢筋锈蚀物的膨胀作用,建立锈胀仿真计算模型,得到混凝土保护层与钢筋直径之比是影响混凝土开裂的重要因素;金伟良等[9]建立非线性有限元模型,分析均匀锈蚀和非均匀锈蚀锈胀力作用下结构的开裂过程,计算开裂时刻的锈胀力大小,并提出临界锈蚀率的计算方法。在理论研究方面:Bazant[10]提出海洋环境下锈蚀钢筋混凝土结构的数学物理模型,研究锈蚀过程中氧、氯离子的扩散和锈蚀物的组成,简化了保护层锈胀开裂的计算方法;Chen等[11]将混凝土开裂考虑为各向异性的轴对称问题,建立一种新的黏聚裂缝模型,分析裂缝的扩展全过程,预测了保护层表面的裂缝宽度变化;伦培元等[12]考虑在混凝土存在初始缺陷的情况下,提出三维半椭球形的混凝土结构锈胀开裂理论模型,认为增加混凝土保护层厚度有助于延缓结构的锈胀开裂,从而提高结构的耐久性;王海龙等[13]基于断裂力学理论建立预测开裂时刻和临界锈蚀率的混凝土锈蚀开裂模型。

以上研究较好地分析了结构锈胀开裂过程中锈胀力的变化,预测了保护层开裂的时刻和临界锈蚀率,探讨了混凝土锈蚀开裂的主要影响因素[14-16],但是对混凝土开裂全过程以及裂缝扩展的理论分析较少,无法揭示裂缝的演变机理。为此,本文基于厚壁圆筒应力理论,假设开裂混凝土的软化曲线为指数形式,提出了一种新的由钢筋锈蚀引起的混凝土保护层开裂模型。该模型将混凝土锈蚀开裂过程分为保护层未裂、部分开裂和完全开裂三个阶段,推导了每一阶段对应的应力状态、径向位移和裂缝状态等力学参数的表达式,得到了求解裂缝宽度的控制方程。此外,本文还研究了裂缝前沿的扩展规律,预测了混凝土保护层开裂的时间和锈蚀深度,揭示了裂缝的演化过程以及混凝土的刚度、强度变化规律。最后将所得结果同已有的试验数据对比分析,验证本文提出的模型。

1 锈蚀裂缝模型

Tepfers[17]最早利用弹性力学中的厚壁圆筒理论建立了模拟混凝土保护层的模型,分析开裂混凝土与钢筋的残余黏结强度,该模型也成为了研究锈蚀混凝土开裂问题的主要方法之一。本文基于混凝土材料开裂后呈各向异性的特性以及钢筋均匀锈蚀的假设,建立了三阶段厚壁圆筒开裂混凝土模型。采取钢筋均匀锈蚀假设的原因主要有:①钢筋混凝土在均匀的锈胀力作用下可以等效为受均匀内压作用的厚壁圆筒结构,将机理复杂的钢筋锈蚀导致的混凝土开裂问题考虑为轴对称问题,可以简化计算过程;②目前国内外学者为了研究混凝土锈蚀开裂问题而建立的锈裂模型大多基于均匀锈蚀的假设,且同试验数据吻合较好;③自然情况下的非均匀锈蚀分布形态受到环境、人为因素影响较大,目前仍没有一个准确的非均匀锈蚀分布预测模型,关于非均匀锈蚀导致的混凝土开裂的研究也较为缺乏,相关试验与实测数据不足。

建立的混凝土保护层锈蚀开裂模型见图1,其中,Rb为钢筋的初始半径,Ry为裂缝前端半径,C为保护层厚度,Rc为包含保护层厚度C的外部圆的半径,Ry为裂缝的前端半径,D为钢筋直径,包围着Rb的圆环代表钢筋被消耗掉一部分而产生的锈蚀氧化物。

图1 混凝土保护层锈蚀开裂模型

1.1 锈蚀过程

钢筋锈蚀主要是因为钢筋表面钝化膜被破坏,氯离子侵入混凝土内部,使得钢筋生锈,而根据锈蚀程度的不同,锈蚀物也不同,生成的锈蚀产物导致质量发生变化,单位长度的锈蚀物质量Mx为

(1)

式中:icorr(τ)为单位长度钢筋表面的年平均锈蚀电流;t为锈蚀时间;mc为经验系数取0.021[18]。

根据锈蚀物的质量,推算钢筋的体积变化ΔV为

(2)

式中:Ms为单位长度内被消耗的钢筋质量;ρx、ρs分别为锈蚀物、钢筋的密度;λm为锈蚀产物膨胀系数,研究表明,锈蚀物可能产生2～6倍的体积膨胀[20]。

锈蚀物会随着体积增大开始向外膨胀,导致钢筋表面产生径向位移ur,假设ur≪Rb且钢筋均匀锈蚀,可以表示为

(3)

式中:d为钢筋与混凝土表面间的孔隙厚度。

工程实际中均匀锈蚀的情况出现较少,更多的以点蚀或坑蚀为主。但是当锈蚀分布系数不大于2时,锈蚀产物接近均匀分布,既有研究表明,在研究裂缝扩展和结构残余寿命的问题时,采用均匀锈蚀或非均匀锈蚀两种假设造成的差异较小[19-20]。因此,均匀锈蚀的假设在本文研究中是合理的。

1.2 混凝土锈蚀开裂模型

基于钢筋均匀锈蚀的假设,模型可以简化为轴对称模型。同时混凝土在工作条件下往往产生弯曲裂纹,可以将该问题简化为平面应力问题[18]。因此,本文模型中的环向应力为主拉应力,径向应力为主压应力。当混凝土开裂后,由于混凝土的软化特性,材料的抗拉强度会随着裂缝宽度的增大而减小,根据裂缝和抗拉强度的关系引入材料的拉伸软化曲线,其主要形式有直线、双线性及指数型曲线[21-22]。直线型软化曲线由于较为理想化,与试验结果差异较大。目前大多数研究主要是基于双线性的假设,而针对指数型软化曲线的研究较少。由于指数型曲线比较符合混凝土抗拉特性,因此本文利用指数型软化曲线,建立钢筋锈蚀混凝土开裂模型。

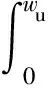
(4)

式中:σw为混凝土残余抗拉强度;kc为软化参数。W为规范化裂缝宽度,与实际裂缝宽度w的转换关系为

(5)

不同软化参数对应的指数拉伸软化曲线与典型的双线性曲线的形状对比见图2。

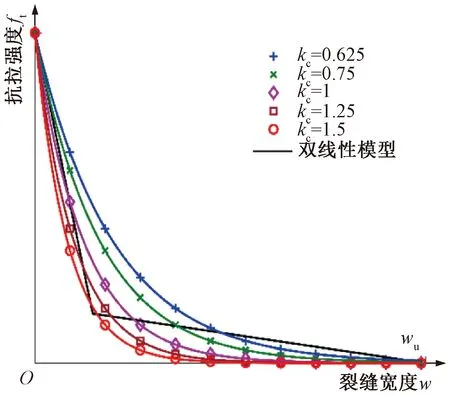
图2 不同软化参数kc的指数软化曲线与双线性软化曲线的对比

由于研究对象是结构沿纵向钢筋的截面,而且由于锈蚀深度相对钢筋的初始半径Rb非常小,因此单位锈蚀深度dr的求解可以进一步简化为单位长度锈蚀产物的体积除以其表面积求得

(6)

引入锈蚀率tr的概念,并定义其为单位锈蚀深度dr与原钢筋半径Rb的比值,即

(7)

上述的钢筋锈蚀过程忽略了结构所承受外力产生的影响。

2 裂缝扩展全过程分析

钢筋锈蚀物向外膨胀,使得混凝土产生径向位移,当混凝土的环向拉应力达到混凝土抗拉强度时,混凝土开裂,产生径向裂缝。随着时间的推移,钢筋锈蚀程度加深,裂缝逐渐加宽且向外扩展,直至混凝土保护层表面。混凝土裂缝从黏结表面扩展到保护层表面的过程中,可以分为开裂部分和未裂部分。未裂部分为各向同性问题并运用弹性理论进行分析。开裂部分的径向刚度保持不变,切向刚度受开裂影响而降低,因此可以将开裂混凝土视为正交各向异性材料,通过混凝土材料拉伸软化曲线,引入残余抗拉强度,结合断裂力学计算断裂应变及应力,考虑钢筋锈蚀产生位移边界条件,联立得到各向异性弹性体的位移协调方程,最终得到裂缝宽度的控制方程。

整个混凝土开裂过程可分为裂缝萌生、部分开裂及完全开裂三个阶段。当钢筋锈蚀物填充满混凝土孔隙区后,继续向外膨胀,当钢筋表面混凝土的环向应力达到混凝土抗拉强度时,混凝土开裂,进入部分开裂阶段。随着时间的推移,锈蚀物逐渐增加,混凝土保护层的环向拉应力越来越大,裂缝也随之向外扩展,引入裂缝前端半径Ry。当裂缝扩展到保护层表面时(Ry=Rc),结构表面开始出现裂缝,利用钢筋表面混凝土裂缝宽度Wb及其对径向坐标r的一阶导数值,求解裂缝控制方程式,从而得到保护层表面裂缝宽度变化。

2.1 裂缝萌生

此时的圆筒模型没有产生裂缝,可以采用弹性力学理论,因此各向同性弹性体的位移随径向坐标r的关系为

(8)

式中:u为径向位移;C1、C2为由边界条件确定的常系数;径向应力σr和环向应力σθ可表示为

(9)

(10)

式中:υ为混凝土材料的泊松比。

钢筋表面处的位移和混凝土保护层的径向应力边界条件为

(11)

式中:ub为黏结面位移。

将边界条件式(11)分别代入式(8)和式(9)中,解得

(12)

(13)

将解得的常系数代入式(9)中,得到径向应力σr和环向应力σθ表达式为

(14)

(15)

2.2 部分开裂阶段

此阶段,圆筒内表面已经开裂,裂缝前端向外延伸扩展,但是还未扩展至保护层表面,可以将开裂模型分为开裂部分的内筒(Rb≤r≤Ry)和弹性部分的外筒(Ry≤r≤Rc)。

外筒部分的边界条件为

(16)

式中:ft为混凝土初始抗拉强度。

利用边界条件式(16)和式(14)、式(15),径向应力σr和环向应力σθ分别为

(17)

(18)

裂缝前端的表达式可以通过裂缝前端处未裂区与开裂区的变形协调关系得到,已知弹性区与开裂区在裂缝尖端处(r=Ry)的径向位移分别为

(19)

(20)

式中:E为混凝土弹性模量。

将式(12)、式(13)代入式(19)整理得

(21)

(22)

2.3 完全开裂阶段

将开裂后的混凝土视为正交各向异性材料,为了方便求解,引入黏聚裂缝的概念,将实际的径向裂缝等效为对称分布在模型内的nc条裂缝[15],构成一个轴对称问题。基于Bazant等[23]提出的断裂带理论,混凝土保护层表面的裂缝总数nc为

(23)

式中:Lc为最小允许裂缝带宽度Lc=3da,da为混凝土的最大骨料尺寸。

(24)

(25)

式中:l0=nclch/2π,lch为Hillerborg等[24]定义的特征长度,其计算式为

(26)

因此,环向总应变εθ为

(27)

根据几何方程可得径向位移ur和径向应变εr分别为

(28)

将式(24)、式(25)、式(26)和式(27)代入式(28)得径向应变εr和径向位移ur分别为

(29)

(30)

开裂混凝土的环向刚度会随着裂缝宽度的增加而逐渐减小,引入刚度折减系数β为

(31)

根据Pantazopoulou等[18]提出的正交各向异性弹性柱体的位移协调方程,即

(32)

将式(29)和式(31)代入式(32),得到裂缝宽度关于半径r的控制方程为

(33)

式(33)是一个非线性二阶微分方程,难以直接求得规范化裂缝宽度W的显式公式。本文利用数值方法求解该微分方程,首先将方程降阶,取得某一点的W值及其一阶导数值,运用这两个初始边界条件,可以得到方程的数值解,再通过式(5)的转换就可以得到实际裂缝的宽度。

在裂缝前端到达保护层表面时,模型进入完全开裂阶段,结构表面开始出现裂缝。此时保护层表面的裂缝宽度可利用钢筋表面处的裂缝宽度Wb及其一阶导数值dW/dr两个初始边界条件求解式(33)得到。联立式(11)和式(29),得到钢筋表面裂缝宽度为

(34)

式中:函数lambertw(0,x)为f=xex的反函数,常应用于求解带有指数项的微分方程。

开裂后混凝土可以看作正交各向异性材料,其应力应变关系可表示为

(35)

(36)

考虑开裂部分环向拉应力等于其残余抗拉强度,因此将式(27)、式(30)和式(31)代入式(36),再联立式(4)和式(36),解得W对于径向坐标r的一阶导数为

(37)

利用式(34)、式(37)作为二阶微分方程的两个初始条件求解裂缝宽度控制方程式(33),得到裂缝宽度W与径向坐标r的关系,再令r=Rc得到混凝土保护层表面的裂缝宽度。

3 数值算例

3.1 模型验证

为验证本文理论模型的准确性,采用Liu等[2]得到的加速锈蚀试验数据进行对比验证。根据文献[2]中试验提供的材料参数,混凝土抗压强度fc=31.5 MPa,抗拉强度ft=3.3 MPa,弹性模量E=27 GPa,泊松比υ=0.18,混凝土蠕变系数为2,钢筋密度ρs=7 850 kg/m3,钢筋锈蚀物密度ρx=3 600 kg/m3,取λm=1.85×10-4。假设最大骨料尺寸da=25 mm,软化参数kc=1,断裂能Gf=83 N/m,裂缝总条数nc=4,极限裂缝宽度wu=0.2 mm,体积膨胀系数λm取1.85×10-4和2.17×10-4[2],分别表示取值的不确定性与可能的取值范围,用以研究体积膨胀对裂缝扩展的影响。

利用本文方法计算保护层完全开裂时间并与试验结果相比较,见表1。由表1可知,保护层完全开裂的时间会随着保护层厚度的增大而明显增加,试验结果被包含在预测的时间区间之内或非常接近预测区间,表明预测结果与试验结果吻合较好,从而验证了本文模型的准确性和有效性。

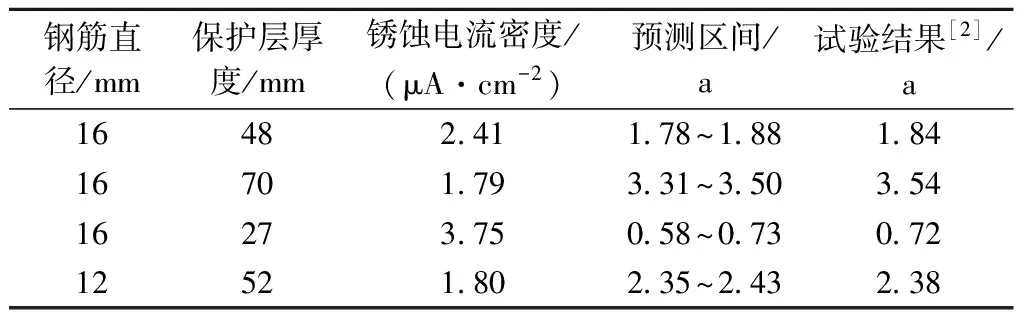
表1 不同体积膨胀系数下保护层开裂时间

3.2 参数分析

不同膨胀系数下钢筋表面处的径向位移ur随时间的变化关系见图3。由图3可知,相同时间下锈蚀膨胀系数越大,径向位移也越大。在锈蚀初期,径向位移增加的速率较快,随着时间的推移曲线趋于平缓。锈蚀时间低于5 a时,不同膨胀系数对径向位移的影响不明显,超过该年限后,径向位移的差异显著增大。并且分别在38.1、40.9、42.6 a处达到127.32 μm,对应混凝土表面裂缝宽度达到极限值wu。

图3 径向位移ur随时间变化

不同体积膨胀系数下钢筋表面处的裂缝宽度随时间的变化见图4,由图4可知,钢筋表面处的裂缝宽度随时间的变化同径向位移相似,同样也是在38.1、40.9、42.6 a时达到裂缝极限值wu。

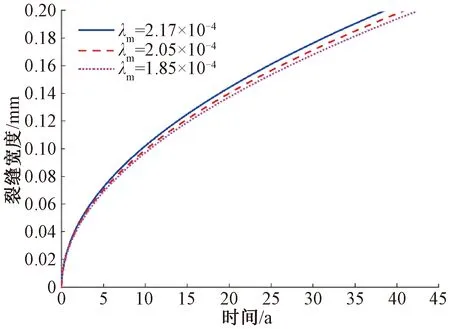
图4 不同体积膨胀系数下钢筋表面处裂缝宽度随时间变化

为了解钢筋表面和保护层表面的裂缝宽度的时间特征差异,绘制了λm=1.85×10-4时两者随时间的变化曲线见图5。由图5可知,保护层表面在初期并没有出现裂缝,当锈蚀时间达到1.88 a时,表面突然出现裂缝,且宽度瞬间升至0.04 mm,这是由于混凝土在开裂时存在应力瞬间释放现象。钢筋表面的裂缝则随时间的增长持续增大,且由于锈蚀物向外膨胀,其裂缝宽度要略大于保护层裂缝宽度。随着时间的推移,两者的差值会逐渐减小并趋于相同,最终在42.6 a时达到极限裂缝宽度值0.2 mm。这主要是由于锈蚀时间达到一定时,锈蚀产物逐渐增多,锈胀力会持续增大,使得钢筋表面的裂缝逐渐向保护层裂缝贯通。

当λm=1.85×10-4时,裂缝前端从钢筋表面扩展到保护层表面的全过程见图6。由图6可知,裂缝前端在1.88 a左右的时间点到达了保护层表面。裂缝前端在接近钢筋表面和保护层表面时,其扩展速率明显快于中间部分,同样是由于在开裂初始阶段和最终阶段应力释放现象导致的。

钢筋表面和保护层表面的环向应力随时间的变化曲线见图7。钢筋表面由于开裂较早,所以在经历了短暂的初裂过程之后环向应力由混凝土抗拉强度值开始呈指数下降,直至接近为0。保护层表面处环向应力由于受到膨胀作用,在1.88 a的时间内升高至3.3 MPa,达到混凝土的抗拉强度,随后保护层表面开裂,并同样以指数形式急剧降低并逐渐趋于0。

为研究临界钢筋锈蚀深度(混凝土保护层开裂时锈蚀深度)同保护层厚度与钢筋直径之比(C/D)的关系,根据文献[25]提供的试验参数计算得到理论预测结果,见图8。同相应试验结果相比,可以发现,本文模型的预测结果与试验值吻合较好,临界锈蚀深度与保护层和钢筋直径之比C/D的关系呈正线性相关规律。

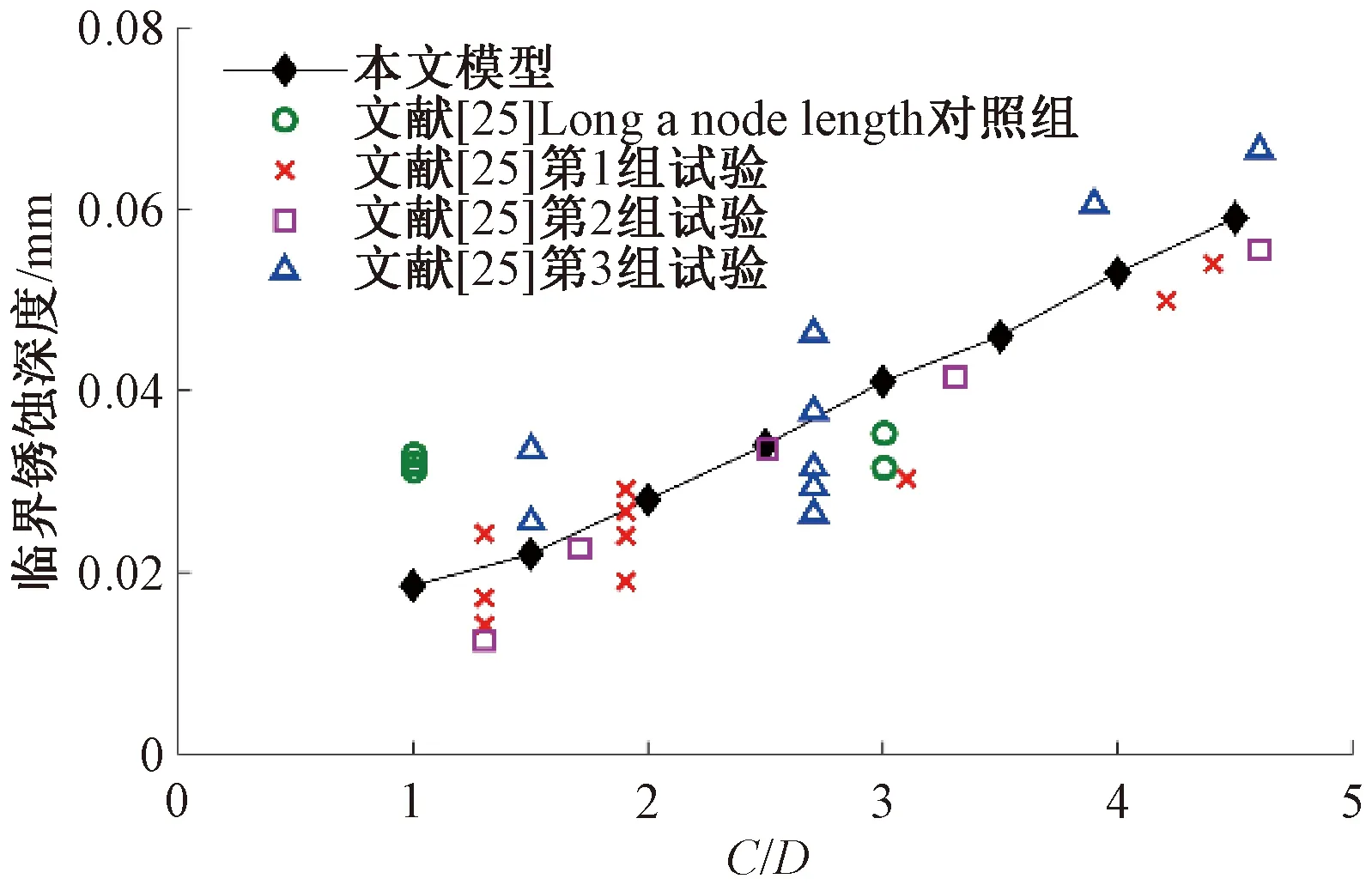
图8 不同保护层厚度与钢筋直径之比的临界锈蚀深度

等效裂缝宽度随锈蚀率的变化曲线见图9。锈蚀水平较低时,无裂缝产生。当锈蚀率达到某一临界值时(约为0.004 1),保护层表面完全开裂。裂缝达到0.04 mm后,随着锈蚀率的增加裂缝宽度近似呈线性增长。进一步地,将本文的预测结果与大量试验结果[26-30]进行对比,可以发现本文的模型预测结果与大部分试验结果吻合程度较好,也进一步地验证了本文所提出方法的准确性。

混凝土表面裂缝宽度在不同锈蚀电流的情况下随时间的变化关系见图10。由图10可知,锈蚀电流的增大会导致裂缝提前出现。随着锈蚀电流从0.3 μA/cm2增加至5 μA/cm2,在相同的锈蚀时间下,裂缝宽度将会明显变大。此外,锈蚀电流越大,裂缝的增长速率也显著增大,尤其是锈蚀电流超过1 μA/cm2以后。由此可见,锈蚀电流对混凝土开裂与裂缝扩展有着显著的影响。

钢筋表面和保护层表面处刚度折减系数β随时间的变化见图11。未开裂时,刚度折减系数被假定为1。由图11可知,在钢筋表面,刚度折减系数β伴随着混凝土开裂急剧下降,在1.88 a时即保护层表面开裂的时刻就已经降到了0.01以下,而保护层表面的刚度从开裂后骤降至0.08左右,随后继续快速下降。因此,混凝土保护层在开裂过程中其刚度下降的速度要快于强度衰减的速度。

在不同的锈蚀物膨胀系数下,混凝土结构的临界锈蚀深度随混凝土抗拉强度的变化见图12。结果表明,锈蚀产物膨胀系数从1.85×10-4增大到2.17×10-4过程中,临界锈蚀深度有了明显的减小。因此,锈蚀产物的膨胀系数越大,结构的锈蚀破坏发生得越快。随着混凝土抗拉强度的增大,混凝土结构的临界锈蚀深度逐渐增大,但是随着锈蚀产物膨胀系数的增大,抗拉强度对临界锈蚀深度的影响会有所削弱,其曲线也相对比较平缓。

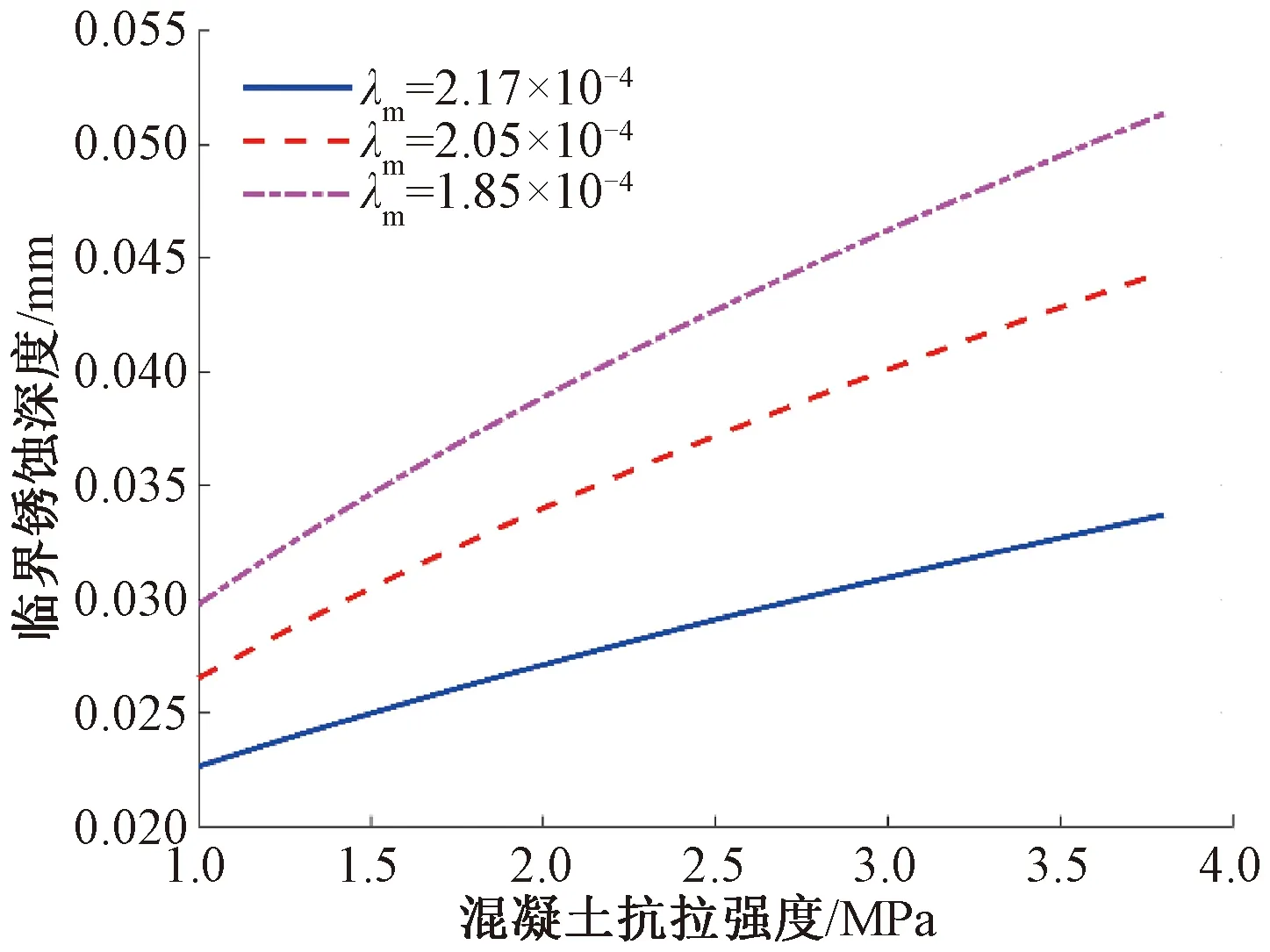
图12 不同膨胀系数下临界锈蚀深度随混凝土抗拉强度的变化

4 结论

本文考虑混凝土开裂后的抗拉强度指数型软化形式,提出了基于时间及锈蚀率的混凝土锈蚀开裂模型,研究了混凝土锈胀开裂全过程,主要结论如下:

(1)推导了裂缝宽度沿着径向坐标r的控制方程并给出了数值求解方法,预测了混凝土保护层表面完全开裂的时间,并利用试验数据进行对比,验证了模型的有效性。

(2)研究了裂缝扩展全过程,推导了裂缝前端及各阶段相关力学参数的公式,利用数值算例研究了径向位移和裂缝宽度随时间的变化规律。

(3)在锈蚀初期,混凝土表面的环向应力会迅速上升,当裂缝到达保护层表面时,混凝土抗拉强度急剧下降,而切向刚度则将会以更快的速度衰减。

(4)混凝土保护层厚度与钢筋直径之比(C/D)、混凝土抗拉强度和锈蚀膨胀系数等因素直接影响着保护层锈蚀开裂时间。锈蚀电流直接与锈蚀速率相关,工程应用中可以通过测定、控制锈蚀电流来解决相应的混凝土结构耐久性问题。

(5)通过引入锈蚀率的概念来描述钢筋锈蚀程度,发现锈蚀率和裂缝宽度之间呈正线性相关,并通过大量试验数据对比分析,发现试验结果与预测结果吻合程度较好,进一步验证了本文模型的有效性和准确性。

(6)利用保护层外表面的裂缝宽度,结合结构允许的最大裂缝宽度以及钢筋锈蚀率,可以预测结构剩余寿命;同时,结合时变结构失效风险分析与全寿命成本分析,可以指导混凝土结构的维修加固以及优化维护方案。