基于冲击弹性波波速的铁路混凝土疲劳损伤评价方法

李化建，赵国堂，高 亮，温家馨

(1.北京交通大学 土木建筑工程学院，北京 100044；2.中国国家铁路集团有限公司，北京 100084；3.中国铁道科学研究院集团有限公司 高速铁路轨道系统全国重点实验室，北京 100081)

高速铁路、重载铁路、城际铁路等铁路混凝土结构服役期间除受抗压、抗弯等静载外,还要承受列车疲劳荷载作用。在疲劳荷载及环境侵蚀因素的耦合作用下,混凝土内部损伤累积易导致铁路结构出现疲劳开裂破坏,影响结构的耐久性和列车运行安全性[1-4]。从损伤累积的角度来看,混凝土的疲劳损伤过程是在循环荷载作用下裂缝产生、扩展、恢复的过程,骨料和砂浆间的粘结裂缝和砂浆内部的微裂缝贯穿,继而形成连续的宏观缺陷,最终导致结构的服役性能下降[5]。

裂缝与混凝土结构的服役性能直接相关且易于观测,可根据裂缝恢复与扩展的形式判断疲劳荷载下损伤的累积过程,因此,以裂缝为混凝土结构疲劳性能损伤的评价依据是目前的常用方法[6-8]。同时,变形[9-10]和残余强度[3,11]等宏观性能也被用于疲劳性能的评价。但由于混凝土组成多样、疲劳荷载作用复杂等原因,根据宏观性能评价的方法无法观测疲劳损伤在混凝土内积累的现象,且存在人为因素影响大、可重复性差、结果离散性大等缺点。无损检测可解决宏观性能作为疲劳性能评价参数所存在的问题,常用无损检测参数包括超声波、声发射及电信号等。朱劲松等[12]通过对100 mm×100 mm×100 mm混凝土试块进行疲劳加载并测量其超声波速的变化,得出疲劳加载后混凝土的损伤情况。Noorsuhada等[13]使用声发射技术对混凝土梁拉伸裂缝和剪切裂缝进行检测,发现裂缝随着荷载的增加成比例扩展。Suchorzewsk等[14]将铜片插入混凝土以测量其电阻率,并以电阻率的相对值对混凝土内部状态进行评价,结果表明动载作用下混凝土的相对电阻率呈现周期变化,相对电阻率随内部缺陷发展呈现逐渐增大的趋势,且在即将破坏前激增。除上述方法外,冲击弹性波在混凝土损伤检测中的应用也越来越受到重视[15]。冲击弹性波具有频率低(2～4 Hz)、波长长(1～2 m)和穿透性强的特点,且冲击弹性波波速在混凝土内部缺陷处发生变化,通过分析其变化规律即可确定结构的完整性及缺陷的位置[16]。相关研究证明,冲击弹性波在混凝土力学性能与缺陷检测中具有较好的精度[17-18]。孙其臣等[19]使用冲击弹性波波速计算混凝土动弹模量,并通过波速损失反映因冻融循环造成的混凝土动弹模损失。李化建等[20]提出了基于冲击弹性波波速的混凝土动态损伤变量的测试方法,为混凝土动态性能细观损伤定量评价提供了新思路。

目前冲击弹性波检测多应用于水工、民建等强度等级较低的混凝土中,以检测其力学性能及内部缺陷,尚缺少在铁路高强度等级混凝土疲劳性能方面的研究。基于此,本文提出以冲击弹性波作为评价参数的疲劳性能评价方法,定义了基于弹性波波速的损伤变量;对比静态加载和抗折疲劳下损伤变量的变化规律,验证该方法的可行性;研究疲劳荷载下不同强度等级、不同饱水状态混凝土冲击弹性波波速的变化规律,证明该方法的适用性;结合铁路混凝土疲劳损伤特征,确定铁路混凝土疲劳损伤临界状态判定指标。

1 试验

1.1 原材料

水泥:北京金隅集团有限公司生产的P·O 42.5普通硅酸盐水泥,其化学组成及主要性能见表1和表2。

表1 水泥化学组成(质量分数) %

表2 水泥主要性能

粉煤灰:元宝山电厂F类Ⅰ级粉煤灰,密度为2.25 g/cm3,主要参数见表3。

表3 粉煤灰主要参数 %

矿渣粉:河北唐山唐龙新型建材有限公司生产的S95级矿渣粉,密度为2.81 g/cm3。

骨料:细骨料为细度模数2.8、级配Ⅱ区的天然河砂;粗骨料为5～10 mm、10～20 mm连续级配石灰岩碎石。

减水剂:聚羧酸系高性能减水剂,减水率27%,固含量40%。

拌和水:自来水,符合混凝土拌和用水的规定。

1.2 配合比

设计水胶比为0.40、0.27和0.23的三组混凝土,配合比见表4,编号分别为C1、C2、C3。控制新拌混凝土坍落度为(160±20) mm,含气量为(3±1)%。搅拌成型后置于温度(20±5) ℃的室内养护24 h,拆模后将混凝土试件置于标准养护条件下养护至规定龄期。

表4 混凝土配合比 kg/m3

1.3 试验方法

力学性能试验:按照GB/T 50081—2019《混凝土物理力学性能试验方法标准》[21]测试混凝土抗压强度、抗折强度和轴心抗压强度,每组3个试件。试验测得C1、C2、C3混凝土28 d龄期抗压强度分别为48.4、65.4、80.1 MPa,抗折强度分别为5.5、6.4、7.8 MPa,轴心抗压强度分别为45.8、63.7、78.7 MPa。

静载试验:参照GB/T 50081—2019《混凝土物理力学性能试验方法标准》[21],对100 mm×100 mm×100 mm抗压强度试件和100 mm×100 mm×400 mm抗折强度试件分别加载至荷载率为0.2、0.4、0.6、0.8和1.0后卸载,测试其冲击弹性波波速。定义荷载率R为

R=f/fc

(1)

式中:f为实际荷载,MPa;fc为峰值荷载,MPa。

疲劳试验:采用SUNS-890电液伺服动静万能试验机进行抗折疲劳试验。每组试验需3个试件,试件尺寸为100 mm×100 mm×400 mm,应力水平为0.6,应力下限为1 kN,加载频率为5、10、15、20 Hz,读取加载端位移数据。

冲击弹性波试验:按照JGJ/T 411—2017《冲击回波法检测混凝土缺陷技术规程》[22]中冲击回波法的检测要求,使用混凝土多功能无损测试仪测量试件的冲击弹性波(P波)波速,测试原理见图1(a)。测试选用直径为17 mm不锈钢球做激振锤;受信点位于端面中心,沿端面对角线布置4个激振点,每个激振点至少激振5次以保证能够拾取有效数据,见图1(b)和图1(c)。

图1 冲击弹性波波速测试原理及方法

断面图像分析:根据混凝土断面中骨料断裂、浆体断裂和砂浆-骨料界面断裂三种主要破坏形式的差异,采用Image Pro Plus软件将断面图像转换为8位灰度图像,然后进行图像计算分析。其中,砂浆-骨料界面断裂后两侧形貌明显不同,且在光学显微镜下,界面光滑且颜色均匀,可根据此特点进行识别。此外,砂浆-骨料界面断裂的比例可根据界面断裂面积/总面积进行计算。

2 结果与分析

2.1 基于冲击弹性波波速的损伤变量

冲击弹性波在穿过混凝土内部缺陷表面时会产生反射和透射,导致波速衰减,决定其反射量和透射量的因素是物体与媒质分界面两侧物质的声阻抗率的大小。混凝土内反射波和透射波速度的计算式为

(2)

(3)

式中:vin、vre和vtr分别为入射波、反射波和透射波质点振动速度;Zs、Zsi分别为入射介质和反射介质的阻抗率,kg/m2·s;n为介面数。当混凝土内部存在缺陷时,其内部以空气和水充填,混凝土、水和空气的阻抗率分别为7～10、0.5、0.4 kg/m2·s[18]。

结合式(2)和式(3)可知,当混凝土内部存在缺陷时,其冲击波波速会产生衰减,且缺陷数量越多衰减越明显,但混凝土缺陷情况与波速不存在简单的对应关系。由冲击弹性波波速所定义的损伤变量应基于以下原则:

(1)具有明确的数学和物理意义。

(2)为量化评价疲劳损伤情况,以损伤参数的相对值来定义损伤变量,避免绝对值的离散性。

(3)结果易于测量且有明显变化。

动弹性模量与混凝土自身的结构性能密切相关,能反映出局部破损与刚度损失,且混凝土动弹性模量Ed与冲击弹性波波速v有直接关系,即

(4)

式中:ρ、μ分别为密度、泊松比。

泊松比和密度在混凝土损伤过程中变化较小,根据线性损伤累积理论,通过相对动弹模量定义的损伤变量D为

(5)

式中:Ed0为疲劳试验前动弹性模量,GPa;EdT为疲劳试验后动弹性模量,GPa;vd0为疲劳试验前冲击弹性波波速,m/s;vdT为疲劳试验后冲击弹性波波速,m/s。

选择冲击弹性波波速为评价参数可与动弹模量建立联系,损伤变量能够综合反映混凝土经过疲劳荷载后的损伤程度。

2.2 混凝土中冲击弹性波波速变化规律

2.2.1 静态加载试验结果

图2为静态加载不同荷载率时混凝土冲击弹性波波速和损伤变量变化规律。

图2 不同荷载率混凝土冲击弹性波波速与损伤变量

由图2可知,混凝土冲击弹性波波速随应力的增大而降低,损伤变量随应力的增大而上升,损伤变量随着荷载率的增加呈现出线性增加趋势。受压状态下C1混凝土在加载后平均冲击弹性波波速由4 482 m/s降低到4 146 m/s,下降幅度为7.5%;C2混凝土平均冲击弹性波波速由4 638 m/s降低到4 284 m/s,下降幅度为7.6%;C3混凝土平均冲击弹性波波速由4 795 m/s降低到4 365 m/s,下降幅度为8.9%。破坏前C1、C2和C3混凝土的损伤变量分别上升到了0.147、0.142和0.171。抗折状态下波速呈现先慢后快的发展趋势,其中,C1混凝土在加载后平均冲击弹性波波速由4 450 m/s降低到3 863 m/s,下降幅度为13.2%;C2混凝土在加载后平均冲击弹性波波速由4 644 m/s降低到4 015 m/s,下降幅度为13.5%;C3混凝土在加载后平均冲击弹性波波速由4 758 m/s降低到4 134 m/s,下降幅度为13.1%。破坏前C1、C2和C3混凝土损伤变量分别达到0.244、0.253和0.247。

从静态加载结果上看,不论是抗压还是抗折,混凝土在荷载作用下损伤增加,体现为冲击弹性波波速发生衰减,损伤变量增加。比较而言,抗压荷载作用下混凝土的冲击弹性波波速与损伤变量变化小于抗折荷载作用,其原因是抗压荷载作用下的混凝土的裂纹从承压面外沿向内部以一定角度扩展直至试件失效,但这时被羁留在内侧的混凝土在压应力的作用下的损伤不明显,而在抗折荷载作用下下混凝土在弯矩和剪应力的作用下裂纹沿薄弱面逐渐贯通试件,呈现整体开裂破坏,相比于抗压破坏的损伤程度更高。

2.2.2 疲劳加载试验结果

试验选择强度与轨道板混凝土强度接近的C2混凝土为试验对象,其抗压强度为65.4 MPa,抗折强度为6.4 MPa。图3为疲劳加载下冲击弹性波波速与损伤变量变化规律。

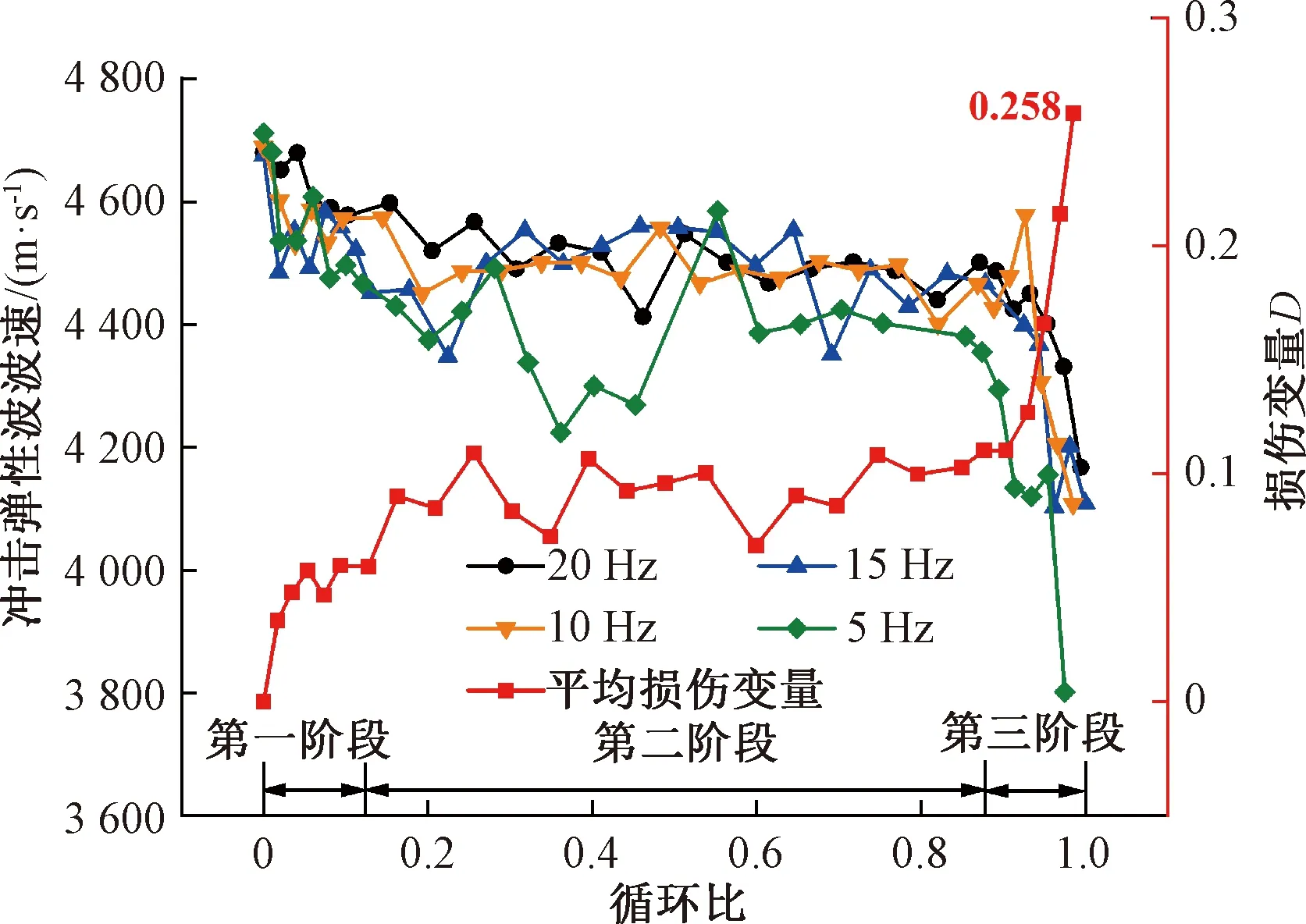
图3 疲劳加载下冲击弹性波波速与损伤变量

由图3可知,混凝土冲击弹性波波速随疲劳荷载循环比(N/Nf)增加而降低,不同加载频率下的冲击弹性波波速与损伤变量均呈现出明显的三段式发展规律,与相关研究结果相同[12-14]。第一阶段处于0～0.15倍疲劳寿命的范围内,此时呈现出波速快速减小、损伤变量增长快的特点;第二阶段处于0.15～0.9倍疲劳寿命的范围内波速和损伤变量变化很小,均处于稳定状态;第三阶段处于0.9～1.0倍疲劳寿命的范围内,波速急剧降低,损伤变量快速增大,呈现突变特征。疲劳加载前、稳定发展阶段初期、稳定发展阶段末期、疲劳断裂前弹性波波速分别为4 675、4 573、4 426、4 046 m/s,相应的损伤变量随疲劳加载逐渐增加,疲劳破坏前损伤变量达到0.258。在不同加载频率5、10、15、20 Hz作用下,混凝土冲击弹性波波速的变化规律相似,均呈现出三阶段的变化特征,且三阶段所占疲劳寿命比例相当,表明在5～20 Hz范围内,加载频率对混凝土疲劳发展的三阶段特征及比例影响较小。

图4为静态加载与疲劳加载下混凝土抗折应力-应变曲线。由图4可知,静态加载时应力随应变增大而增大,在到达峰值应力后快速下降,混凝土破坏时应变为451×10-6。在疲劳加载中,第一次加载时混凝土应力-应变加载曲线与静态加载曲线基本重合,混凝土应变随疲劳次数的增加而逐渐增加,应变达到479×10-6时发生破坏。混凝土疲劳作用下最大应变大于静态抗折破坏时的最大应变,这是因为疲劳荷载使混凝土的弹性模量下降,混凝土的刚性降低导致变形增大。结合图2(b)可知,破坏前静态抗折状态下的损伤变量与疲劳荷载下的损伤变量相差不大,分别为0.253和0.258,但发展趋势有明显区别。这是因为静态加载中混凝土内损伤随应力增大而单调增大,而疲劳荷载中应力大小保持恒定,混凝土内部损伤随疲劳加载而逐步累积。

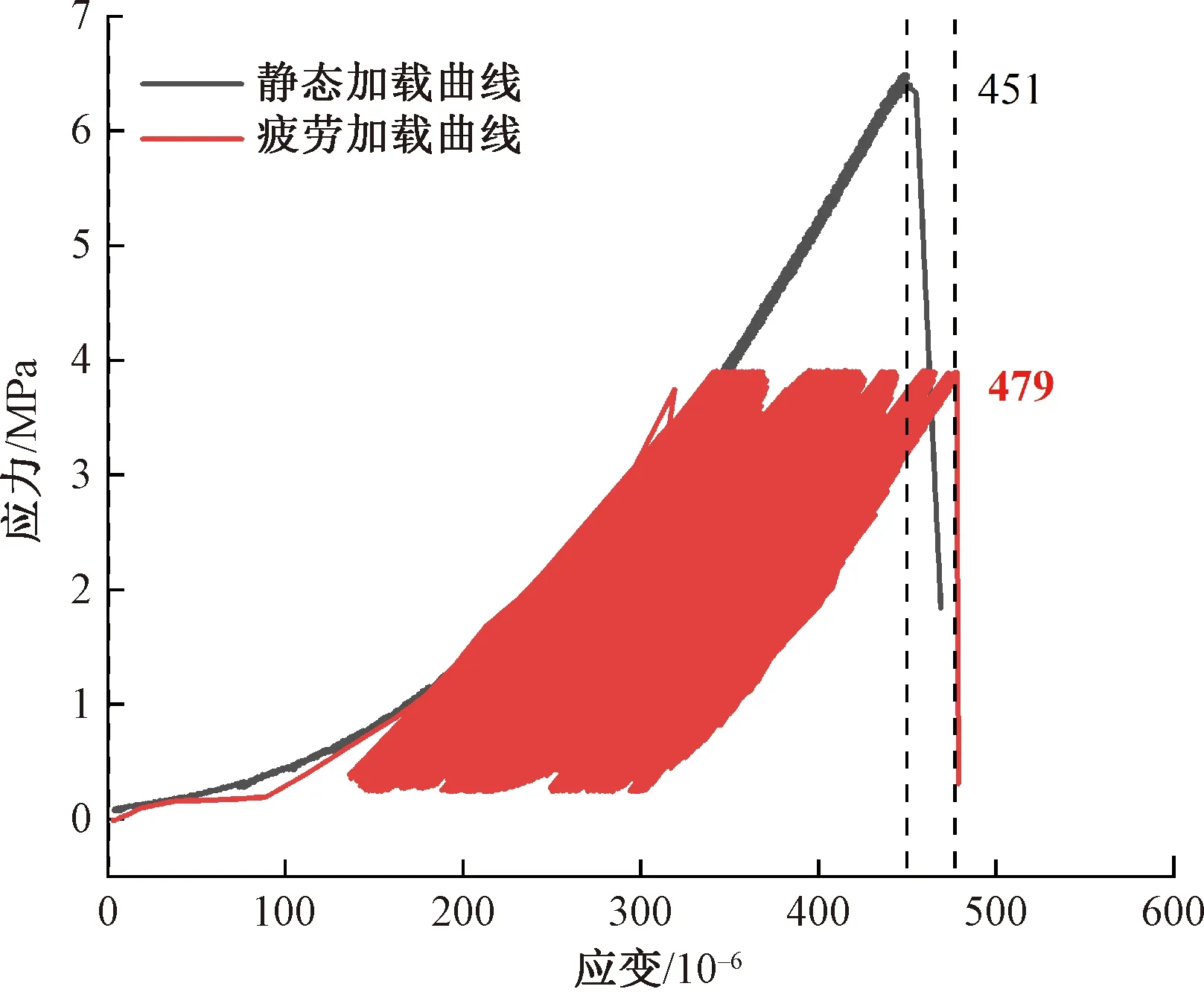
图4 静态加载与疲劳加载应力-应变曲线

疲劳加载过程中,混凝土产生位移,图5显示了混凝土试件的跨中位移与疲劳循环比的关系。疲劳荷载作用下,混凝土位移变化同样呈现三阶段的发展规律,但第一阶段对应的疲劳加载次数仅为10 000次左右,小于损伤变量第一阶段内疲劳循环次数,在该阶段内位移增长迅速;第二阶段对应的疲劳加载次数约占疲劳寿命的90%,基本对应了疲劳损伤变量的第二阶段,该阶段内混凝土位移保持相对稳定;第三阶段为位移不稳定发展阶段,呈现出阶梯式发展特征,与疲劳损伤变量的第三阶段相对应,约占疲劳寿命的10%。疲劳加载过程中混凝土位移出现三次快速上升,第一次为疲劳荷载刚开始作用时,第二次发生在疲劳循环比约为0.91时,第三次发生在疲劳破坏之前,此时裂缝突然出现并快速发展导致试件破坏。混凝土试件位移主要发生在疲劳作用后期,这与文献[23]结论相同,但其变化并不完全对应疲劳损伤变量的发展规律,没有反映出混凝土疲劳破坏第一阶段和第二阶段内部微观损伤累积情况。

图5 疲劳荷载作用下混凝土跨中位移

结合混凝土位移与开裂的情况可知,位移和裂缝在疲劳损伤的第三阶段出现突变,但此时混凝土内损伤累积明显,宏观裂缝一旦形成即在短时间内贯穿试件发生破坏,因此传统基于“不裂不疲”的工程理念对混凝土疲劳性能进行评价的方法有一定的局限性。基于冲击弹性波波速的评价方法精度较高,能够量化混凝土内部因疲劳加载而导致的损伤累积情况,且不同阶段损伤变量变化规律性良好,可用于铁路高强混凝土的疲劳性能评价。

2.3 强度等级和饱水状态的影响

2.3.1 不同强度等级混凝土

图6为不同强度等级混凝土疲劳加载后冲击弹性波波速及损伤变量变化规律。由图6可知,混凝土强度越高,初始冲击弹性波波速越高,且波速均在疲劳荷载作用下不断降低,C1混凝土(28 d抗压强度48.4 MPa)平均波速由4 514 m/s降低至4 031 m/s,下降幅度为10.7%;C2混凝土平均波速由4 682 m/s降低至3 958 m/s,下降幅度为13.4%;C3混凝土(28 d抗压强度80.1 MPa)平均波速由4 763 m/s降低至4 108 m/s,下降幅度为13.7%。三组混凝土疲劳破坏时平均损伤变量随强度增大而增大,分别为0.202、0.226和0.260。

图6 疲劳加载下不同强度等级混凝土冲击弹性波速及损伤变量

在微-细观尺度上,水泥水化产物和微观结构决定了基体及砂浆-骨料界面的力学性能,也是决定混凝土疲劳微裂纹萌生-发展和扩张的主要因素[24]。图7为三种强度混凝土疲劳破坏断面形态,图8为三种强度混凝土抗折应力-应变曲线。

图7 不同强度等级混凝土疲劳破坏断面特征

图8 不同强度等级混凝土抗折应力-应变曲线

由图7可知,混凝土断面主要包括三种情况:骨料断裂、浆体断裂和砂浆-骨料界面断裂。混凝土强度越低,砂浆-骨料界面断裂比例越大,C1和C2混凝土砂浆骨料界面断裂面积占总截面积的比例约为7.1%和4.3%,且混凝土强度等级越低,断裂处面积占比越大;而高强C3混凝土基本没有发生砂浆骨料-界面断裂。由图8可知,混凝土最大应变随抗压强度的增大而降低,峰值应力对应的应变分别为469×10-6、445×10-6、409×10-6。将应力-应变曲线下积分总面积作为单位体积混凝土吸收的能量,可知三种混凝土吸收能量分别为4.58、4.77、6.26 kJ/m3,表明混凝土强度越高吸收的能量越多。疲劳寿命随其强度的提高而增加,分别为846 547、1 019 220、1 248 451次。综合考虑能量吸收、破坏断面与损伤变量可知,随着混凝土强度增加,疲劳导致的损伤不仅会发生在浆体与砂浆骨料界面,还会越来越多地在骨料内部累积,这导致了损伤变量的上升,宏观表现为混凝土吸收能量的能力提高,混凝土承受疲劳荷载的能力得到明显提升。

试验结果表明,不同强度等级混凝土损伤变量的变化存在差异,但其发展规律与趋势相近,且能够反映出混凝土内部因疲劳加载而导致的损伤累积情况。因此,该方法对不同强度等级混凝土具有较好的适用性。

2.3.2 不同饱水状态混凝土

图9为不同饱水状态下C2混凝土疲劳加载后冲击弹性波波速及损伤变量发展规律。

图9 不同饱水状态混凝土疲劳荷载作用下冲击弹性波速及损伤变量

由图9可知,30 ℃烘干、室温和饱水三种状态的混凝土冲击弹性波波速随疲劳加载呈现下降的趋势。随着疲劳作用循环比的增加,烘干状态混凝土平均波速由4 611 m/s降低至4 051 m/s,下降幅度为12.1%;室温状态混凝土平均波速由4 682 m/s降低至3 958 m/s,下降幅度为13.4%;饱水状态混凝土平均波速由4 676 m/s降低至4 104 m/s,下降幅度为12.2%。不同饱水状态下冲击弹性波波速与损伤参数变化规律相近,规律性良好,破坏前损伤变量均约为0.230。

图10为不同饱水状态下C2混凝土疲劳寿命变化情况。由图10可知,混凝土在烘干、室温和饱水三种状态下的疲劳寿命分别为904 502、1 019 220、956 802次。结合图9可知,不同饱水状态下冲击弹性波波速存在差异,原因是混凝土内部存在微观孔隙和微裂缝。当处于完全饱水状态时,水充满了尺寸较大的孔隙,动态作用下孔隙中水压导致了裂缝扩展和损伤发生,使得混凝土的性能劣化。Yaman等[25]研究得出随着孔隙率和孔隙中含水量的增加,孔隙水压增加,混凝土的抗压强度、弹性模量都呈现逐渐降低的规律。干燥状态下孔隙间水分减少,孔隙水的黏性作用降低,减弱了孔隙水对浆-骨界面之间相对运动的阻止作用,导致在动态荷载作用下混凝土损伤更加明显。

图10 不同饱水状态混凝土疲劳寿命

2.4 铁路混凝土疲劳临界状态确定

根据试验结果可知,不同试验条件下混凝土均在损伤变量达到0.2后迅速发生疲劳破坏。图11为C2混凝土疲劳加载后强度损失情况。由图11可知,混凝土剩余抗折强度随疲劳加载出现明显的单调衰减趋势。在疲劳作用循环比达到0.8之前,混凝土强度损失较慢且基本呈现线性关系,其强度衰减系数小于0.15,对应的损伤变量小于0.1,处于稳定发展的第二阶段。而当疲劳作用循环比达到0.8后,混凝土剩余强度迅速降低。疲劳作用循环比达到0.96后混凝土强度降低了0.38,强度衰减已经十分明显,此时对应损伤变量值为0.2,且处于不稳定快速增长的第三阶段。

图11 不同疲劳循环比混凝土剩余抗折强度与损伤变量

由图11可知,前两阶段混凝土性能损失与损伤变量变化均较小且变化不明显。若疲劳损伤判据过低(小于0.1),则无法准确判断混凝土疲劳损伤状态。铁路预应力构件混凝土强度等级多为C50及以上等级,在内部能量累积到一定程度后可能发生突然断裂。同时,铁路混凝土除受列车荷载外,还会因环境侵蚀、冻融循环等多因素耦合作用造成服役性能下降。若疲劳损伤判据过高,则可能会影响混凝土疲劳性能的评估与疲劳寿命的预测。因此,综合本文试验结果与疲劳破坏第三阶段突变特征,建议将0.2确定为铁路混凝土疲劳损伤的临界状态。

3 结论

(1)静态加载下不同混凝土冲击弹性波波速及其损伤变量随荷载率增加呈现上升趋势,冲击弹性波波速可以反映因加载导致的混凝土内部累积损伤变化情况,混凝土抗折加载损伤变量变化比抗压加载更明显。

(2)冲击弹性波波速及其损伤变量能够反映混凝土疲劳损伤的三个特征阶段,每阶段所占疲劳寿命比例基本相当,不受加荷频率影响。疲劳荷载作用下损伤变量发展规律性良好,且与混凝土宏观位移变化趋势一致,基于弹性波波速的疲劳损伤评价方法可用于混凝土疲劳损伤评价。

(3)随着强度等级提高,混凝土发生疲劳断裂时的损伤变量逐渐增加大,其原因是高强混凝土浆骨界面黏结力强,破坏时吸收能量大;含水率影响了混凝土疲劳损伤变量,饱水及干燥状态均降低了混凝土疲劳寿命。

(4)混凝土的剩余抗折强度及损伤变量存在相似的拐点,表明该方法可以反映混凝土在疲劳过程中的宏观性能变化特征。基于疲劳损伤第三阶段突变特征,建议将损伤变量0.2作为混凝土疲劳损伤的临界状态。