在多元表征中促进算理算法的融通——“笔算除法”的思考与实践

□蒋康丽

一、找学生起点——统计与分析前测数据

教学人教版教材三年级下册“除数是一位数”单元“笔算除法”时，为了解学生的学习起点，把握学生的认知水平，笔者对任教班级45 名学生进行了前测。前测试题由两道题目构成，具体如下。

（一）了解学生解决除法问题时的多种方法

前测题目1：将45 根小棒平均分成3 份，你打算怎么分？请你一边摆小棒一边用语言进行说明。

具体测试结果包括：

（1）先分十位上的整十根，再分个位上的，最后将十位和个位上剩余的合起来一起分。即先从40里面拿出30分成（10，10，10），再从5里面拿出3分成（1，1，1），最后将剩余的10+2=12 分成（4，4，4），结果为每份10+1+4=15（根）。使用这种分法的学生约占总人数的33.33%。

（2）先分十位上的整十根，再把十位和个位上剩余的合起来一起分。即先从40里面拿出30分成（10，10，10），接着将剩余的10+5=15分成（5，5，5），结果为每份10+5=15（根）。这种方法是教材中引出除法竖式的方法，使用这种方法的学生约占总人数的28.89%。

（3）先分个位上的，再十位上退一作十和个位上剩余的合起来一起分，最后分十位上剩余的整十根。即先从5里面拿出3分成（1，1，1），再把10+2=12 分成（4，4，4），最后将剩余的30 分成（10，10，10），结果为每份1+4+10=15（根）。使用这种分法的学生约占总人数的17.78%。

（4）先分个位上的，再分十位上的整十根，最后将十位和个位上剩余的合起来一起分。即先从5里面拿出3分成（1，1，1），再从40里面拿出30分成（10，10，10），最后将剩余的10+2=12分成（4，4，4），结果为每份1+10+4=15（根）。使用这种分法的学生约占总人数的8.89%。

（5）将全部小棒拆开1 根1 根分，即将45 根小棒按（1，1，1）分15 次。使用这种分法的学生约占总人数的4.44%。

（6）约6.67%的学生没有进行操作。

其中，第（1）和第（2）种方法体现了从高位算起，第（3）和第（4）种方法体现了从低位算起。由此可见，学生具备解决问题的多种方法，如果教师直接使用第（2）种方法引出除法竖式，就只符合部分学生的认知，并未完全立足真实的学情。

（二）了解学生用除法竖式进行计算的起点

前测题目2：用竖式计算45÷3。

测试结果显示：45名学生中，计算过程与结果均无误的只有10 人，约占总人数的22.22%，他们已经初步掌握了两位数除以一位数的笔算方法；15名学生能得到正确的商，但笔算格式有误，约占总人数的33.33%；有20 名学生的答案与计算过程均有误，约占总人数的44.44%。笔者对学生错误的原因进行分析（如表1），发现主要有以下几种：未理解竖式计算的价值，将口算等同于竖式；虽然已有试商的意识，但不敢挑战两次试商或两次试商后不知如何处理各组成部分的位置；不懂算理，未将被除数的拆分与除法运算算理联系起来。

二、析学生所难——分析“笔算除法”之所以难的原因

（一）知识的负迁移导致理解的困难

从形式上看，笔算除法的书写形式与学生已学的笔算加法、减法、乘法的书写形式有很大的不同。笔算加法、减法、乘法的书写形式从低位算起，从上往下依次计算；笔算除法的书写形式从高位算起，并将计算结果写于被除数的上方。从运算的复杂性看，加法与减法仅是基于计数单位的运算；乘法则需要在拆分乘数的基础上，利用乘法口诀和加法进行组合运算；笔算除法则需要在拆分被除数的基础上，综合运用加法、减法和乘法三种运算，且这样三种运算合一的竖式模型较难纳入学生原有的认知结构中。从与“有余数除法”的联系上看，在学习“有余数除法”时，学生已经有了除法竖式的初步模型，这种初步模型只需要用乘法口诀就可以直接求商，但这种方法很难直接迁移到“笔算除法”中，因此学生不敢挑战两次试商或两次试商后不知如何处理各部分的位置。

（二）从试商的多样化到标准竖式的跨越难度大

得出除法计算结果的方法有多种，但标准竖式背后的试商只有一种，就是通过试商将被除数拆分成能被除数整除的最大整十数以及被除数和这个最大整十数的差，如计算75÷3，要将75 拆成60 和15。试商的本质就是利用乘法运算对被除数进行拆分，试商过程是帮助学生理解算理的过程，标准竖式书写则是对运算方法的优化。如何让学生在理解算理的基础上掌握算法是一个有着逻辑关联的过程。

三、构教学活动——深度理解笔算除法

通过上述调查与分析，要突破“笔算除法”这一教学难点，可以尝试在学生多样的分小棒方法的基础上，建立试商与除法竖式的联系，让学生在动作表征、图式表征、竖式表征的关联中理解算理、掌握算法。同时，考虑到分小棒的动作表征起点较低，教学目标定位为在充分理解算理基础上初步掌握算法。因此，笔者对教学进行了单元整体设计，直接从退位的笔算除法开始，将长竖式引入教学。具体的教学活动如下。

【片段1】实物操作，初步感知

师：将45根小棒平均分成3份，你打算怎么分？

生：1根1根地分。

师：有没有方便一些的分法？

生：我是这样分的，10根小棒扎成1捆（下同），先分整捆的小棒，每份1捆，剩下1捆；再分单根的小棒，每份分1根，剩下2根；最后把剩下的1捆拆开，和刚才剩下的2根合成12根小棒继续分，得到结果。

生：我的方法是先分整捆的小棒，每份1捆，剩下1 捆；再把剩下的1 捆拆开，和另外5 根合成15根小棒继续分，得到结果。

生：我是先分单根的小棒，每份1根，剩下2根；再拆1 捆小棒，与2 根合在一起，每份获得4 根；最后分整捆，每份获得1捆。

【片段2】图式表征，深入感知

教师将学生分的过程记录在黑板上（小棒图），如图1所示。

图1

接着组织学生讨论：比较三种分法，它们有什么相同点与不同点？

（1）分法②与分法③都是先分整捆再分零散的，分法①是先分零散再分整捆的。

（2）分法③两次分完，分法①与分法②则要分三次。

设计意图:分小棒的过程，就是运用运算律理解算理的过程。学生在叙述分的过程时，自然地运用语言进行描述，虽然不严谨、不简练，但是已经能描述和概括出具体的操作活动。除此之外，学生还从中体会到整捆分的好处以及拆开剩余1 捆小棒的必要性。

【片段3】竖式化表征，追本溯源

1.自主探究用竖式记录分的过程

（1）教师出示任务：请大家自主探究用竖式记录图1中分法②的分小棒过程。

师：你们能用竖式的形式将图1中分法②的分小棒过程记录下来吗？

（2）呈现学生作品。教师巡视发现，大部分学生列的竖式为“一层楼”式，如图2所示。

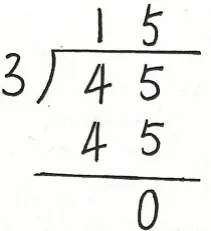
图2

（3）同桌讨论：你能看明白他列的竖式吗？你赞同他的写法吗？

生：这种写法只呈现了最终答案，没有将这三次分小棒的过程一一记录下来。

2.合作探究用长竖式记录分的过程

（1）在师生对话中生成除法的长竖式，结合小棒图介绍长竖式各部分的含义，结合数学史进行数学文化的熏陶。

（2）通过图式表征、竖式表征和语言描述，帮助学生理解笔算除法的算理和算法（如表2）。

表2

3.巩固练习，举一反三

教师出示任务要求：请大家在图1中剩余的两幅小棒图中任选一幅，将整个分小棒的过程用像这样的长竖式记录下来。

图3 中竖式各部分的含义：45 指的是共有45根小棒，3表示平均分成3份，10表示第一次每份分到10 根。第一次一共分掉了30 根，还剩15 根；第二次每份分到5根，一共分掉了15根，没有剩余。

图3

图4 中竖式各部分的含义：45 指的是共有45根小棒，3 表示平均分成3 份，1 表示第一次每份分到1 根。第一次一共分掉了3 根，此时还剩下42根；第二次每份分到4 根，一共分掉了12 根，还剩30根；第三次每份分到10根，一共分掉了30根，没有剩余。

图4

设计意图：学生在寻求简练的记录方式的过程中，感悟到分小棒的过程与竖式记录方式之间的联系，渗透了数形结合思想，建立了竖式模型。同时，学生在探究中运用数学语言来描述，切实感受到竖式产生和应用的价值。这样既满足了学生的好奇心，也使学生积累了探究的经验，更增强了学生追本溯源的意识。

【片段4】对照比较，逐步优化

教师出示任务：请大家观察表2和图3、图4中的长竖式，比较它们有什么相同与不同之处。

（1）表2与图3中的两个长竖式中，第一次的商都为10，这是因为它们第一次都是先分的整捆，从算法上来讲都是先算十位。也就是说，这两个长竖式都是从高位算起的。

虽然这两个长竖式第一次的分法相同，但第二次的分法就不同了。图3 是在分完第一次后将剩余的部分也就是1 个十和5 个一合起来一起分，每份分到5根；而表2是在第一次分了整捆后，第二次再分根，最后将捆的剩余根数与零散的根数合起来一起分。

对比发现：图3 中的长竖式较为简单，从竖式运算上看，捆分完后，剩下的捆和根合成的数除以除数是一个简单的表内除法问题。

（2）图4 中的长竖式第一次分，每份分到1 根，而表2 和图3 中的两个长竖式第一次分，每份都分到10根。从小棒图来看，这一种分法是先分根的，从算法上来讲就是先算个位。

对比发现：表2 中的长竖式可以简化为图3 中的长竖式，而图4中的长竖式（从个位算起）则无法缩简。

总结：除法从高位算起。

设计意图：通过对比几种竖式计算方法，学生能感悟到竖式除法确立的过程。通过不断探索，竖式得以不断简化，多样的顺序慢慢统一，琐碎的步骤慢慢压缩，多余的符号慢慢消除，不同的写法慢慢规范。

四、思教学过程——多元表征，理法融通

单元整体设计视角下的“笔算除法”从动作表征入手，建立了图式表征和竖式表征，让学生在图式表征与竖式表征的关联中理解笔算除法的意义和算理，在图式表征与竖式表征的对比中经历笔算除法的简化过程，初步掌握算法。

（一）多元表征的关联促使学生形成完整的思维链条

从分小棒操作到得出标准竖式是一个非线性的过程。前测表明，学生已具备多种分小棒的方法，也能运用多种方法试商。因此，教学时要通过多元表征及表征之间的联系，促使学生深度思考，形成完整的思维链条。具体而言，分小棒的多种方法及对应的图式表征、竖式表征确保了学生思考的充分性和一致性，分小棒的动作表征及分小棒过程的图式表征则实现了均分过程的思维外显。通过图式表征可以知道每一步分到了什么，而运用竖式表征可以体现运算过程中的“每一步怎么分、分了什么、分到了什么、剩下什么”，使外显的思维建立联系，完整地呈现出对应图式表征的过程，最终形成思维链条。

（二）长竖式的引入促成算理和算法的融通

在以往的教学中，教师也会关注动作表征和图式表征，但往往是通过从这两种表征直接过渡到标准竖式表征，从而帮助学生理解除法竖式的意义和运算的一致性。但这样的教学仅仅关注了学生思考的一致性而忽略了学生思考的充分性，忽视了学生的认知基础——试商，不利于学生理解算理。本内容的教学充分认识到竖式的价值，将分小棒的过程完整地记录下来，并引入了长竖式。一方面，让多种动作表征及对应的图式表征有了进一步表征的机会，实现思考的充分性；另一方面，通过对多种竖式表征的对比，使学生理解竖式的意义与算理，经历竖式的简化过程，认识到用标准竖式表征的必要性。

（三）单元整体设计让教学路径更为合理

“除数是一位数的除法”单元中的“笔算除法”涉及被除数是两位数、被除数是三位数和有关0的除法，共编排了7 个例题、10 道不同类型的除法运算。从编排的逻辑来看，是从易到难、从特殊到一般再到特殊，注重退位除法与被除数或商中有零的除法等难题的解决。事实上，无论是教学哪类整数除法，让学生理解算理、掌握算法是关键。因此，笔者从单元整体设计的视角出发，调整教学路径，搭建长竖式这一学习支架，让长竖式贯穿整个“笔算除法”教学：第1 课时让学生借助长竖式理解除法竖式记录“分的过程”的功能，第2课时让学生经历长竖式到标准竖式的简化过程。具体围绕例6“（1）208÷2”与例7“（1）650÷5”、例6“（2）216÷2”与例7“（2）245÷8”安排2 个课时的教学，引导学生用长竖式来理解标准竖式的书写道理。由此，教师充分利用长竖式这一学习支架，让学生在理解算理的基础上，更好地掌握各类整数除法的算法。