“平行四边形的面积”教学中的问题分析

□江 燕 郜舒竹

一、以“拉一拉”活动作为导入方式的不合理性

在现有“平行四边形的面积”的教学设计及课堂教学中，有教师会在导入环节采用“拉一拉”的操作活动［1］，让学生通过拉动长方形模型，感知长方形被拉动后变成了平行四边形，并将拉成的平行四边形与原有的长方形作对比，发现图形周长相等，面积却在变小。将“拉一拉”这一操作活动作为本课的导入方式是否合适，值得深度思考。

首先，北师大版教材将面积定义为“物体的表面或封闭图形的大小”。面积是对“面”的大小的度量，“面”的存在是计量面积的前提。在“拉一拉”的操作活动中，从视觉角度看，学生能观察到图形相邻两条边之间的相对位置在改变，却不能直观地观察到“面”这一属性。没有“面”作为前提，也就无从感知图形面积（“面”的大小）在逐渐变小。

其次，如图1所示，捏住长方形模型ABCD的一组对角向外拉，当长方形ABCD变为平行四边形A'B'C'D'时，多数学生会认为长方形ABCD的面积与平行四边形A'B'C'D'的面积相等，理由是向斜角凸出的部分（增加的量）和向下减少的部分（减少的量）相等，根据“量1加上量2，又减去量2，结果仍为量1”的事实，可以得出长方形ABCD与平行四边形A'B'C'D'具有“形异量等”的等价关系，二者面积相等。

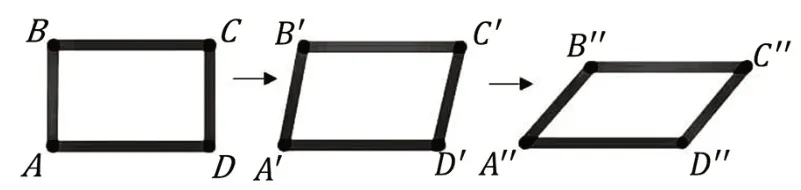
图1 长方形被拉动后变成平行四边形示意图

此外，学生在三年级时已获得“长方形的面积=长×宽”的认知。从视觉上看，长与宽是长方形相邻两边的长度，因此学生容易形成“长方形面积等于相邻两边长度乘积”的错误图式。在“拉一拉”的操作活动中，拉动的过程改变的是相邻两边之间的相对位置，边的长度并未改变，所以长方形ABCD相邻两边的长度与平行四边形A'B'C'D'相邻两边的长度相等。利用有关长方形面积的认知经验，学生自然而然就形成了“平行四边形的面积等于相邻两边长度乘积”的直觉错误。只有当长方形ABCD被拉成比较扁的平行四边形A''B''C''D''时，学生才能直观地发现图形的周长没有变化，面积却在变小。

要解决学生在“拉一拉”操作活动中无法直观感知到“面”这一问题，以及形成“平行四边形的面积等于相邻两边长度乘积”的直觉错误，就必须了解“面”这一属性，同时澄清长方形ABCD与平行四边形A'B'C'D'面积不相等。为此可以采用几何动画的形式，如图2所示，以动态的眼光去看，拉动的过程实际就是长方形旋转导致形变（变为平行四边形）的过程，直观来看就是长方形的宽沿顺时针方向旋转一个角度，此时边长保持不变，但面积变小了，而且随着旋转的继续，面积会越来越小。

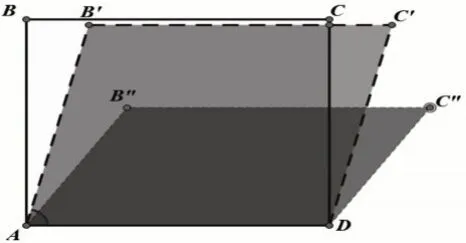
图2 长方形旋转为平行四边形示意图

最后，通过“拉一拉”操作活动，学生得出结论：长方形被拉成平行四边形后，其面积在变小，即此时的长方形和平行四边形之间存在“形异量不等”的关系。然而，在推导平行四边形的面积时，学生是通过“分、移、补”的活动将平行四边形转化为长方形，再借助已知长方形的面积计算公式去推导平行四边形的面积计算公式的。此时学生得出的结论为平行四边形与长方形的面积相等（如图3），即此时的长方形和平行四边形之间存在“形异量等”的关系。可见，学生在两个活动中所得出的结论并不一致，这会导致他们思维混乱，无法真正理解平行四边形的面积与长方形的面积之间的内在关系。

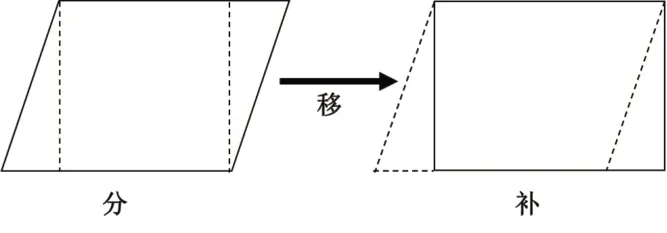
图3 平行四边形转化为长方形示意图

对于“拉一拉”这一操作活动，人教版教材五年级上册“平行四边形的面积”将其以课后习题的形式放置于练习十九中（如图4）。此前，学生通过对教学内容的学习，已经明晰平行四边形的面积受到底和高的制约，是底和高的乘积；同时“分、移、补”活动使学生认识到，平行四边形的面积与长方形的面积相等的原因在于图形间的内部因素具有一一对应的关系，即原有的平行四边形的底与高分别转化成了长方形的长和宽。基于以上认知经验去解释和说明为什么在拉动过程中图形的面积在变小，就能避免“平行四边形的面积等于相邻两边长度乘积”的直觉错误以及结论不一致导致的思维混乱。

图4 教材中与“拉一拉”操作活动相关的练习题

综上所述，将“拉一拉”操作活动作为“平行四边形的面积”教学的导入方式，有如下弊端：一是无法保证度量面积的前提——“面”这一属性的存在；二是当捏住长方形的一组对角轻轻拉动时，学生通过直接观察模型，无法直观地感知面积的变化（变小），因而会认为此时图形的周长和面积都没有发生变化，再结合对长方形面积的认知，产生“平行四边形的面积等于相邻两边长度乘积”的直觉错误；三是“拉一拉”操作活动中平行四边形与长方形之间呈现的“形异量不等”关系，与后续“分、移、补”活动中平行四边形与长方形之间呈现的“形异量等”关系相互冲突，知识内容的不一致会导致学生思维混乱。

二、“数方格”法的片面化看待和不科学规定

面积计量的一个基本方法是单位面积度量法，在小学数学中通常也叫作“数方格”法。该方法是将一张方格纸当作一把“面积尺”（其中每个方格代表一个面积单位），通过将平面图形平铺于方格纸上，数出图形含有多少个方格（面积单位的个数），以此计算图形的面积。［2］在有关面积内容（包括平行四边形的面积）的教学中，初始时一般都会采用“数方格”的方法来进行。但在部分“平行四边形的面积”的教学设计中，教师认为“数方格”的方法既不好操作，又很烦琐，与之相比，剪拼的方法易于操作且方便，因此直接摒弃“数方格”的方法，强调引导学生将平行四边形通过剪拼的活动转化为长方形来计算面积。［3］

那么，“数方格”法在面积教学中是否重要呢？“图形与几何”领域中涉及许多有关图形面积计量（平面图形的面积以及立体图形的表面积）的内容。史宁中教授认为，面积度量实质就是计算该图形包含多少个面积单位。［4］“数方格”是以方格纸作为度量面积的直观模型，其实质就是“数”面积单位的个数，所以借助“数方格”的方法可以帮助学生理解面积是面积单位的累加，计量面积就是计量面积单位的个数。

人教版教材中仍然沿用“数方格”这一方法。在数格子的过程中，学生会遇到所数“方格”不是“整格”的情况。对此，教材的解决办法是：不满一格的都按半格计算（如图5）。

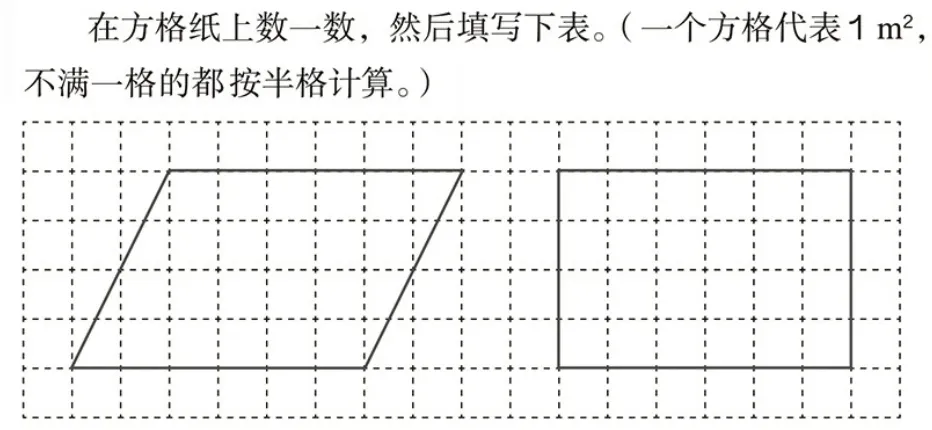
图5 教材中“数方格”的规定示意图

然而，在实际应用中，那些不满一格的“方格”，有些与一格十分接近，有些非常小（甚至可以忽略），全都把它们按半格计算的做法具有合理性吗？

如图6 所示，图中两个平行四边形的形状不同，但底边长度和高度分别相等。已知决定平行四边形的面积的因素是底和高，所以底和高分别相等的平行四边形的面积相等，即图6中两个平行四边形的面积相等。再根据平行四边形面积=底×高，可以计算出两个平行四边形的面积都为2×2.5=5（平方厘米）。

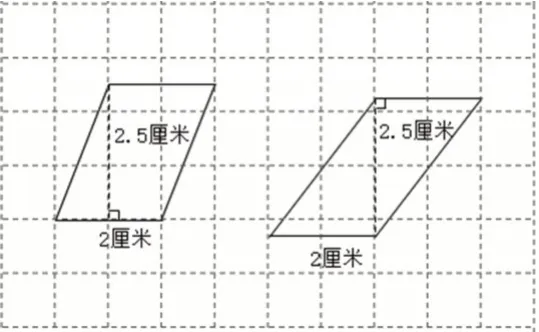
图6 方格纸中底与高相等的两个平行四边形示意图

如果采用“数方格”的方法，可以数出图6左边的平行四边形有2个“整格”，“不满一格”的有7个；右边的平行四边形有2个“整格”，“不满一格”的有10 个。按照“不满一格的都按半格计算”的规定，左边的平行四边形包含2 个“整格”和7 个“半格”，右边的平行四边形包含2个“整格”和10个“半格”。1 个方格代表1 平方厘米，半格就代表0.5 平方厘米，从而数出左边平行四边形的面积为5.5 平方厘米，右边平行四边形的面积为7平方厘米。

显而易见，按照“不满一格的都按半格计算”的规定，“数”出来的面积数与实际面积数之间存在不一致性，而且还是一个具有不确定性的估计值，形状不同，数值也不同。因此，将“不满一格的都按半格计算”的做法不科学、不严谨、不具合理性，学生难以接受。如果换个角度去引导学生思考：不采用“不满一格的都按半格计算”的做法，那“整格”以外的方格（接近一格与不足半格或两个半格）应该怎么计量？学生结合生活经验，可能会想出通过剪拼的方式，将不足一格的方格拼在一起变成“整格”来计量，在此基础上自然而然地引出转化思想以及实现转化的方法——剪拼法，从而建立“数方格”法与“转化”之间的深度联系。

除此之外，借助方格纸的直观性进行“平行四边形的面积”的教学，能帮助学生明确底和高是决定平行四边形的面积的关键因素，并根据直观得到的平行四边形面积、底和高之间的关系，推导出平行四边形的面积=底×高，从而实现数形结合。如图7所示，将三个不同形状的平行四边形复刻于方格纸上，利用方格纸的直观性，比较它们的底、高、面积之间的关系。比较图①和图②，可知平行四边形的高相同，底越长，面积越大；比较图②和图③，可知平行四边形的底相同，高越长，面积越大。因此得到决定平行四边形面积的关键因素为底和高。

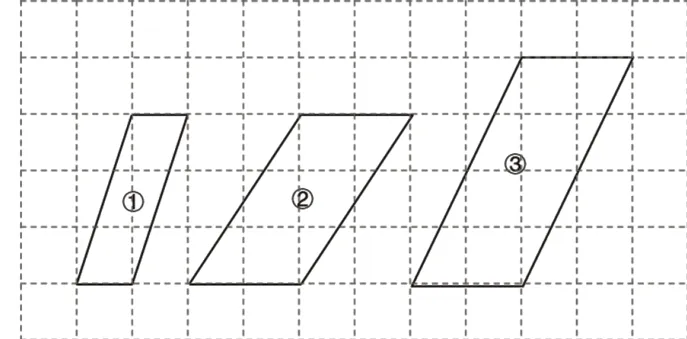
图7 方格纸上三个不同形状的平行四边形示意图

同样，在图5提及的方格纸中，一个方格代表1平方米，边长为1米的正方形的面积为1平方米，即每个方格的边长为1 米。学生结合方格图可以直接数出三个平行四边形的面积、底和高，并通过将三个不同形状的平行四边形的面积与其对应的底和高的乘积进行比较，在数形结合中发现规律：平行四边形的面积受制于底和高，是底和高的乘积。

三、“分、移、补”活动中结论和剪拼方式的不完备

对于“平行四边形的面积”的推导，教材中多是引导学生通过“分、移、补”的活动，沿着高从平行四边形中分出一个直角三角形，将其平移到另一侧，然后补齐变成长方形（如图3），此时平行四边形的底转化为长方形的长，高转化为长方形的宽，结合“长方形的面积=长×宽”，推导出“平行四边形的面积=底×高”。但教材中这样的设计指向的只是一个特殊的平行四边形的面积，其高位于平行四边形内部（以下简称“形内高”），而对于高位于形外（以下简称“形外高”）的情况却并未涉及［5］。

“形内高”平行四边形转化为长方形的方式是将左边的直角三角形剪下来平移到右边对应的位置。然而这种剪拼转化的方法，对于“形外高”平行四边形来说并不适用（如图8）。

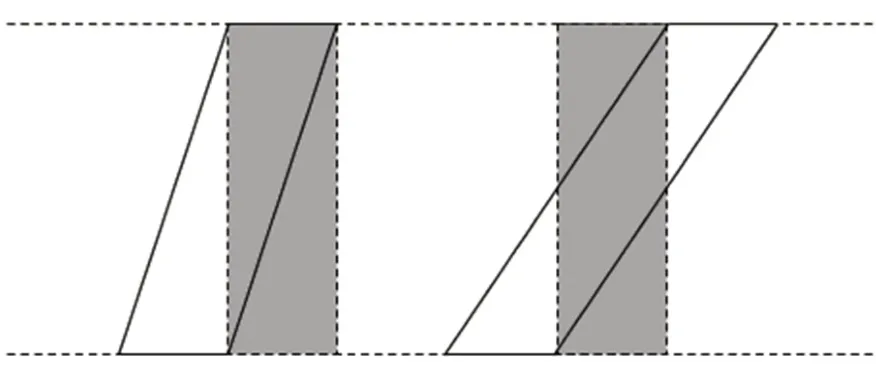
图8 “形内高”“形外高”的平行四边形转化为长方形示意图

对此，学生会产生“是否平面上每一个平行四边形都可以转化为长方形？”“同一个平行四边形具有不同的底边和对应的高，其面积是否都可以用底与高的乘积来表示？”“所有的平行四边形都是沿着高分割出一个直角三角形，平移到另一侧，补齐成长方形吗？”等疑惑。

因此，只针对“形内高”平行四边形得出“平行四边形的面积=底×高”的结论，在一定程度上会缺乏说服力。且将其转化为长方形的过程中只涉及“将左边的直角三角形平移到右边对应的位置”的剪拼方式，可能会忽视学生自主构建多样化的转化方法的可能性。所以，教师应该尽可能提供多角度的材料，让学生观察、操作、思考，发现不同角度、不同形状、不同大小的平行四边形（包括“形内高”和“形外高”）都可以通过剪拼的方式转化为长方形，剪拼的方式可以是多样化的。在此基础上根据平行四边形的面积（底乘高）与转化后的长方形的面积（长乘宽）之间建立等价关系，结合“长方形的面积=长×宽”的知识经验，得到“平行四边形的面积=底×高”。这种让学生对不同类型的平行四边形进行剪拼，并由一定的知识经验得出的结论，才能让学生体会到转化方法的多样性及结论的科学性、合理性。因此，我们要对“平行四边形的面积”的教学进行重新认识，设计出科学、合理并有益于学生数学核心素养发展的学习活动。