数学文化融入数学教学的实践与思考
魏小梅
【摘要】《中等职业技术学校数学课程标准》指出,数学课程承担着立德树人的根本任务.这对五年制高职数学课程提出了新的挑战.基于此,文章从數学文化的视角出发,以“计算球的体积”为例,从创设情境、巧设模型、穿越历史、提升能力四个方面进行了教学设计,探究了五年制高职数学文化与数学教学相融合的实践与思考,以期为高职数学教师将数学文化融入数学教学提供思路.
【关键词】数学文化;立德树人;数学教学.
【基金项目】常州卫生高等职业技术学校2021校级课题:基于中职数学课程标准下的“三融三乐”课堂的教学实践研究(课题编号:CW202103).
数学课程作为五年制高职学校各专业学生必修的公共基础课程,承载着立德树人的根本任务,具备发展素质教育的功能.对学生而言,这一阶段正是人生观、价值观形成的关键时期,所以教师要发挥其示范引领作用,培养具有社会主义核心价值观的高素质技能人才.传统的数学课堂教学更注重数学知识的传授和理性思维的推演,而忽略了数学本身所具有的文化属性.因此数学课程的育人功能一直都是短板,需要广大教师进行深入的思考和探索.例如,“立体几何”中柱体、锥体及球的体积计算公式,教材是直接给出的,并没有证明过程,仅仅在“读一读”中介绍了祖暅原理,并说明了祖暅原理的作用及在世界数学史上的地位.事实上,学生如果仅仅是读一读,收获并不大,反而容易产生更大的疑问:祖暅原理是怎么解决几何体体积的计算问题的.为了解决球的体积的计算问题,同时为了弘扬中国古代优秀的数学文化,笔者对这部分知识进行了重新设计与反思.
一、教学设计
(一)创设情境,引入问题
师:课前我们布置了一份特别的作业,观看一场奥运会乒乓球比赛,测量一个标准乒乓球的体积(不允许用球体体积公式).请大家说说你的测量结果.
生1:我是利用排水实验来测量球体积的.先准备一大一小两个水杯,小水杯里注满水放置在大水杯里,将一个乒乓球轻轻地按压进小水杯中,这时小水杯中的水流入大水杯中,直到乒乓球完全浸入水中停止按压,然后将大水杯中的水全部倒入带有刻度的试管中,并记录下水的刻度,试管中水的体积就等于乒乓球的体积.通过多次反复测量,得到了一个乒乓球的体积约为32cm3.
师:这个同学的想法很好,乒乓球完全浸入水中后排出的水的体积就等于乒乓球的体积,水的体积我们可以利用试管测量.那么其他同学怎么测量的呢?跟大家分享一下.
生2:我先通过直尺反复测量获得乒乓球的直径是4cm,接着制作了一个边长为4cm的无盖正方体,将乒乓球放置其中.然后,将提前准备好的沙子缓缓倒入其中,将所有空隙填满.最后,轻轻将乒乓球取出,将留在正方体内的沙子抹平,记录其高度.那么正方体的体积减去沙子的体积就是乒乓球的体积.我测量的乒乓球的体积为33cm3.
师:大家自己动手去测量乒乓球的体积,这种勇于探索的精神值得肯定.那么,乒乓球的体积到底是多少呢?下面,我们就来球的体积计算问题.
【数学思政】在创设情境计算球的体积时,选择了极具群众基础的“国球”乒乓球,结合观看奥运会乒乓球比赛,让学生在不知不觉中感受到中国运动员的拼搏精神和爱国情怀.教师选择合适的切入点进行课程思政,在点滴中渗透中国骄傲和中国自信,可以帮助学生树立正确的人生观和价值观.数学课堂中从来都不缺乏严谨的推理,学生通过实验测量乒乓球的体积,能够初步感知球的体积计算的问题.学生通过动手测量,用眼观察,用脑思考,一步一步地激发其学习兴趣,为后面更高阶的数学思维探索做铺垫.
(二)巧设模型,猜想公式
师:球是完美的对称图形,如果能计算出半球的体积,那么也就得到了球的体积.大家观察图1中的三个图形,它们之间的体积大小有什么关系?
师:同学说得不错,这个猜想可能是对的,但是如果能严格证明的话就更好了.
(三)穿越历史,感受文化
师:说到球的体积计算问题,就不得不提我国古代著名的父子数学家祖冲之和他的儿子祖暅以及祖暅原理.请看微视频介绍.
微视频展示:祖冲之,南北朝时期杰出的数学家、天文学家,他首次将圆周率精确计算到小数点后面第七位.祖暅,祖冲之的儿子,也是南北朝时期著名的数学家、天文学家,同父亲祖冲之一起圆满解决了球体积的计算问题,并提出了著名的“祖暅原理”.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚了一千一百多年.那么什么是祖暅原理呢?祖暅原理就是:幂势既同则积不容异.幂是水平截面的面积,势即是高,翻译过来就是:夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积相等,那么这两个几何体的体积相等(如图2所示).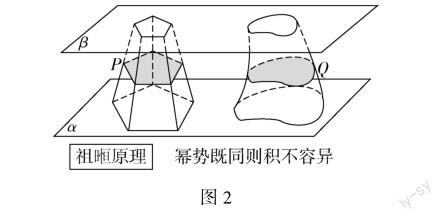
师:同学们可能还不是很理解祖暅原理,我们用实验展示一下.请一个同学上讲台来配合.
演示:先将20个硬币整齐地排成一列成圆柱形,然后再将20个硬币随意的排成一列,保证两列硬币是同样的高度,但是形状完全不同.提出问题:这两列硬币构成的几何体的体积有什么关系?
生:体积相等.
师:为什么呢?
生:这两个几何体的体积都等于20个硬币的体积之和.
师:大家的感觉都是对的,但是,数学更要讲究有理有据.祖暅原理就是给我们提供了依据,因为这两个几何体等高,而且等高处的水平截面的面积都是硬币的面积,所以相等,依据祖暅原理,这两个几何体的体积相等.
【数学思政】数学文化是进行课程思政的重要资源,其中浩瀚的数学史长河,有趣生动的数学故事和令人敬仰的数学家等,都需要教师去开发利用.结合本节的球体积公式,学生必然会提出公式怎么来的这样的问题.数学的核心在于思维,如果想要讲清楚公式怎么来的,也必须还原数学知识的来龙去脉.在这个过程中,学生深入了解中国古代数学家做出了杰出的成就,祖暅原理在世界数学发展史上也是处于领先的地位,增强学生的民族自信心.
(四)提升能力,推导公式
师:为了求半球的体积,构造了如图3所示的幾何体,同学们先观察一下,图3中的的两个几何体是否满足祖暅原理的两个条件?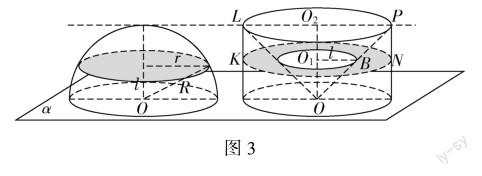

师:经过证明的公式,大家就可以放心使用了.那么我们用球的体积公式来计算一下乒乓球的体积吧?
二、教学思考
本次教学设计中加入了数学实验的活动,扭转了学生对数学只有理论没有实验的偏见.首先,教师布置课前作业:动手测量乒乓球的体积,学生在亲自操作中积累数学体验,激发对球体体积计算问题的兴趣.其次,教师选择中国体育强项乒乓球为探索对象,使学生在观看比赛中自然而然地感受到了爱国主义的氛围.最后,数学课程的任务是培养学生的数学核心素养和立德树人,这两个任务是同时进行不可分割的,培养数学核心素养是课堂的主旋律,贯穿始终,而数学课堂的育人任务则是选好时机,数学文化就是很好的载体,文化的育人功能使学生在不知不觉中接受了思想教育,达到润物细无声的境界.
数学文化是数学思政元素的天然资源库.广义的数学文化除了数学的思想、精神、方法、观点、语言,还包含数学家、数学史、数学美、数学教育、数学发展中的人文成份,数学与社会的联系,数学与各种文化的联系等.数学文化是进行数学课程思政的天然资源库,教师不仅要讲好数学,更要弘扬数学文化,讲好数学故事.例如,圆的面积公式S=πr2,其中圆周率π是一个无理数,教师可以在教学中引入中国古代数学家刘徽的“割圆术”———当时计算圆周率的比较先进的算法,至今仍有一定的应用价值.它体现了以直代曲、无限趋近、“内外夹逼”的思想,这些思想是人们在解决数学问题时最基本、最朴素的思想.学生感受中国古代的先进文化,增强民族自豪感,激发学习数学科学知识的兴趣.数学文化视野也是多角度的,主要可以从以下几个方面进行思政融合,如科学精神,数学家们坚持不懈、勇于创新、实事求是的精神是值得我们学习的;爱国情怀,中国在古代数学史上取得的辉煌的成就,现在科技上正获得伟大的成就;职业精神或者工匠精神,学习数学需要一丝不苟、精益求精的态度正是未来职业所需要的.
总之,教育的根本目标是培养人,数学文化是很重要的课程思政来源,可以让学生在提高数学核心素养的同时,深刻感受数学家热烈的爱国情怀,严谨的科学态度,优秀的思想品德.
数学文化融入课堂,发挥其思政教育作用,离不开教师的作用.教师在数学课堂中起着主导作用,是课堂教学的设计者和实施者.因此,增强数学教师的思政素养,使其掌握正确的思想指引、价值塑造的方法,有助于数学课程思政的设计实施.教师要平时多关注社会热点事件,学习相关理论知识,提高自己的政治素养,做有理想信念、有道德情操、有扎实知识、有仁爱之心的“四有”老师.只有全体教师树立了正确的思想观念,才能把这种观念传递给每一名学生.教师要注重以身作则,言传身教,发挥示范引领的作用,在课堂上的工作态度,做事风格,课堂语言都是潜移默化的思政教育.数学教师如果粉笔板书工整漂亮,那学生的笔记也会跟着模仿;教师教学一丝不苟,精益求精,那么学生也会将这种精神传承,将来在工作中秉承工匠精神.因此,教师要提高自己的专业素养,在日常的教学中影响着学生,把好的品质习惯传递给学生.
【参考文献】
[1]汪晓勤.HPM:数学史与数学教育[M].北京:科学出版社,2017,5.
[2]朱聿铭.高等数学课程思政建设探索与实践[J].佳木斯职业学院学报,2022(11):100-102
[3]张倬华,数学文化融入三角函数单元教学的案例设计[D].河南科技学院,2022.

