锂电池SOC和SOH的自适应联合在线估算方法

俞志骏 安斯光 汪 伟

(中国计量大学机电工程学院 浙江 杭州 310018)

0 引 言

由于锂电池在电动汽车中的广泛应用,电池管理系统(Battery Management System,BMS)作为监控电池状态并为用户提供指导信息的关键部件,已成为电动汽车控制系统中必不可少的部分。荷电状态(SOC)和健康状态(SOH)是BMS中的两个基本指标[1],其中：SOC是剩余电池容量与可用电池容量之比,用来描述电池的荷电状态;SOH被定义为电池的老化程度,并为用户及时更换电池提供参考。SOC的估算是为BMS控制电池的充电和放电过程提供了数据支持,从而确保电池在每个充放电循环中都处于最佳工作状态[2]。SOH的估算是为了确保电池性能在设计的有效寿命内,可以根据SOH有效地调控电池充电方式,从而延长电池的剩余使用寿命[3]。由于系统硬件的限制,SOC和SOH的估算总是耗时较长,不能满足车辆运行时实时响应的需求。而且,估算精度随着电池的老化而降低。因此,开发一种准确快速地估算电池SOC和SOH的方法至关重要。

SOC和SOH都无法直接测量得到,其中SOC可以基于电池开路电压来计算得到,但是SOH估算比较复杂。在电池的SOH估算方法中,三项指标常用于估算SOH：充放电行为、容量和内部电阻[4]。(1) 充放电行为通常需要大量的电池充电和放电循环测试以及昂贵的实验设备[5],通常用于实验室研究。(2) 容量最常用于SOH预测[6-7],通过数据驱动算法,例如支持向量机[8]、神经网络[9]和深度学习[10]等。然而,数据驱动算法需要大量的计算资源,不适合在线估算。(3) 电池的内阻可以直接从等效电路模型获得,无须进行复杂的计算。通常通过基于等效电路模型的方法,运用无迹卡尔曼滤波器[11]和双卡尔曼滤波器[12]等预测算法跟踪电池状态。电池内阻与充放电行为密切相关,快速响应的充放电行为降低了寿命估算的准确性。为了跟踪SOH的动态变化,学者们将内阻作为SOH的指标[13],并给出了SOH的明确定义[14-15]。为了实现在线估算效果,本文将电池电阻作为电池SOH的指标。

在基于等效电路模型的算法中,模型参数的准确性直接影响SOC和SOH的估算。递归最小二乘(Recursive Least Squares,RLS)算法结构简单,稳定性高,最常用于系统参数识别[16]。但是,随着系统的迭代,前一个数据对后一个数据的影响将变得更大。为了减少旧数据对新数据的影响,学者们在RLS中添加了遗忘因子,构成了遗忘因子递归最小二乘算法(Forgetting Factor Recursive Least Square,FFRLS)。通过加强新数据,由新数据提供的信息量会逐渐削弱旧数据,防止数据饱和并迅速收敛到实际值[17]。然而,由于电池内部参数的快速变化特性,固定遗忘因子不足以满足快速收敛的需求。针对固定遗忘因子递归最小二乘法在在线识别中的不足,提出一种自适应遗忘因子策略,以提高模型参数识别的性能。

随着电池的老化,电池SOH可能会导致SOC的估算出现较大误差[18]。为了加强SOC与SOH之间的耦合,文献[14]中应用双重扩展卡尔曼滤波器(Dual Extended Kalman Filter,DEKF)来实现SOC和SOH的联合估计。Plett[19-20]最早提出了双重扩展卡尔曼滤波器以同时估算SOC和SOH,并使用电池容量和内阻同时作为SOH的指标。但是,随着双重估算框架的发展,研究人员发现电池SOH的变化特性通常比电池SOC的变化特性要慢得多,因此构造了多时间尺度扩展卡尔曼滤波器(Multi-time scale Extended Kalman Filter,MEKF),在较小的时间尺度上估算SOC,在较大的时间尺度上估算SOH,从而提高联合估算的计算效率[21],但是两个时间尺度的确定很大程度上取决于充电方式和标定校准。为了追踪在不同状态下锂电池内部发生的复杂动态,学者们提出了一种多尺度自适应参数识别方案,通过增加开路电压的估计精度,在不同的尺度上用DEKF来估计所有电池参数和SOC[22-23]。由于实际工作条件通常比实验室模拟要复杂得多,离线确定的固定时间尺度无法直接反映汽车在运行过程中的实际电池状态。因此,本文在固定时间尺度的基础上,根据在线测量得到的SOC来改变时间尺度,以进一步提高算法估算的准确性和效率。

1 自适应联合估算框架

1.1 SOH的定义

为了准确、快速地跟踪电池寿命,由于电池内阻与SOH之间存在很强的相关性,本文把电池内阻作为电池SOH的指标,参考[24]定义为：

(1)

式中：REOL为电池的实际最大容量降至标称容量的80%时的内阻,当实际最大容量下降到标称容量的80%时,该电池将被视为寿命终止;RBOL是电池出厂时的标称内阻,RNOW是电池当前内阻;本文定义的SOH范围是0%至100%。当SOH为0%时,意味着电池的实际最大容量已降至标称容量的80%,需要更换电池。根据传统的汽车寿命终止标准,设置REOL=2×RBOL,本文取RBOL=0.03 Ω。

1.2 SOC和SOH在线估算框架

我们在图1中提出一个可变时间尺度框架。首先,电池模型由自适应遗忘因子递归最小二乘(AFFRLS)方法确定。根据识别结果对遗忘因子进行自适应调整,以加快收敛速度,从而提高模型的准确性。为了平衡电池SOC和SOH之间的变化特性,分别在两个分离的时间尺度上执行参数识别和状态估算。在微观尺度上执行模型参数识别和SOC估算,而在宏观尺度上执行SOH估算。

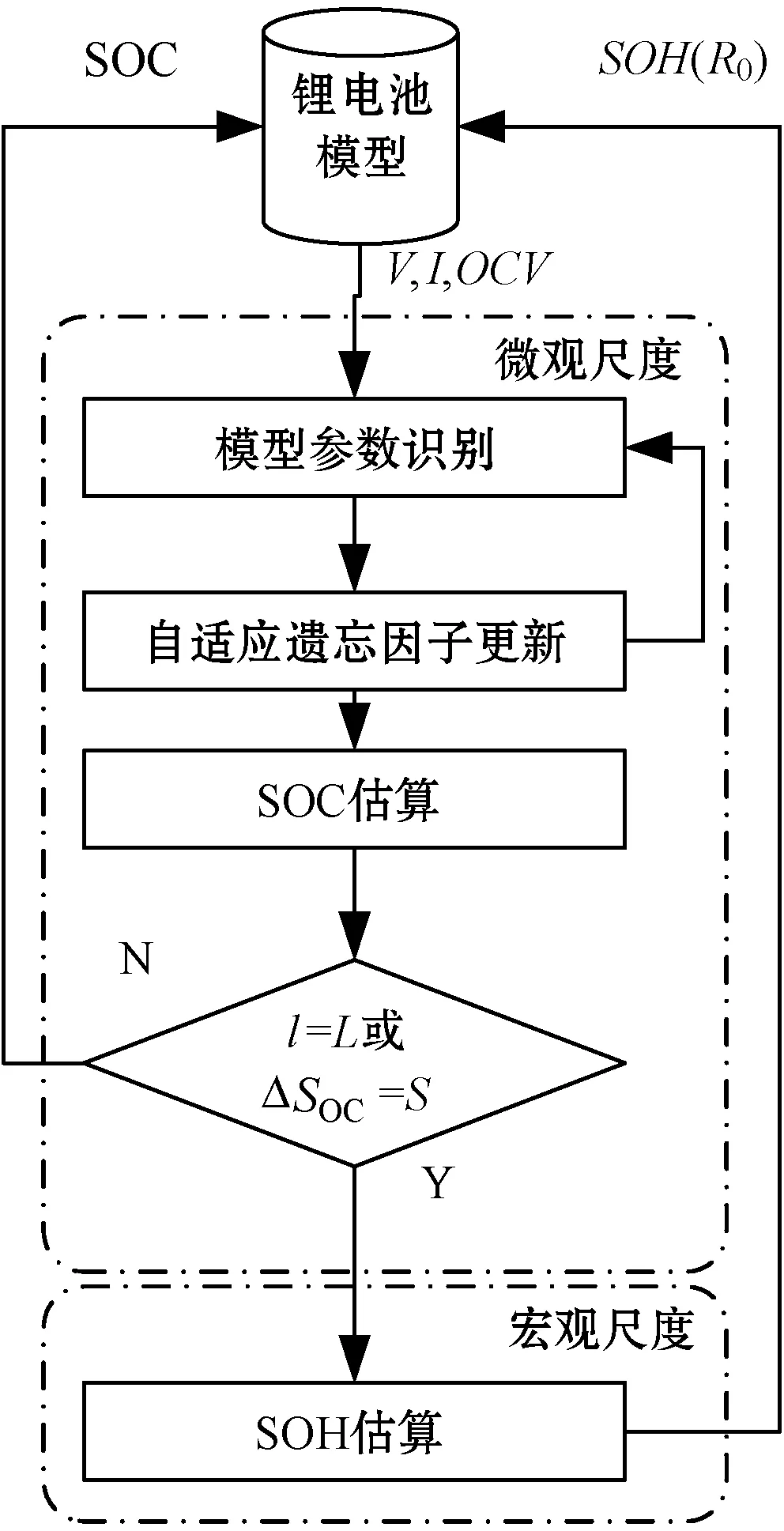
图1 SOC和SOH在线估算框架

分离时间尺度的算法的困难之一是确定时间尺度。有两种常用方法：(1) 使用固定的时间尺度,即在固定的时间范围内在微观尺度上执行算法,然后在宏观尺度上执行一次宏观算法,再返回微观尺度。(2) 使用变化的时间尺度,即默认在微观尺度上执行算法,当满足某些条件时,在宏观尺度上执行算法,如此循环。

两种算法各有优缺点。方法一通过离线测试确定时间尺度。该方法易于执行,但是在实际汽车行驶时会忽略电池的快速动态变化,因此无法反映真实的电池状态。方法二根据电池状态的变化来改变时间标度,以跟踪电池的动态响应。但是,真正的汽车并不总是保持高功率状态。在慢速动态下,此方法对电池状态的响应不佳。

为了减少离线数据对状态估算的影响,本文提出一种可变时间尺度扩展卡尔曼滤波器(VEKF)。VEKF结合了以上两种方法的优点,在固定的时间刻度上添加了时间尺度观测器。由于电池的SOC在电池运行时会发生明显变化,因此SOC被用作可变时间尺度的判断条件。具体方法是在离线确定的固定时间范围内,如果SOC变化量达到阈值,则改变时间尺度。

2 模型参数辨识

基于二阶RC模型和FFRLS方法,提出一种新型自适应遗忘因子策略。BMS在线测量的端电压和端电流视为电池模型的已知量,作为识别算法的输入,同时,遗忘因子根据当前周期和先前周期的输入之间的误差进行调整。基于自适应识别算法,算法更快的收敛速度可以实现在线更新电池内阻R0,以提高模型精度,并为下一次电池状态估算提供依据。

2.1 等效电路模型

二阶RC模型常用于锂电池的建模,与一阶RC模型相比,二阶RC模型更符合估算算法对模型高精度的要求,本文中不再赘述。如图2所示,其中：i为负载电流;u为端电压;R0为内阻;R1、C1和R2、C2代表电池单元扩散过程和电荷转移过程;u1和u2代表R1、C1和R2、C2分支电压,电压源Uoc用于描述与SOC直接相关的开路电压(Open Circuit Voltage,OCV)。

图2 二阶RC模型

根据基尔霍夫电压和电流定律,二阶RC模型的电气特性方程由表示为：

u(k)=Uoc[SOC(k)]-u1-u2-i(k)·R0

(2)

式中：Uoc[SOC(k)]表示根据OCV-SOC曲线拟合获得的开路电压。

2.2 自适应遗忘因子递归最小二乘法

电池等效电路模型的参数辨识通过自适应遗忘因子递归最小二乘法实现。采用递推最小二乘方法建立电池模型状态空间方程,参数辨识公式如下：

u(k)=θ1E(k-1)+θ2E(k-2)+θ3i(k)+

θ4i(k-1)+θ5i(k-2)

(3)

E(k)=Uoc(k)-u(k)

(4)

(5)

式中：T是采样时间。在FFRLS中,遗忘因子是固定的,很难适应在线参数识别的动态过程。当参数误差较大时,遗忘因子会增强新数据,导致无法尽快收敛以减小误差;当参数误差较小时,旧数据的大权重导致无法快速地跟踪动态响应。在电池模型辨识中,遗忘因子通常取值范围为0.95～1.00。较小的遗忘因子收敛速度较快,但在快速动态变化下辨识结果会失真;如果遗忘因子接近1,FFRLS退化为普通的RLS,具有较高的稳定性,但收敛速度较慢,无法快速跟踪实际值。因此,需要根据参数误差来自适应地改变遗忘因子,在电池参数快速变化的情况下实现更快的收敛速度和较小的识别误差。

基于以上分析,本文对FFRLS进行了改良。改进后的AFFRLS算法过程如下：

步骤1参数初始化,k=1,设定λmin、eN、E-1、E-2、θ0、P0初值。

步骤2数据输入矩阵：

(6)

计算增益K：

(7)

计算输出预测和误差：

(8)

ek=uk-Ek

(9)

更新估计参数θ(k)：

θk=θk-1+Kkek

(10)

更新协方差矩阵：

(11)

步骤3更新遗忘因子：

(12)

计算参数模型：R0、R1、C1、R2、C2

返回步骤2。

在每个算法周期中,BMS都会测量端电压u和端电流i。根据离线拟合得到的OCV-SOC曲线,可以获得模型开路电压OCV。基于模型Uoc以及测得的u和i,在执行AFFRLS之后,可以计算得到模型的R0、R1、C1、R2和C2等参数。

其中：λmin表示遗忘因子的最小值;eN表示允许的预期误差,两者均为固定值。当e(k)接近eN时,为了保持算法的稳定性,λ实现了普通FFRLS的功能;当e(k)接近0时,μ(k)接近1,λ(k)大约为1,此时,系统误差很小,而较大的遗忘因子可以有效地防止误差增加;当e(k)接近无穷大时,μ(k)接近无穷大,而λ(k)接近λmin。此时,系统误差较大,遗忘因子越小,收敛速度越快,误差快速减小。

3 基于可变时间尺度扩展卡尔曼滤波器的SOC和SOH联合估算

根据二阶RC等效电路模型,建立离散状态空间方程,以估算电池SOC和SOH。公式如下：

(13)

R0(k)=R0(k-1)+v(k-1)

(14)

式中：u1和u2代表R1、C1和R2、C2分支电压;i为负载电流;QN表示电池的当前最大容量,并且电池的最大容量会随着电池的老化而减小;η表示电池的充放电效率;w(k-1)和v(k-1)分别表示SOC和R0的观测误差。用两个离散状态空间方程式分别估算电池的SOC和SOH。

输出观测模型表示为：

y(k)=Uoc[SOC(k)]-u1(k)-

u2(k)-i(k)·R0(k)

(15)

为了实现SOC和SOH的联合在线估算对于锂电池,可变时间尺度扩展卡尔曼滤波器(VEKF)的构造如下。

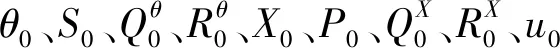
步骤2宏观尺度EKFθ赋值。

观测矩阵：

(16)

误差协方差矩阵：

(17)

步骤3宏观尺度EKFθ参数更新。

卡尔曼增益矩阵更新：

(18)

观测矩阵更新：

(19)

误差协方差矩阵更新：

(20)

循环l∈{1,2,…,L},计算：

步骤4微观尺度EKFX赋值。

观测矩阵：

(21)

误差协方差矩阵：

(22)

步骤5微观尺度EKFX参数更新。

卡尔曼增益矩阵更新：

(23)

观测矩阵更新：

(24)

误差协方差矩阵更新：

(25)

步骤6自适应时间尺度观察器。

If |SOCl-SOC1|≥0.3%

Break

(26)

其中：

θk=R0,k

(27)

Xk=[SOCku1,ku2,k]T

(28)

(29)

(30)

(31)

在每个算法周期中,在宏观尺度上执行EKFθ以实现电池内阻R0的动态更新,然后在微观尺度上执行AFFRLS以获得模型参数,并执行EKFX来实现SOC的估算。在每次迭代中,EKFX都会检查SOC变化是否超出阈值(本文中为0.3%),以确定是否需要执行SOH估算。

4 实验与结果分析

通过实验数据评估了自适应联合在线估算方法的性能。首先,基于二阶RC等效电路模型,通过动态应力测试(DST)条件循环数据演示并比较了FFRLS和AFFRLS的性能。最后,比较了电池SOC和SOH的三种估算算法,以评估本文提出的可变时间尺度下联合估算算法的性能。

4.1 实验数据

本文以美国DST工况为标准,应用马里兰大学CALCE电池研究小组的数据库[25],获得了电池的电压和电流循环数据。电池的初始容量为2.45 Ah,加速老化实验后的电池容量为2.38 Ah,SOH约为87%。老化电池在DST循环工况下的工作电压和电流数据如图3所示。图4中电池的OCV-SOC曲线通过离线拟合获得,其他参数通过在线识别获得。

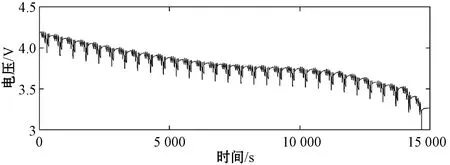
(a)

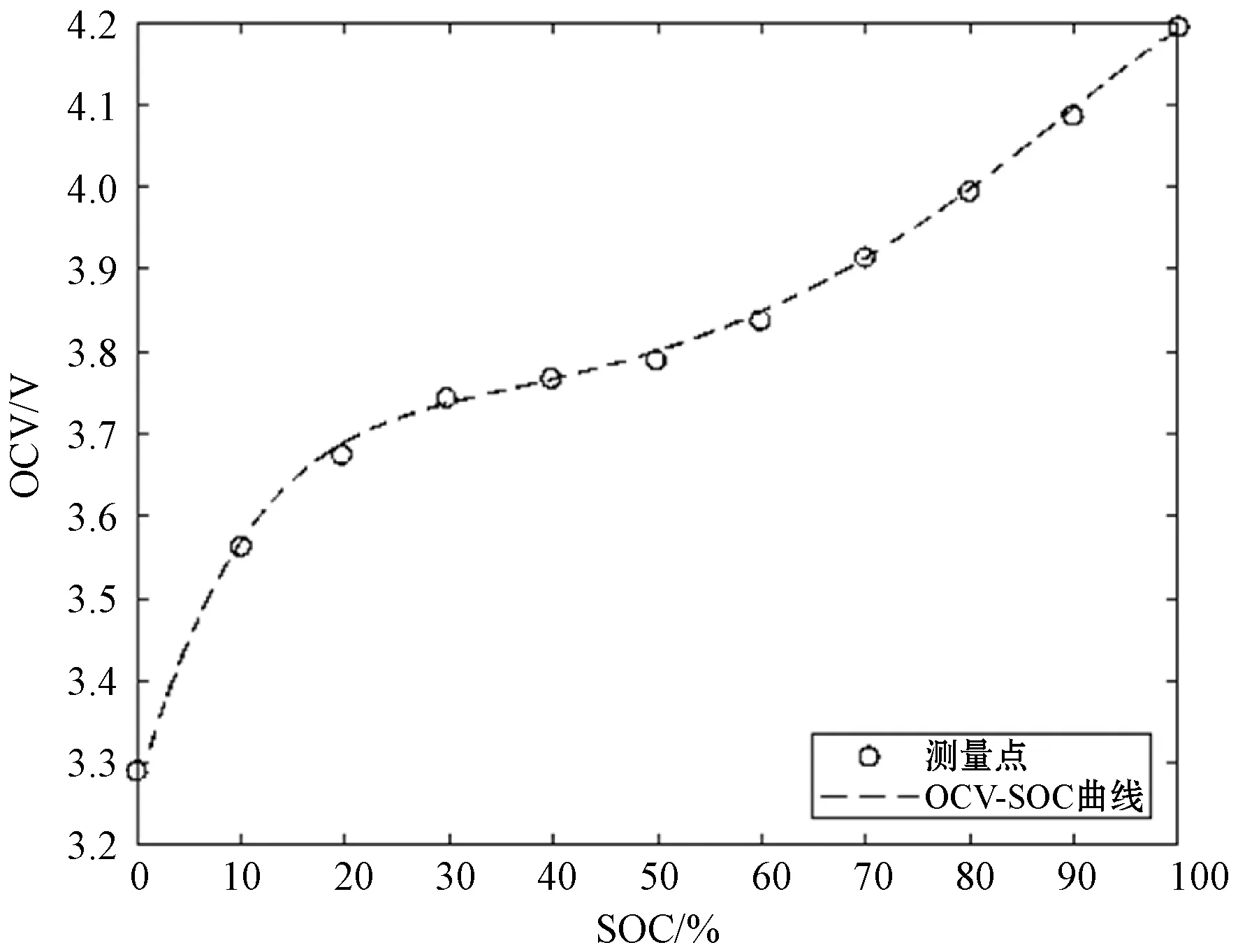
图4 OCV-SOC拟合曲线

4.2 AFFRLS和FFRLS在线参数识别精度分析

根据DST工况数据,分别用FFRLS和提出的AFFRLS识别模型参数。FFRLS中的遗忘因子设定为λ=0.99。考虑遗忘因子的取值范围,通过实验和验证,在AFFRLS算法中设置λmin=0.95,eN=0.05。

图5显示了相对误差分布的统计数据,将FFLSR和AFFRLF算法获得的端电压的相对误差分为十个区间,并记录每个区间内的点数。可以看出,在-0.5%到0.5%范围内,AFFRLF算法记录的点数比FFRLF方法要多,这意味着AFFRLF算法比原始FFRLF算法更有利于建立高精确的模型。

表1总结了两种算法的均方根误差(RMSE)。综合图5和表1可以看出,本文提出的AFFRLS算法识别的结果比原始FFRLS的结果更加精确。

表1

4.3 SOC与SOH的估算结果的分析

为了评估联合估算算法的性能,选择了两种常用算法：文献[21]中的FFRLS-MEKF和文献[14]中的AFFRLS-DEKF,并与本文算法进行了比较。表2总结了这项工作中使用的算法参数,为确保可比性,所有卡尔曼滤波器均使用相同的一组固定参数。

表2 卡尔曼滤波器的初始参数

根据三元锂电池的特性,确定离线的固定时间尺度L=60 s,并将时间尺度阈值设置为ΔSOC=0.3%。初始SOC设置为80%,通过设定错误的初始值,可以模拟现实情况下BMS在线获得数据后算法的精确度和鲁棒性。

图6和图7显示了SOC和SOH在DST工况下的估算结果。显然,与其他两种联合估算算法相比,本文提出的AFFRLS-VEKF联合算法估算的SOC和SOH估算与参考曲线基本一致,SOC估算误差小于0.3%,SOH估算误差小于1.1%。FFRLS-MEKF与AFFRLS-VEKF相比,自适应参数识别策略在微观尺度上提高了模型参数的识别精度,从而提高了SOC的估算精度,减小了在宏观尺度上SOC对SOH估算的影响。AFFRLS-DEKF和AFFRLS-VEKF相比,由于增加了可变时间尺度观测器,允许SOH的估算在宏观上保持相对稳定的值,从而提高了算法的鲁棒性。综上所述,本文提出的自适应联合估计算法在高度动态变化的复杂工况可以较快地跟踪到真实值,并维持较高的精确度,满足现实情况下对电池复杂充放电行为进行在线估计的要求。

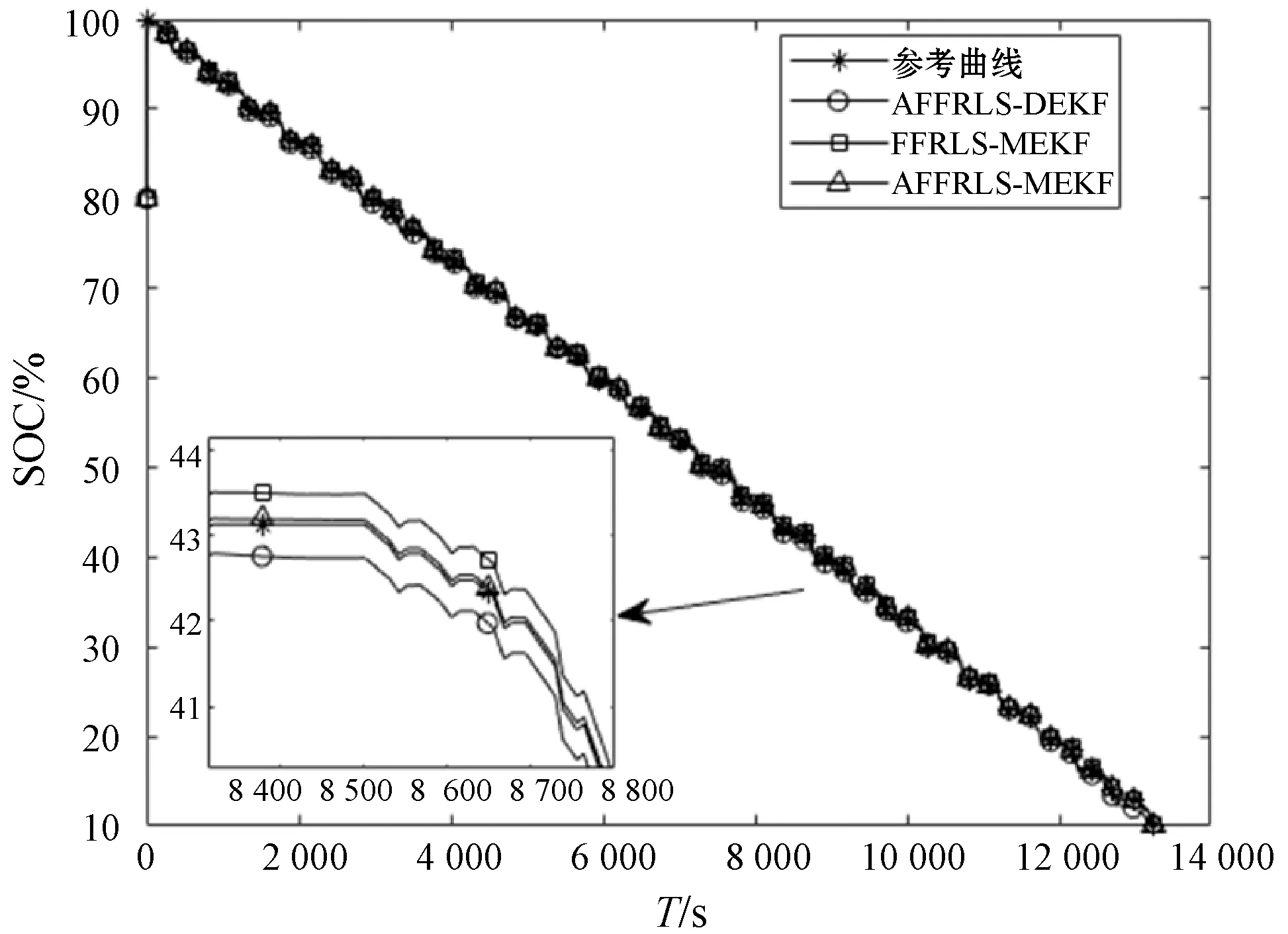
(a) SOC估计值

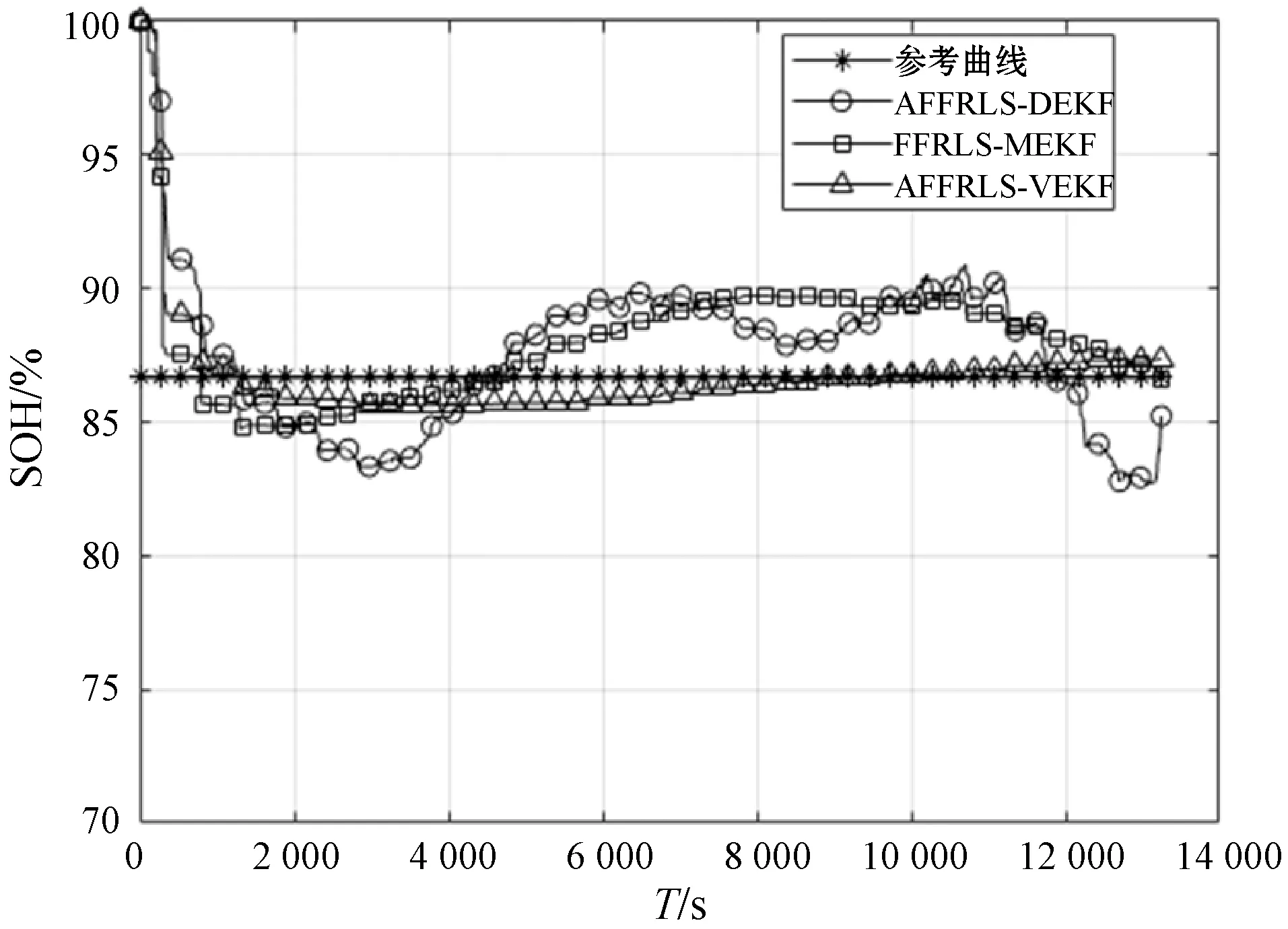
(a) SOH估计值

锂电池在线状态估算的仿真运行在配置有Intel i7-8700 CPU@3.20 GHz和16 GB RAM的Windows 10计算机上。以上三种算法均在MATLAB环境下运行。为了比较计算复杂度,每种算法执行了100次仿真并计算了平均执行时间。在DST工况下,如表3所示,AFFRLS-DEKF算法需要最长的计算时间,而FFRLS-MEKF需要最少的计算时间。本文的自适应联合估计算法运行15 000组数据点的平均计算时间为1.22 s,平均每组计算时间小于0.000 1 s,应用于BMS中可以实现电池状态在线估计。本文算法不仅提高了计算精度,而且提高了计算效率。这对减轻BMS硬件的计算负担并更好地进行电池状态的在线估算非常重要。

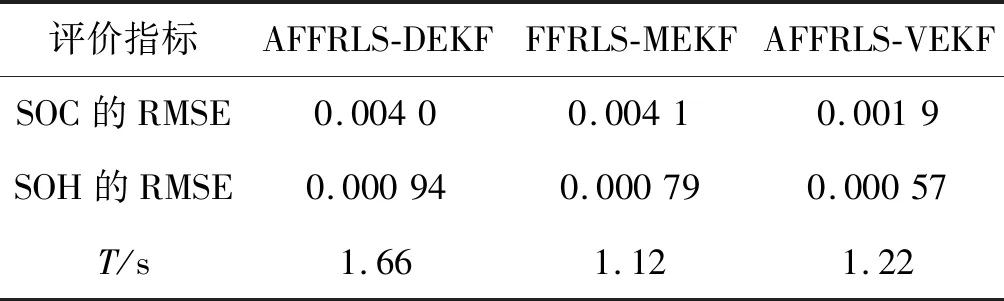
表3 SOC和SOH估算结果比较

5 结 语

本文提出一种基于遗忘因子最小二乘和可变时间尺度扩展卡尔曼滤波器的自适应联合估算算法,以在线估算锂电池SOC和SOH。与传统方法相比,本文方法可以在模型识别中获得更好的准确性,并且在状态估算中可以更快地匹配复杂的动态响应。基于DST工况数据的仿真验证了自适应联合估算算法的精确度和效率,SOC估算误差小于0.3%,SOH估算误差小于1.1%。下一步工作是设计电池充放电和均衡装置,将本文算法应用于BMS中,实现锂电池充放电状态下的电池状态实时在线估计。