考虑时空相关的交通事故热点道路识别方法

张忠贵 董 鑫 李成峰 程志远 王玉岚

1(湖北第二师范学院建筑与材料工程学院 湖北 武汉 430205)

2(湖北省BIM智慧建造国际科技合作基地 湖北 武汉 430205)

3(熊猫智慧水务有限公司 上海 201799)

0 引 言

随着我国城镇化进程加快,道路设施规模迅速扩大,车辆保有量增大,道路交通事故(以下简称交通事故)频发。与其他发达国家相比,中国的交通事故问题尤为严重,从万车事故死亡率来看,中国是9.93,远高于美国1.79、俄罗斯1.04、日本0.81的水平[1],严重影响了公众的生命财产安全。

道路交通系统是包括“人、车、路、环境”四大要素的一体化复杂系统。从交通设施管理部门角度,改造道路设施,提升道路通行条件,是降低交通事故的有效途径之一。但是面对海量的道路设施,在有限的经费和人力条件下,先改造哪些道路才能降低交通事故发生的频率,是交通管理部门面对的难题。

国内外学者在交通事故道路热点分析领域进行了一系列研究。戴永安[1]在城市化与交通事故发生之间关系分析的基础上,考察中国交通事故发生的空间相关性,并对影响交通事故次数和经济损失的因素进行了空间计量分析。陆化普等[2]以密度分析方法对深圳市道路交通事故多发的区域和事故严重程度较高的区域进行鉴别。蒋宏等[3]提出了基于空间自相关鉴别城市道路事故多发点的方法,并生成交通事故多发点分布图。王颖志等[4]提出一种基于交通事故场景的网络时空核密度估计值作为鉴别指标,用累计频率法和零膨胀的负二项回归模型确定鉴别阈值的事故多发点鉴别方法。Blazquez等[5]对智利圣地亚哥2000年-2008年期间儿童交通事故进行了时空分析,并采用核密度方法分析高密度的儿童交通事故聚类。Mitra[6]采用空间自相关和贝叶斯空间统计方法分析道路交叉口与交通事故的空间关系。Ouni等[7]基于道路安全风险指数,研究了空间自相关度量的性能稳定性。上述研究成果为本文的研究内容提供了坚实的基础。

但是,交通事故本质上作为一种道路现象,必须依附于交通网络。从交通设施管理部门的角度,上述研究多聚焦于交通事故的热点分析,较少考虑交通事故与道路网络的时空相关特征,不够直接,影响了交通事故道路热点分析方法的实用性。

针对上述问题,本文从交通设施管理部门角度出发,以道路网络而非交通事故为核心研究对象,考虑交通事故与道路网络的时空相关特征,提出线模式交通事故热点道路分析方法。本文方法可直接发现交通事故热点道路,从而为交通设施管理部门制定合理的改造计划提供支撑,降低交通事故发生的频率。

1 交通事故场景下时空相关的定义

从交通工程的角度,道路作为交通的载体,构成了复杂的交通网络,对交通事故的发生频率具有重要的影响。交通事故必然发生于某条道路上,本质上作为一种道路现象,与道路空间上密切相关,时间上趋于邻近,具有空间与时间聚集性。

此外,从地理信息科学的角度,时空相关可分为几何、拓扑、属性、时间相关。具体到交通事故领域,可分为几何相关、属性相关、时间相关。

综上所述,交通事故场景下时空相关可分为交通事故-道路几何相关、交通事故-道路属性相关、交通事故-交通事故时间相关。

定义1交通事故-道路几何相关。交通事故与-道路的最短距离小于半径参数ε时,交通事故与道路几何相关。

考虑到道路绘制精度与交通事故的全球卫星定位导航系统(GNSS)(如北斗系统、GPS系统)的定位精度,交通事故与道路通常并不是严格意义上的几何相交。因此,半径参数ε与研究区域内道路宽度、绘制精度、定位精度相关。

定义2交通事故-道路属性相关。交通事故的道路名称属性与道路的名称属性相匹配,交通事故与道路属性相关。

定义3交通事故-道路空间相关。将与交通事故几何相关的道路集合按照交通事故与路段的最短距离从小到大排列。该集合中第一条与交通事故属性相关的道路与交通事故空间相关。

特别地,由于交通事故位置或道路名称属性录入的不规范或缺失,当交通事故无属性相关的道路时,交通事故几何相关道路集合中与交通事故最邻近的路段为交通事故空间相关道路。

典型的交通事故-道路空间相关如图1所示。交通事故1与道路2、3几何相关,与道路2属性相关,与道路2空间相关。

图1 交通事故-道路空间相关

需要指出的是,由于存在定位精度和绘制精度的问题,与交通事故几何最邻近的道路不一定为空间相关道路。

定义4交通事故-交通事故时间相关。交通事故发生的时间距离小于时间窗口ΔT时,交通事故-交通事故时间相关。

2 方法设计

2.1 交通事故空间聚合算法

基于交通事故-道路空间相关的定义,将交通事故、道路空间数据作为输入,采用如图2所示的核心数据结构,空间聚合交通事故。算法数据结构包括交通事故(crash)、道路(road)、交通事故集合(crash_tbl)、道路集合(road_tbl)等核心空间对象。

图2 算法核心数据结构

交通事故空间聚合算法包括如下步骤,伪代码如图3所示。

图3 交通事故空间聚合算法

(1) 读取交通事故、道路空间数据的属性、几何、拓扑信息到交通事故表、道路表。

(2) 遍历交通事故表,当所有交通事故均访问时终止。

(3) 对于任意交通事故,进行交通事故空间聚合,构建交通事故缓冲区。考虑10车道道路(标准车道宽度3.7 m,道路中心线距离道路边线为18.5 m)及交通事故定位精度10 m,缓冲区半径ε取28.5 m。

(4) 交通事故-道路几何相关分析。空间查询道路空间数据中与交通事故缓冲区相交的道路,得到与交通事故几何相关道路集合,并按照交通事故与道路的最短距离从小到大排序。

(5) 交通事故-道路空间相关分析。求解几何相关道路集合中第一个与交通事故属性相关的道路,设置为交通事故空间相关道路。若无属性相关道路,将几何相关道路集合中第一条道路设置为与交通事故空间相关的道路。

(6) 若存在交通事故空间相关道路：交通事故的空间相关道路id赋值;道路的空间相关交通事故数目加一,添加到交通事故id列表。

(7) 将交通事故表、道路表写回交通事故、道路空间数据。

2.2 交通事故时空立方体

交通事故时空立方体采用二维坐标轴(x、y轴)来表示交通事故的平面位置,用一维的时间轴(z轴)表示平面位置上交通事故数量随时间的变化,从而构建一个由平面空间和时间轴组成的融合交通事故数量的时空立方体[8]。可运用时间维的几何特性来表达交通事故的空间分布随时间的变化过程。

交通事故时空立方体模型基于统一尺寸的平面位置网格,通过统计各时空条柱中包含的交通事故数目,将交通事故统计到统一尺寸时空条柱中。但是,交通事故空间分布于线状道路上。线状道路长度不同、形态各异,采用统一尺寸的平面位置网格来统计交通事故数目存在一定的偏差。因此,时空条柱高事故率不一定是交通事故热点。本文将通过线模式热点道路分析,得出交通事故热点道路。

2.3 线模式热点道路分析(Getis-Ord Gi*)

Getis-Ord G统计量[9]包括Getis-Ord General G和Getis-Ord Gi*,由Ord教授和Getis教授提出。Getis-Ord General G用于定性判定是否存在高值空间聚类或低值空间聚类。Getis-Ord Gi*用于定量计算研究区域中具有统计显著性的高值空间聚类和低值空间聚类。

Getis-Ord Gi*统计量是衡量局部空间自相关[10]特征的一种重要指标,广泛应用于交通事故分析、犯罪热点分析[11]等领域。本文采用Getis-Ord Gi*方法,逐一计算每条道路的Getis-Ord Gi*统计量,从微观上识别具有统计显著性的交通事故数目高值道路聚类(即交通事故热点道路)。

根据地理学第一定律,地理事物或属性在空间分布上互为相关,包括集聚或随机或规则的空间分布模式。现实中,交通事故具有空间集聚性。从统计学的角度,为了证明交通事故具有空间集聚性,我们需设定“交通事故在研究区域中是随机分布”的零假设,并期望检验结果推翻该零假设。空间分布模式的检验,采用计算标准化的Getis-Ord Gi*统计量的Z得分(Gi*ZScore)和置信度-P值(Gi*PValue)来实现。

Gi*ZScore计算方法如式(1)所示[9,12]。

(1)

对于线模式空间热点道路分析：xj是道路j相关的交通事故数目,采用交通事故空间聚合算法计算。wij是道路i和道路j之间的空间权重。当道路i和道路j的距离小于距离阈值distanceband且空间权重Wij为道路之间的反距离(1/lij);否则为0,如式(2)所示。

(2)

(3)

Gi*ZScore为道路i的Getis-Ord Gi*统计量Z得分。对于具有显著统计学意义的Gi*ZScore正数,Gi*ZScore越高,交通事故数目高值道路聚类越紧密,可判定为具有统计学意义的交通事故热点道路。

3 方法验证

3.1 实验数据

本节以某城市机动车道路与交通事故(非交叉口事故)为例,验证交通事故热点道路识别方法。

OSM格式的道路空间数据可从Geofabrik’s free server下载,格式为ArcGIS Shapefile。道路空间数据包括道路名称、等级、编码等信息。交通事故数据采用ArcGIS Shapefile格式存储,包含编号、地理坐标、所在道路、事故等级、发生时间、处理时间等信息。

857个交通事故空间覆盖城市757条机动车道路(如图4所示),时间跨度从2008年到2018年。

3.2 交通事故空间聚合结果

对于实验数据,采用“2交通事故空间聚合算法”的方法,计算道路的、,交通事故的属性值,建立交通事故-道路空间关系。其中,道路的属性作为核心输入参数之一,参与热点分析。

以78号道路为例,对于表达交通事故-道路空间相关的属性进行地图可视化,得到如图5所示的交通事故空间聚合结果。78号道路空间相关的交通事故列表为649、62、260、659号交通事故,其交通事故数目为4。

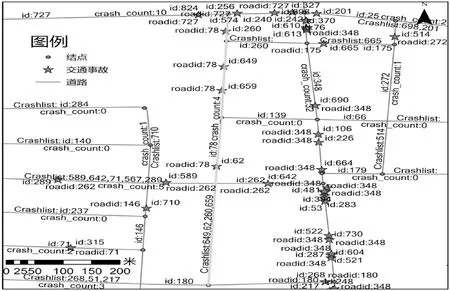
图5 交通事故空间聚合结果可视化

3.3 交通事故时空立方体分析

基于定义4,采用1个月为时间窗口[13],交通事故发生的时间距离小于1个月时,交通事故时间相关。对于从2008年到2018年实验数据,时空立方体时间上将857个交通事故聚合到126个时间步长间隔内;空间上将857个交通事故聚合到8 300个86 m×86 m方形格网中。在8 300个方形格网中,452个格网对于至少一个时间步长间隔包含至少一个交通事故。因此,具有统计意义的交通事故时空立方体由56 952个时空条柱组成。交通事故计数随时间推移具有统计显著性的减少,如图6所示。

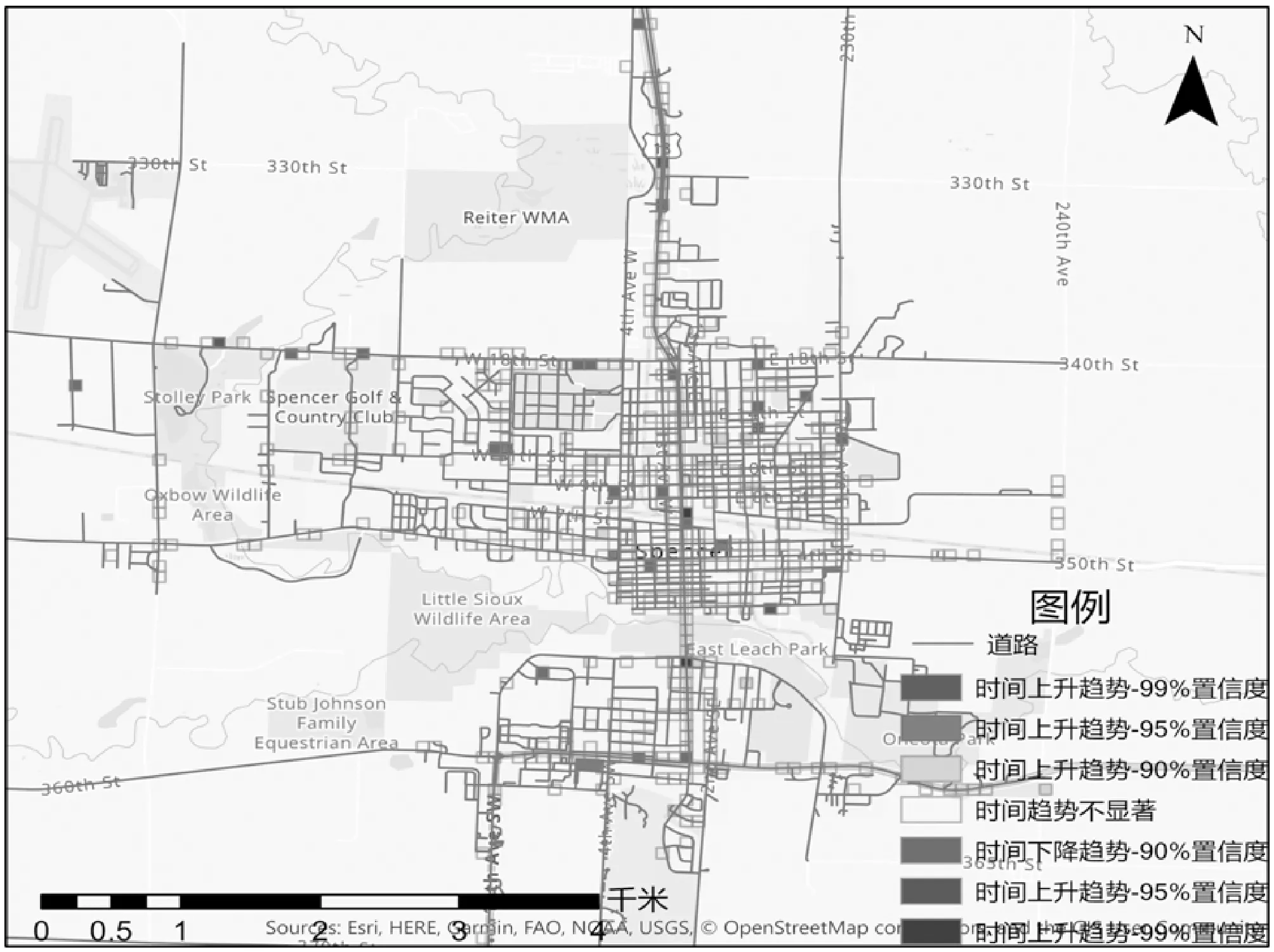
图6 交通事故时空立方体分析可视化

3.4 交通事故热点道路分析

交通事故时空立方体分析未考虑交通事故空间分布于线状道路上的空间分布特征,存在一定的偏差。本节以道路而非交通事故为核心研究对象,将道路的属性作为核心输入参数,并排除孤立的道路,计算每条道路的Getis-Ord Gi*统计量的Z得分Gi*ZScore、P值Gi*PValue。受限于篇幅,以交通事故数从大到小排列,列出前30条道路的热点分析计算结果如表1所示。

表1 热点分析计算结果

一般地,我们认为置信度超过90%时,具有显著的统计学意义。根据第三节的描述,我们设定“交通事故在研究区域中是随机分布”的零假设：当Gi*PValue小于0.10且Gi*ZScore大于1.65时,道路i的交通事故数目的空间分布模式为随机分布的概率小于10%,道路i的交通事故数目的空间分布模式为集聚(正相关,热点)的置信度大于90%;当Gi*PValue小于0.10且Gi*ZScore小于-1.65时,道路i的交通事故数目的空间分布模式为随机分布的概率小于10%,道路i的交通事故数目的空间分布模式为规则(负相关)的置信度大于90%。同理,可得出95%、99%的置信度的空间分布模式。

在实验区域内757条道路中,根据空间分布模式检验规则,可得出：事故数大于等于12的16条道路为99%置信度的热点道路;事故数在9～11间的7条道路为95%置信度的热点道路;事故数在8～9间的3条道路为90%置信度的热点道路。其他道路为不具有统计显著性的非热点道路。

对实验区域内于99%、95%、90%置信度的交通事故热点道路分别以不同线型标注。由于地图篇幅有限,下图中部分贴近的道路实际为双向道路。热点分析的地图可视化结果如图7所示。

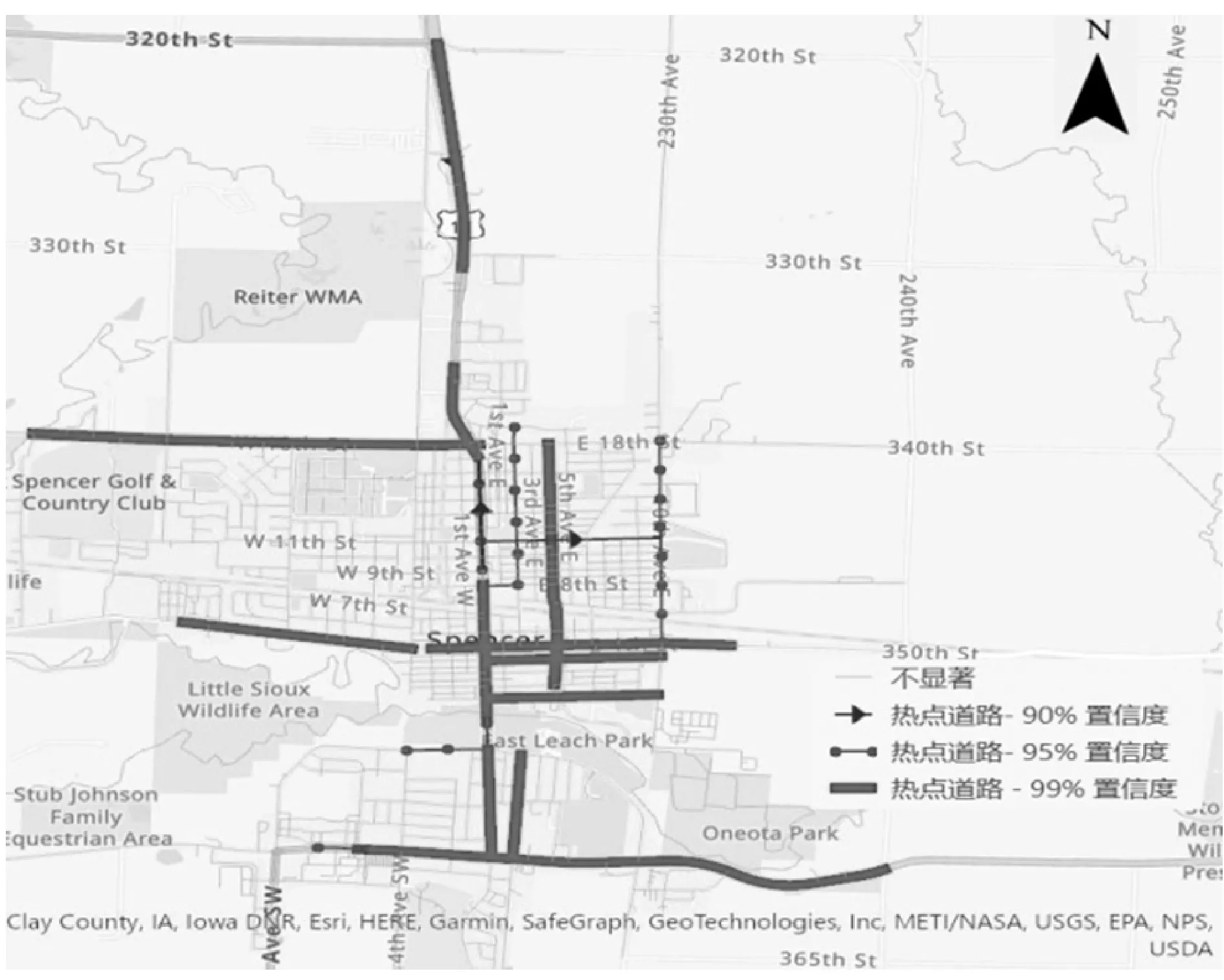
图7 空间相关热点道路的地图可视化

对于交通设施管理部门,优先改造上述空间相关热点道路设施,提升道路通行条件,是降低交通事故的有效途径之一。

3.5 与传统方法对比

对于该城市的交通事故按照所在道路进行计数统计,可知其多发生于US 18/N GRAND AVE、US 18/HIGHWAY BLVD、US 18/S GRAND AVE、W 4TH ST、US 71/11TH ST SW等道路。限于篇幅,以交通事故数从大到小排列,表2列出了前10条基于所在道路的交通事故计数统计表。

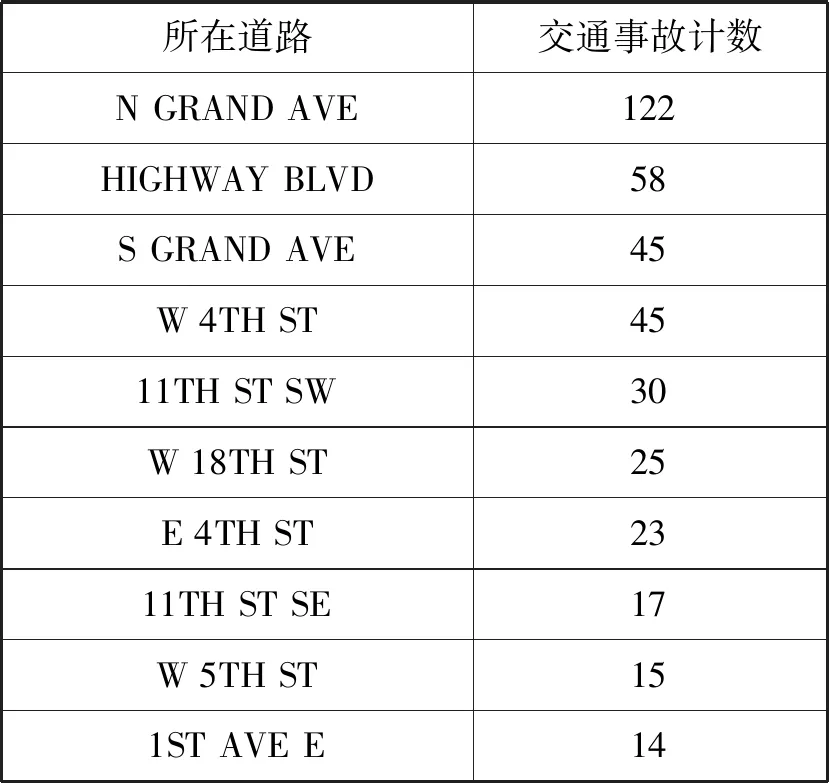
表2 交通事故计数统计表

上述道路可记为属性统计热点道路。

以表2为参照,验证表1的交通事故热点道路识别结果,可得到表3。需要指出的是,表1和表2中道路名称由两个不同部门录入,并不完全匹配,本文采用空间匹配及字符串模糊匹配的方法进行对应,如W 4TH ST与West 4th Street为同一名称道路。

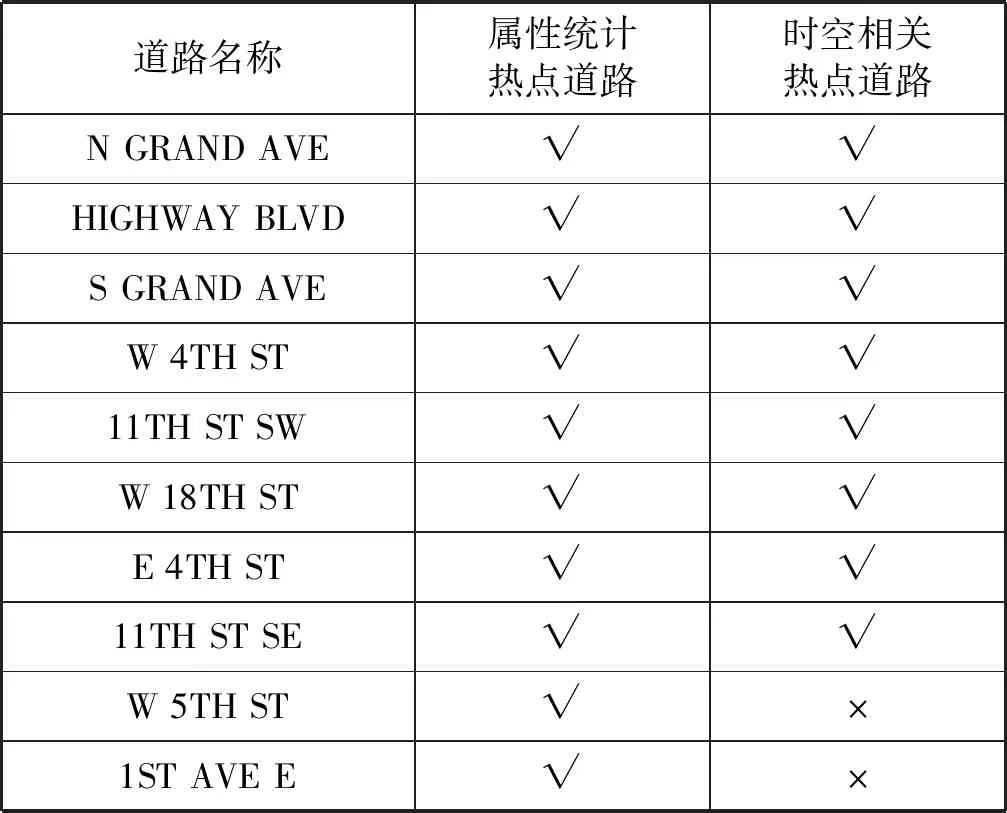
表3 属性统计与时空相关热点道路对比

从表3可知：(1) 交通事故热点道路与交通事故数目属性统计的热点道路80%吻合。(2) W 5TH ST(West 5th Street)、1ST AVE E(1st Avenue East)两条道路为属性统计热点道路。但是,在考虑了交通事故-道路时空相关性时,上述道路非时空相关热点道路。现实中,同名道路可能空间上并不连续,空间上距离较远,仅仅从道路名称上统计热点道路并不准确。以1ST AVE E道路为例,如图8所示,1ST AVE E 全长2 762.80 m,空间上断开,并分成多个路段,交通事故并非聚集在1ST AVE E道路上,因此非交通事故热点道路。

通过上述验证,相对于交通事故数目属性统计方法,本文提出的交通事故热点道路识别方法,可适应长距离同名道路和非连续同名道路的实际情况,计算出的交通事故热点道路更加精细及准确。

4 结 语

道路设施作为交通的载体,对交通事故的发生频率具有重要的影响。交通设施管理部门可利用时空相关交通事故热点道路识别方法,定位交通事故高发道路并开展交通安全决策,以减少交通事故。考虑时空相关的交通事故热点道路识别方法具有以下特点：

(1) 以道路而非交通事故为核心研究对象,将点状分布的交通事故通过空间聚合关联到道路的属性“交通事故数”,使研究成果更有针对性。

(2) 综合考虑交通事故-道路时空相关及交通事故空间自相关特征,可适应长距离同名道路和非连续同名道路的实际情况,计算出的交通事故热点道路更加精细及准确。

考虑时空相关的交通事故热点道路识别方法充分利用了交通事故-道路时空相关及交通事故空间自相关特征,可应用于道路交通安全评价,但也存在诸如交通事故时空聚合时间窗口确定、网络约束的道路时空距离计算等问题需要在后续研究中重点解决。