基于密度分区的出租车载客热点区域聚类分析

任丹萍 刘 琳 陈湘国

(河北工程大学信息与电气工程学院 河北 邯郸 056038)

(河北省安防信息感知与处理重点实验室 河北 邯郸 056038)

0 引 言

近年来,由于国家政策对城市化发展的大力扶持,城市人口急剧增长,城市居民收入增加、生活水平改善,出租车逐渐成为城市居民出行的重要选择方式[1]。同时随着车载GPS的普及[2],交通轨迹大数据愈发受到重视,出租车GPS轨迹数据作为其中一项重要组成部分,成为该领域研究热点[3]。

通过对出租车轨迹数据内在规律的挖掘,可以得到城市人口活动特征。例如在城市人口活动的时空规律分析方面,张俊涛等[4]提出将高斯定律引入出租车轨迹挖掘,通过轨迹的方向和数量特征,基于不同时间段对出租车轨迹数据进行挖掘。当然,城市居民的活动并非一成不变,在城市居民出行特征差异性方面[5],郑晓琳等[6]根据出租车轨迹数据中的时空分布差异、行程距离差异、空间社团结构差异三个方面,反映出城市人口活动模式的差异性,从而提升该研究在城市道路规划等领域的应用。出租车轨迹数据对城市人口活动规律的分析也不局限于日常活动,对于特殊的出行场景,例如旅游[7]、购物[8]等行为亦可以进行规律的挖掘。

基于不同应用场景,采用不同研究方法。结合出租车GPS轨迹数据的特点,选取聚类算法对热点区域进行挖掘,会达到更好的热点区域分布效果[9]。基于密度的聚类算法更适用于移动轨迹数据的聚类,对轨迹数据进行划分,例如DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法[10]可以从随机分布的出租车轨迹数据中发现聚类簇。在出租车载客热点区域的分析过程中,刘盼盼[11]提出了一种带有范围控制的算法,可以对空间数据快速聚类,实现出租车轨迹数据的细聚类;王贝贝[12]则是从时间的角度结合聚类算法对热点区域进行挖掘。但是由于该聚类算法采用的全局参数会导致聚类结果的精确度不高[13],所以,Kumar等[14]便对DBSCAN的聚类结果进行二次加工,使用最近原型规则将其扩展至数据集的其余部分。蔡莉等[15]则是从时空特征的角度,融合了位置数据,该模型基于数据层面,解决了轨迹数据分布不均匀的问题。

在针对出租车轨迹数据的研究中,挖掘的载客热点区域精确度不高,本文根据出租车GPS轨迹数据分布不均匀的特点,提出一种基于密度分区的聚类算法,对出租车轨迹数据进行聚类分析,得到城市人口活动热点区域。

1 数据预处理

1.1 数据描述

出租车轨迹数据集源于成都市1.4万多辆出租车的实际行驶轨迹,平均每天会产生5 000多万条出租车GPS轨迹数据。基于研究硬件环境的限制,选取成都市一周内的出租车GPS原始轨迹数据集,即以2014年8月18日至2014年8月24日的轨迹数据为例,作为实验数据。该数据集包含五个属性,具体如表1所示。

表1 出租车GPS轨迹数据属性

1.2 数据处理环境

基于出租车轨迹数据量较大,为提高轨迹数据处理速度,结合Spark部署模式的特点和硬件条件的限制,搭建Spark平台的local模式作为数据预处理的计算环境。具体过程为下载ApacheSpark并解压tra包,上传至集群的每个节点,设置PySpark模式的环境变量,从而可以在该模式下进行基于Python的数据预处理工作。

1.3 数据清洗

目前出租车原始轨迹数据采集过程中,主要依靠车载GPS传感器进行数据采集与传输,但由于各种外部或内部因素的影响,例如传感器故障、GPS信号较差、人为干预等,会导致GPS信号断传、重传,原始数据源缺失、重复或者存在异常值等。针对出租车轨迹数据中的“噪声”数据进行数据清洗,是数据预处理的第一步,也是获取准确的轨迹数据集的必要步骤。针对原始轨迹数据存在的问题,具体清洗过程如下：

(1) 去空。出租车GPS原始轨迹数据中包含部分缺失字段,影响数据分析的准确度。通过Python编程,筛选并删除缺失字段及字段所在的数据行,从而实现了数据集的完整性。

(2) 排序。出租车GPS原始轨迹数据呈无序排列。通过将出租车轨迹数据先以出租车序号升序排列,再以当前时刻升序排列,可以得到一天内有序的轨迹数据,达到了轨迹数据集的有序性的目的。

(3) 降重。出租车GPS原始轨迹数据含有重复数据。将出租车序号和当前时刻两个字段属性共同作为去除重复数据的评判标准,实现出租车轨迹数据的正确降重。

1.4 载客点提取

出租车轨迹数据的车载状态发生变化的具体表现为,当数值从“0”变为“1”时,表示当前时刻出租车的车载状态从空载变为载客,说明此时有乘客上车,其值为“1”对应的经纬度位置为出租车载客上车点位置。数值从“1”变为“0”,表示当前时刻出租车的车载状态从载客变为空载,说明此时有乘客下车,其值为“0”对应的经纬度位置则为下车点位置。

具体地,通过Python编程将每行数据的车载状态减去上一行数据的车载状态,通过其差值判断此时刻出租车的车载状态。若计算差值结果为“1”,表示该过程为乘客上车过程,选取车载状态为“1”的数据行为上车点。若计算差值结果为“-1”,表示该过程为乘客下车过程,选取车载状态为“0”的数据行为下车点,从而得到出租车载客点数据集。

1.5 数据筛选

出租车一次有效载客行驶时长是取决于乘客的实际出行需求,因此基于出租车上下车载客点数据集,计算乘客下车对应时刻与上车对应时刻之间的时间差值,得到一次有效载客行驶时长。出租车载客时长的变化趋势如图1所示。

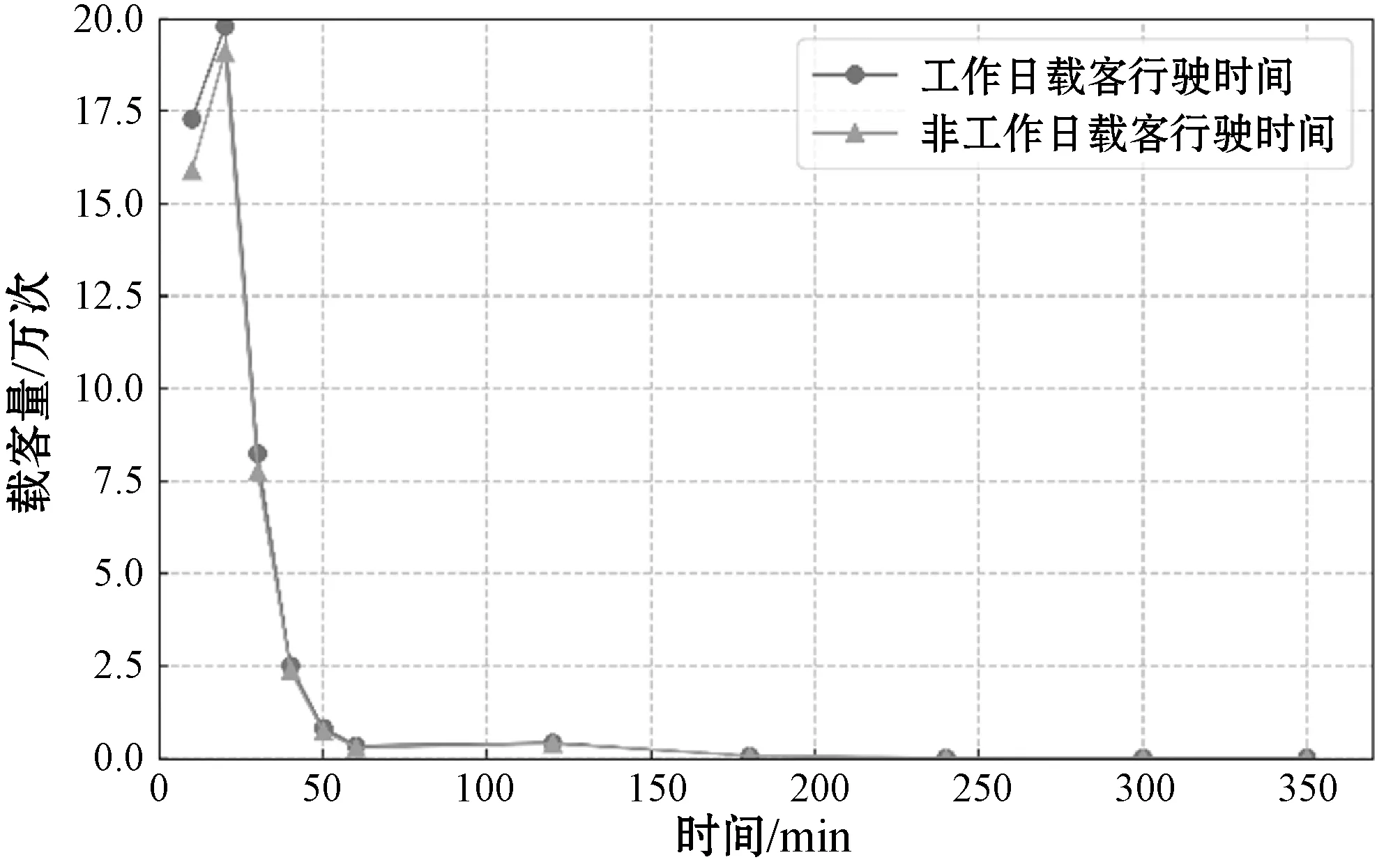
图1 出租车载客行驶时长

由图1分析可知,出租车载客行驶时长的高峰集中于10至20 min内。随着出租车载客行驶时长增加,载客量逐渐减少,变化曲线呈现出先增后减的规律。结合实际,选取载客行驶时长在2 min至2 h以内的轨迹数据。同时限定出租车载客行驶范围,取东经103°95′～104°18′和北纬30°54′～30°733′为研究区域。

1.6 坐标转换

为保证信息安全,不同地图采用不同的坐标系,因此轨迹数据匹配地图时需要进行坐标转换[16],即轨迹数据在同一地球的映射下,通过坐标的加密和解密,进行不同坐标系统间的相互转换。本文应用的坐标系种类如表2所示。

表2 坐标系说明

2 出租车载客行为时空分析

2.1 载客时间特征分析

城市居民的基本出行规律具有周期性,并且考虑到一天的出租车载客量存在偶然性,所以计算一周内工作日和非工作日的出租车平均载客量作为出租车载客高峰时段的分析数据,得到工作日和非工作日不同时段内出租车载客量随时间的变化规律如图2所示。

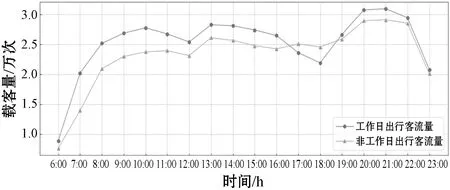
图2 出租车载客高峰分析

由图2分析可知,工作日和非工作日出租车载客量曲线变化趋势总体相似。根据高峰期特征,即在某时间段内出租车载客量明显增多且高于相邻时段内出租车的载客量可知,工作日出租车每时段平均载客量共出现三个高峰期,分别为早高峰(9：00-11：00)、午高峰(13：00-15：00)和晚高峰(20：00-22：00),符合成都居民“早九晚十”的生活节奏。非工作日载客高峰期则分为午高峰(13：00-15：00)和晚高峰(20：00-22：00)。

此外,通过载客时长,应用数学统计方法计算载客时长分布数,得到工作日和非工作日不同时间间隔内出租车的载客量变化如图3所示。

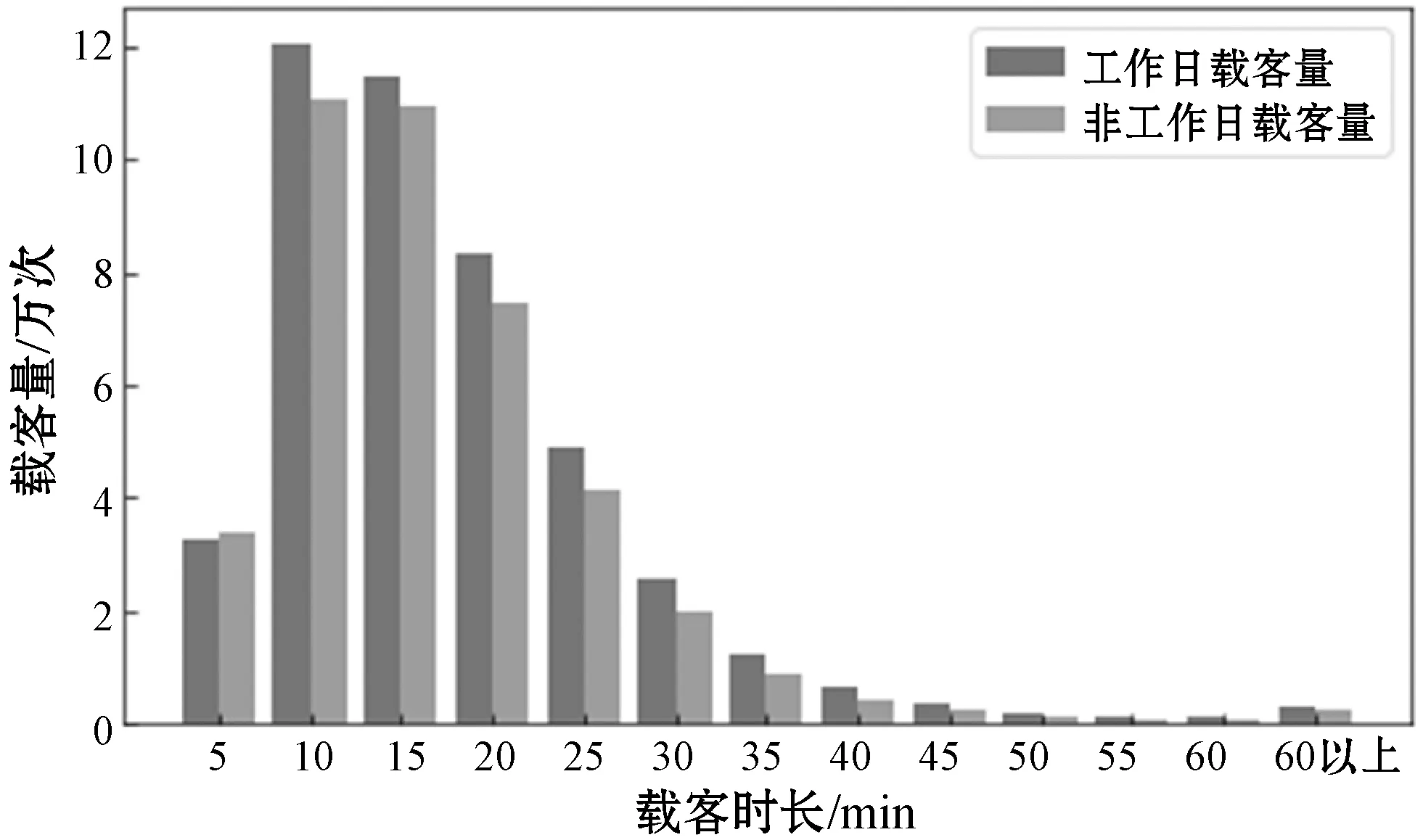
图3 出租车载客时长分布数

由图3分析可知,在工作日和非工作日期间,出租车载客时长数的变化趋势基本一致,随着载客时长的增加,载客次数增长,至载客时长为5至15 min内,载客次数达到高峰;超过30 min的时段内,出租车载客量仅占全部的5%左右。由此可知,出租车载客时长大部分集中在30 min以内,选择出租车出行更多的是短途出行。

2.2 载客空间特征分析

出租车载客空间,即出租车载客的上车点位置空间分布。结合出租车载客的时序特征,通过核密度分析不同时间段内出租车载客空间分布规律如图4所示。

图4 每时段载客空间分布

由图4分析可知,每时段的出租车载客空间分布不尽相同,比如在非高峰期时段内,出租车的载客区域分布较为平均;临近载客高峰时段,载客的热点区域分布逐渐凸显。而在早高峰、午高峰和晚高峰期间,载客空间的分布层次最为分明,热点区域分布集中。

因此,根据出租车载客的空间分布随时间的变化呈现出的递增和递减规律,分析其载客空间分布图,具体结果如表3所示。

表3 出租车载客区域统计表

3 出租车载客热点区域挖掘

3.1 算法思想

基于密度分区的DBSCAN聚类算法主要是通过求取每个出租车上车点位置数据的局部密度,得到密度峰值点作为簇中心。计算剩余轨迹点与密度峰值点间的欧氏距离,将其归入到距离最小的峰值点邻域内,实现对轨迹数据集基于密度的快速划分,得到不同密度的轨迹数据集。计算不同轨迹数据集对应的参数Eps和MinPts,实现基于密度分区的局部DBSCAN聚类,最后输出合并聚类结果。

3.2 算法步骤

基于密度分区的DBSCAN算法的相关定义如下：

定义1(局部密度) 对于给定的数据集D,其内对象i的局部密度如下：

(1)

对于χ(x)函数定义为：

(2)

式中：dij表示对象i与j之间的欧氏距离;dc表示截断距离,且由于该参数对实验结果影响较小,因此该参数的取值为使得数据集D内的每个对象的相邻平均对象数约为数据集内数据总数的2%[17]。

定义2(高局部密度点间的距离) 对于数据集D中的任意对象i,与局部更高密度点间的距离定义为：

(3)

其中,存在一种极端情况,即对象i本身的局部密度到达最高时,则该点的δi值定义为：

(4)

定义3(决策值) 对于数据集D中的任意对象i,结合该点的局部密度ρi和高局部密度距离δi得到其决策值,定义如下：

γi=ρi×δi

(5)

基于上述算法定义的阐述,基于密度分区的DBSCAN算法具体步骤如下：

步骤1输入出租车上车点位置数据集D,计算任意上车位置间的距离矩阵。

步骤2根据距离矩阵和截断距离dc,计算每个上车位置的局部密度ρi。

步骤3计算与高密度上车位置点的最小距离δi。

步骤4计算决策值γi,判断决策值差值是否大于其均值,若是,则标记为簇中心。

步骤5将剩余上车位置数据点按其局部密度降序排列,依次判断并划分到距离自己最近的簇中心,生成不同密度的上车点位置数据集Di。

步骤6计算不同密度上车点密度数据集Di对应的参数Epsi和MinPtsi。

步骤7将上车点密度数据集内的所有数据点均标记为未访问状态,任选一个未访问的上车点,判断该上车点以Epsi为半径的邻域内是否包含MinPtsi个上车点。若是,标记为核心点,建立新簇C,将邻域内所有的上车点加入簇C;否则,标记为噪声点。

步骤8将簇C中尚未访问的上车点依次计算其邻域内是否包含至少MinPtsi个上车点。若是,则将邻域内未归入任何一个簇的上车点加入到簇C中。

步骤9重复步骤8,继续检查C中未访问的上车点,直至没有新的上车点加入簇C为止。

步骤10重复步骤7-步骤9,直到所有上车点都加入某个簇或者标记为噪声点。合并不同密度上车点位置数据集Di的聚类结果,输出。

3.3 参数确定

本文利用出租车轨迹数据集自身的空间特性,自适应地求取参数值[18]。

(1) 确定Eps参数候选列表。参数Eps的选取,通过计算输入的出租车上车点位置数据集D中每个元素间的欧氏距离,得到其距离分布矩阵DISTn×n如下：

DISTn×n={dist(i,j)|1≤i≤n,1≤j≤n}

(6)

式中：n表示数据集D中对象数量;DISTn×n矩阵内的每一个元素为数据集D中的对象i和对象j间的欧氏距离。

将距离分布矩阵DISTn×n内的每一行元素按照升序进行排列,则第K列(K=1,2,…,n)的元素即为数据集D内所有对象的K-最近邻距离向量,表示为DISTn×k。对DISTn×k内的元素求数学期望,得到K-最近邻的平均距离作为参数Eps的候选参数列表,如图5所示。

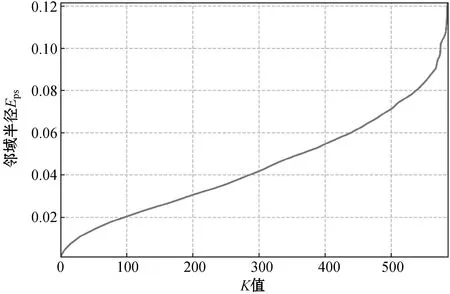
图5 Eps参数候选列表和K值关系

(2) 确定MinPts参数列表。参数MinPts的选取,在参数Eps的基础上,求出每个Eps对应的邻域内包含的对象数,采用数学期望法计算所有对象数的均值,即为数据集D的邻域密度阈值MinPts的值,计算公式如下：

(7)

式中：n为数据集D中的对象总数;Pi为对象i在以Eps为半径的邻域内包含的对象数量。MinPts参数候选列表与K值的关系曲线如图6所示。

图6 MinPts参数候选列表和K值关系

(3) 确定最优参数。根据上述内容确定的参数列表,依次选取K列元素对应的Eps值和MinPts值作为输入进行DBSCAN算法聚类,可以得到不同K值对应的最终聚类结果和生成的簇数。当同一个簇数连续出现三次及以上次数时,聚类结果趋于稳定,直至簇数再发生变化前,选取最后的K值最为最优K值,此时最优K值对应的Eps和MinPts的值作为最优参数。通过该计算方法得到的聚类簇数与K值之间的关系如图7所示。

图7 聚类簇数和K值关系

可以看出,当簇数为6时聚类结果趋于稳定,直至簇数再次发生变化前取得最优K值,此时K=12,结合图5、图6可知,对应的最优Eps=0.006 593 03,MinPts=18。

3.4 结果分析

选用的出租车实际上车点位置数据集含有7 824个数据,对其进行不同聚类分析,聚类参数的选取和聚类结果如表4所示,具体聚类结果如图8所示。

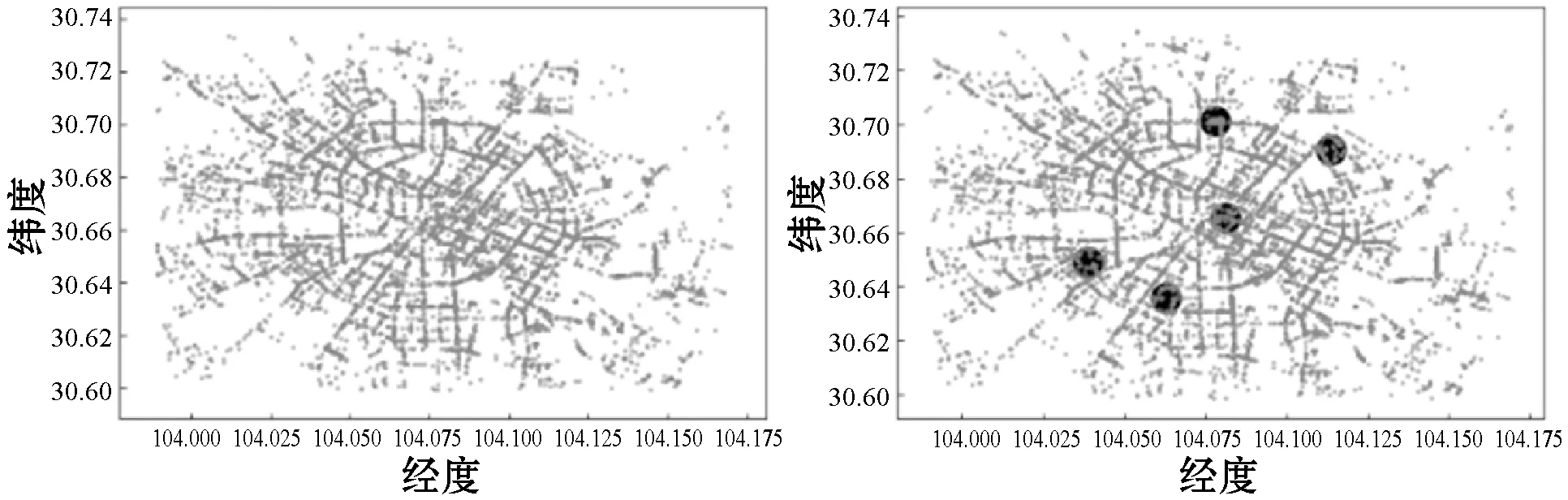
(a) 原始数据 (b) DBSCAN算法

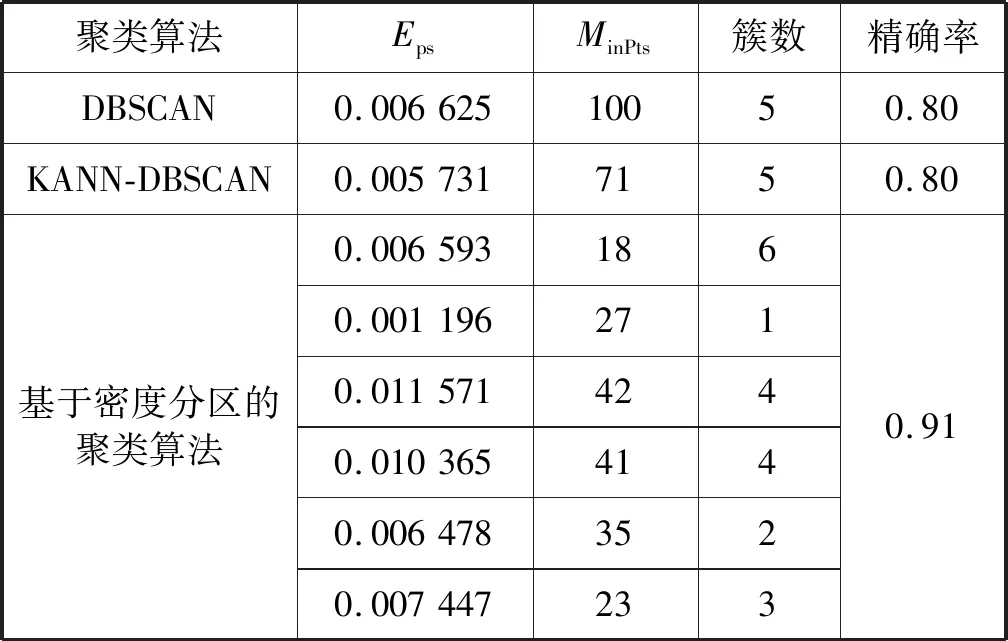
表4 参数选取和聚类结果分析

从参数选取方面对比可知,DBSCAN聚类算法的参数需要依靠人工经验确定,上述参数在MinPts一定的情况下,以0.01为初始值,5×10-6为步长,需经过18 675次调参得出。KANN-DBSCAN算法和基于密度分区的聚类算法则可以通过计算自适应得到最优参数。

从聚类结果方面对比可知,本文算法的精确率有所提高,主要因为在针对数据密度分布不均匀情况下,无论是DBSCAN聚类算法还是KANN-DBSCAN算法,两者均采用全局参数,得出的结果只能反映研究范围内最热门的乘车区域,无法精确地反映出再往下一级的热门乘车区域。但这并不符合实际情况,如果出租车都集中于图8(b)和图8(c)所示的热门区域,这不仅会造成打车供需的不平衡,还会导致交通拥堵,反而得不偿失。基于密度分区的聚类算法很好地解决了这一问题,针对同一等级的局部密度自适应生成对应的局部参数,进行局部数据的聚类后合并,聚类的结果如表4所示。基于密度分区的聚类算法共生成20个簇,也就是20个相对热门的乘车区域,相较于其他两种算法,对全城出租车的调度、平衡乘车供求都具有一定的积极作用。但也由于该算法是针对局部密度进行讨论,所以在时间复杂度方面并未有所提高。

3.5 实验结果展示

基于上述研究内容,对工作日和非工作日的各时段载客高峰期进行基于密度分区的聚类分析和结果展示。

(1) 工作日各时段载客高峰期聚类结果。工作日各时段载客高峰期经过基于密度分区的聚类分析,具体聚类分析结果如表5所示。

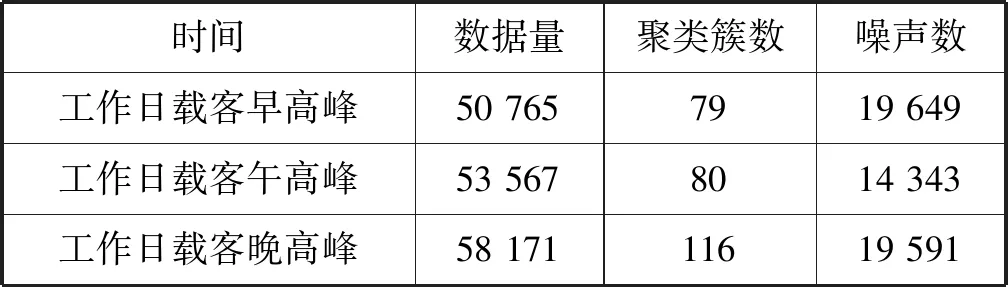
表5 工作日载客高峰分析结果

可以看出,工作日每时段载客高峰期对应的数据量即为载客次数,聚类簇数为出租车载客热点区域数,噪声数则为非载客热点区域的载客次数。其中,早高峰和午高峰的热点区域数量较为相近,除了载客量上的变化,更多的是因为工作日白天出行主要是为了上班和上学等,出行热点区域较为固定。晚上出行更多的是个人因素,可供选择的目的地增多,出行热点区域也随着增多。而在非载客热点区域,则是早高峰和晚高峰载客次数较多。

(2) 非工作日各时段载客高峰期聚类结果。非工作日各时段载客高峰期经过基于密度分区的聚类分析,具体聚类分析结果如表6所示。

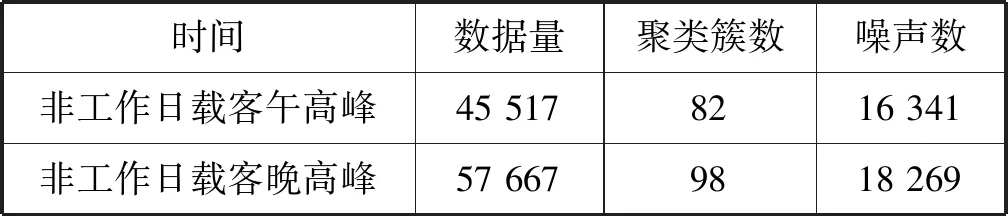
表6 非工作日载客高峰分析结果

可以看出,相较于非工作日载客午高峰的载客热点区域数量而言,非工作日载客晚高峰的载客热点区域增加了16个,较多为三环附近的居民区。其次,非载客热点区域也是晚高峰载客的可能性更高。

综上所述,基于工作日和非工作日载客高峰期的实验数据,实现了基于密度分区的聚类分析,其聚类结果不仅验证了出租车载客高峰期空间特征分析结果的准确性,并更进一步精确细化了载客热点区域,以及在非载客热点区域,早晚高峰期时段的载客率更高。

4 结 语

随着经济的快速发展和居民生活水平的提高,城市居民选择出租车作为出行方式的需求量增加,随之出租车行业规模也逐渐扩大且管理也愈加规范。但是为了进一步提高资源的利用率,减少乘客乘车的等待时间,基于成都市出租车的历史轨迹数据的处理与分析,得到结论如下。

(1) 出租车GPS原始轨迹数据集预处理。为了保证下一步数据分析结果的准确性,对出租车原始轨迹数据集进行数据清洗、筛选有效载客行驶时长和范围、载客点提取、坐标转换。

(2) 出租车载客行为时空特征分析。基于预处理后的出租车载客上车点轨迹数据集,从时间和空间两方面,分析得到出租车载客高峰时段和载客特点,以及每时段出租车载客空间分布特征。为出租车载客热点区域的分析提供依据。

(3) 出租车载客的热点分析。针对出租车轨迹数据密度分布不均匀的特点,提出基于密度分区的聚类算法,有效提高了载客区域分布的精确度。

此次研究仅对载客热点区域进行挖掘,没有考虑出租车载客其他影响因素。结合自然环境、网约车发展等各方面影响因素,建立不同因素影响模型,是下一步出租车轨迹数据的研究重点。