基于改进AdaBoost的梯田提取方法研究

康 洋 任 洁 全 凯 杨江涛 张宏鸣*

1(西北农林科技大学信息工程学院 陕西 杨凌 712100)

2(西北农林科技大学水利与建筑工程学院 陕西 杨凌 712100)

0 引 言

梯田是一种沿等高线方向修建的台阶式田地,在提高粮食产量、治理水土流失等方面具有重要作用[1]。因此,如何快速准确地对区域内梯田分布信息进行提取,对区域生态规划以及自然灾害的预防具有重要的作用与意义。长期以来,采用人工统计的方法来提取梯田分布信息效率低并且精度不高[2]。随着无人机遥感影像的发展,结合高分辨率遥感影像进行地物分布信息提取,逐渐成为当前研究热点话题之一。总结目前梯田提取的研究进展,主要分为基于窗口与基于对象两种方法。

基于窗口的提取方法,利用影像的纹理特征以及灰度特征,以像素窗口为最小单元进行梯田分布信息提取。Sofia等[3]采用改进的直线线段检测算法结合数字高程模型(Digital Elevation Model,DEM)对梯田信息进行提取。Crommelinck等[4]将梯田影像分割为若干个不重叠区域,进行边缘检测以及边缘连接,进行梯田提取。Zhang等[5]通过对高分辨率梯田遥感影像的边缘检测生成二值图像,再采用模板匹配法来对梯田区域进行提取,但模板尺寸固定,未能对梯田研究区域取得一个较好的结果。

基于对象的提取方法,通过多尺度分割将梯田影像转化为多个样本对象,结合纹理特征、光谱特征、形状特征等,充分利用相关地形信息来进行梯田分布提取。Capolupo等[6]基于DEM以及多光谱数据,采用坡度、地形位置指数与最小差异指数作为分类特征对梯田进行提取,由于研究区域有较多的植被覆盖,提取结果受到一定的影响。Eckert等[7]将高光谱数据与数字地表模型(Digital Surface Model,DSM)相结合,采用SVM算法来进行提取。薛牡丹等[8]将地形因子与无人机获取的高分辨率遥感影像融合后进行梯田提取,结果表明遥感影像与地形因子结合后,提取效果有了较大的提升。杨亚男等[9]将无人机正射影像与坡度数据进行融合,对梯田进行粗边缘与精细边缘提取,结果表明加入坡度数据后,梯田粗细边缘的提取效果都有了较大的提升。

基于窗口的提取方法在提取时考虑到了梯田的纹理以及灰度特征,利用了较少的地形信息,未结合更多含有丰富地形信息的地形因子来进行梯田提取。基于对象的提取方法利用了地形因子来进行提取,提取效果有了较大的提升,但目前对于复杂区域的提取未能取得较好的结果。

针对当前梯田提取算法在复杂地形区域提取时,算法适用性较差导致效果差异大的问题,本文采用改进AdaBoost算法,通过集成多个分类器共同决策,有效地提高了算法的适用性,对复杂地形区域取得了较好的提取结果。首先将无人机获取的高分辨率正射影像与DEM衍生的地形因子进行融合,利用多尺度分割算法获得三块不同地形特征的样本数据集。然后为保证数据特征的有效性,通过过滤式特征选择算法去除冗余特征。同时考虑到梯田和非梯田数量有着较大的差异,为降低不均衡数据对梯田提取结果的影响,对样本进行均衡化处理。最后利用改进AdaBoost提取方法对复杂的区域进行梯田提取。为了评价改进AdaBoost算法的梯田提取效果,本文将结合AdaBoost算法、SVM、KNN、CART进行对比验证。

1 研究区域与数据基础

1.1 研究区域与数据获取

1.1.1研究区域

研究区域为甘肃省榆中县龙泉乡,地理上的坐标范围为东经104°10′58″至104°19′51″,北纬35°34′4″至35°40′56″,本文选取了三块不同特征的区域进行研究。区域1中有部分山脊以及道路,梯田田块主要呈条状,具有细、窄的特点,数量较多,为密集条形区梯田。区域2中有部分道路以及少量建筑物,形状不规则,为不规则区梯田。区域3中有部分建筑物以及山脊,主要呈块状,并且边缘曲线光滑,数量较少,为稀疏块状区梯田。

1.1.2数据获取

为降低天气因素的影响,于2016年3月对研究区域利用无人机搭载相机来进行数据采集,所拍摄的单幅影像的采集面积约为340 m×500 m,影像分辨率为0.5 m,采集时长约24小时。为了保证采集过程中精度符合要求,对梯田边缘以及道路的交叉处设立地面的控制点,并实时进行空间运算和精度检测。通过Agisoft PhotoScan软件对所获得的影像数据进行处理,对整个研究区域进行划分,并进行点云提取和立体模型的构建,合并后进行纹理提取,获取数字表面模型DSM,通过所获得的点云数据,得到地面点的DEM数据,分辨率为0.5 m。

1.2 数据预处理

本文首先对研究区域图像进行了去雾处理,然后将去冗余后地形因子与正射影像进行融合,得到富含地形信息的遥感影像,利用多尺度分割技术进行影像分割,获得用于梯田提取的样本数据集,最后对样本集进行特征选择、样本均衡化,降低冗余数据和不均衡数据对梯田提取结果的影响。

1.2.1图像去雾

物体的反射光线在大气中传播的时候会受到颗粒物等的影响,导致光线的传播方向被改变,向各个方向散射,最终所得到的图像会变得模糊,因此需要进行图像去雾[10]。目前主要采用暗通道去雾算法来进行图像去雾[11],暗通道去雾算法首先计算大气散射模型,得到透射率以及全局大气,然后根据暗原色先验理论在RGB三通道以及周围的局部区域取最小值,计算得到图像的透射率并估算全局大气,最终得到无雾图像[12]。

基于暗通道的去雾步骤如下：

(1) 计算大气散射模型,计算方法如式(1)所示。

I(x)=J(x)t(x)+A(1-t(x))

(1)

式中：I(x)为有雾图;J(x)为无雾图像;t(x)为透射率;A为全局大气,经变换可得式(2)。

(2)

(2) 暗原色先验理论如式(3)所示。

(3)

式中：Jdark(x)表示暗原色;y∈Ω(x)是以x为中心的领域区域。

(3) 得到图像透射率如式(4)所示。

(4)

估算全局大气A,代入式(2)得到无雾图像。

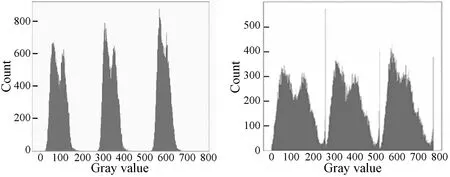
将去雾前的图像与去雾后的图像进行比较,去雾后的图像地物间的纹理差异更为显著,提升了图像的清晰度,可观察到更多的地物细节如图2所示。

本文对三块区域的原图以及去雾后图像的灰度直方图进行了分析如图3所示,可以看到原图直方图的能量分布较为集中,并未充分分布到整个颜色空间,经过去雾处理,能量分布较原图更加均匀,去雾后的图像可以提供更加有效的图像信息。

1.2.2基于相关性的地形因子降维

地形因子是指为有效研究与表达地貌形态特征所设定的具有一定意义的参数或指标[14]。

坡度S、粗糙度TR、高程变异系数CVE、正负地形因子PN、山体阴影HS、坡度的坡度SOS均为常见地形因子,本文采用上述地形因子来进行计算,计算方法如下所示。

(1) 坡度S。反映坡面的倾斜程度,如式(5)所示。

(5)

式中：ΔH为高程差;L为水平距离。

(2) 粗糙度TR。刻画地表地势的起伏变化,如式(6)所示。

(6)

式中：α为投影角度;SAB为表面积;SAC为投影面积。

(3) 高程变异系数CVE。表示地表高程变化,如式(7)所示。

(7)

式中：SD为标准差;Hmean为平均高程。

(4) 正负地形因子PN。描述基本的地貌形态,如式(8)所示。

PN=Hmax-Hmean

(8)

式中：Hmax为最大高程值;Hmean为平均高程值。

(5) 山体阴影HS。模拟光源在某方向和太阳高度下的灰度图,如式(9)所示。

HS=255×cos(zenithrad)×cos(sloperad)+

sin(zenithrad))×sin(sloperad)×

cos(azimuthrad-aspectrad)

(9)

式中：sloperad为坡度弧度数;azimuthrad为光线方向角的弧度数;aspectrad为坡向弧度值;zenithrad为太阳天顶角的弧度数。

(6) 坡度的坡度SOS。为坡度的坡面倾斜度,如式(10)所示。

(10)

式中：SΔH表示高程差;SL为水平距离。

计算最终得到6个地形因子如图4所示。

考虑到地形因子间数据冗余对梯田提取的影响,本文通过PCA得到地形因子间的相关系数,通过设立阈值来进行相关性强弱判断,去除冗余地形因子,方法的步骤如下：

(1) 计算地形因子。通过DEM数据计算衍生的6个地形因子。

(2) 基于PCA的地形因子相关系数估算。通过PCA将数据用线性无关的形式来进行表示,得到数据中相关性较低的分量[13]。本文通过PCA中地形因子的相关系数矩阵来进行后续的降维。

(3) 设置相关系数阈值。采用皮尔逊相关系数来进行相关系数的计算,设置相关系数阈值来进行地形因子相关性强弱的判断。

(4) 基于阈值的地形因子选择。对比分析相关系数,结合阈值确定获得用于梯田提取的地形因子。

表1-表3分别为三块研究区域经过PCA后的地形因子相关系数矩阵,矩阵中的值表示两个地形因子的相关系数,当相关系数的绝对值越接近于1或-1时,表明地形因子间的相关性越强。本文采用皮尔逊相关系数来进行相关系数计算,皮尔逊相关系数是一种常见的相关系数计算方法,当相关系数的绝对值大于0.8时,表明地形因子间具有强相关性。通过对三块研究区域地形因子相关系数判断,最终得到用于梯田提取的地形因子为S、TR、HS、SOS。

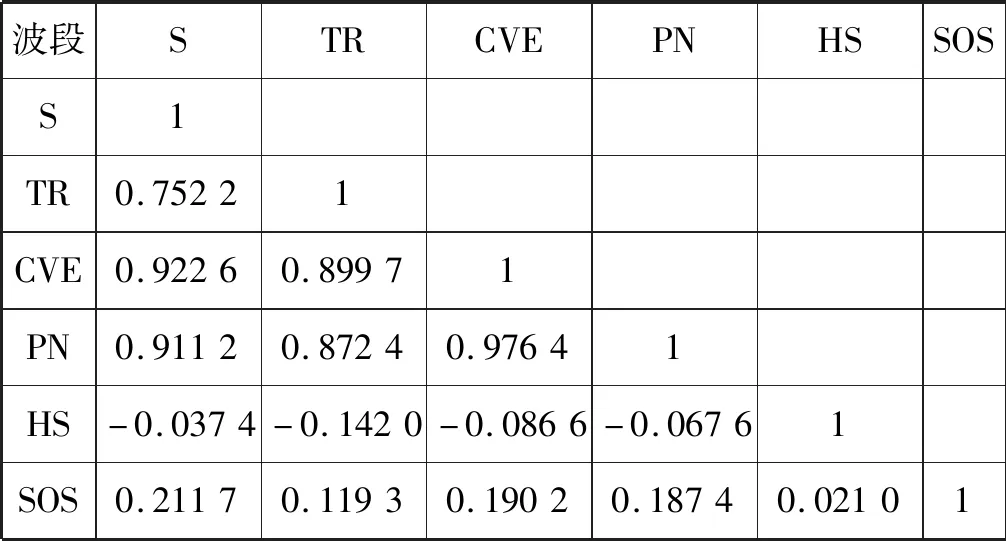
表1 区域1 PCA相关系数矩阵

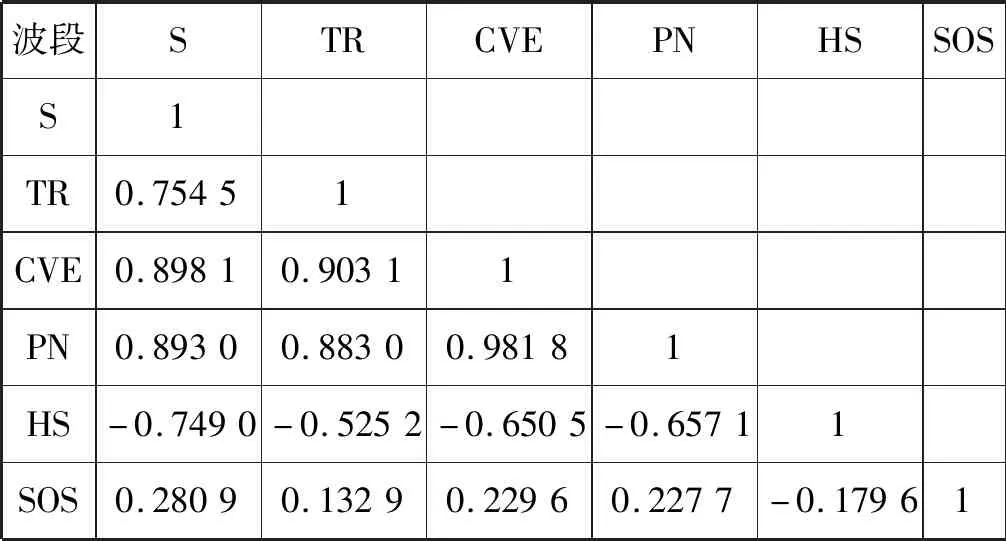
表2 区域2 PCA相关系数矩阵

1.2.3多尺度分割

为了获取样本数据集,需要对研究区域影像进行分割得到多个分割区域,并且满足区域内相似性高,而区域间相似性低的要求[15]。多尺度分割是一种常见的分割方法,采用自下而上的策略,单独的像元在最小异质性准则之下与相邻的像元逐渐进行合并,通过控制分割尺度、形状异质性、光谱异质性来确定分割中所生成对象的形状与数量。分割尺度过小会造成欠分割现象,会将完整的对象分割得支离破碎,尺度过大会造成过分割现象。将不同的对象划分为一个整体[16],形状异质性通过紧致度因子和光滑度因子来进行表示,最终实现在分割尺度阈值下达到平均异质性最小。异质性的度量如下：

(1) 总体异质性度量,如式(11)所示。

f=α·hshape+(1-α)hcolor

(11)

式中：f为影像对象总体异质性;hshape为光谱异质性;hcolor为形状异质性,α为形状异质性所占权重,范围为[0,1]。

(2) 形状异质性度量,如式(12)-式(16)所示。

(12)

(13)

式中：hsmooth为光滑度因子,表示对象轮廓的光滑程度;hcompact为紧致度因子,表示对象的紧致程度;c表示区域的周长;l表示最小外接矩形的周长;s表示面积。

将相邻两个区域进行合并,c、l以及s分别为c1、c2、l1、l2、s1、s2,合并后光滑度因子和紧致度因子计算如下：

(14)

(15)

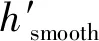
最终形状异质性表示为：

(16)

式中：hshape为形状异质性;α为光滑度因子权重值,范围为[0,1]。

(3) 光谱异质性度量,如式(17)所示。

(17)

式中：hcolor为光谱异质性;c为波段数;ωc为层的权重;σc为波段的方差。

将相邻两个区域进行合并,面积和方差分别为s1、s2、σc1、σc2,合并之后区域的面积和方差为smerge、σcmerge,则合并后的光谱异质性为：

(18)

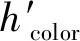
为了解决目前多尺度最优分割尺度人为操作的问题,本文采用ESP2方法来进行多尺度分割,通过评价不同尺度下分割结果的最大异质性[17],并根据影像分割结果局部方差(LV)及ROC曲线来对分割的最优尺度进行评估,利用ROC的峰值来反映最大异质性[18]。由于影像所含地物复杂,通过ESP2计算可得到多个最优尺度,ROC的计算如式(19)所示。

(19)

式中：LVL分割尺度为L时分割结果的局部方差均值;LVL-1为分割尺度为L-1时分割结果的局部方差均值。

首先将原始正射影像融合4波段地形因子影像,形成7波段遥感影像,然后设置ESP2的分割参数,利用控制变量法选择出分割效果较好的形状异质性权重和紧致度因子,权重的参数组合为(0.2,0.5)。通过ESP2方法对区域1进行多尺度分割,ROC曲线会出现多个峰值如图5所示,其中黑色为局部方差,呈上升趋势,灰色为ROC曲线,随着尺度变化上下波动。

将所有峰值对应的尺度用于分割,对比选择出梯田的最优分割尺度。通过对比分析,确定区域1的最优分割尺度为70,与其他尺度的分割结果进行对比,在最优分割尺度时梯田提取效果较好,如图6所示,黑框为其他尺度存在欠分割与过分割的区域。

使用上述方法依次对区域2、区域3的分割尺度进行计算,最终得到最优分割尺度分别为65、76。通过多尺度分割获取样本数据集,经过专家标注,得到研究区域中梯田与非梯田的数量,如表4所示。

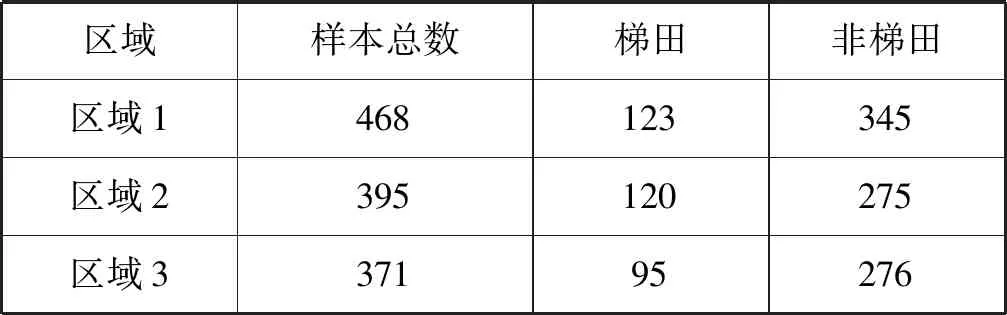
表4 研究区域样本数量

1.2.4特征选择

特征提取的优劣对最终的结果有着很大的影响[19]。本文从光谱、纹理、形状三个方面来对特征进行提取。光谱特征主要是对影像的相关灰度信息进行描述,选取均值和标准差作为梯田的提取特征。纹理特征通过图像的灰度变化来对粗糙度、方向性等性质利用灰度共生矩阵(Grey Level Co-occurrence Matrix,GLCM)来进行描述[20],选取同质性、对比度、非相似性等7个特征作为提取特征。形状特征通过几何参数来进行表达,选取形状指数和长宽比作为提取特征,如表5所示。

表5 特征描述

为降低冗余特征的干扰,采用CfsSubsetEval评估器,结合Best-First搜索方法来进行特征选择。首先Best-First搜索方法从空的子集开始进行前向搜索来添加特征,当连续添加多个特征时,性能仍然没有改进就结束对属性子集空间的搜索。基于相关性,采用CfsSubsetEval评估器对特征子集进行评价,通过各个特征的预测能力以及特征之间的相关性,建立特征评价器作为最优特征子集的选择标准。

区域1中最优特征子集包含12个特征,分别为Mean(R、G、B、S、SOS)、Sd(R、S)、Entropy(HS、SOS)、Correlation R、Angular 2nd moment SOS、Homogeneity HS。区域2中最优特征子集包含10个特征,分别为Mean(G、S)、Sd(B、S)、Correlation B、Dissimilarity TR、Entropy TR、Angular 2nd moment(G、TR)、Homogeneity R。区域3中最优特征子集包含9个特征,分别为Mean(G、SOS、TR)、Sd R、Correlation R、Entropy(HS、SOS)、Homogeneity(R、B)。

以区域1为例,采用箱线图对最优特征子集进行分析。箱线图是一种常用的数理统计方法,从宏观上展示数据的大概分布[21]。图7为最优特征子集中的特征在梯田与非梯田上的分布情况,结果显示两者的分布重叠部分较少,梯田与非梯田有明显的区分效果,将这些特征进行结合,有利于更好地对梯田进行提取。

1.2.5样本均衡化

考虑到本文的数据集为不均衡数据集,为了降低不均衡数据对提取效果的影响,要进行均衡化采样处理。目前针对不均衡数据的采样处理主要分为欠采样与过采样,欠采样通过减少多数类的样本数量来达到样本均衡的样本,但对总体的样本数据未能充分利用。过采样通过增加少数类样本的数量来达到样本均衡,可以充分利用所有的样本数据。SMOTE算法是一种常见的过采样算法,利用人工方式合成样本量较少的类,扩大样本量,保证不同类别的样本量达到均衡水平。SMOTE算法步骤如下：

(1) 对于样本总数为n的少数类,采用欧氏距离计算每个样本ai(i=1,2,…,n)距离最近的M个样本。

(2) 根据样本的不平衡率设置样本合成的倍率N,在M个样本中随机选取N个样本,对于每个被选取的样本与原来的少数类进行样本合成,如式(20)所示。

anew=a+rand(0,1)×(ai-a)

(20)

式中：anew为合成的少数类样本;rand(0,1)为在区间(0,1)之内随机生成数。

2 实验方法

2.1 AdaBoost算法

在目前的梯田提取中,不同的分类算法易受研究区域地形特征的影响,对于不同的研究区域未能全部取得一个较好的提取结果。AdaBoost算法是一种常用的集成学习算法,根据样本的权值变化不断更新基分类器的权重,最终得到一个性能较好的分类模型。首先对每个样本赋予相同的权值,然后选取当前误差率最小的基分类器计算其权值以及更新样本权值,分错样本会被赋予更大的权值,对这些样本着重进行训练,通过不断迭代直至满足迭代条件,得到最终分类模型。算法的步骤如下：

(1) 赋予每个样本初始权值相等,如式(21)所示。

(21)

式中：D1(i)表示在第1次迭代下第i个样本的权值;N为样本总数;i=1,2,…,N。

(2) 比较各基分类器的误差率,选择误差率最小的基分类器F用于此次迭代,如式(22)所示。

(22)

式中：t为迭代轮数;et为误差率;Ft(xi)为预测标签;yi为实际标签,取值范围为{-1,1}。

(3) 计算基分类器F所占的权值,如式(23)所示。

(23)

式中：αt表示F的权值。

(4) 对训练样本的权值进行更新,如式(24)所示。

(24)

式中：当样本分对时,yiFt(xi)=1,反之样本分错时,yiFt(xi)=-1。样本权值更新如下：

(25)

(26)

式中：Dt+1(i)+表示正确分类样本的权值;Dt+1(i)-表示错误分类样本的权值。

(5) 设置所采用的基分类器数量为迭代阈值T,对步骤(2)-步骤(4)进行迭代。

(6) 得到最终分类模型,如式(27)所示。

(27)

式中：Ffinal为最终模型,值为预测的分类结果。

AdaBoost算法通过不断的迭代进行训练,当某些样本被多次错误分类后,会导致这些样本的权值过大,分对样本会被赋予较小的权值。权值过大的样本会对后面的基分类器权值影响较大,导致基分类器过于关注这些异常样本,对最终模型的性能有所影响。

因此,为抑制分错样本的权值过快增长,将样本的分错次数引入权值的计算公式中,防止不同样本权值差异过大,从而提高模型的性能。

本文对AdaBoost算法中的分错样本的权值迭代,进行了改进,改进如式(28)所示。

(28)

式中：Dt+1(i)-′表示改进后的分错样本权值迭代;m为常数,通常大于样本迭代次数;n为样本分错次数。

由于权值的范围为(0,1),为了使更新后的权值小于之前的权值,需要满足权值逐渐增长,并且随着分错次数的增加,权值的抑制作用愈加明显。通过对权值增长的抑制,使得算法在训练过程中对分错样本权重的增长变得缓慢,算法的结果需要关注全局数据上的优化,避免了因为少数样本的正确率,导致全局的正确率下降。

2.2 精度评价指标

精度评价是指对于实际中的真值数据与分类后的结果进行对比,来确定分类的准确程度[22]。本文通过总体分类精度OA(Overcall Accuracy)以及Kappa系数来进行精度评价。总体分类精度通过总的样本数与分类正确的样本数的比值来表示。Kappa系数通过总的样本数量与混淆矩阵来进行相关计算,综合考虑了混淆矩阵中精确率、召回率等因素,能够全面地对分类精度进行反映[23],如式(29)、式(30)所示。

(29)

(30)

式中：N代表总的样本数;n代表分类的所有的类别数;hik表示混淆矩阵中元素。

3 结果与讨论

3.1 最优基分类器数量选择

为了探究基分类器数量对分类精度的影响,本文采用不同基分类器数量进行实验,测试了基分类器数量从20到500共13组下的三块区域的分类精度和Kappa系数值,实验结果如图8-图9所示,可以看出三块区域的分类精度以及Kappa系数随基分类器数量增长上下波动,而且三块区域分类精度以及Kappa系数最高时对应的基分类器数量不同,表明了不同类别区域的数据特征不同。

本文以决策树为基分类器,通过不断改变基分类器数量观察精度的变化趋势,当三块研究区域的基分类器数量分别为80、360、200时,总精度与Kappa系数均达到最大,总精度分别为95.19%、93.67%、90.54%,Kappa系数分别为0.879 4、0.846 8、0.777 3。

3.2 SMOTE均衡化结果

为验证样本均衡化对梯田提取效果的影响,本文对三块研究区域分别进行实验,在未均衡化处理前,三块研究区域的不平衡率分别为2.96、2.12、2.91。均衡化前后的精度以及Kappa系数如图10所示,结果表明,经过样本均衡化后,各个模型性能均有所提升,并且改进的AdaBoost算法提取效果最好。

(a) 区域1原图 (b) 区域2原图 (c) 区域3原图

(a) 区域1原图 (b) 区域1去雾后

(a) S(b) TR (c) CVE(d) PN (e) HS (f) SOS图4 研究区域的地形因子

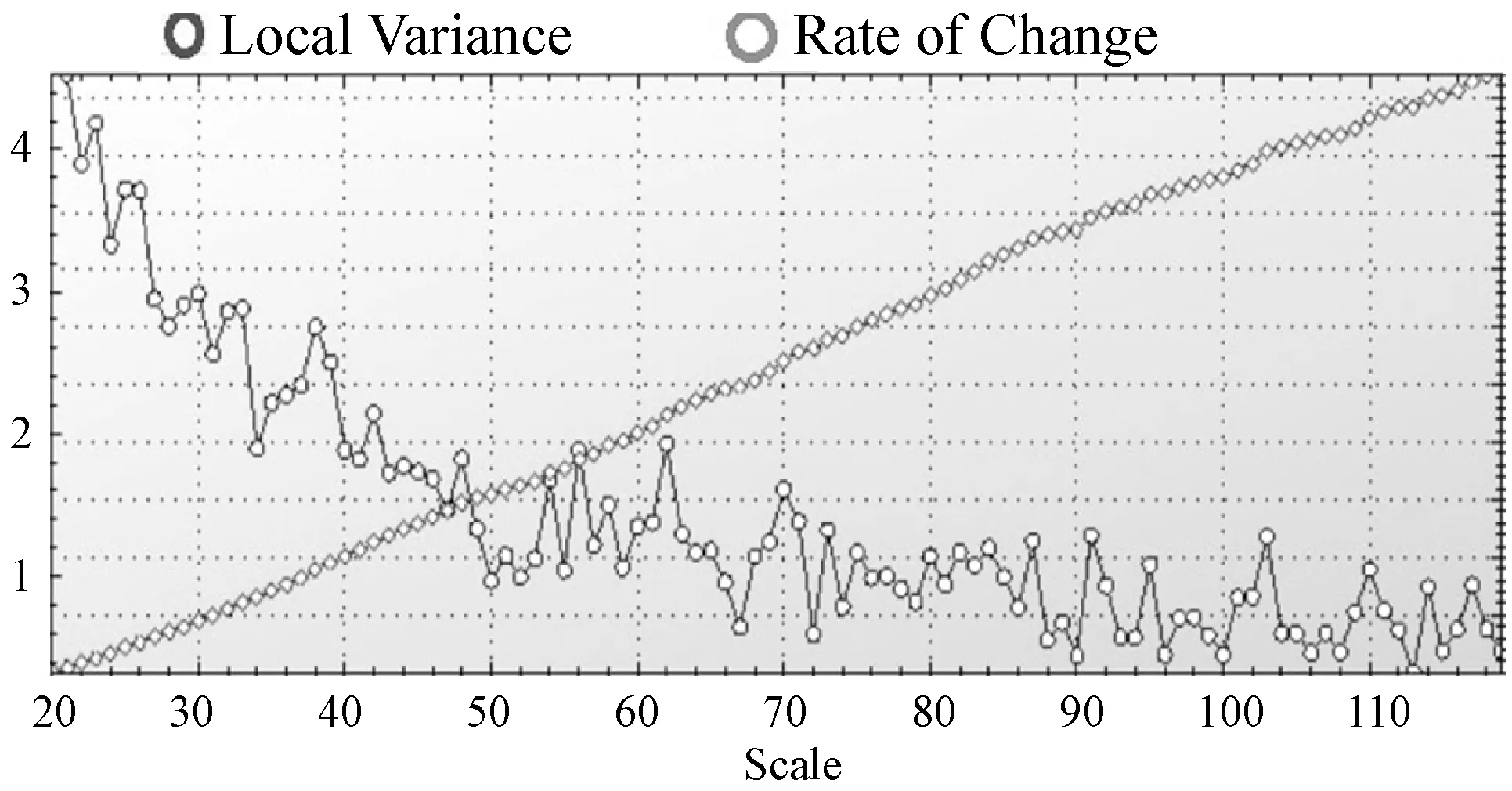
图5 区域1 ESP2结果图

图6 区域1多尺度分割结果对比

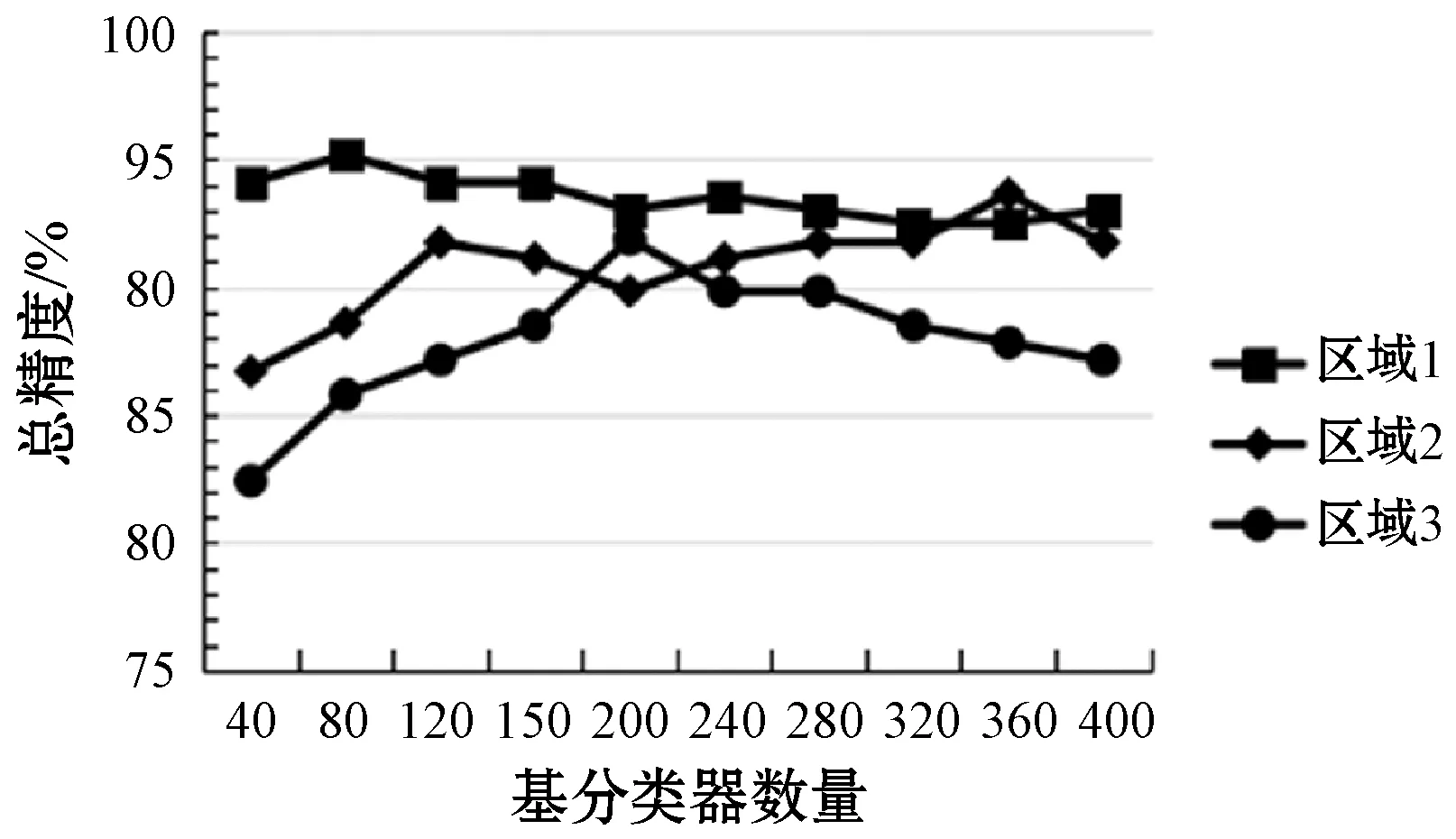
图8 不同基分类器数量下的总精度

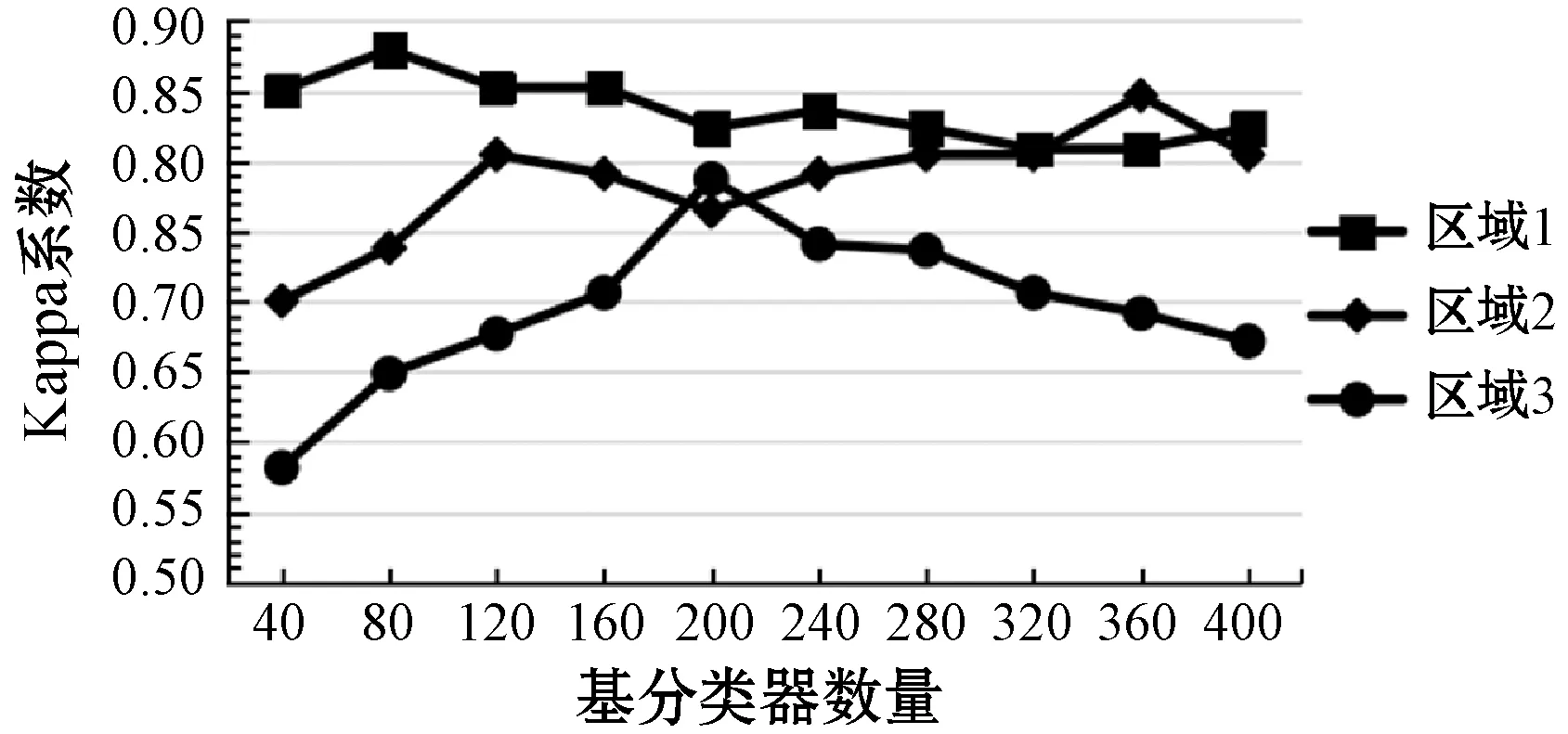
图9 不同基分类器数量下的Kappa系数

(a) 区域1总精度对比 (b) 区域1 Kappa系数对比

3.3 梯田提取结果

为了验证本文方法的有效性,与AdaBoost算法以及KNN、SVM、CART进行对比实验。对密集条形区、不规则区、稀疏块状区区域进行梯田提取。为了对比不同算法的提取效果,结果中用灰色表示梯田区域,白色表示非梯田区域,黑色表示提取错误的区域。

区域1为密集条形区梯田,梯田区域多为条状,并且具有细窄的特点。不同算法的提取效果如图11所示。在三种常用的分类算法KNN、SVM、CART中,CART在宽短类型梯田区域提取效果较差。KNN的提取效果优于CART,但对于细长类型的区域如道路等提取效果较差。SVM的提取效果优于前两种方法,但对于临近道路的复杂地物区域提取效果差,相比而言,AdaBoost算法对于宽短类型、细长类型以及临近道路的复杂地物区域的提取效果优于以上三种方法。改进的AdaBoost算法的提取效果优于AdaBoost算法,对于地势较高的区域提取效果更好,同时避免了其他方法对小面积非梯田区域的错误提取。

(a) 真值图 (b) 改进AdaBoost (c) AdaBoost

区域2为不规则的梯田区域,梯田形状不规则。不同算法的提取效果如图12所示。KNN、SVM、CART三种方法的提取效果的差异较小,对于小面积区域以及连通梯田的非梯田区域提取效果较差。AdaBoost算法对于细窄区域的提取效果较差。

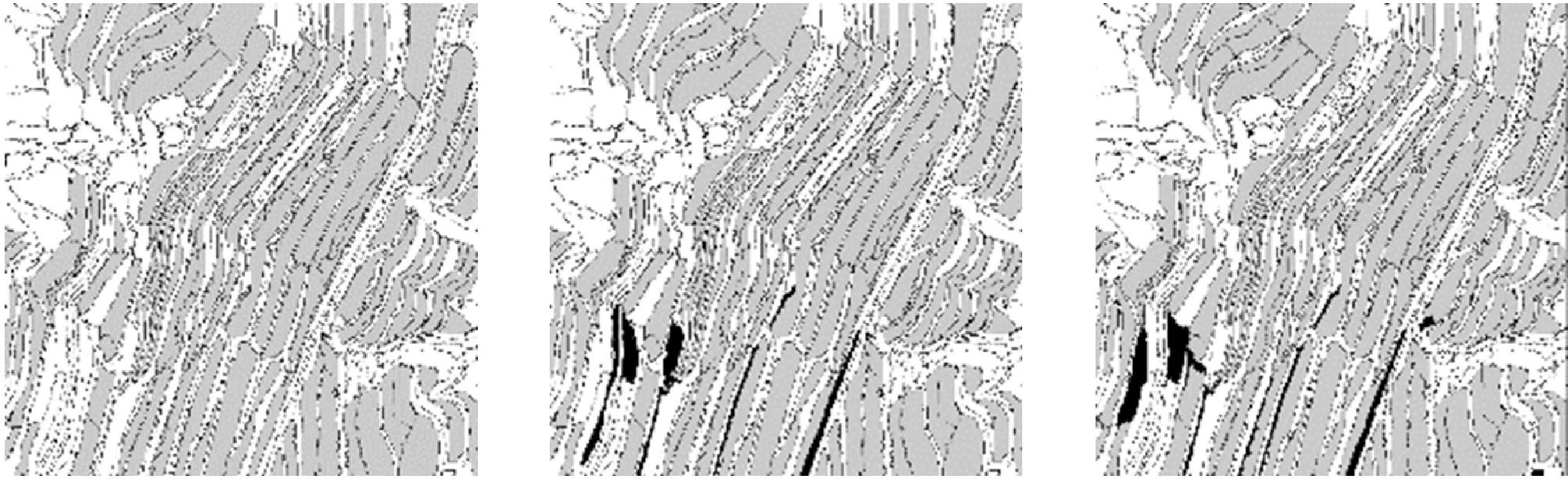
(a) 原图 (b) 改进AdaBoost (c) AdaBoost

区域3为稀疏块状梯田区域,边缘光滑,数量相对较少,梯田面积较大,部分区域由于积雪的覆盖,导致梯田纹理颜色等发生变化不能较好地进行提取,并且田坎对提取也会产生影响。不同算法的提取效果如图13所示。KNN、SVM、CART三种算法对于积雪覆盖的区域均不能取得较好的提取效果,改进的AdaBoost算法以及AdaBoost算法在积雪覆盖区域与上述三种方法相比,提取效果较好。但AdaBoost算法相对于改进的AdaBoost算法,对于含有建筑物的区域提取效果较差。

(a) 真值图 (b) 改进AdaBoost (c) AdaBoost

从以上实验结果可以看出,改进的AdaBoost算法以及AdaBoost算法较KNN、SVM、CART三种方法具有更好的提取效果,而改进的AdaBoost算法对于较难提取的区域较AdaBoost算法具有更好的提取效果。

本文测试的五种方法在三块梯田区域上提取结果的总精度以及Kappa系数如表6-表7所示。改进的AdaBoost算法以及AdaBoost算法的总精度以及Kappa系数均高于KNN、SVM、CART三种算法,改进的AdaBoost算法的平均总精度以及平均Kappa系数相比于AdaBoost算法分别提高了1.62百分点以及0.04,表明改进的AdaBoost算法具有良好的提取效果。

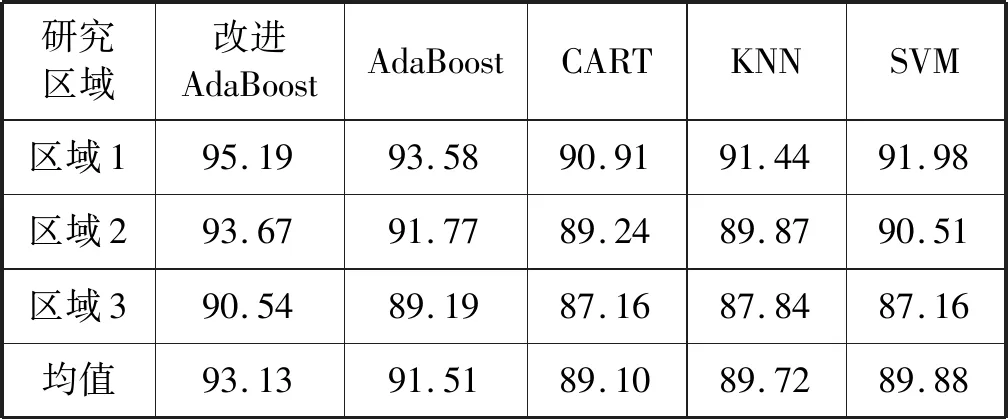
表6 研究区域梯田总精度提取结果(%)

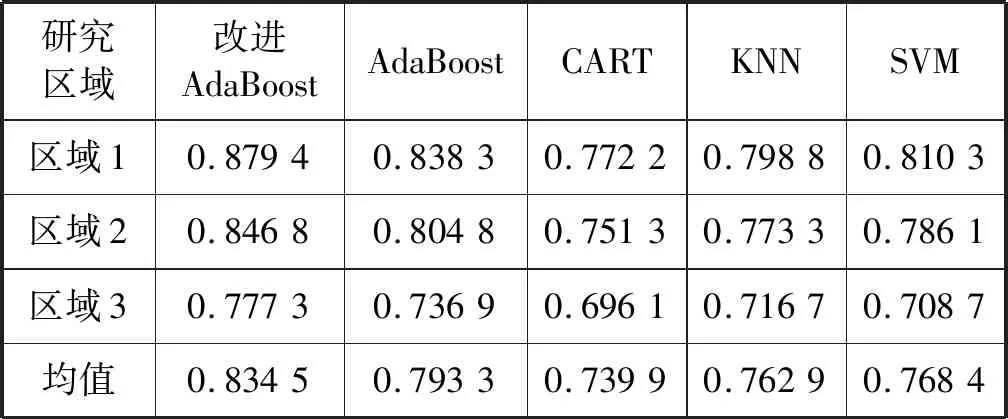
表7 研究区域梯田Kappa系数提取结果

4 结 语

本文改进的AdaBoost算法结合SMOTE均衡化,对三块不同地形特征区域进行梯田提取。首先对高分辨率遥感影像与地形因子进行融合与分割,得到样本数据集;然后通过特征选择对冗余特征进行去除,提高了特征的有效性;针对研究区域梯田与非梯田样本不均衡问题采用SMOTE均衡化,结果表明,样本均衡化对梯田提取有一定影响;最后对五种方法的提取结果进行分析,表明改进的AdaBoost算法对复杂区域的梯田提取有较好的效果。

在下一步的研究中,将采用不同类型的算法作为AdaBoost算法的基分类器进行研究,以及与深度学习进行结合来探索更为精确的梯田提取方法。