基于混合烟花算法的两级车辆路径优化研究

熊国文 张 敏,2 张训杰 张则强,2

1(西南交通大学机械工程学院 四川 成都 610031)

2(西南交通大学轨道交通运维技术与装备四川省重点实验室 四川 成都 610031)

0 引 言

城市交通机动车数量增加、道路状况、环境变化等因素,往往会引起车辆行驶缓慢,进而造成交通拥堵[1-3]。而影响交通拥堵的因素随着时间和空间的改变而动态变化,即在不同时段,同一路段车辆速度不一定相同;在同一时段,不同路段车辆速度也不一定相同[4]。动态交通状态导致物流配送体系存在诸多不确定因素[5]。如遇到交通状态恶劣,会直接影响物流配送的效率,进而超出客户时间窗,造成延时配送、成本增加、客户满意度下降等问题。因此,如何根据动态交通状态规划高效的物流配送车辆路径,是物流企业亟待解决的问题。

基于动态交通状态的物流配送车辆路径问题是车辆路径问题的延伸,旨在动态的交通状态下规划出最佳的物流配送方案。其中如道路条件、交通流量、意外事故、天气情况等动态交通信息,对动态车辆路径问题的解决起着非常重要的作用[6]。近年来,随着通信和信息技术发展,动态交通信息可通过相应的平台快速有效地获取和处理[7],为研究动态车辆路径规划提供了先决条件。如Xiao等[8]认为车辆行驶速度主要由交通和路况决定,首先从相关信息系统获得交通数据计算车辆在各路段的平均速度,在此基础上建立以温室气体排放量最小为目标函数的混合整数规划模型。针对动态交通影响物流配送效率,进而超出客户时间窗,Ghani等[9]研究了交通拥挤导致不必要的时间延误,从而造成客户损失。同时,相关学者研究了动态交通物流配送车辆的异构问题,即不同的车辆载重能力、行驶里程等约束不同,如张传琪等[10]将路网拥挤状态沿时间轴展开,构建了考虑服务途中动态拥挤的多车型车辆路径模型,设计了求解该模型的改进遗传算法。上述文献皆对动态交通状态下的车辆路径问题进行了研究并取得了可喜的成果,但未考虑客户之间可能存在多条连通路线以及计算车辆在各个路段上的理论行驶时间可能与实际行驶时间相差较大等问题。基于此,李顺勇等[11]针对城市路网中的两节点之间具有多条连通道路的特性研究动态车辆路径规划问题,建立了多通路时变网络下的低碳车辆路径优化模型。Alinaghian等[12]通过考虑车辆装载量、速度、道路梯度和城市交通等因素,分析了多路径选择对时变车辆路径问题的重要性,提出了一种基于高斯萤火虫算法的改进算法,以找到油耗最小的最优路径。

目前,大多数学者的研究主要集中在单级物流配送车辆路径优化上,但在实际物流配送中,为了避免大型车进入城市造成污染,很多城市采取车辆限行政策,两级物流配送模式广泛应用于各种场景下的商品配送[13-14],即商品先由大型车运输至各个中转站,再由小型车运输至该中转站所服务的各个需求点[15-17]。若两级物流配送车辆路径的优化仍然采用优化单级物流配送车辆路径的方法,自上而下优化每一级物流配送车辆路径,则无法实现两级物流配送车辆路径的整体优化。近年来,越来越多的学者开始从事两级车辆路径问题(Two-echelon Vehicle Routing Problem,2e-VRP)的研究。曾正洋等[18]先将货物从中心仓库配送至城市外围的中转站,再转运至需求点,同时,考虑到将部分或全部运输任务分配给第三方物流公司,第一级车辆在完成配送任务后无须返回中心仓库,或者必须原路返回,构建了开闭混合式两级车辆路径问题的数学模型。张汉鹏等[19]研究应急物资配送中的两级车辆路径决策策略与应急物资配送绩效问题。但两级车辆路径问题的研究中较少考虑关于物流节点之间有多条连通路线、动态的交通等现实物流配送情况。

自两级车辆路径提出以来,学者和专家提出了不同的求解算法。Wang等[20]针对具有随机需求的两级容量车辆路径问题,提出了一种基于遗传算法新的求解方法。Li等[21]考虑碳排放量,研究两级长途运输系统中的车辆路径优化问题,提出了一种改进的局部搜索阶段的Clarke和Wright节约启发式算法(CW),有效降低二氧化碳的排放量。Hemmelmayr等[22]针对两级车辆路径问题和位置路径问题,提出了一种自适应大邻域搜索启发式算法。胡乔宇等[23]研究了客户需求随机的两级车辆路径问题,设计了一种基于蒙特卡洛仿真优化方法,将仿真过程嵌入到启发式算法的邻域搜索过程进行求解。Belgin等[24]研究了两级同时取送车辆路径问题,提出了一种基于变邻域下降和局部搜索的混合启发式算法。由于两级车辆路径属于NP-hard问题,求解比较复杂,难以同时确保求解速度和求解质量。为了解决此问题,本文结合烟花算法和遗传算法各自的优点,提出一种混合烟花算法,以提高收敛速度、降低迭代次数达到同时确保求解速度和求解质量。

鉴于上述有关两级动态物流配送车辆路径以及求解方法研究的不足,结合物流配送的实际情况,从车流量大小、道路施工情况、天气恶劣程度等动态交通因素分析对车速的实时影响,以车辆载重为约束条件,同时考虑客户时间窗,配送时间超出客户时间窗则产生惩罚成本,建立以物流配送总成本最小为优化目标的两级动态物流配送车辆路径优化模型。针对烟花算法收敛速度慢的缺陷,用插入法生成较优的初始种群,引入交叉操作提出一种新的混合烟花算法。通过计算两级车辆路径问题标准算例,与遗传算法和现有文献运算结果作对比,验证了算法的有效性和高效性。

1 问题与建模

1.1 问题描述与假设

两级物流配送系统包括一个配送中心、若干中转站和若干客户,两级物流配送的网络结构如图1所示,D点代表配送中心,S点代表中转站,C点代表客户点。客户所需商品首先由大型车从配送中心运输至各个中转站,然后由小型车将商品从中转站运输至各个需求点,要求其配送总时间在客户能接受的范围内,否则会产生较大的惩罚成本。其中大型车配送阶段称为第一级物流配送,由于中转站的需求可能大于车辆容量,因此,第一级物流配送属于需求可拆分配送,如图1中实线箭头所示;小型车配送阶段称为第二级物流配送,此阶段需求不可拆分配送,如图1中虚线箭头所示。为进一步切合实际物流配送,本文考虑动态交通对物流配送的影响,以及各个节点之间有多条交通状态不一致的连通道路,使该问题更加符合实际物流配送。

图1 2e-VRP网络结构

综合考虑带时间窗的两级动态物流配送特点,做出如下假设：(1) 每条配送线路上的客户需求量之和不能超过配送车辆的最大载重量Q1和Q2;(2) 第一级中转站货物可拆分配送,第二级需求点货物不可拆分配送,每级物流配送使用同一种车型;(3) 每个客户的需求数量必须得到满足且只能由一辆车配送;(4) 每辆车从配送中心或中转站出发,完成配送任务后返回到相应的配送中心或中转站;(5) 每项配送任务必须在客户要求的时间范围内完成,否则就会产生高昂的惩罚费用;(6) 车辆一旦确认了所服务的客户之后便不能再更改。

1.2 符号说明

根据以上假设,构建混合整数规划模型,设定模型参数与决策变量。

D：配送中心集合;

S：中转站集合;

P：需求点集合;

C：总成本;

c1：一级车辆单位距离运输成本;

c2：二级车辆单位距离运输成本;

c3：时间惩罚成本;

dij：节点i到节点j之间的距离;

Q1：一级车辆最大载重;

Q2：二级车辆最大载重;

U：一级车辆集合;

K：二级车辆集合;

qi：需求点i的需求量;

v1：一级车辆最大行驶速度;

v2：二级车辆最大行驶速度;

v1ij：一级车辆从节点i到节点j的实际速度;

M：一个足够大的数;

Ti：客户i能接受的最长配送时间;

es：中转站s的需求量;

Tsu：一级车辆u达到中转站s的时间;

Tik：二级车辆k达到需求点i的时间;

ti：到达客户i的时间;

Zsu：一级车辆u给中转站s的运输量;

riju：一级车辆u访问中转站i后访问j,riju∈{0,1};

xijk：二级车辆k访问需求点i后访问j,xijk∈{0,1};

yik：需求点i的需求量由二级车辆k配送,yik∈{0,1}。

1.3 数学模型

用具有代表性的车流量指数、天气恶劣指数、道路施工指数刻画交通状态,参数α1ij表示节点i到节点j的车流量指数,α2ij表示节点i到节点j的天气恶劣指数,α3ij表示节点i到节点j的道路施工指数。一级与二级车辆从节点i到节点j的实际速度由式(1)和式(2)求得。

v1ij=α1ij×α2ij×α3ij×v1

(1)

v2ij=α1ij×α2ij×α3ij×v2

(2)

一级物流配送车辆路径成本设为f1,则：

(3)

二级物流配送车辆路径成本设为f2,则：

(4)

配送延时惩罚成本设为f3,则：

(5)

目标函数：minC=λ1f1+λ2f2+λ3f3

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

tiu+dis/v1is+M×(1-risu)≥tsui∈D∪S,s∈S,u∈U

(17)

tiu+dis/v1is-M×(1-risu)≤tsui∈D∪S,s∈S,u∈U

(18)

tik+dij/v2ij+max(tsu)+M×(1-xijk)≥tju

s∈S,i∈S∪P,j∈P,k∈K

(19)

tik+dij/v2ij+max(tsu)-M×(1-xijk)≤tju

s∈S,i∈S∪P,j∈P,k∈K

(20)

ti=maxtik

(21)

上述模型中式(6)为目标函数,式(7)表示一级车辆不能超载;式(8)表示二级车辆不能超载;式(9-10)表示一级车辆路径连贯;式(11)和式(12)表示每个需求点由一辆二级车服务一次;式(13)保证中转站的需求量配送完成,式(14)表示每辆车从配送中心出发,经过若干需求点后回到配送中心;式(15)表示每辆车从中转站出发,经过若干需求点后回到出发的中转站;式(16)求出中转的货物需求量;式(17)-式(21)求货物到达需求点的时间。

2 算法设计

2.1 解的编码

本文采用实数编码,以多行序列形式表示上述问题的解,如图2所示,正方形代表配送中心,三角形代表中转站,圆形代表需求点。图2中解的含义是：配送中心需要两辆一级车为两个中转站配送货物,其路线是D-S1-S2-D和D-S2-D;中转站1需要两辆二级车为5个需求点配送货物,其路径是S1-8-5-S1和S1-3-7-6-S1;中转站2需要一辆二级车为三个需求点配送货物,其路径是：S2-2-1-4-S2。

图2 解的表示方法

2.2 插入算法

插入算法由Mole等提出[25],该算法的基本思想是将需求点依次插入到车辆中,每插入一个需求点都使得总成本增量最小,以此生成较好的解。为了增加初始种群的多样性,本文从需求点所有可插入的位置中,挑选成本增量较小的几个位置以概率Pi选择其中一个位置插入需求点。Pi由式(22)计算,其中：Cost_add(i)代表的是第i个位置的成本增量;I代表位置集合,为了避免选择成本增量较大的位置,对位置集合I设了限制条件,即当需求点可插入位置数量小于a时,位置集合I就是所有需求点可插入的位置集合,否则,位置集合I指成本增量从小到大的前a个对应位置集合,a的值可视情况而定,a越大,则初始解的多样性越好,但初始解的质量可能也会下降。

(22)

具体步骤如下：首先新建车辆,选择待插入的需求点,判断是否需要新建车辆,若需要则新建车辆,否则选择使得成本增量尽可能小的位置插入需求点,判断需求点是否插入完毕,没有则继续选择待插入的需求点继续插入,需求点插入完毕则生成个体。插入算法伪代码如下：

1V=[V1=[],V1_weight=0],k=2

2 fori=1：n

3point=Pi

4 ifVi_weight+q[point]>Q,i∈[1,2,…,k-1]

5V=[Vk=[],Vk_weight=0],k=k+1

6 forj=1：i×(k-1)

7cost_add(j)=0

8cost_add(j)=cost(V[j],point)+

cost(V[j+1],point)-cost(V[j],V[j-1])

9l=select(cost_add)

10m=vehicle(l)

11V=insert(l,point),

Vm_weight=Vm_weight+q[point]

12 Return个体

在上述伪代码中,V代表车辆集合,其中Vk代表的是第k辆车所服务的客户顺序,Vk_weight是第k辆车的载货量;P代表的是客户点集合,Cost_add(j)代表的是第j个位置的成本增量,Cost(V(j),Point)则是代表第j个位置对应的客户点Vh(j)与Point之间的成本,Select(Cost_add)选择成本增量尽可能小对应的插入位置,vehicle(l)代表位置l所在车辆,insert(l,Point)将客户点Point插入到第l个位置。经过插入算法可以得到总配送成本尽可能小的初始种群,同时,由于选择插入的位置不一定是成本增量最小的位置,使得初始种群多样化。

2.3 爆炸操作

首先通过式(23)计算烟花个体爆炸的火花数,然后针对个体的每辆车采用爆炸操作产生火花,爆炸操作如图3所示,随机选择两个位置,交换其对应位置的需求点编号,计算出爆炸后新车辆的配送费用,用配送费用最小的新车辆代替原来的车辆。

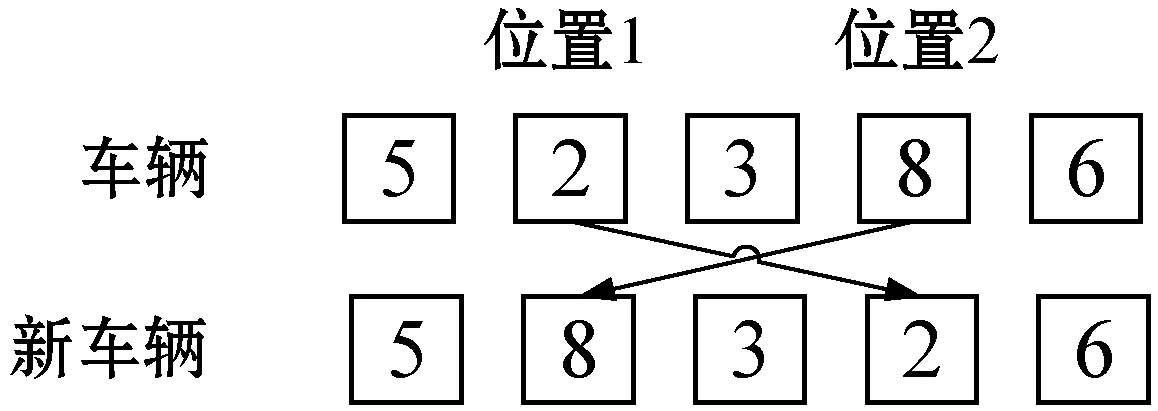
图3 爆炸过程

(23)

式中：Si为第i个个体产生的火花数;m是最大火花数量;F(i)是第i个个体的适应度值;Fmax=max{F(i)};ε为一个极小的常数,避免分母为零。同时,为了限制火花数量过多或过少,设定如下的产生火花数量的限制公式：

(24)

式中：round()为取整函数;a和b为给定的常数。

2.4 车辆交叉

首先求出群体最优解,然后用群体最优解中车辆的某一段需求点序列代替个体中的某一段相同长度的需求点序列,最后将重复的需求点删除,并且将没有被服务的需求点用插入算法重新插入到车辆中,形成新的可行解。车辆交叉操作如图4所示。

图4 交叉操作

2.5 算法流程

本文所提混合烟花算法,融入了插入法和交叉操作,保证了算法的全局搜索与快速收敛性能,首先采用插入算法生成较好的初始种群;其次计算适应度值并找出最优初始解;然后引入遗传算法中的交叉算子,使得烟花个体与最优烟花个体执行交叉操作;再利用烟花算法的爆炸算子产生爆炸火花,提高算法的寻优能力;最后采用精英策略保留较好的烟花个体进入下一次迭代。HFWA流程如图5所示,其中Gen为迭代次数。

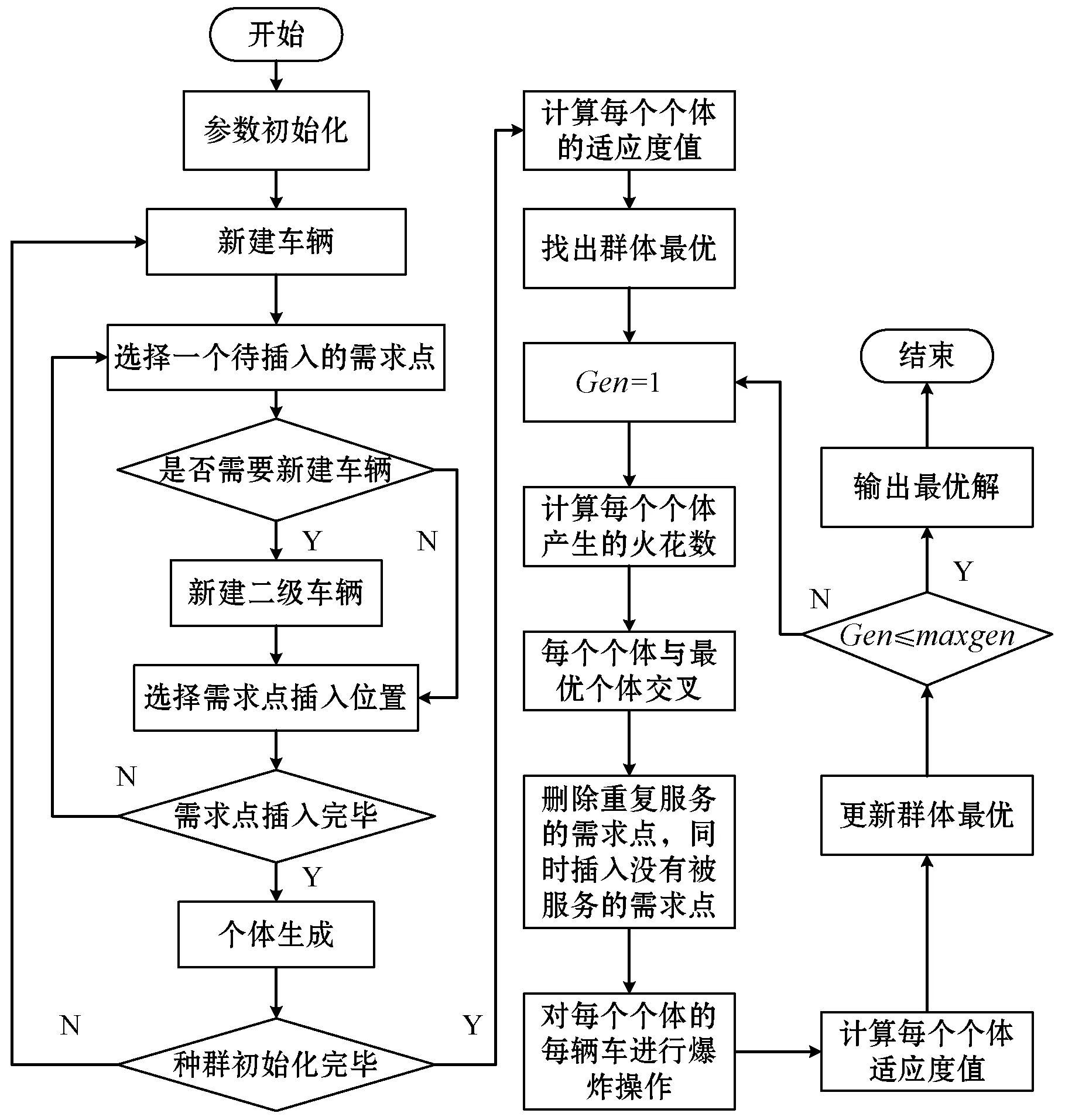
图5 算法流程

3 算法验证

本文使用2e-VRP标准算例对本文提出的HFWA进行可行性验证,标准算例以车辆行驶路径最短和使用车辆数最小为目标函数,车辆载重等为约束条件。标准算例数据来源于https：//www.univie.ac.at/prolog/research/TwoEVRP/。并将HFWA计算结果与官网给出的最优结果、GA、Marinelli[26]和Jie等[27]求解结果进行比较。其计算结果为使用Inter(R) Core(TM)i3-6100CPU@3.70 GHz处理器,仿真软件采用MATLAB 2010b。两种算法的种群规模都设置为200,HFWA迭代次数为50,GA迭代次数为500,计算10次的平均结果见表1。

对比表1中27个标准算例解的质量可见,GA仅能求出10个标准算例的最优解,其余结果与最优解相差较大。而HFWA有24个标准算例均能求出最优解,其余3个算例与现有最优解也相差较少。对比求解效率可见,由于HFWA使用了插入算法,设计较为复杂,提高了收敛速度,以降低迭代次数为代价提高求解效率,相较于GA在求解效率上快了1倍。而相较于文献[26]和文献[27]在求解质量与效率上同样具有优势。综上,证明了HFWA的可行性与良好的求解性能。

4 实 验

本文在标准算例(Set2a_E_n33_k4_s1_9)的实验数据基础上,通过随机生成客户点的时间窗演化为本文的实验数据(见表2)。随机生成了各个路段在各时刻的车流量指数、天气恶劣指数、道路施工指数(如表3所示,由于数据量太大,表3中仅仅列出前五个客户路段之间在某时刻的刻画交通状态的各项指数)。若某两个客户点之间的交通状态比较恶劣,从而使得物流配送成本急剧上涨,则会重新选择一条交通状况较好,路径不剧增的新路线,使得物流配送总成本变化幅度较小。

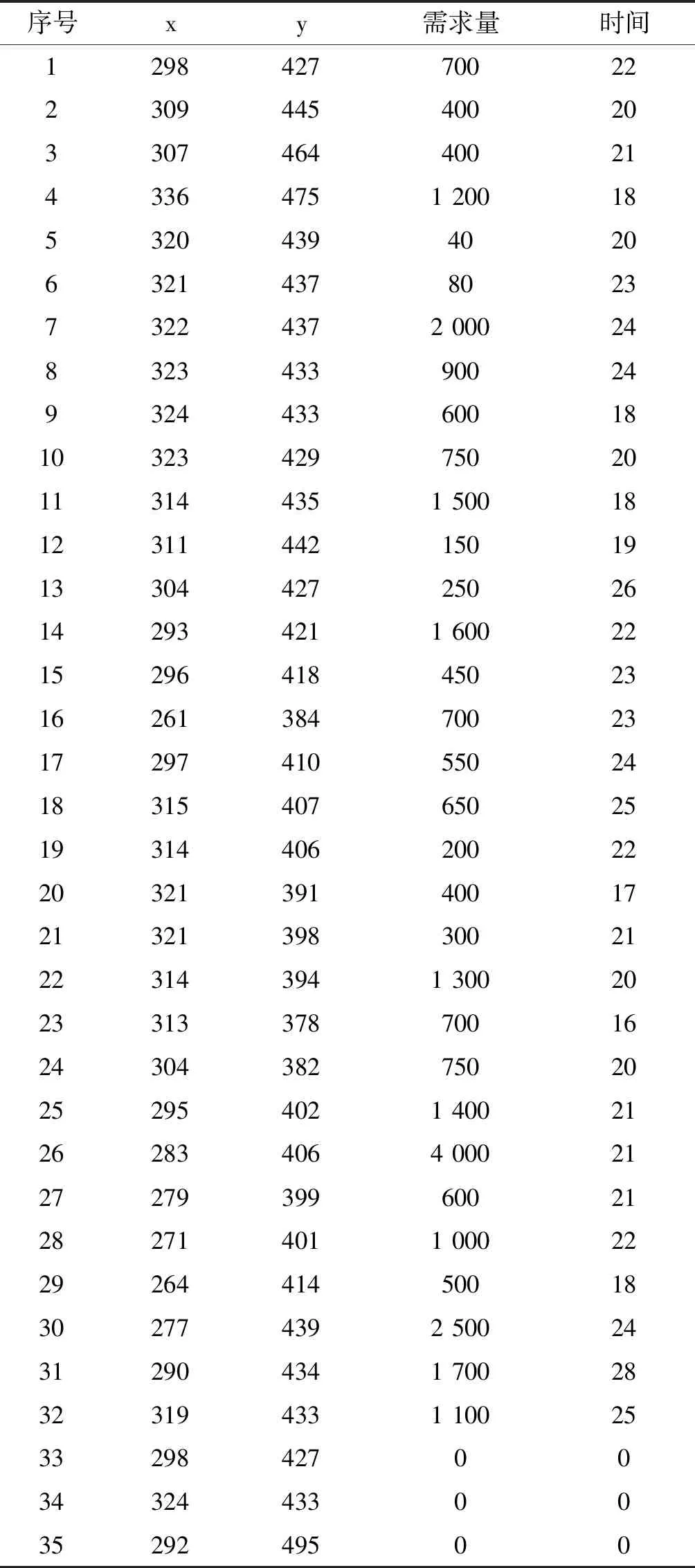
表2 实验数据

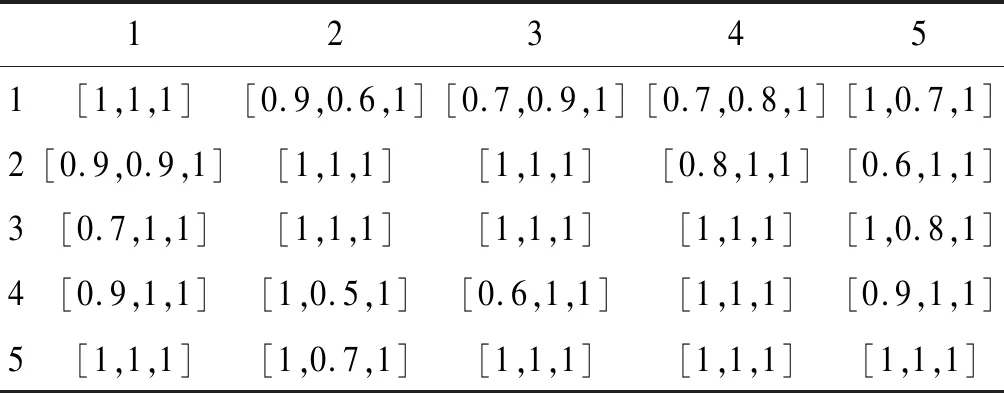
表3 交通状态指数

在表2中序号1至序号32为需要服务的客户点,客户点1和9被选择为中转站,为方便编码,将中转重新设置为33和34,35为配送中心。一级配送网络中使用载重量为20 000的大型车,二级配送网络中使用载重量为8 000的小型车。

为了说明在优化物流配送时,考虑交通状态的必要性,本文将不考虑交通状态条件下优化的车辆路径代入交通状态条件下得到的结果,与考虑交通状态下的优化结果进行对比分析。其车辆单位距离成本设置为1,延时惩罚成本设置为2,算法参数与求解标准算例一致。计算结果见表4,HFWA和GA优化后的两级车辆路径见图6至图9,其中实线表示第一级车辆路径,虚线表示第二级车辆路径。

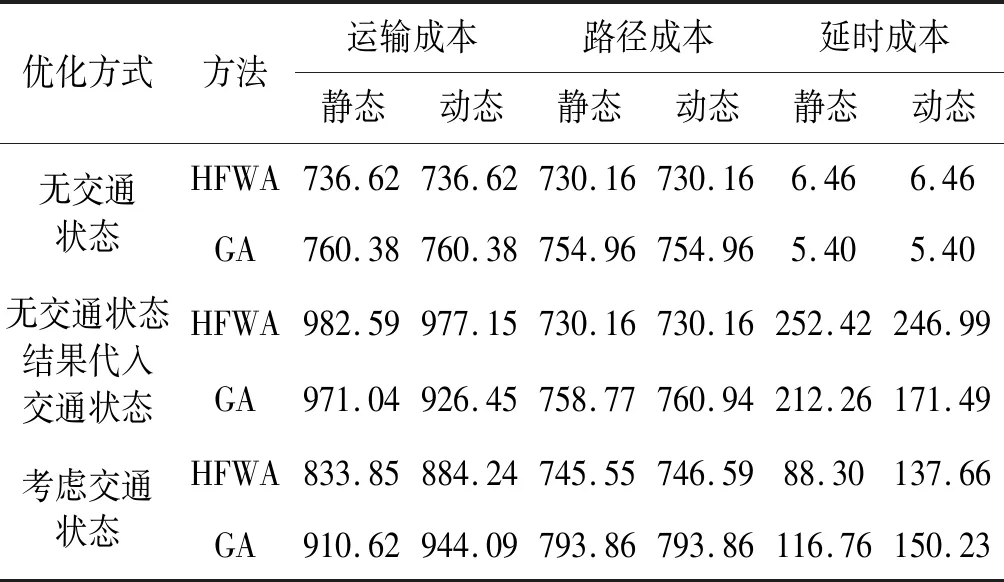
表4 实验计算结果

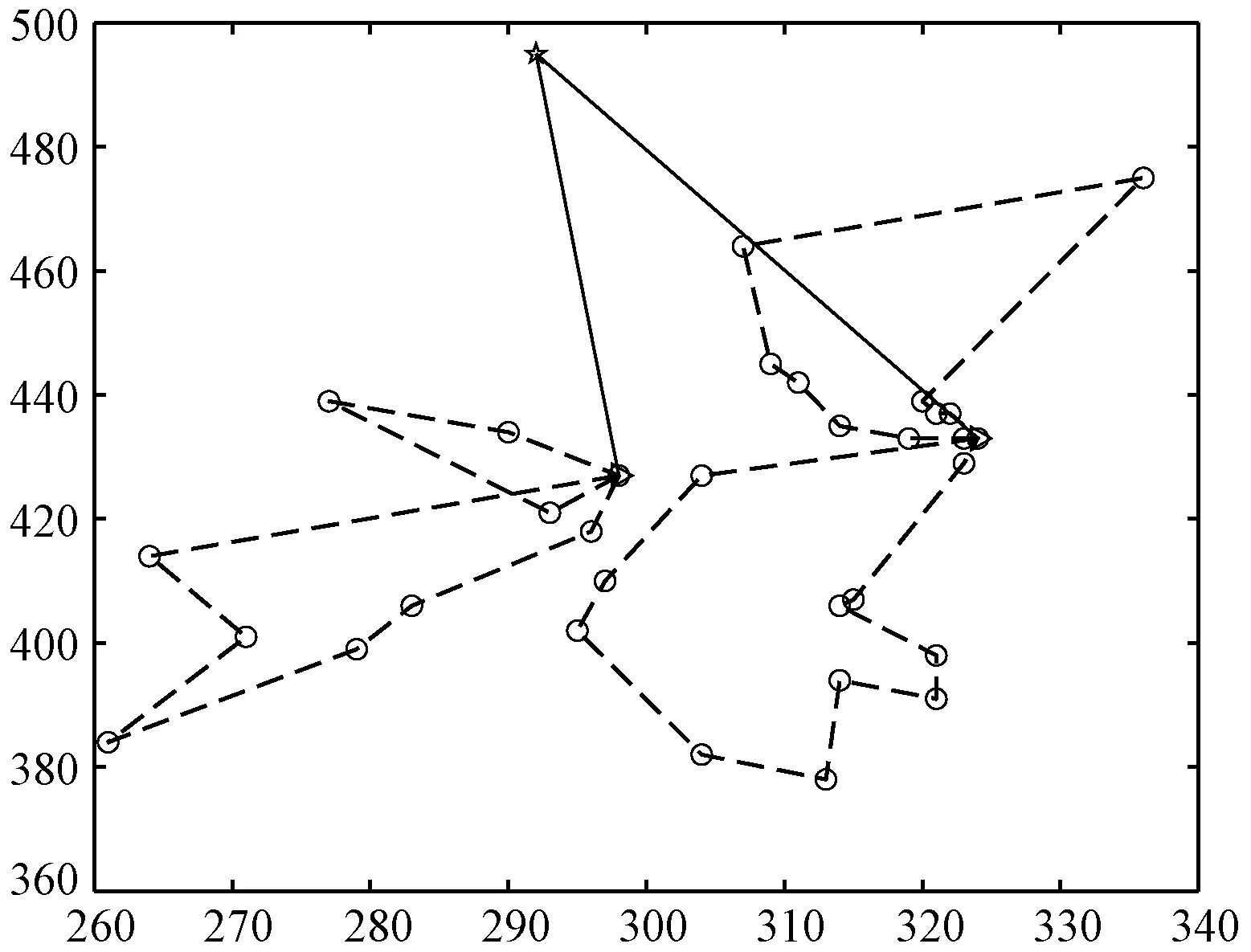
图6 HFWA不考虑交通状态的两级车辆路径

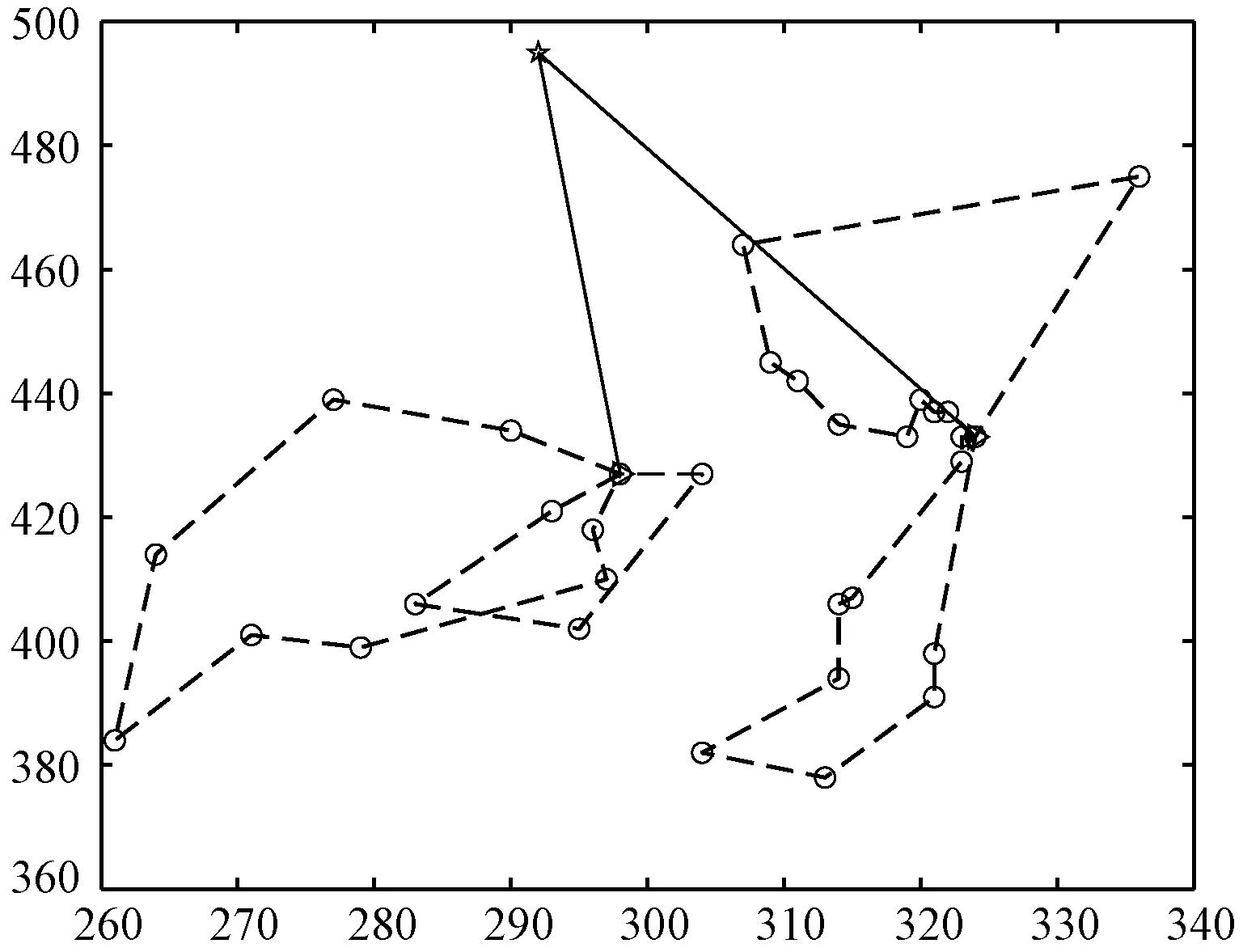
图7 HFWA考虑交通状态的两级车辆路径

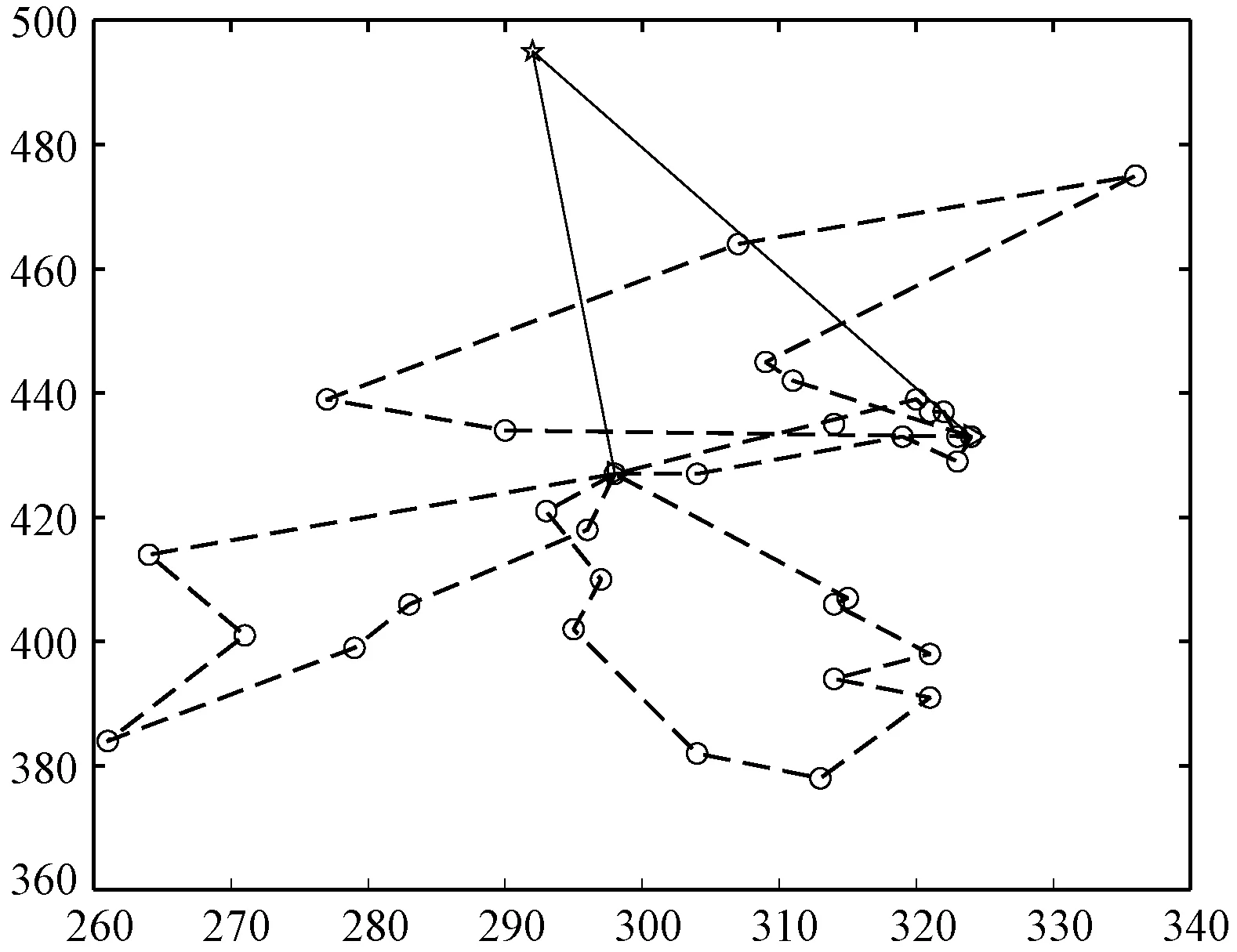
图8 GA不考虑交通状态的两级车辆路径

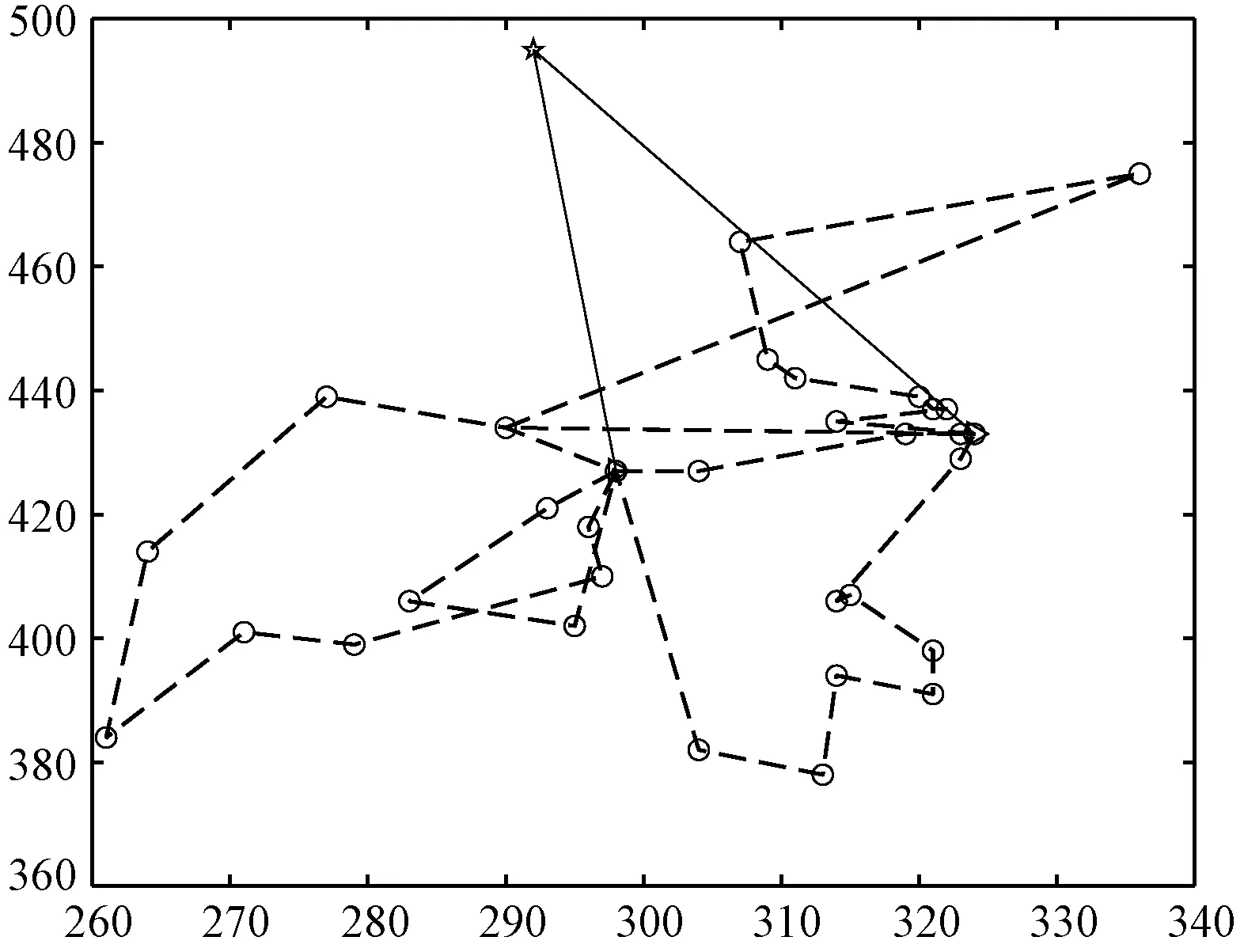
图9 GA考虑交通状态的两级车辆路径

从表4中可以得出,HFWA考虑交通状态下的优化结果,在静态交通下比不考虑交通状态条件优化结果代入到考虑交通状态后得到的总成本减少了17.8%,在动态交通状态下减少了10.5%,总成本平均减少了14.2%,说明了优化物流配送时考虑交通条件的必要性。而GA优化性能相较于HFWA相对较差。同时,考虑了交通状态在运输总成本、路径成本、延时成本相较于不考虑交通状态都有所增加,动态交通相较于静态交通,各个成本也有所变化,这是因为在物流配送过程中,交通状态变恶劣、不同道路交通状态在不同时刻不一致、物流节点间的路径选择策略缘故,使得车辆速度缓慢,车辆路径增加,配送时间延长,客户满意度下降。静态路径成本和动态路径成本不同则说明了在货物装车后的实际配送过程中,因交通状态的时刻变化,虽然车辆所服务的客户不再改变,但所行走的路线却根据动态交通状态做出了相应的变化以降低配送成本。从图6到图9也可以看出是否考虑交通对车辆路径也有所影响。在不考虑交通状态条件下,虽然对于延时配送成本,HFWA求解结果略高于GA求解结果,但是对于总成本以及路径成本,HFWA求解结果都远远低于GA求解结果。

由于车流量和道路施工情况在每个需求点之间不同,分析比较困难,而天气状态在一段时间内,各个需求点之间都相差有限。为了研究交通状态的影响因素对二级物流配送成本的影响,本文首先随机生成各个需求点之间的各个时刻的车流量指数和道路施工指数,将其固定不变,以天气状态指数为变量分析天气状态对配送成本、车辆行驶路径和延时惩罚成本情况的影响,分析计算结果如图10、图11和图12所示。

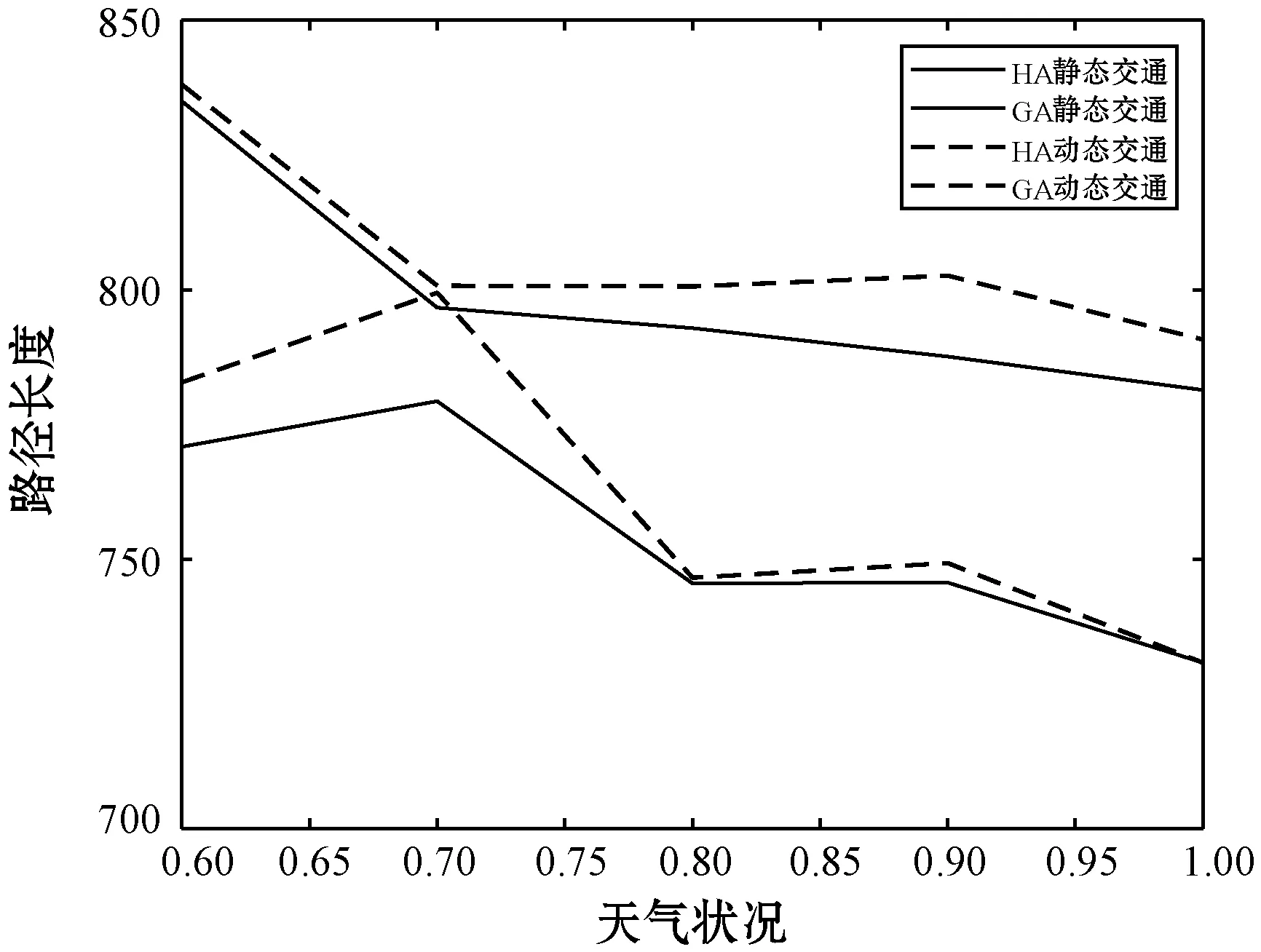
图11 天气情况对车辆行驶路径的影响

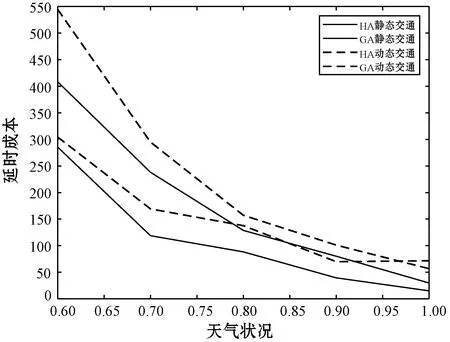
图12 天气情况对延时配送成本的影响

分析图10、图11、图12可知,在车流量指数和道路施工指数已知不变的情况下,运输总成本和延时配送成本随着天气的好转而降低,车辆行驶路径的长度总体上也随着天气的好转而缩短。在实际中,除了天气,考虑车流量以及道路施工等影响因素会更加符合实际物流配送,说明本文研究交通状态对运输成本的影响符合实际物流配送过程,可以在动态交通状态下有效降低物流配送成本,具有实际的应用价值,为动态二级物流配送路径优化提供了新思路。

5 结 语

本文考虑了车流量、道路施工和天气状态对交通状态的影响,将动态的交通状态和时间窗同时引入到两级物流配送中,建立了带时间窗的动态两级物流配送车辆路径优化数学模型,设计了求解该复杂问题的混合烟花算法。并利用混合烟花算法和遗传算法计算2e-VRP标准算例,并与现有文献所提算法对比说明本文算法的可行性和高效性。在标准算例的基础上构造新的具有时间窗的实验数据,然后用两种算法计算带时间窗的动态两级物流配送车辆路径规划数学模型,结果表明混合烟花算法收敛速度快,迭代次数少,且求解质量和求解效率均优于遗传算法。最后,分析了交通状态的影响因素对车辆路径以及配送成本的影响;证明了在实际物流配送车辆路径规划过程中,考虑动态交通的优化结果更加符合实际物流配送过程,具有实际应用价值,且算法设计合理,为求解动态交通的两级物流配送车辆路径问题提供了新方法。

本文仅仅考虑了一部分影响交通状态的因素,在实际的物流配送过程中,还存在车辆限行政策、客户需求的动态变化等因素,这值得在后续的研究中进一步探讨。