三维复杂断层建模关键算法研究

侯晓琳 强伟帆

(北京大学地球与空间科学学院 北京 100871)

0 引 言

断层是一种重要的地质构造,是控制油田剩余油分布的主要因素,也有可能是油气渗流的通道,断层模型的准确性直接影响油藏数值模拟的结果[1-2]。断层建模是地质结构建模和属性建模的基础,由断层、地层等地质界面封闭包围成地质实体,三维断层模型的准确性影响地质结构建模和属性建模质量[3-5]。断层模型可以描述断层构造的几何形态,断层之间的接触关系,可以描述断层之间的关联关系,构建断层模型的几何拓扑关系实现几何元素之间的快速索引能大大提高断层建模处理速度[6-7]。

断层建模主要包括生成断层网格模型和描述断层接触关系。基于断层点数据能生成并优化三维断层网格化模型,真实反映断层展布情况。在复杂断层网中,当断层倾向不一致时可能出现断层交叉、重叠、截断等情况,因此会形成Y型[8]、X型[9]、半Y型、半λ型断层,构建这些断层模型过程复杂[10]。目前复杂断层建模方法主要是基于初始化断层面网格模型,采用人工交互的方式描述断层接触关系,生成复杂断层网格化模型,建模效率较低,并且在应用复杂断层模型建立三维地质体模型时受到一定条件的限制[11-12]。

为改进现有复杂断层建模存在的问题,提出一种自动判断断层接触关系的算法,基于先验地质断层类型,自动生成复杂断层模型,减少了人工交互工作量,保留了几何拓扑关系一致性特征,提高了断层建模和三维地质建模效率。

1 三维复杂断层建模

国内外学者对三维地质建模研究较多[13],三维地质结构建模方法主要包括钻孔建模、基于三棱柱建模、结构化网格建模、隐函数建模等[14-16]。根据不同的三维地质建模思路,采用不同的断层建模方法,但是描述复杂断层形态存在一定难度。比如,基于Pillar网格的断层建模无法准确生成复杂断层模型[17]。因此,三维复杂断层建模研究具有意义和应用价值。

三维复杂断层建模流程主要包括断层网格模型生成和复杂断层接触关系描述两部分(图1)。基于断层点集数据构建三维断层三角化网格模型,保证几何拓扑关系一致性,作为初始化断层面模型。进而控制生成的断层面网格模型质量,优化并加密网格模型。在构建简单断层网格模型基础上,判断断层接触关系,生成断层接触关系描述,对具有接触关系的复杂断层进行优化和网格加密,改进网格质量。基于先验的地质知识断层类型,自动生成复杂断层网格模型,提高复杂断层建模效率。

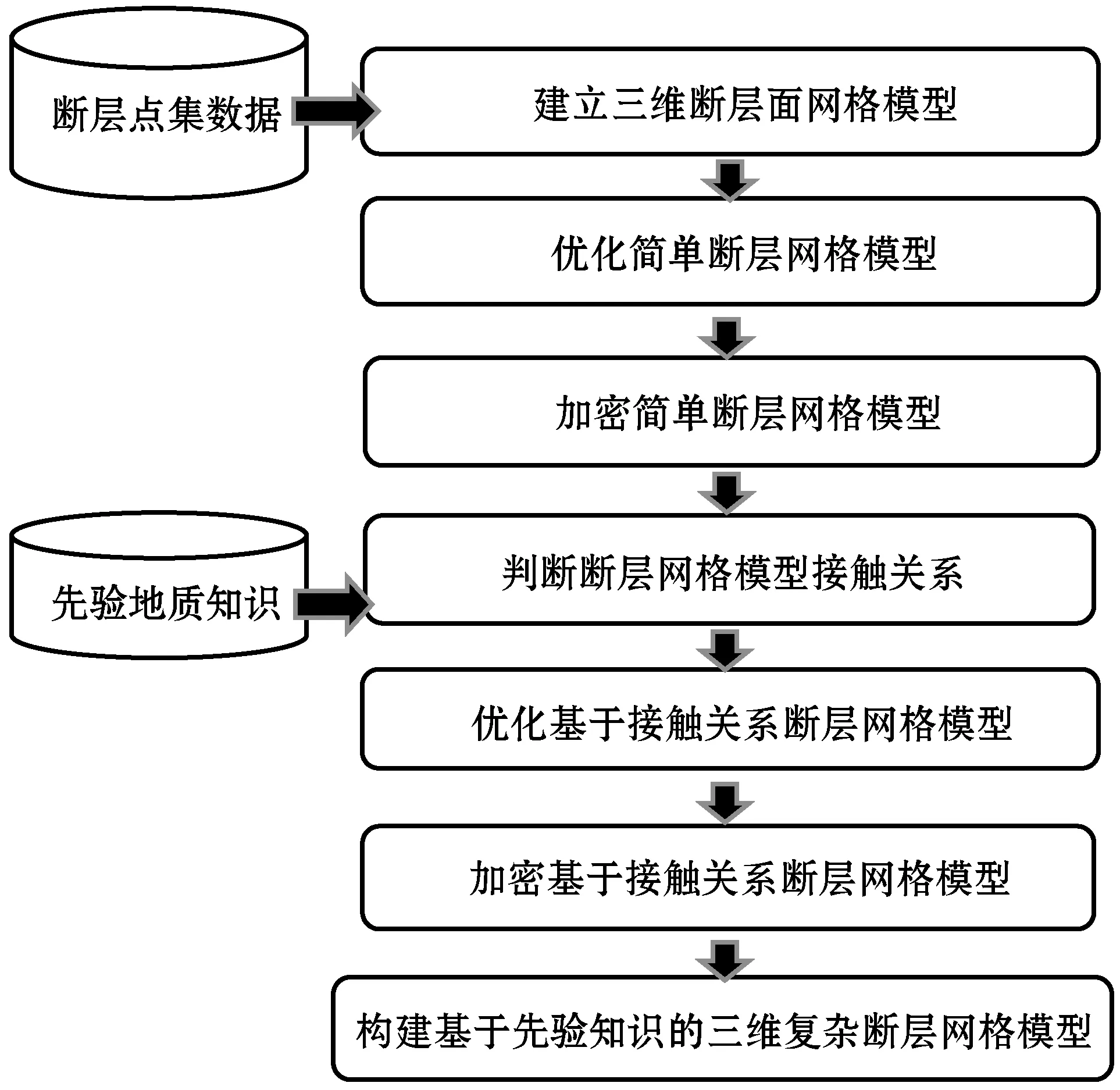
图1 三维复杂断层建模流程

2 三维断层三角化网格模型构建方法

2.1 三维断层三角化网格模型

构建断层三角化网格模型准确描述断层形态,结合映射法和二维三角化网格剖分算法[18-19],提出一种基于断层点集数据的三维断层三角化网格模型算法(图2)。

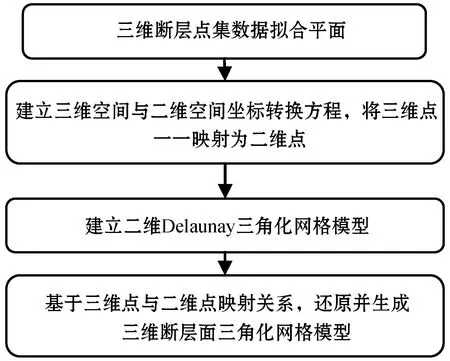
图2 基于断层点集数据构建三维断层面网格模型流程

首先基于三维断层点集的质心和拟合平面法向量计算断层点集的拟合平面。假设断层点集S包含n个三维点S={p1,p2,…,pn},点pi坐标为(xi,yi,zi)。计算点集S的质心点pc=(xc,yc,zc)。

(1)

计算点集S拟合三维平面P：w1x+w2y+w3z+w4=0的法向量,其中w表示待求参数。点集S中的所有点构成n×3矩阵An×3。

(2)

采用奇异值分解方法[20],将矩阵An×3分解为An×3=Un×nΣn×3V3×3,Un×n=[u1,u2,…,un],ui表示Un×n的列向量,对角矩阵Σn×3表示为：

(3)

式中：σ1、σ2、σ3为奇异值。V3×3=[v1,v2,v3],vi为V3×3列向量。最小奇异值σ3对应的列向量v3就是平面P的法向量,即v3=[w1,w2,w3]T。根据质心坐标,计算w4,w4=-w1xc-w2yc-w3zc。根据平面P方程和空间坐标转换将三维平面映射为二维平面。平面P上三维点pi=(xi,yi,zi)映射为二维点的转换矩阵M。

(4)

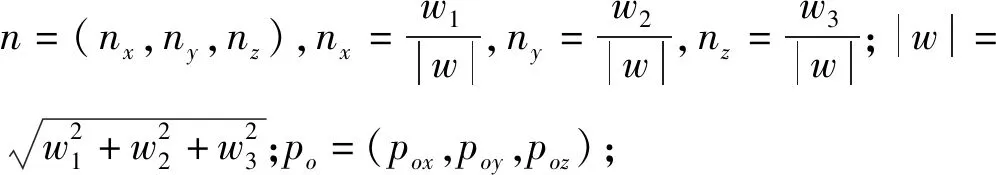
将三维断层面上的点一一映射到二维平面后,采用二维三角化剖分算法,建立二维Delaunay三角化网格模型T′,算法输入为三维点集P在二维平面上的映射点集P′,算法输出为三角化网格单元模型T。二维Delaunay三角化网格模型构建算法流程：

1) 计算二维平面上的点集P′的外包围框abcd,选取P′中的一点p0,p0与外包围框abcd构成三角形abp0、bcp0、cdp0、adp0,作为初始化三角化网格模型T′。

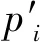
(a) (b)图3 加入点生成新三角形更新网格模型

4) 根据三维点与二维点的一一映射关系,构建并复原三维断层三角化网格模型T(图4)。

图4 基于映射关系构建三维断层三角化网格模型

基于断层点集数据,结合映射法和二维三角化网格剖分算法建立三维断层网格模型,准确描绘断层在三维空间中的展布情况,图5展示了基于断层点集生成的三维断层网格化模型。

2.2 三维断层面网格模型优化

基于三维断层网格化模型,维护几何拓扑关系,优化网格形态,进一步改进三维断层模型。三维断层网格模型优化主要包括畸形网格单元调整和网格加密。

几何拓扑关系模型是三维断层建模的基础,能够快速索引断层模型中的几何元素。图6是三维断层网格模型基本数据结构,维护几何拓扑关系,能够更加快速索引点、线、面数据,加快网格优化等计算速度。

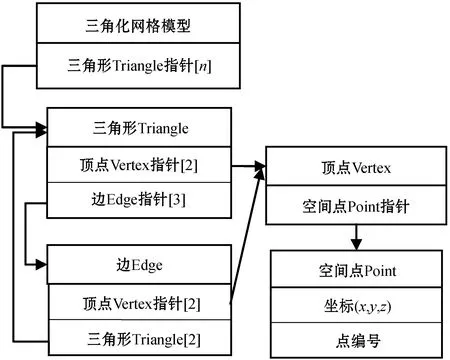
图6 三角化网格拓扑关系数据结构设计

基于断层点集数据生成的三维断层面网格模型可能存在畸形网格单元等问题,采用网格优化方法改进三维断层面网格模型形态。三角形单元网格质量评价指标有很多种,本文主要采用两种评价尺度：相邻三角形最小内角、三角形外接圆半径和最短边的比。通过增加数据点控制网格单元质量,优化网格单元形态。

1) 相邻三角形最小内角：基于网格几何拓扑关系采用局部调整方法优化两个相邻三角面结构形态。图7中,相邻三角形t(abc)和t(acd),计算两个三角形最小角,变换对角线bd,计算两个三角形t(abd)和t(bcd)最小角,基于最小角最大化原则选择最小角最大两个三角形加入网格模型。

图7 相邻三角形最小角最大化局部调整

最小角最大化局部调整算法输入包括断层三角形网格模型T,算法输出包括局部优化后的断层三角形网格模型T,算法流程：

(1) 依次遍历网格模型T中的每个三角形t,直至相邻三角形无须进行最小角最大化局部调整为止算法结束。否则,根据几何拓扑关系,快速查找三角形t共边邻接的三角形ts1、ts2、ts3。

(2) 依次判断三角形ts1、ts2、ts3与t的空间位置关系。假设tsi(bcd)和t(abc)共边bc,计算两个三角形的最小内角α,对换对角线ad,生成两个新三角形t(abd)和t(acd)。

(3) 计算三角形t(abd)所在三维平面S和点c在平面S上的投影点c′。若点c′在三角形t(abd)内(图8(a)),无法对换对角线ad,继续执行(1)。若点c′在三角形t(abd)外(图8(b)),继续执行(4)。

(a) (b)图8 相邻三角形对换对角线示意图

(4) 计算三角形t(abd)和t(acd)的最小内角α′,若α′>α,将三角形t(abd)和t(acd)加入到网格模型T,删除三角形tsi(bcd)和t(abc),更新几何拓扑关系,继续执行(1)。

2) 三角形t外接圆半径和最短边的比ρ：

(5)

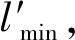
(1) 依次遍历三角化网格模型T中的每个三角形t,计算三角形t的外接圆与最短边比ρ,最长边长l和最短边长l′。

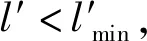
(3) 若ρ>ρmax,t为畸形网格单元,添加三角形t的最长边中点,构建新的三角形,更新几何拓扑关系。若三角形t最长边只属于三角形t,则生成两个新三角形;若三角形t最长边分属于两个不同的三角形,则生成四个新三角形,加入到网格模型T,删除畸形网格单元。继续执行(1)。

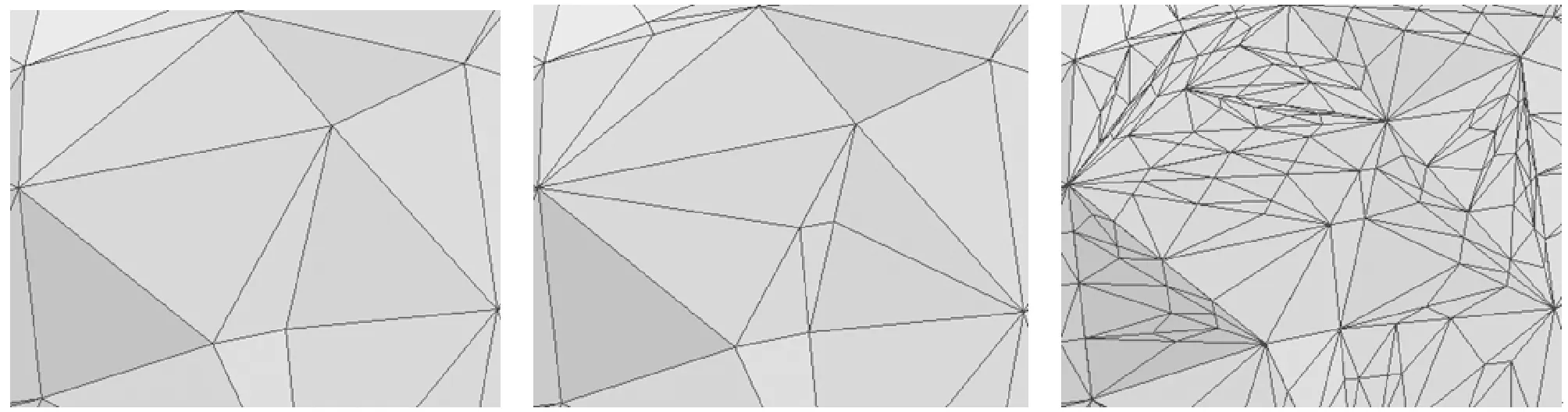
(a) (b) (c)图9 不同阈值断层局部网格优化加密效果

优化并加密后的断层网格模型作为复杂断层建模的基础模型,根据断层接触关系,进一步进行复杂断层建模。

3 复杂断层自动化建模方法

3.1 断层接触关系处理

断层接触关系判断和处理是复杂断层建模的基础,根据接触关系能够判断断层类型,结合先验地质知识,实现自动化复杂断层建模。

基于三维断层网格模型,建立三维空间栅格模型,判断三维断层网格模型T1和T2接触关系。假设。断层面T1和T2的外包围框为B1(a1b1c1d1-e1f1g1h1)和B2(a2b2c2d2-e2f2g2h2),表示为：

式中：xmin、xmax分别表示断层面T1中所有断层点最小x坐标和最大x坐标(图12)。栅格模型的大小是两个断层模型的并外包围框B：

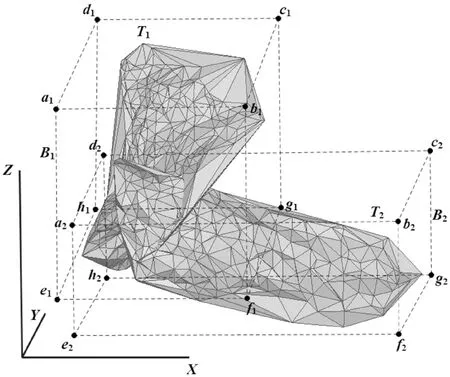
图12 两个断层模型T1和T2外包围框示意图

B=B1∪B2={xmin,xmax,ymin,ymax,zmin,zmax}

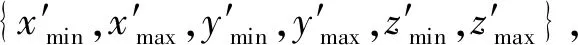
图13 三角形t所在栅格单元示意图

(6)

(7)

(8)

记录三角形t(abc)与所在栅格单元的对应关系,作为判断断层接触关系算法输入。断层接触关系判断方法简化为判断两个三角化网格模型相交关系。

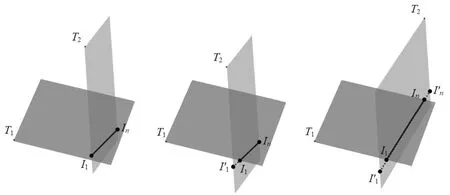
在某一个栅格单元cell(n,m,k)中的任意两个三角形t1∈T1和t2∈T2可能相交。遍历N×M×K个栅格模型中的所有栅格单元cell(n,m,k),若在同一个cell(n,m,k)中包含任意两个三角形t1(a1b1c1)∈T1和t2(a2b2c2)∈T2,进一步判断两个三角形是否相交并计算交点。判断任意两个三角形t1(a1b1c1)∈T1和t2(a2b2c2)∈T2相交关系和计算交点的算法输入包括三角形t1(a1b1c1)和t2(a2b2c2),算法输出包括是否相交判断结果,若相交,输出三角形相交交点。算法流程：

1) 计算三角形t1(a1b1c1)所在平面方程S1((x,y,z,1)T)：(w1,w2,w3,w4)·(x,y,z,1)T=0,将t2(a2b2c2)三点代入平面方程S1得到S1(a2)、S1(b2)、S1(c2)。若S1(a2)、S1(b2)、S1(c2)同为正值或者负值表示两个三角形不相交,算法结束;反之,执行2)。

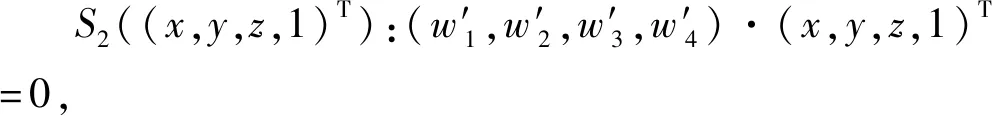
3) 三角形t1(a1b1c1)和t2(a2b2c2)相交,计算交点。如图14所示,依次计算t3-i(a3-ib3-ic3-i),i=1,2三边与三角形ti(aibici)交点。以边a3-ib3-i为例,若Si(a3-i)×Si(b3-i)<0,点a3-i、b3-i在平面Si两侧,计算线段a3-ib3-i与平面Si的交点I。若交点I在三角形ti(aibici)内,则交点I就是两个三角面t1和t2的交点,记录两个相交三角形以及t3-i(a3-ib3-ic3-i)的一边a3-ib3-i。保存三角形与另一三角形边的相交关系。

图14 两个相交三角形位置关系及交点示意图

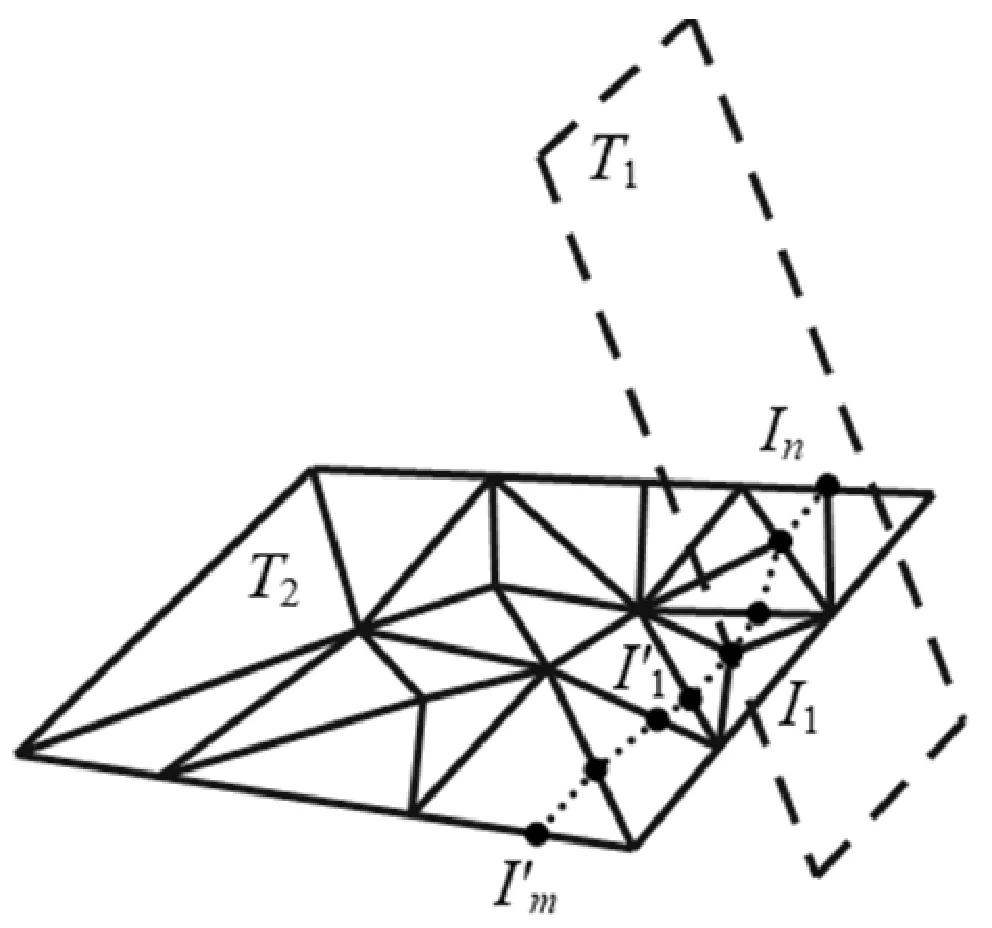
在计算出两个断层网格模型所有交点的基础上,采用ear clipping算法基于交点交线分割相交三角形,保留交点、交线的同时保证几何拓扑关系一致性。ear clipping算法流程主要包括构建三角形闭合多边形和三角形分割算法两个部分[21]。断层网格模型中一个三角形ti(aibici)与另一个断层模型中的三角形相交,假设交点集合I={I1,I2,…},首先需要基于交点构建三角形ti(aibici)的闭合多边形。三角形ti(aibici)闭合多边形Po构建算法输入包括三角形ti(aibici)和ti(aibici)上交点集合I,算法输出为三角形ti(aibici)闭合多边形Po。算法流程：

1) 基于坐标轴对交点集合I进行排序,假设排序后I={I1,I2,…,In},那么交线线段集合为L={I1I2,I2I3,…,In-1In}。

2) 计算三角形ti(aibici)三边与交线线段L构造闭合多边形Po。基于交线线段构建闭合内环为I内={I1,I2,…,In,In-1,…,I3,I2}。基于三角形三边构建闭合外环。若任意交点Ii位于三角形边上,将交点Ii加入到闭合外环。根据三角形ti(aibici)与交线线段的位置关系不同,三角形ti(aibici)闭合多边形Po构建方法不同,分成以下三种情况：

(1) 交线两端与均在三角形ti边上(图15(a))：闭合外环I外={ci,I1,ai,bi,In},基于连接点I1连接闭合外环和闭合内环,构建闭合多边形Po={ci,I1,I2,…,In,In-1,…,I2,I1,ai,bi,In}。

(2) 交线一端在三角形ti一边上,其余交点在三角形内(图15(b))：闭合外环I外={ci,I1,ai,bi},基于连接点I1连接闭合外环和闭合内环,构建闭合多边形Po={ci,I1,I2,…,In,In-1,…,I2,I1,ai,bi}。

(3) 交线点均在三角形ti内(图15(c))：闭合外环I外={ci,ai,bi},建立内环与外环连接线段aiI1,基于连接线段,闭合外环和闭合内环构建闭合多边形Po={ci,ai,I1,I2,…,In,In-1,…,I2,I1,ai,bi,In}。

基于三角形ti顶点与交点构成闭合多边形Po,依次遍历并删除闭合多边形上的点生成新三角形,直至分割生成所有的新三角形。基于闭合多边形Po分割三角形算法输入闭合多边形Po,算法输出分割后的新三角形。算法流程：

1) 若ti(aibici)的闭合多边形Po中有且仅有三个点pi-1、pi、pi+1,则pi-1、pi、pi+1构成新三角形;否则,执行2)。

2) 遍历ti(aibici)的闭合多边形Po中一点pi∈P其前继点表示为pi-1∈P,后继点为pi+1∈P。若pi-1、pi、pi+1共线,无法构成三角形,继续遍历Po中下一点,执行2);否则,执行3)。

3) 若pi-1、pi、pi+1不共线,则pi-1、pi、pi+1可以构成三角形。判断Po中其他点是否在三角形t(pi-1pipi+1)内,若其他点在三角形内,pi-1、pi、pi+1无法构成新三角形,继续执行2);反之,pi-1、pi、pi+1构成新三角形t(pi-1pipi+1),在闭合多边形Po中删除当前点pi。

(a) (b)图16 ear clipping算法分割三角形

图17展示了分属于不同断层模型的两个相交三角形,采用ear clipping算法分割新三角形结果。图18展示了两个三角化网格模型相交关系和相交处理结果。图19展示了基于两个断层模型接触关系处理后的网格模型。

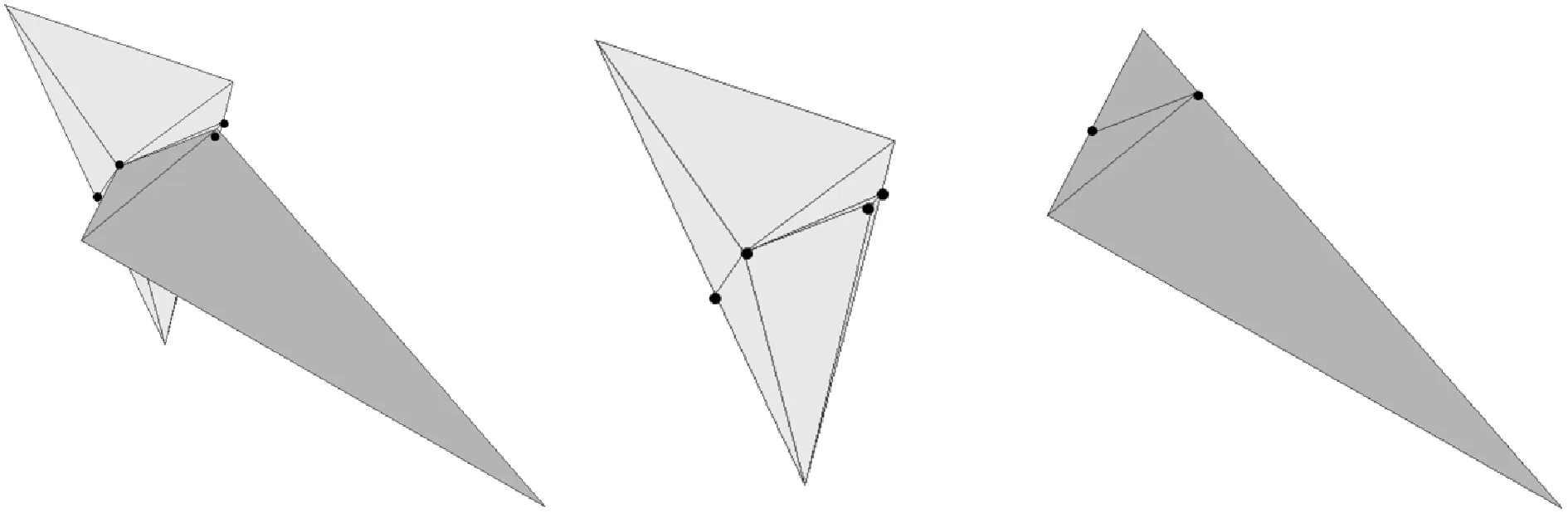
图17 采用ear clipping算法分割两个相交三角形结果示意图

图18 两个三角化网格模型相交处理示意图

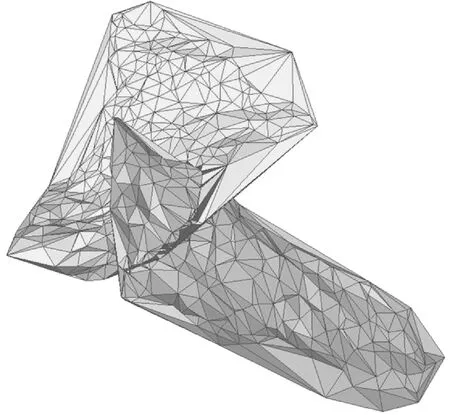
图19 基于两个断层模型接触关系处理后的网格模型

3.2 复杂断层网格模型优化

采用相交线段描述断层网格模型的接触关系,构建复杂断层网格模型,在交线约束基础上,优化三角化网格模型形态,加密网格模型。

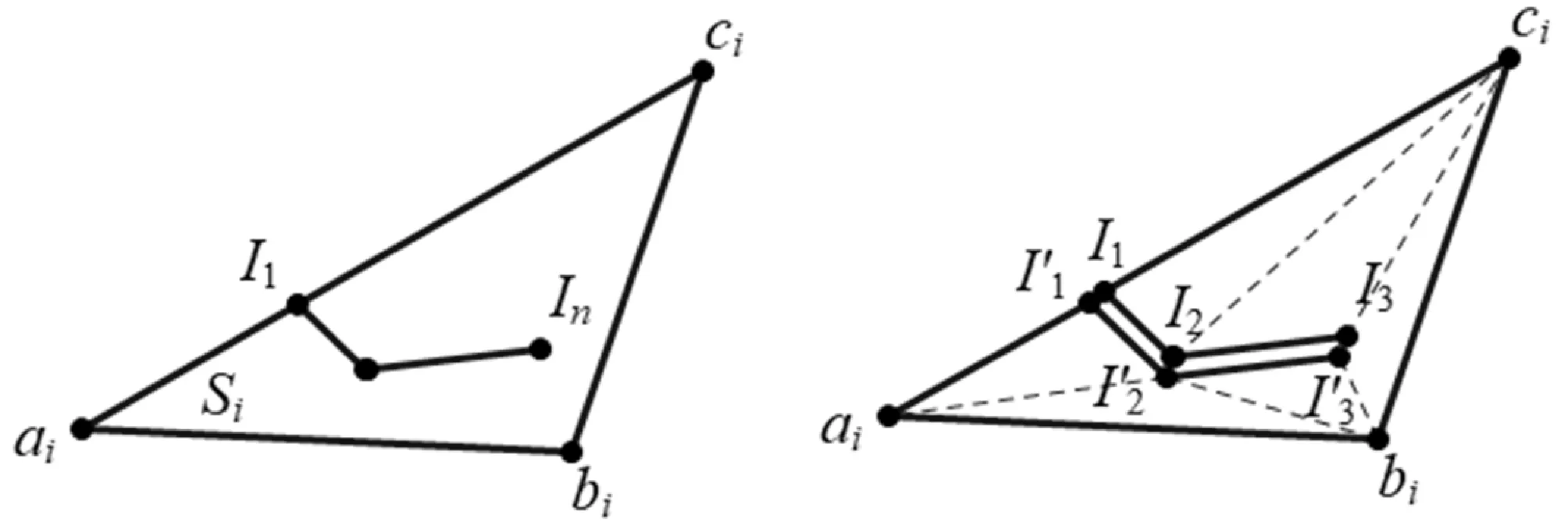
优先优化以交线为边或交点为顶点的三角形网格单元形态,准确描述断层模型接触关系。在任意一个相交三角形t(abc)中,遍历所有分割生成的新三角形ti(aibici)的每一条边e,若边e不属于交线线段L且共属于两个不同三角形,依据最小角最大原则判定是否对换对角线生成并更新新三角形。图20中,保留交线线段I1I2、I2I3、I3I4,对换对角线I1b、I1I3,生成新三角形t(aI1I2)、t(abI2)、t(I1I2c)、t(I2I3c),删除原有三角形t(I1ab)、t(bI1I2)、t(I1I2I3)、t(I1I3c)。

(a)

图21展示了基于相交线段约束,相交网格模型优化前、后的接触关系的不同描述结果。

(a)

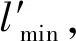
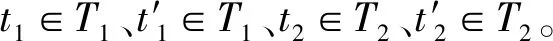
2) 依次遍历三角化网格模型Ti中的每个三角形t,计算三角形t的外接圆与最短边比ρ,最长边长l和最短边长l′。

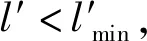
4) 若ρ>ρmax,添加三角形t的最长边中点m,若三角形t的最长边不属于相交线段,构建新三角形,更新几何拓扑关系。若三角形t的最长边属于相交线段e(IiIi+1),执行5)。

图22展示了两个相交的三角化网格模型经过优化、加密后更新的网格模型。图23展示了具有接触关系的复杂断层网格模型优化加密后的可视化效果。

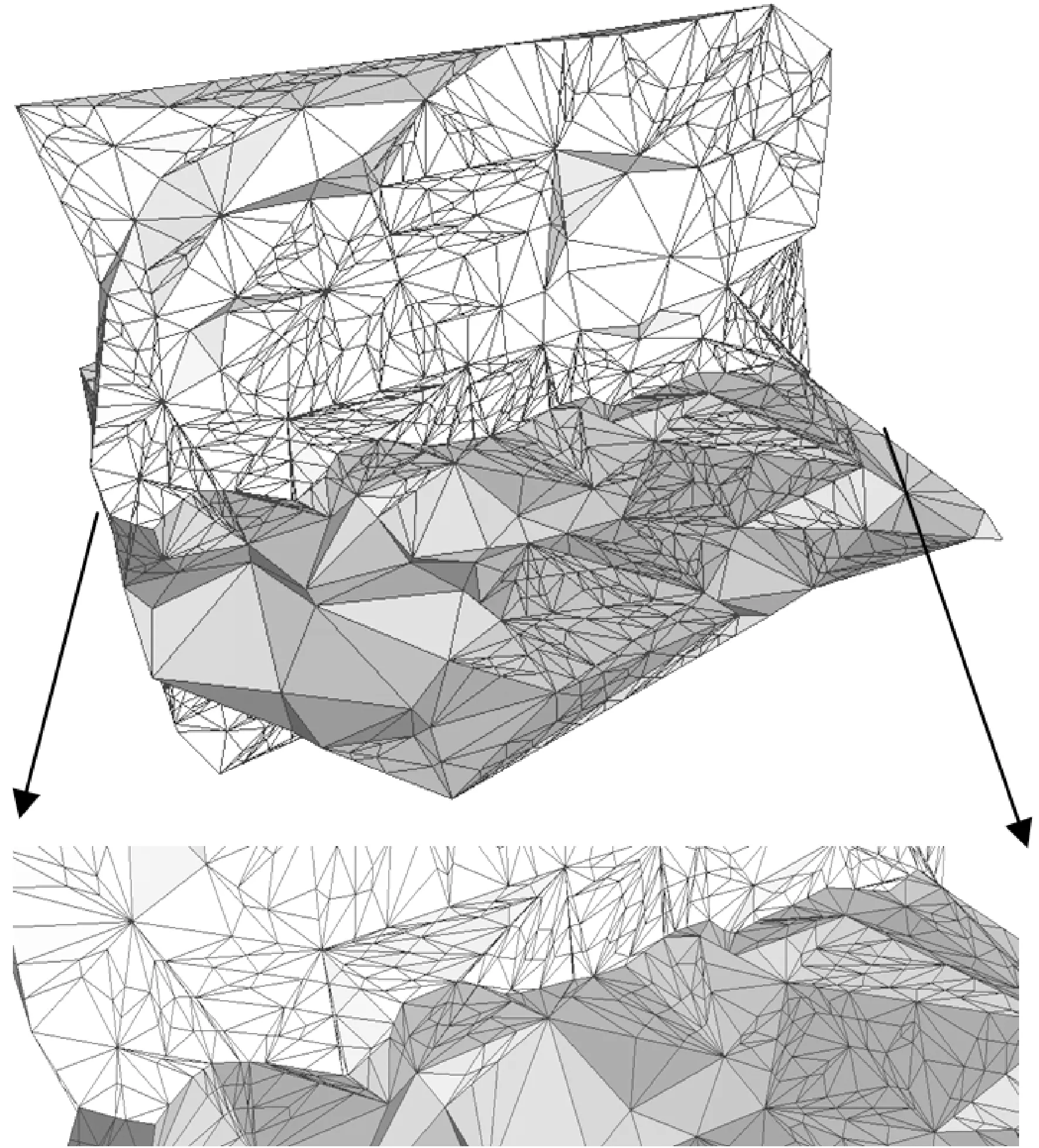
图22 两个相交三角化网格模型优化加密后的网格模型

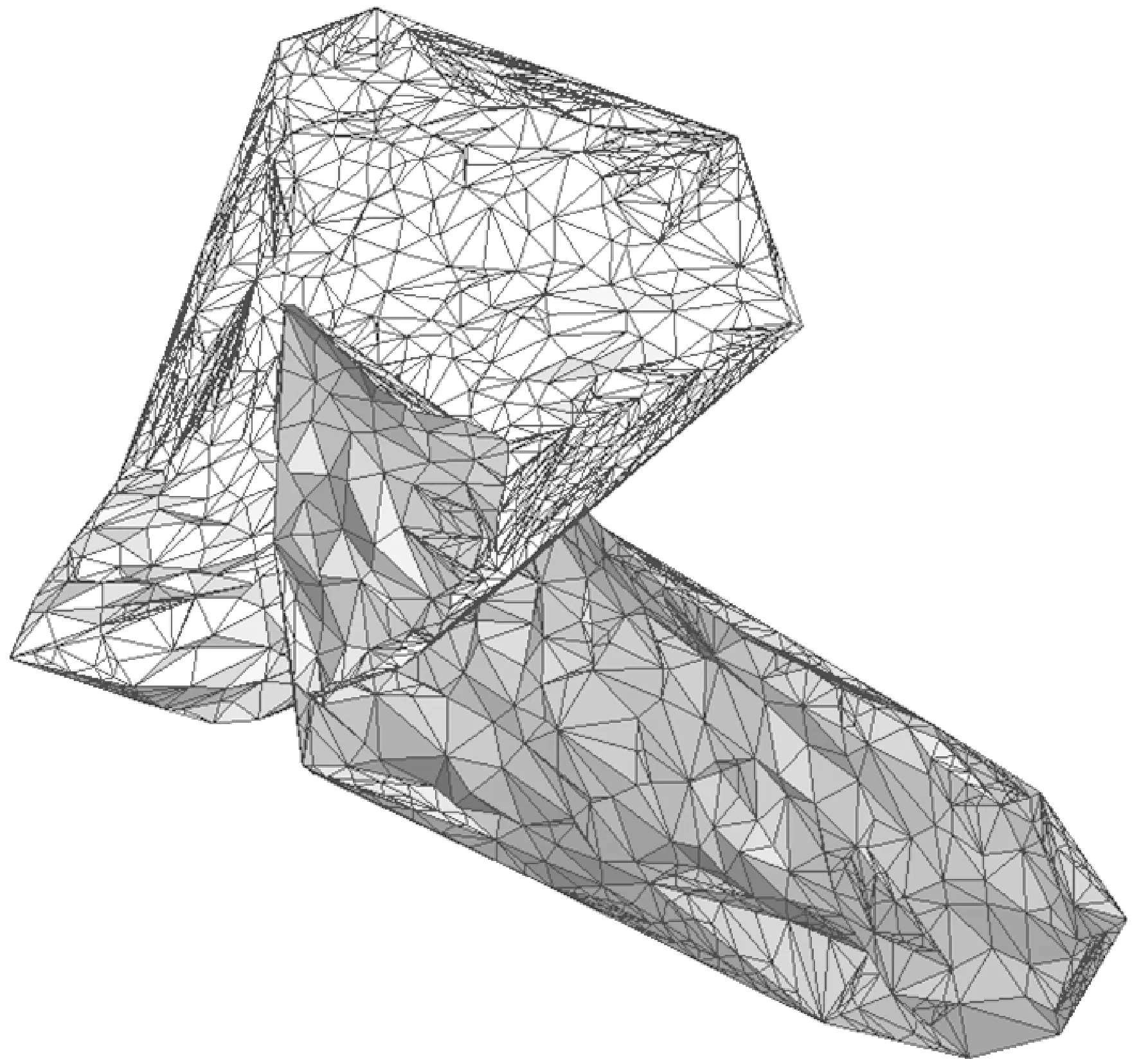
图23 具有接触关系断层面网格模型优化加密结果示意图

3.3 基于地质先验知识生成复杂断层模型

在现有地质断层先验知识的基础上,根据断层和分支断层关系,基于三维断层网格模型接触关系,自动生成三维复杂断层网格模型。假设两个相交三维断层网格模型T1、T2,基于先验知识已知T1为主断层,T2为分支断层,主断层模型完全截断分支断层模型,基于两个断层网格T1、T2构建复杂断层网格模型,描绘复杂断层展布情况。首先基于主断层T1、分支断层T2,计算并生成分支断层T2的分割线段,分割线段将分支断层T2截断成两个子网格模型,其中之一面积较大网格模型表示分支断层T2实际展布情况。在分支断层没有被主断层完全截断的情况下,需基于T1、T2的相交线段L={I1I2,I2I3,…,In-1In}计算相交线段的延长线段形成分割线段。根据不同的接触关系,分割线段主要包括以下三种情况：

1)T1、T2的相交线段L就是截断T2的分割线段(图24(a))。

(a) (b) (c)图24 不同接触关系的主断层与分支断层

2)T1、T2的相交线段L及一端延长线组成分割线段截断T2(图24(b))。

3)T1、T2的相交线段L及两端延长线组成分割线段截断T2(图24(c))。

基于图24所示的不同接触关系的主断层截断分支断层,构成复杂断层模型(图25)。

(a) (b) (c)图25 不同接触关系的主断层截断分支断层示意图

(a)

根据地质断层先验知识,判断是否需要生成断层T2截断线段,截断T2断层,生成复杂断层模型。若需要截断T2断层,采用先进先出队列,遍历三角形的邻接关系,当三角形的一边属于截断线段时,与其共边三角形属于截断后的两个不同子网格模型,反之,则与其共边三角形属于同一个网格模型,最后断层T2被截断成两个子网格模型。针对于Y型断层来说,删除截断后网格面积较小的子网格模型,构成Y型断层网格模型。

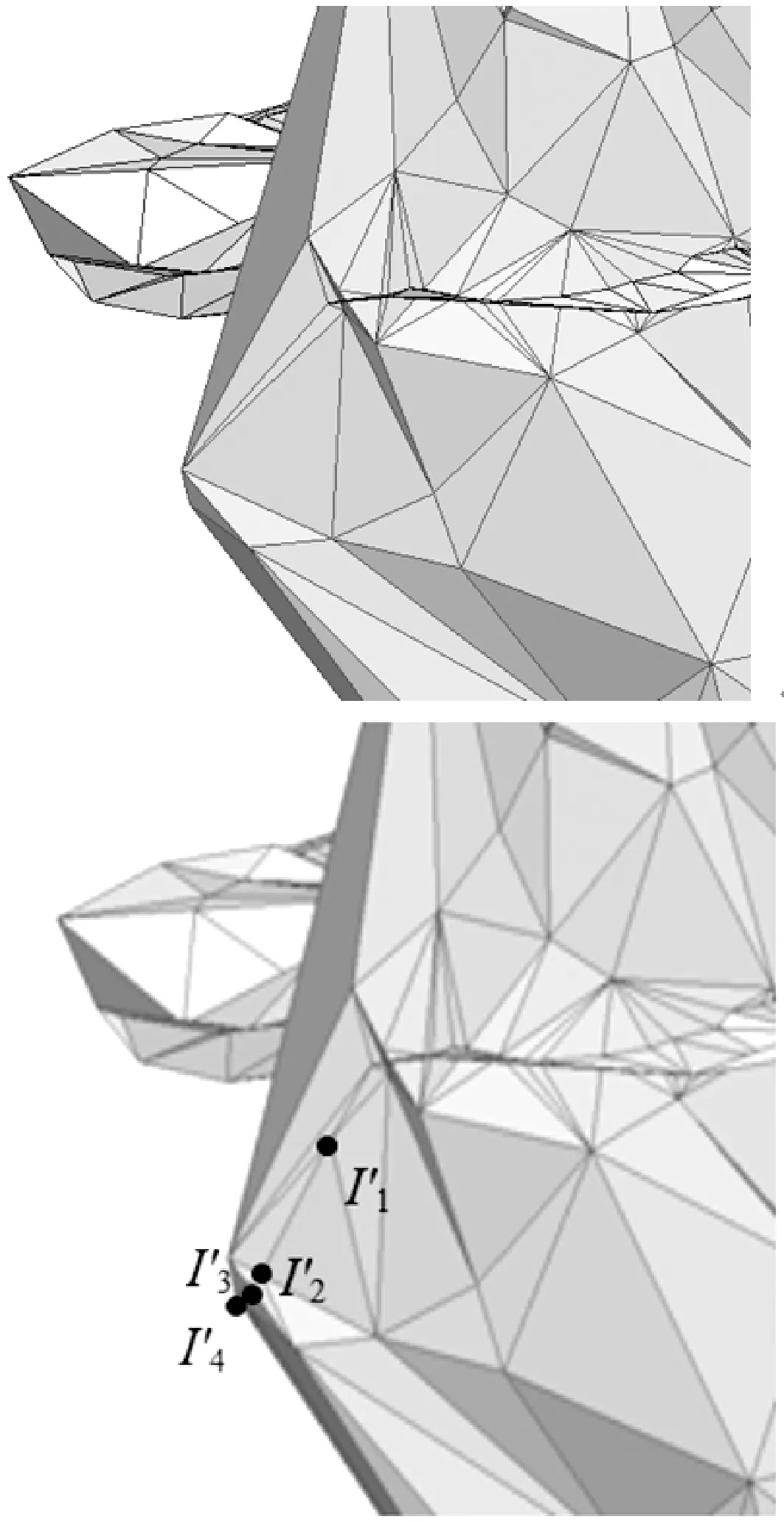
图27 分支断层模型的截断线段计算过程

(a)

4 结 语

断层建模是三维地质建模的基础,基于断层点集数据构建三维断层网格化模型,能够真实反映断层展布情况。断层之间的接触关系复杂,采用人工交互方法构建复杂断层模型,工作量较大,建模时间较长,本文提出一种基于断层点集数据,根据已有的地质断层类型先验知识,自动构建复杂断层网格模型的方法,准确还原复杂断层构造形态,减少人工交互工作量,提高三维断层建模效率。