有理函数积分相关知识的补充
刘 烁, 王瑞星, 徐清华, 张 惠, 吴克坚
(空军军医大学 基础医学院,陕西 西安 710032)
0 引言
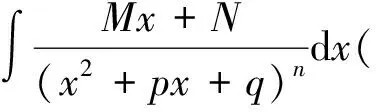
1 有理函数有关概念的补充
所谓有理函数,是指两个多项式的商
当n 1)若Q(x)中有形如(x-a)k的因子,则其对应部分分式之和为 其中A1,A2,…,Ak为待定系数; 2)若Q(x)中有形如(x2+px+q)l(p2-4q<0)的因子,则其对应部分分式之和为 其中M1,N1,M2,N2,…,Ml,Nl为待定系数[1]。 待定系数法是确定部分分式中待定系数的一般方法,教材中例题即采用此方法,但除了这种方法之外,还有几种行之有效的方法,在此加以补充。 1)赋值法。当有理真分式分母含有形如x-a或x2+px+q(p2-4q<0)的因子时,可对通分后所得等式中的x赋值,使得等式中一些项为0,以简化运算。 x+2=A(x2+x+1)+(Bx+D)(2x+1), (1) 为了求出系数B,D,可令x2+x+1=0,则右端第一项为0,从而有 (x+2)|x2+x+1=0=(Bx+D)(2x+1)|x2+x+1=0, 2)极限法。当分母只有一次因子时,也可用取极限的方法求出待定系数。 如 (2) 因此B=-1,D=0。 3)求导法。当分母含有因子(x-a)k、(x2+px+q)l(k,l为大于1的正整数)时,可通过求导法确定系数。如 A3可通过赋值法得到,即等式两边同乘以(x+1)3,再令x=-1,则可得 B2,D2也可通过赋值法得到,即等式两边同乘以(x2+x+1)2,再令x2+x+1=0,此处仍然将x2+x+1作为整体对待,则可得 (x2-1)|x2+x+1=0=-x-2, 因此,B2=-1,D2=-2。 A1,A2可通过求导得到,等式两边同乘以(x+1)3, ((B1x+D1)(2x+1)+B2)|x2+x+1=0=(2B1x2+(2D1+B1)x+D1+B2)|x2+x+1=0= (2B1(x2+x)+(2D1-B1)x+D1+B2)|x2+x+1=0=(2D1-B1)x+D1+B2-2B1, 因此有 解得B1=-3,D1=-3。 4)奥斯特洛格拉得斯基方法。所谓奥斯特洛格拉茨基(OSTROGRADSKY M V)方法,就是利用代数方法将有理真分式化为另一个真分式的导数和几个简单真分式(分母次数达到最低状态)之和[2],使得每一项的积分都易计算,即 其中P(x),k,l,a,p,q已知,P(x)的次数不超过分母次数k+2l-1,P1(x)为k+2l-4次待定多项式函数,b,c,d为待定系数。 右端导数按求导法则求出后再通分,等式两端分子同幂次项系数相等,解方程组可求出待定系数。 1=(x3+1)(2A1x+A2)-3x2(A1x2+A2x+A3)+A4(x2-x+1)(x3+1)+(A5x+A6)(x+1)(x3+1), 比较同次幂系数可解得 所以 所以 注意,当分母的因子幂次较高时,待定系数法确定系数比较繁琐,不适合使用。 1)Matlab代码。 syms x y=(x+2)/((x+1)^3*(x^2+x+1)^2) int(y) 2)Python代码。 from sympy import * x=symbols(′x′) y=(x+2)/(((x+1)**3)*(x**2+x+1)**2) print(integrate(y,x) ) 1)Matlab代码。 syms x y=(x+2)/((x+1)^3*(x^2+x+1)^2) int(y,0,1) 2)Python代码。 from sympy import * x=symbols(′x′) y=(x+2)/(((x+1)**3)*(x**2+x+1)**2) print(integrate(y,(x,0,1))) 有理函数的积分是很重要的一个知识点,也是高等数学的一个难点内容。 在教学实践中,学生对这一部分内容的掌握情况不是很好,主要原因还是掌握的方法不多,一旦遇到稍复杂的形式便无所适从,为此,基于教材对这一部分内容进行适当的补充,为读者提供更多的方法,可让读者有更多的选择余地,从而更好地掌握求有理函数积分的方法[3-6]。当然,每一种方法都有一定的适用范围,应根据被积函数的特点选择恰当的方法,或者几种方法结合起来使用。2 化有理函数为部分分式之和的方法补充
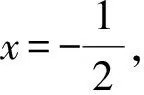
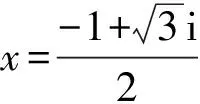
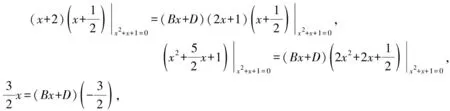
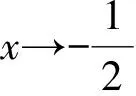
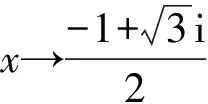
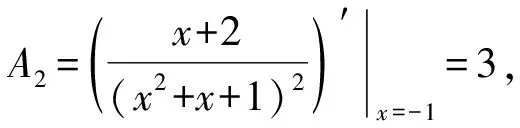
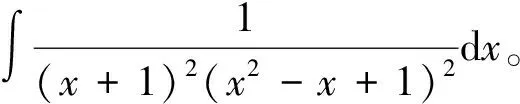
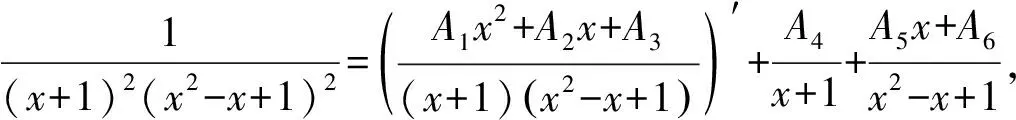
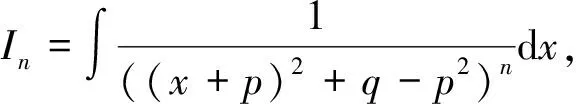
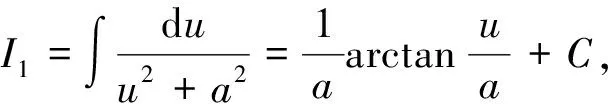
4 利用数学软件计算有理函数的积分
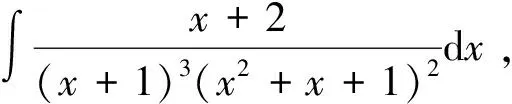
5 结语

