面向新型四自由度3T1R并联机器人的动力学分析和近似建模方法

贾 锶,王桂荣,陈思鲁,胡 华,张 驰,杨桂林

(1.中国计量大学 机电工程学院,浙江 杭州 310018;2.中国科学院 宁波材料技术与工程研究所,浙江 宁波 315201)

与传统的串联机器人相比,并联机器人是一类新型机构,具有刚度较强、动态性较好、惯性较小、承载能力较高、累积误差小等优点[1]。空间四自由度的并联机构可广泛应用于分拣、包装、码垛、装配、3D打印技术[2-3]等操作中。

目前关于并联机器人动力学建模的方法很多,如崔敏其[4]用拉格朗日公式法对SCARA机器人的动力学模型进行了详细推导,刘国军[5]利用凯恩法对三自由度Delta并联机器人建立了动力学反解模型,姜园等[6]基于牛顿-欧拉方法对3-RRRT并联机器人进行了系统动力学模型构建,徐灵敏等[7]以几何代数为工具结合虚功原理法确定并联机器人驱动力或力矩的几何表达式。其中拉格朗日函数方法较为简单、紧凑,不需要求解内作用力,然而由于空间并联结构复杂、耦合度高,而且随着关节数和自由度的增加,使用拉格朗日函数方法计算得到的结果越来越复杂,运算量急剧增加,无法满足实时控制的需要。

能实现高效计算的逆动力学模型是并联机器人在高速高精应用中实现实时控制的关键性因素[8],本文以构型为4PPa-2PaR[9]的四自由度三平移一旋转(three-degree-of-freedom translations and one-degree-of-freedom rotation,3T1R)并联机器人为探究对象,首先分析该机器人机械构型及其运动学模型,并在此基础上,采用拉格朗日函数方法建立其动力学模型;其次,基于该机器人构型的几何对称性、构件理想化、杆件质量小等特性,对该模型进行近似化简;最后,对该机器人在实际工况下的轨迹进行跟踪仿真实验,验证了近似建模方法的可行性,从而为该机器人的控制和优化提供依据。

1 机械结构描述

本文所研究的四自由度3T1R并联机器人机械结构如图1。图1中,机器人结构由定平台、动平台、4个磁悬浮直线电机、4组主动臂、2组从动臂、2个主从动臂连接件组成。

图1 四自由度3T1R并联机器人Figure 1 4-DOF 3T1R parallel robot

本机械系统中,同侧的2个电机共用一个定子[10],2个定子平行等高地固定在定平台上,主动臂、从动臂皆为平行四杆机构,2个主从动臂连接件以转动副分别连接对应侧的2个主动臂和1个从动臂,主动臂组与电机动子以转动副连接,从动臂组以转动副与动平台相连。动平台的位置和姿态由4个磁悬浮电机的位置决定。

2 动力学分析

本文所研究的四自由度3T1R并联机器人结构对称,而且只需要求得直线电机的驱动力,即建立机器人的逆动力学模型,而不需要求解相互作用的内作用力[11],故本文选用较为简单紧凑的拉格朗日函数方法来建立机器人的动力学方程,用拉格朗日函数方法进行分析时,只需要考虑系统的能量——包括系统的动能和势能即可。

2.1 等效模型

为了便于建模,假设有以下条件:把全部对象视作刚体,把平行四杆机构简化为连杆,并按单个支链上的部件类型从电机到动平台进行标号,建立忽略小偏置的连杆-质点等效抽象模型。

如图2,建立全局坐标系O-xyz,其原点O固定于电机M1所在导轨的左极限位置上。y轴方向定义为沿电机所在导轨向右方向,z轴方向定义为垂直于水平面竖直向上,x轴方向由右手定则确定。

图2 机器人等效模型图Figure 2 Equivalent model diagram of the robot

建立局部坐标系O′-x′y′z′,原点O′位于动平台质心处,z′轴方向与z轴方向相同,y′轴方向垂直于从动臂末端连线,指向y轴正方向,x′轴方向由右手定则确定。

相关几何参数定义如下:l2、l4、l5为部件2、4、5的长度,l2c、l4c、l5c为部件2、4、5的质心到与上一部件连接点的长度,L为两平行导轨间距。

2.2 位置与速度

电机的质心的位置分别为

(1)

式(1)中,y1、y2、y3、y4分别为电机M1、M2、M3、M4的质心在Oy方向上的坐标值,m。

与电机M1、M3相连的主动臂与平面xOy形成的锐角分别为主动角α1和α2,与电机M2、M4相连的主动臂与平面xOy形成的锐角在量值上分别与α1和α2相等。α1和α2可由电机的y轴坐标计算如式(2):

(2)

令sαi=sinαi,cαi=cosαi,则主动臂的质心的位置可被分别表示如式(3):

(3)

主从动臂间连接件的质心位置分别为

(4)

从动臂与平面yOz成的锐角分别为从动角β1和β2,令sβi=sinβi,cβi=cosβi,从动角可由x轴和z轴上的约束[12],即式(5)计算:

(5)

式(5)中,θ为动平台绕z′轴转动的角度,即O′x′轴与Ox轴夹角,rad。令sθi=sinθi,cθi=cosθi,θ可用式(6)计算:

(6)

从动臂的质心的位置分别为

(7)

动平台的质心为

P5=(P5x,P5y,P5z)。

(8)

式(8)中,P5x、P5y、P5z分别为

(9)

对式(1)求导,可以求得电机M1、M2、M3、M4的质心的速度为

(10)

对式(3)求导,主动臂的质心平动速度分别为

(11)

对式(4)求导,主从动臂间连接件的质心速度分别为

(12)

对式(7)求导,从动臂的质心的速度分别为

(13)

对式(9)求导,动平台的质心在三个方向上的速度分别为

(14)

动平台质心的速度即为

v5=(v5x,v5y,v5z)。

(15)

2.3 动能与势能

在连杆-质点等效模型中,部件1、3被视作质点,仅有平动动能,而部件2、4、5被视作连杆,动能为平动和转动两部分动能之和。五种部件的动能表示如下:

(16)

式(16)中:mi为各个类型单个部件的质量,其中i∈{1,2,3,4,5},kg;J2x、J2y、J5z分别为部件2、4、5经过各自质心在相应方向上的转动惯量,kg·m2。

则此模型的总动能为

(17)

以xOy平面为零势能面,5种部件的势能表示如下:

(18)

则此模型的总势能为

(19)

2.4 拉格朗日动力学方程

(20)

那么本系统中的电机在控制在y轴上的移动变量时,需要的施加在运动方向y上的合力应分别为

(21)

3 动力学近似建模方法

本文的实验条件如下:使用的MATLAB版本为R2020b,设备品牌型号为Lenovo Xiaoxin 510S-141KB,中央处理器的型号为Intel(R) Core(TM) i7-7500U CPU @ 2.70 GHz 2.90 GHz,操作系统的类型为64位操作系统,基于x64的处理器。

使用MATLAB对以上模型动力学方程进行计算,单个电机推力方程的推演时间大于5 s,包括加减乘除乘方在内的计算次数大于23 000次。将电机的位置动态轨迹[13]设为

(22)

将式(22)所示的动态轨迹代入到用拉格朗日函数方法求得的动力学模型中计算,单次单个电机的计算时间大于16 s,计算量大,计算时间长,故无法满足实际运用时实时解算的要求。本文采用的近似方法均为在前一步骤的基础上进行下一步近似,以期获得在不同精度和实时性要求下可以采用的简化模型。

3.1 基于小角度几何近似的模型简化

被动角的精确计算涉及多个参数和变量,计算复杂,但其量值在后续模型计算中涉及颇多。根据在实际系统中动平台长度较小的特点,本文在此提出一种基于小角度几何近似的简化方法,以减少模型计算量。

图3 小角度几何近似示意图Figure 3 Schematic diagram of small angle geometric approximation

(23)

(24)

式(25)中,Δz为两侧部件3质心之间的高度差,即

Δz=l2(sinα1-sinα2)。

(25)

那么近似的被动角可以表示为式(26):

(26)

对被动角度进行近似后,用MATLAB对动力学方程进行计算,单个电机推力方程的推演时间约为4.171 s左右,计算次数为13 867次,对同一动态轨迹的计算时间约为12.657 s。

3.2 基于等效均质杆的模型简化

以上连杆-质点等效模型在运动学分析时忽略了小偏置,为后续动力学建模计算提供了便捷,为更进一步减少参数,现将其中全部连杆视为均质杆,部件的质点位于其几何中心处。

那么主动臂相对于质心的转动惯量为

(27)

式(27)中,ρ为杆件密度,ρ=m2/l2,kg/m。同理可得

对于模型的实际应用而言,代换后减少了待辨识的动力学参数[14],并将动力学方程中的同类项进行合并,用MATLAB对动力学方程进行计算,单个电机推力方程的推演时间约为2.051 s,计算次数为6 259次,对同一动态轨迹的计算时间约为4.279 s,进一步简化了模型,减少了计算量。

3.3 基于等效集中质量的模型简化

图4 等效集中质量分布图Figure 4 Equivalent concentrate mass distribution diagram

用MATLAB对动力学方程进行计算,单个电机推力方程的推演时间约为1.788 s左右,计算次数为6 215次,对同一动态轨迹的计算时间约为3.690 s。

4 动力学仿真分析

为了验证以上动力学简化模型的可行性和精确度,在ADAMS中导入已有的相同构型的虚拟样机,进行仿真实验以对以上简化模型进行验证,验证策略[17]如图5。

图5 验证策略流程图Figure 5 Flow chart of verification strategy

在ADAMS中读取虚拟样机的动力学参数取值如表1。

4.1 几何参数反向标定

使电机的质心的位置分别为

(28)

在ADAMS中读取虚拟样机的几何参数取值如表2。

表2 四自由度3T1R并联机器人的几何参数取值(反向标定前)

计算得到电机M1上的力约为18.986 3 N,ADAMS中仿真结果为23.864 4 N,两者相差20.440 9%。要让数学模型计算达到较高的绝对精度,获得合适的运动学参数是十分必要的[18]。据以上数据对数学模型中的几何参数进行反向标定,反向标定后结果见表3。

表3 四自由度3T1R并联机器人的几何参数取值(反向标定后)

对比表2和表3,可见反向标定后有些参数偏差较大,如l4、L,其他参数也有不同程度的偏差。导致反向标定前后的偏差原因有很多,如在动力学建模过程中对多种要素的理想化、近似建模及人工测距等。也正是由于几何参数名义值代入模型进行解算的结果不准确,所以需要对数学模型中的几何参数进行反向标定。

4.2 结果对比与分析

4.2.1 轨迹选择

基于机器人的分拣功能,将电机在y轴上的位置动态轨迹设为多段三次多项式,相关多项式的系数矩阵如表4。

表4 电机动态轨迹系数表

各个电机在y轴上的运动轨迹如图6。将该轨迹输入ADAMS进行仿真实验,仿真时间设为1 s,步数为100步。

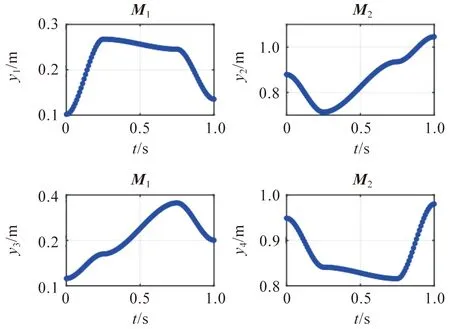
图6 电机运动轨迹Figure 6 Figure of track of motor motion

4.2.2 结果对比

将ADAMS中的推力仿真结果导出到MATLAB中,与未简化的等效模型的计算结果进行对比,结果如图7。

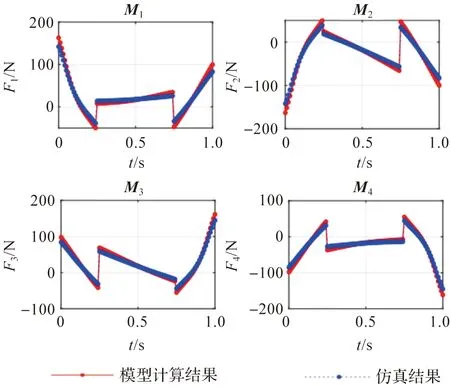
图7 动力学模型与仿真力曲线对比图Figure 7 Comparison diagram between dynamic model and simulation force curve

未简化模型的计算结果与ADAMS中仿真结果间的相关系数均在0.99以上,总体吻合程度良好,验证了动力学模型的准确性。在同一轨迹下,用MATLAB对不同程度简化后的数学模型进行解算,并与仿真结果进行比较,结果如图8～10。简化后模型的计算结果与ADAMS中仿真结果间的相关系数均在0.98以上,为强线性相关程度,曲线吻合程度高[19]。

图8 小角度几何近似模型力曲线对比图Figure 8 Comparison diagram of force curve of small angle geometric approximate model

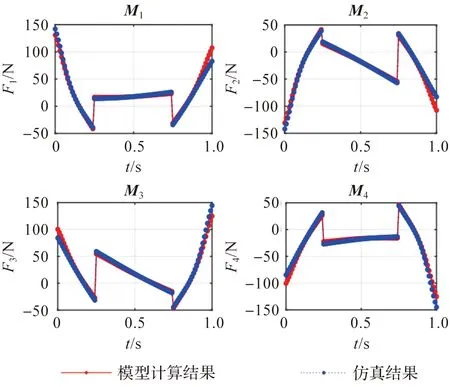
图9 基于等效均质杆模型力曲线对比图Figure 9 Comparison diagram of force curve based on equivalent homogeneous bar model

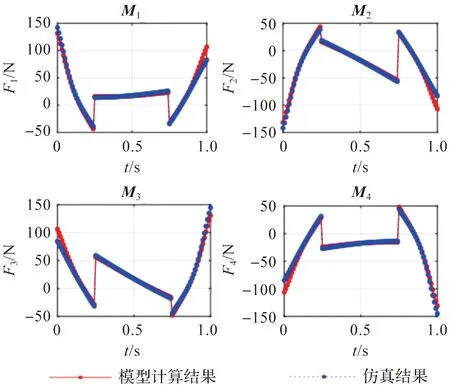
图10 基于等效集中质量简化模型力曲线对比图Figure 10 Comparison diagram of force curve based on equivalent concentrate mass simplified model

4.2.3 结果分析

分析各个模型解算结果与ADAMS中仿真结果间的均方误差,如图11。

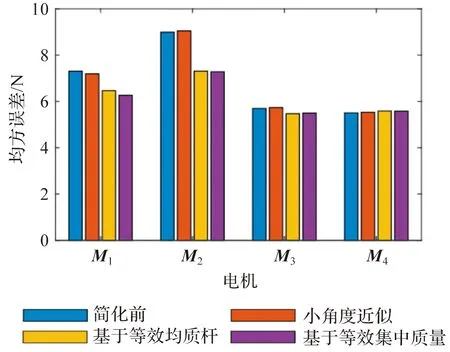
图11 各个模型的均方误差Figure 11 Mean square error of each model

分析机器人运动过程中,各个模型解算结果与ADAMS中仿真结果间的实时绝对误差,如图12。

图12 各个模型的绝对误差Figure 12 Relative error of starting time of each model

由以上误差分析可知,在该轨迹下,误差并没有在简化并联机器人动力学模型的过程中持续扩大,小角度几何近似模型误差带的偏移量较大,随着模型进一步简化,基于等效均质杆模型和等效集中质量简化模型计算效果较优。

采用被动关节角小角度近似-等效均质杆-等效集中质量模型顺次近似后,计算步骤和时间的减少幅度如表5,在保证精确度的同时,大幅减少了所需的计算时间和计算量。

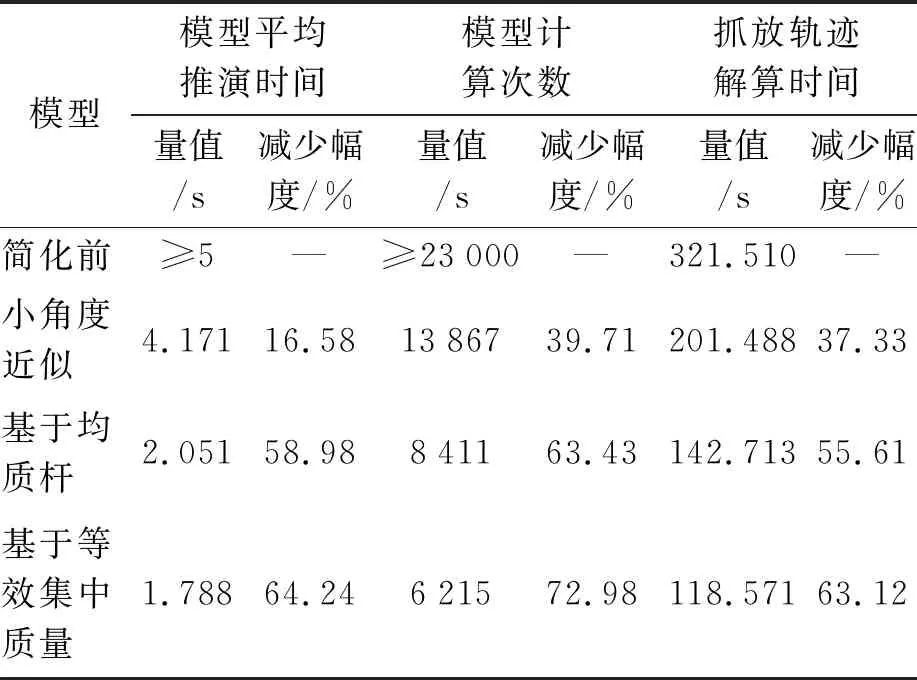
表5 动力学顺次近似模型简化程度

5 结 语

本文针对应用于分拣的四自由度3T1R并联机器人的动力学分析和近似建模问题,利用并联机器人的几何对称性质,在被动关节角的计算上进行了近似,并在此基础上对该机器人的杆件和质量分布进行了进一步的近似。

对于给定的分拣轨迹,利用ADAMS和MATLAB对机器人进行动力学仿真和分析,证明在该轨迹下,简化后动力学模型能够在保证精确度的同时,减少计算步骤和时间。