建筑业上市公司财务风险度量研究——基于GARCH-MIDAS-VaR模型

王文胜,包智瑜

(杭州电子科技大学 经济学院,浙江 杭州 310018)

2021年新冠疫情的爆发,使得全球经济遭受严重打击,各国面临经济下行所带来的压力。从宏观角度来看,经济泡沫,熔断效应,进出口受阻,对各国经济发展造成严重损害;从微观角度而言,实体经济遭受重创,小微企业融资难,居民消费放缓,拖欠贷款,各种经济问题接踵而至。因此,无论从宏观审慎还是微观审慎角度,实现对金融风险的测度是关键之处。其中,财务风险的度量对反映企业的风险管理水平至关重要,在此种百年未有之大变局下,对投资者的利益也具有深刻的意义。

一、文献回顾与研究动机

在研究金融时间序列波动率时,传统的计量经济学模型,均假设扰动项方差为常数,无法准确刻画金融时间序列所具有的异方差性,Engle(1982)[1]首次提出自回归条件异方差模型(ARCH模型),根据历史信息来预测未来波动率,但该模型在用于精确刻画金融数据的波动聚集特征时,要求较大滞后阶数,极大增加了估计量。因此,Bollerslev(1986)[2]提出广义自回归条件异方差模型(GARCH模型),解决了ARCH模型的高阶滞后问题,实证表明该模型能更有助于度量数据波动的聚集性和长记忆性。但以往的研究都未考虑到金融数据的混频特征,Ghysels等(2006)[3]针对该问题提出了混频数据抽样模型(Mixed Data Sampling,MIDAS),无须对数据进行降频升频处理,可直接利用高频经济数据对宏观经济总量等低频信息进行预测,保留了所有原始信息,避免了处理同频数据时所引起的信息虚增,提高了预测精度,有效解决了模型预设问题。刘汉和刘金全(2011)[4]利用MIDAS模型对我国GDP增长率进行了实时预测,结果显示:相比于同频数据的直接预测,该模型更具有比较优势。根据GARCH模型在度量数据波动的聚集性上的优势,Engle和Ghysels(2013)[5]开始将混频模型与该模型结合,首先提出了单因子混频GARCH模型(GARCH-MIDAS模型),即将股市波动分解为长期和短期波动,短期波动由历史波动信息来决定,即GARCH模型,而长期波动部分则通过低频宏观经济变量来刻画,即MIDAS模型。Christian和Karin(2015)[6]利用混频GARCH-MIDAS模型深入研究了工业增加值、失业率等多种宏观因素对美国标普500指数长期波动的影响。夏婷和闻岳春(2018)[7]和王新宇等(2018)[8]都将该模型用于对债券收益波动率的研究,前者在Engle和Ghysels(2013)[5]原有的研究变量中,引入经济不确定性指标,从宏观经济不确定性以及经济政策不确定性两个方面进行研究。后者则分别建立低频宏观经济变量和高频宏观经济变量GARCH-MIDAS模型,对债券市场进行风险测量。

对于度量财务风险而言,国外最早出现的是统计学单分类方法,Edward(1968)[9]通过多元判别分析(MDA)得到企业综合风险值Z值,将其与临界值对比,从而得出企业的风险严重程度。利用22个财务比率作为解释变量,得到Z计分模型(Z-score)。徐凯等(2014)[10]利用Z-Score模型对医药公司进行实证研究,研究显示Z值越大企业财务状况越好,反之越差。除了使用上述财务指标,VaR(在险价值)作为度量风险的方法,也被广泛应用于反映企业的财务状况,VaR的计算方法主要有参数法、蒙特卡罗模拟法、历史模拟法等。其中,运用最多的是参数法,众多学者将其结合金融时间序列模型,进行企业财务风险的度量与预测。例如,曹兴和胡高(2009)[11]使用逻辑回归模型预测财务风险时,概括了一系列财务指标后,又引入VaR指标共同构成度量指标体系,探讨VaR参量对识别企业财务风险的统计影响程度。杨国臣和黄翔(2013)[12]用GARCH模型计算VaR指标,较好地描述了股指序列的波动,克服了传统的静态VaR计算方法不能很好刻画时间序列数据波动聚集性特征的问题。许院院和刁节文(2015)[13]通过三种不同分布的GARCH族模型计算银行间同业拆借头寸的VaR值,并使用模型分析各银行利率及风险状况差异。邓亚昊(2013)[14]将GARCH模型用于房地产上市公司的财务风险的预测中,通过将GARCH模型所计算出的VaR建立VaR自回归模型,从而实现对企业VaR的预测,以此度量企业财务风险状况。郑平(2014)[15]利用GARCH模型族分别对沪深300指数VaR进行度量,用Eviews绘制出实际损益率,与VaR作对比,检验不同模型的失败率,结果表明GARCH、TGARCH、EGARCH模型其失败次数均能落在95%水平上。申利(2018)[16]在分析比较经典的方差-协方差法、历史模拟法和蒙特卡罗法计算VaR的基础上,构建GARCH-VaR模型,测度人民币/美元的外汇风险,结果表明VaR方法是一种有效的外汇风险度量方法。林文豪等(2019)[17]利用DQ检验等统计量来比较历史模拟法、RiskMetrics以及GARCH(1,1)模型族共15种模型对VaR模型的预测效果,通过各项检验找寻出拟合度更高的风险管理组合。王颖(2020)[18]在使用财务指标与VaR构建logistic模型对企业财务风险进行预警时,融入了行业集中度指标,实证表明该模型的预测准确性更高。

陈璐(2021)[19]使用混频数据分析方法测度了金融风险,但并未涉及对上市公司财务风险预测。李存(2021)[20]将混频抽样模型与逻辑回归模型相结合,引入了混频的财务指标与宏观经济指标,建立了上市公司财务风险预警模型。常佳宁(2022)[21]将GARCH-MIDAS模型与极值理论结合,用于预测原油市场VaR值。然而,尚未有研究将混频GARCH模型应用于对财务风险度量当中。相比以往研究,本文的改进之处在于:使用GARCH-MIDAS模型进行VaR度量,以此反映企业财务风险状况。与传统的选取已实现波动率或一些宏观经济变量作为模型中低频变量的思路不同,本文参考邓亚昊(2013)[14]度量财务风险的方法,选取22个上市公司季度频率财务指标数据,并通过熵权法计算这些财务指标的一个综合值,将该综合值作为低频变量,上市公司的股票日度收益率作为高频变量,引入GARCH-MIDAS模型,利用该模型估计出条件波动率,最后通过参数法计算出VaR,与股票实际的收益率作对比。在多头头寸(岳婷婷,2019)[22]下,比较GARCH模型和GARCH-MIDAS模型对于VaR的度量效果。

二、模型简述及度量方法

(一)模型构建

1.GARCH模型

在对于波动率的预测当中,由于ARCH模型存在高阶误差问题,对参数要求过大。GARCH模型的出现,很好地解决了此问题。其表达式如下:

(1)

(2)

(3)

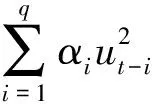
在传统的GARCH模型中,GARCH(1,1)模型对于金融时间序列数据的拟合具有很好的效果,因此,本文考虑使用GARCH(1,1)模型进行研究,即上式的p与q都取1。

2.GARCH-MIDAS模型

为了纳入不同频率数据,实现用高频数据预测低频波动率,并同时考虑到时间序列数据的波动聚集效应,Engle和Ghysels(2013)[5]将GARCH模型与MIDAS模型相结合,提出GARCH-MIDAS模型。将股票价格波动(条件方差)分解为短期(高频)成分与长期(低频)成分。长期成分通常通过类似于已实现波动率等低频变量进行刻画,短期成分一般由股票市场日内交易信息等流动性影响因子反映,服从GARCH模型。实际当中选择较低阶数往往使得结果表现更好,一般认为日度波动率动态成分服从一般的GARCH(1,1)过程。

GARCH-MIDAS模型如下:

(4)

式(4)为均值方程,其中,ri,t代表股票日内交易信息,表示第t个月第i天的收益率情况,通常取日度收益率的对数差分εi,t为随机扰动项,服从条件标准正态分布,即,εi,t|Φi-1,t～N(0,1),Φi-1,t表示t月第i-1天可获取的信息集。u代表收益率条件期望。短期高频波动率服从GARCH(1,1)过程:

(5)

式(4)和(5)中,τt为基于MIDAS回归方程的平滑实现波动率,代表长期低频成分,由某些低频变量进行刻画,α与β为参数,α>0,β>0,且α+β<1。MIDAS模型计算τt公式如下:

(6)

(7)

τtgi,t共同构成了对数收益率的条件方差σt,代表滞后k期的低频变量,通常选择已实现波动率或宏观低频数据进行刻画,K为最大滞后阶数,一般通过AIC或BIC准则进行确定。θ体现低频变量对长期波动成分的影响程度。φk(ω1,ω2)表示权重函数,根据苏治等(2018)[23]关于混频GARCH模型不同权重函数的叙述,本文考虑Beta非限制性权重函数进行研究。即如式(7)所示,此时的权重具有时变衰减性。ω1,ω2为待估参数,有ω1>0,ω2≥1,并为进一步简化模型,参照Wang等(2020)[24],令ω1为1,此时,φk(1,ω2)是关于ω2的单调函数。由此,式(4)、(5)、(6)、(7)共同构成GARCH-MIDAS模型。

3.GJR-GARCH-MIDAS模型

由于不同的市场信息对股票价格的冲击所造成的影响是不对称的,人们往往对价格下跌的反应比价格上涨更激烈,即利空消息对价格变化的影响大于利好消息,存在由负性冲击所产生的杠杆效应。因此,Christian与Karin(2015)[6]在以上模型的基础上使用了GJR-GARCH-MIDAS模型,用于衡量市场信息的非对称效应。韩娅玲(2021)[25]运用扩展的GARCH-MIDAS(GARCH-MIDAS-A)模型,在长期和短期波动中都引入了不对称效应,对上证指数波动性进行分析。本文为了简化模型,参照Christian与Karin(2015)[6],只考虑短期的GARCH(1,1)模型部分的非对称性,长期不考虑。GJR(1,1)模型短期波动过程建模如下:

(8)

此时对应约束条件变为:α+β+0.5γ<1其中,I{·}为示性函数,即满足条件时取1,反之取0,体现了市场消息对股票价格冲击影响的不对称性。当市场存在利空消息时,即消息对股价造成了负面影响,对应ri-1,t<0,I{·}取0;反之,当市场不存在利空消息时,对应ri-1,t≥0,I{·}取1。此时,公式(4)、(6)、(7)、(8)共同构成GJR-GARCH-MIDAS模型。

(二)度量方法

VaR即在险价值,指金融资产或其组合的市场价格,在一定持有期内和一定置信水平下所可能遭受的最大损失,即损失分布的第(1-α)分位数,能够较准确地度量市场风险,适应金融市场发展的动态性。对VaR的计算方法主要有历史模拟法、蒙特卡罗模拟法、参数法。其中应用最广泛的是参数法,具体原理如下:

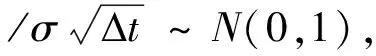
通过参数法计算的VaR,相较于前两种方法,拟合效果更高,计算更简单,基于此,本文选择参数法对金融时间序列进行VaR的度量,以此反映企业风险状况,同时考虑到金融数据具有的混频性质,本文采用上文提到的混频模型度量VaR。

三、上市企业财务风险度量的实证分析

为了说明考虑了数据混频特征的模型相较于标准的GARCH模型在度量VaR上有更好的效果,本文将标准GARCH模型、GARCH-MIDAS模型、GJR-GARCH-MIDAS模型分别用于上市企业的实际交易数据,对比分析各个模型的度量结果。

(一)数据来源

近年来我国经济面临下行压力,实体经济发展不容乐观,建筑业作为实体经济的组成部分,是我国三大支柱产业之一,于国民经济有着举足轻重的地位。因此,本文选取我国建筑业上市公司2016—2020年股票日收盘价与季度财务指标作为样本数据进行研究。获得样本后,需进行数据预处理,首先除去数据缺失较多的部分公司,数据缺失较少的公司再使用其对应指标的均值进行填补,最终经过处理后选取了20家建筑业上市公司的相应数据,进一步进行VaR的计算。

公司名称及所对应的证券代码如下表1所示:

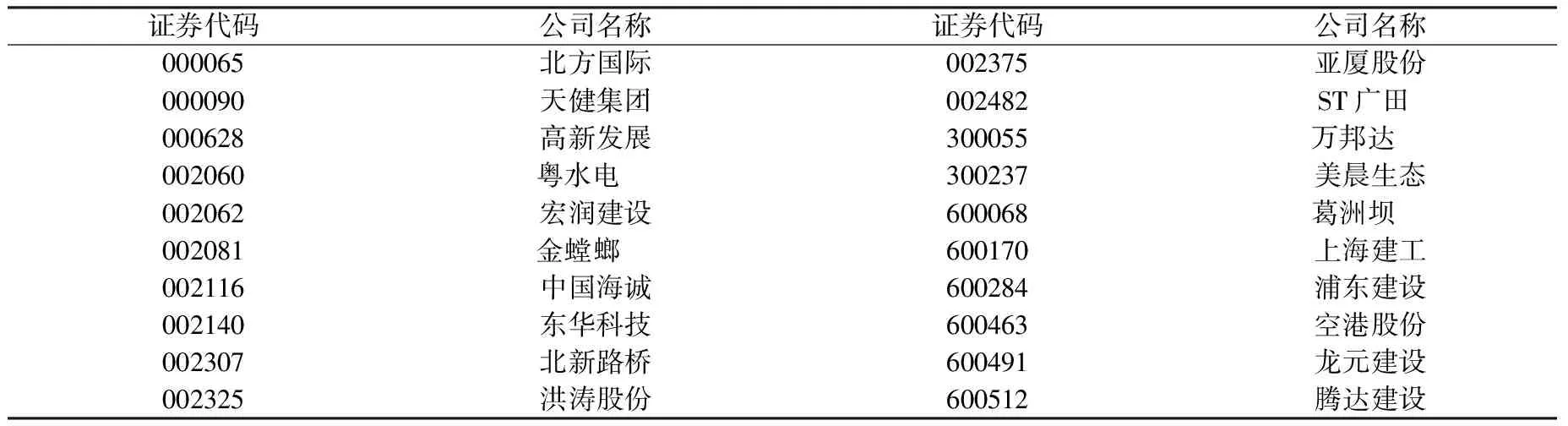
表1 样本上市公司证券代码及企业名称

以上数据来源于国泰安数据库,大智慧股票分析软件。

对于收益率的计算本文采用几何(对数)收益率,具体公式如下:

ri,t=ln(Pi/Pi-1)

(9)

其中,Pi为样本公司第i日收盘价,Pi-1为第i-1日收盘价,ri,t为经过处理后的第t个月第i天的对数收益率。

(二)指标选取与处理

本文参照以往文献,根据全面性、参照性及作用性原则,分别从盈利能力、经营能力、成长能力、发展能力四个方面,共选取22个季度财务指标进行研究,具体指标如下表2所示:

表2 财务指标变量

由于各个财务指标之间量纲不同,需要先对数据进行标准化处理。处理方法如下:

(10)

其中,xij为第i季度第j个财务指标值,i=1,2…20,j=1,2,3…22。

与以往文献建立财务指标体系并进行主成分分析提取关键因子不同,本文旨在利用财务指标数据作为一部分解释变量融入混频模型进行VaR的度量,从而体现模型对企业财务风险的反映状况。

因此,对于GARCH-MIDAS模型,GJR-GARCH-MIDAS模型中的低频变量的选择,本文并未参照以往文献使用已实现波动率或宏观经济变量,为了体现VaR指标对于财务风险的反映,本文使用邓亚昊(2013)[14]的处理方法,根据熵权法计算出一个可以综合评价22个财务指标的值,将该值作为低频变量引入混频模型中计算VaR。计算公式如下:

(11)

其中,aj为第j个财务指标的熵值,t为每项财务指标值的数量,样本区间为2016—2020年,此时t=20,pij为每个财务指标取不同值的概率,计算过程为:

(12)

由此求出每个财务指标值所对应的权重:

(13)

其中,m为财务指标的个数,即m=22,最后计算出财务指标综合值wj

(14)

将wj作为低频变量,代入GARCH-MIDAS与GJR-GARCH-MIDAS模型中,由于GARCH模型没有考虑混频数据,只是作为对照,因此wj无须代入该模型。

(三)VaR度量

传统的测度金融市场风险的方法单一,对于复杂的资产组合不能进行有效的风险测量,VaR(在险价值)的概念提出解决了这一问题,目前,在计算VaR的方法中,方差-协方差法应用较为普遍,因此,本文采取方差-协方差法度量VaR,参照岳婷婷(2019)[22]采用多头VaR的计算公式,具体表达式如下:

(15)

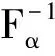
上一节已指出GARCH、GARCH-MIDAS、GJR-GARCH-MIDAS模型的表达式,因此,本文分别将样本公司的数据拟合三个模型,GARCH-MIDAS与GJR-GARCH-MIDAS模型还需要加入上文计算出的财务指标综合值wj作为低频变量,计算出三个模型的条件方差σt即公式(15)中ht,再利用该公式计算样本公司VaR值。

(四)返回测试

通过上述方程实现了三个模型对VaR的度量,但VaR作为一个估计值,其有效性还要进行检验,以此比较不同模型对财务风险的度量效果。因此,本文采用返回测试技术进行验证。

Kupiec的似然比检验是通过计算失败率与设定值P0是否相等来比较模型的预测准确度。记金融数据某一时点的实际损失大于VaR值为一次预测失败,则失败率可定义为:P=N/T,

其中,T为所考察样本区间的总天数,N为失败的天数,即实际损失大于VaR的天数。原假设为P=P0,即失败率与设定值P0值相等。再分别对GARCH、GARCH-MIDAS、GJR-GARCH-MIDAS三个模型在95%显著水平下进行似然比检验,检验统计量为:

(16)

考虑到20个样本公司2016—2020年的日度收益率的总天数都不相同,因此,统一选取每个公司样本区间的最后1 000天日度收益率数据进行Kupiec检验,统计检验区间内每个公司实际损失大于VaR的天数。结果如下表3所示:

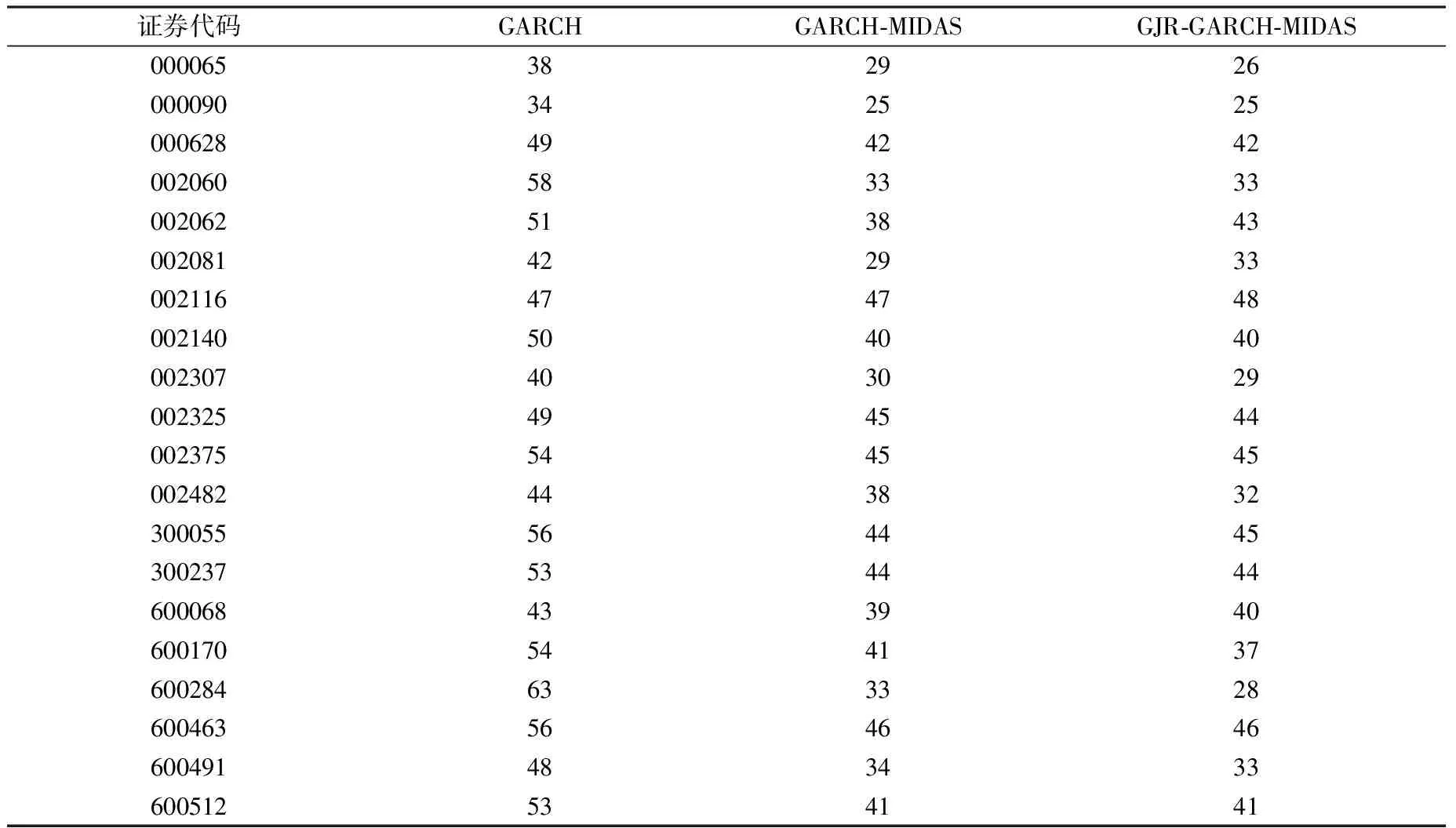
表3 样本公司实际损失大于VaR天数统计表

根据表中结果可知:

在95%显著水平下,GARCH模型拒绝了原假设,即存在一些样本公司数据使得实际失败天数大于理论失败天数。GARCH-MIDAS模型与GJR-GARCH-MIDAS模型均不拒绝原假设,实际失败天数都小于理论失败天数,且每个样本数据对应的预测失败天数都比GARCH模型小,预测精度更高。两个模型的失败天数接近,预测效果差异不大。

三个模型分别对各个企业的预测失败天数的纵向比较而言,失败天数越多的企业,说明股票实际收益率波动更剧烈,VaR指标不能更准确刻画损益率的变化情况,该公司相对其他公司而言,面临更大的财务风险。

为了更充分直观说明三个模型的度量状况,本文画出样本公司对应的实际损益率与VaR效果图,但由于文章篇幅有限,在20个样本公司中,选取了四家公司画图进行分析,如图1所示。

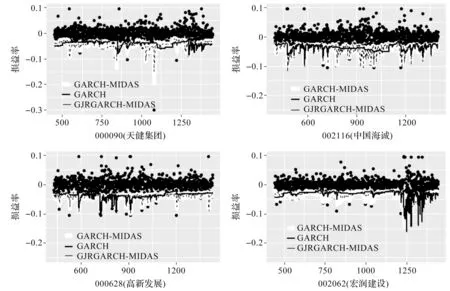
图1 三种模型估计的样本公司VaR

图1中,混频模型的VaR相比于传统GARCH模型起伏更大,而GARCH模型较为平稳,不能很好预测出收益率的波动情况,混频模型对上市公司股票日度收益率的最大损失预测更为准确,更能及时捕捉到企业财务风险状况;此外,GARCH-MIDAS模型与GJR-GARCH-MIDAS模型的高低起伏基本吻合,表明二者在度量VaR上效果差异不大。

四、结论与建议

本文通过对20家建筑业上市公司2016—2020年股票日度收益率数据及财务指标进行VaR计算,得到如下结论:与以往文献将诸如已实现波动率等指标作为模型中低频变量来研究金融数据波动率不同,本文将一系列财务指标通过熵权法计算出综合值作为新的低频变量,引入GARCH-MIDAS模型并使用参数法计算VaR,以此反映企业财务风险状况是可行的,说明此种处理方法具有一定的实际意义。GARCH、GARCH-MIDAS及GJR-GARCH-MIDAS三个模型所计算出的VaR在与收益率的比较当中,GARCH模型失败次数不能全落在95%水平上,而考虑了混频因素的GARCH-MIDAS模型与GJR-GARCH-MIDAS模型均能落在95%水平上,且预测失败率都小于GARCH模型,说明将财务指标引入混频模型从而度量财务风险的准确性更高。最后,考虑了市场信息非对称性的GJR-GARCH-MIDAS模型的检验结果,与未考虑市场信息非对称性的GARCH-MIDAS模型的结果非常相近,说明市场信息不对称性因素对于建筑业公司财务风险状况的影响并不大。基于以上结论,本文提出如下建议:

(一)混频数据模型可以应用于公司财务风险度量中

混频数据模型考虑了财务指标的频率不一致问题,可同时保留高频数据与低频数据,进行财务风险的度量,相比于以往单纯建立财务指标体系刻画风险,具有更高的预测精度。在今后对财务风险的研究中,可充分利用混频模型进行分析。

(二)研究变量可进一步扩大,提高风险预测精度

本文只是将财务指标作为低频变量引入模型,但影响财务风险的类似宏观经济变量等非财务因素并未纳入模型,因此,后续可以在模型中进一步扩大研究变量的范围,使得财务风险的评价体系更完整。