铀酰叠氮离子化合物的质谱分析与理论计算

洪 静,韩昌财,费泽杰,唐圆圆,刘艳成,周露露,刘洪涛,熊孝根,董常武,*

1.中国科学院 上海应用物理研究所,上海 201800;2.中国科学院大学,北京 100049;3.同济大学 化学科学与工程学院,上海 200092;4.山东能源集团有限公司,山东 济南 250101;5.中山大学 中法核工程与技术学院,广东 珠海 519082

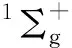
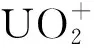
The exploration of equatorial coordination number CNeqis also one of the points of interest. Meanwhile, the rise of uranium nitride as a new type of nuclear fuel has attracted a lot of attention, U-N bonding interactions have also aroused extensive exploration. In the study on [NUⅥO]+by Zhao et al.[21], a series of complexes with [NUⅥO]+cations as the core and N2as the equatorial ligand were synthesized in the gas phase. The complete spatial saturation of the linear [NUⅥO]+at an equatorial coordination number of 5, that is [NUO(N2)5]+, was confirmed by mass spectrometry-selected infrared photodissociation spectroscopy and quantum chemical calculations. Nevertheless, in Marks’ photodissociation and infrared spectroscopy investigation of U+(N2)ncomplexes, the saturated coordination complex was predicted to be U+(N2)8with a cubic structure[22].

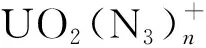
1 Experimental

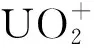
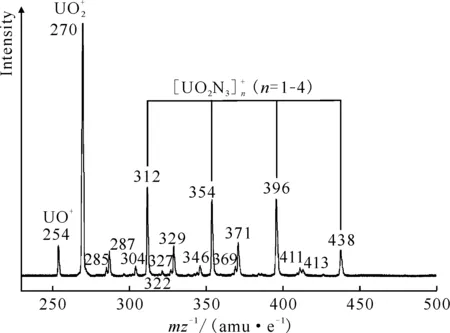
m/z range: 200-500 amu/eFig.1 Mass spectrum of the cluster cations formed by pulsed-laser vaporization of a uranium target in an expansion of nitrous oxide gas

2 Calculational

DFT calculations using the Gaussian 09 software packages[25]were carried out on the geometries, vibrational frequencies, and electronic structures of the title complexes by the hybrid density functional B3LYP(Becke three-parameter hybrid functional combined with Lee-Yang-Parr correlation functional)[26]. The vibrational frequency analysis calculations was also performed at the same level of theory to confirm the obtained structures to be true minima. The correlation-consistent triple-ξ(cc-pVTZ) basis sets were employed for N and O atoms[27], and the scalar-relativistic(SR) effective small-core potential ECP60MDF and the corresponding correlation-consistent polarized triple-ξ basis sets(cc-pVTZ-PP)[28-29]were used for U atom. For convenience, we will call the basis sets used in this study as VTZ-PP hereafter. The ligand bonding energies were carried out for the formation of the reactions [UO2]++nN3→[UO2(N3)n]+(n=1-4).

The bond order analyses, including Mayer, Wiberg and Fuzzy methods were performed using the Multiwfn software package[30]. We also used the NBO 7.0 program[31]to carry out the natural population analysis(NPA), NBO spin analysis and natural localized valence MO(NLMO) analyses to illustrate the bonding properties between the uranyl unit and the ligands.

3 Results and discussion

3.1 Geometric structure of and [UO2(N3)n]+(n=1-4)

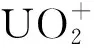
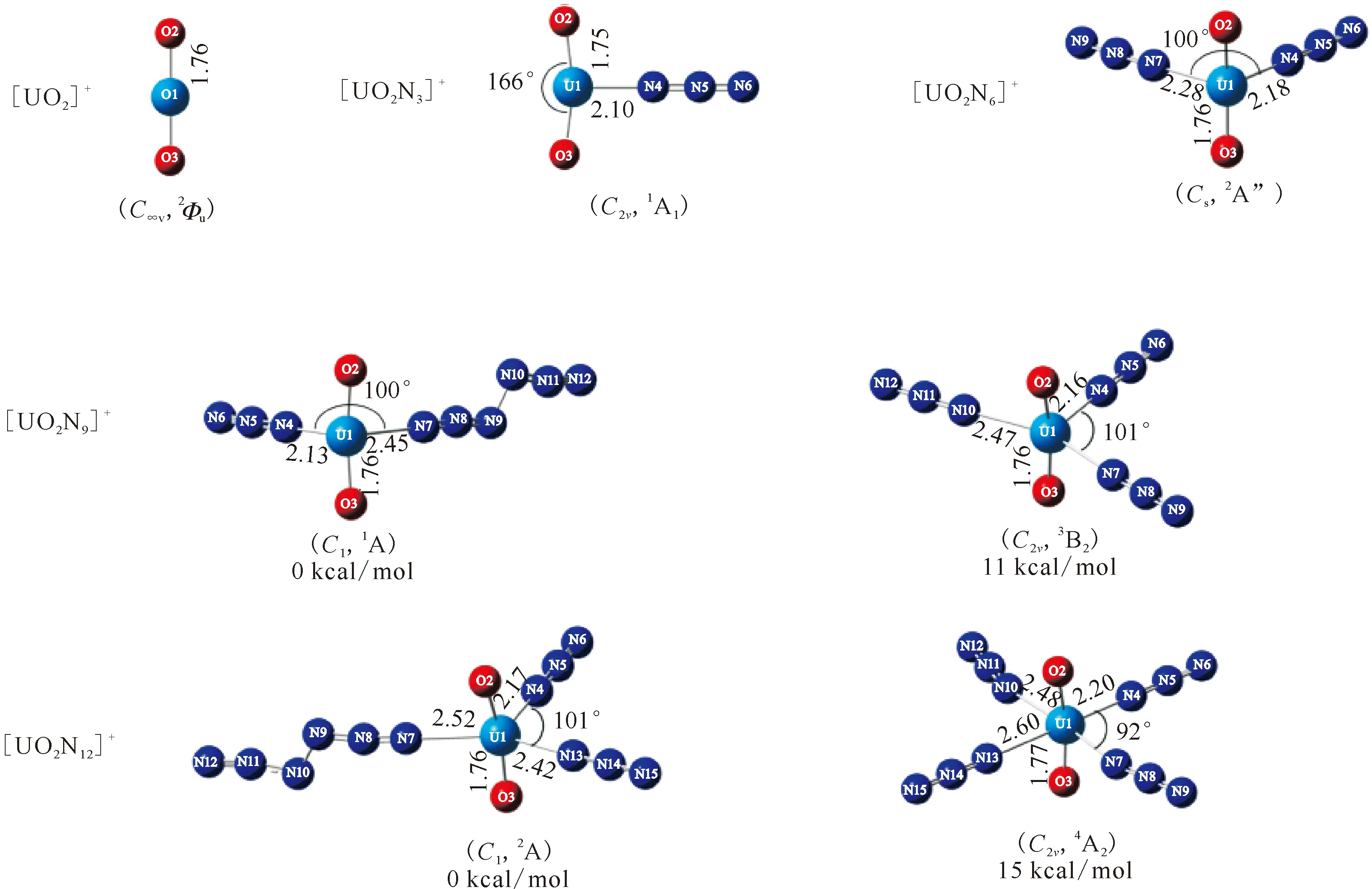
1 cal=4.187 JThe relative energies(kcal/mol), bond length(Å) and bond angle(°) are also givenFig.2 Optimized geometries, symmetries and electronic configurations for the ground state and [UO2(N3)n]+(n=1-4) calculated at the SR-B3LYP/VTZ-PP level

The [UO2N6]+is calculated as the second N3ligand(L2) continues to be coordinated to U on the equatorial plane. The most stable structure is obtained showing the2A″ ground state withCssymmetry. The U-L2(U1-N7) bond length is calculated to be 2.28 Å, which is also shorter than the sum of single-bond covalent radii for the U and N elements. Meanwhile, as the L2 coordinated to U, the U-O and U-L1 bond length are all slightly weakened and elongated by 0.01 Å and 0.08 Å, respectively.

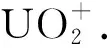
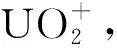
3.2 Equatorial coordination

Throughout the previous studies, the equatorial coordination numbers of ions with uranium atoms as central atoms span a wide range. The series represented by halogenated uranyl complexes[7, 34-35]have the same coordination number CNeq=4 as in the present work; the ligands of the CNeq=5 complexes include CO, H2O and some rare gas atoms[20, 36-40]. Some of the smaller rare gas atoms(Ne, He)[38]can reach larger coordination numbers such as CNeq=6; further up there are complexes with pure naked uranium atoms U+as the central ion, where there is an octa-coordination of CNeq=8 in the case of CO and N2ligands[22, 37].This can be explained by the parameterQ, defined as the ratio of the “ligand van der Waals diameter” to the “bond length of center to ligand”[21], which symbolizes the limitation of the coordination number by the size of the ligand space. The dependence betweenQand CNeqcan be expressed asQ≤1 for CNeq=6;Q∈(1.1, 1.2) for CNeq=5;Q≥1.2 for CNeq=4. In this paper, the N3radical van der Waals diameter is determined to be about 3.5 Å and the distance between N3radical and U atom is taken as the average of the U-N bond length, which is 2.438 Å, so that the value ofQis 3.5/2.438=1.44, which is greater than 1.2, providing an explanation for the CNeq=4 of [UO2(N3)4]+with N3radical as the ligand. Interestingly, in the structure optimization, cluster with N6ligand is also obtained and the energy is slightly lower than that with pure N3ligands. According to the judgement about parameterQ, the van der Waals diameter of N6should be much larger than 3.5 Å, thus theQshould be even larger than 1.44. That means the mass signals ofn>4 for [UO2(N3)n]+clusters should be observed in the experiment. However, the mass spectra shows that no complex ions withn>4 are produced, so it is reasonable to assume that saturation coordination has been reached at [UO2(N3)4]+with N3radical as the ligand. And the discussion below will only consider the equatorial coordination model with N3as the ligand rather than N6.

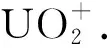
(a): Total ligand-bonding energy (b): Differential bonding energy of the last additional N3 ligand(δEb= E([UO2(N3)n]+)-E([UO2(N3)n-1]+)-E(N3) (n=1-4))Fig.3 The coordination energies of [UO2(N3)n]+vs. equatorial coordination number n=0 or 1 to 4

The δEbof L1 is much larger than others since it forms the U-L1 chemical bond.

3.3 Bond distances of U-O and U-N bonds

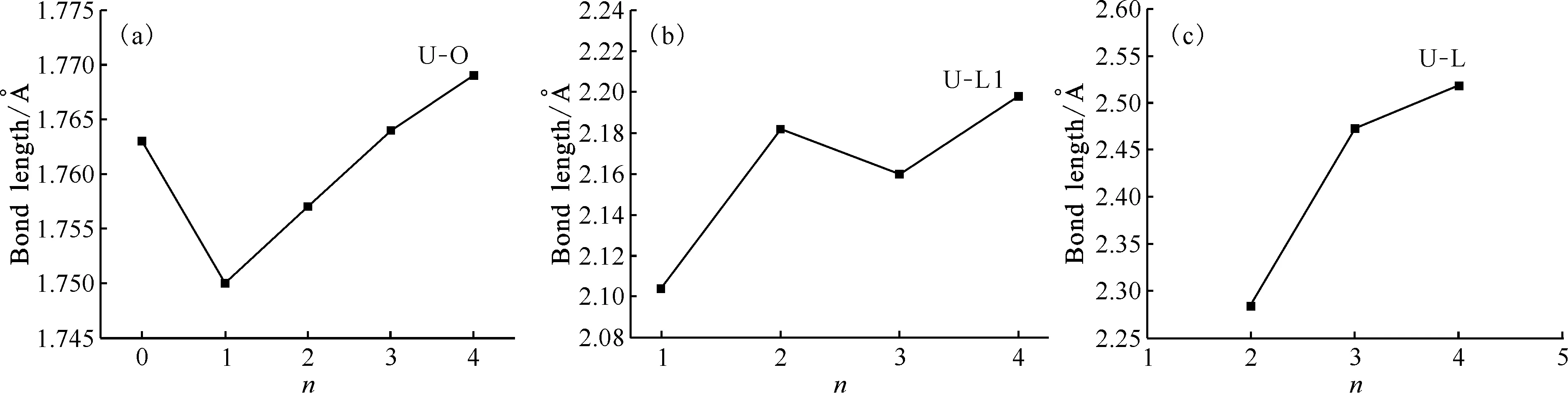
Fig.4 The bond lengths of U-O(a), U-L1(b) and average bond lengths of U-L(c) vs coordination number n

The situation of the U-N bond is somewhat special. The discussion here is divided into two cases due to the discrepancy of the N3coordination patterns. The first one is the U-L1 bond length, which is the U-N bond length in [UO2N3]+, as summarized in Fig.4(b). The bond length variation of the U-L1 bond is not monotonic, which will be explained in the following discussion section. The second one is the dative bond between U and Ln whenn≥2. The pattern of action here is distinguished from the azido-metal bond of L1, instead in a dative character. This U-N bond length is named as U-L and is averaged here for convenience in the cases ofn=2, 3, and 4 each. The average U-L bond length variation is consistent with the U-N bond length variation in the [NUO(N2)]+system, as shown in Fig.4(c)[21]. This can be attributed to two reasons: (1) The unpaired electrons on N3radicals enter the empty f orbitals of U when the N3ligands are ligated, which leads to an increase in the populated electrons. These electrons may have a certain shielding effect, resulting in a reduced interaction between the U atom and the ligand. (2) As the ligand increases, the narrowing of the coordination space induces a steric effect, which also leads to the growth of the U-N bond.

3.4 NPA charge and NBO spin analyses

Table 1 The NPA charges for [UO2(N3)n]+(n=1-4) and isolate at B3LYP/VTZ-PP level

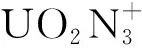
Table 2 The NBO spins for [UO2(N3)n]+(n=1-4) and isolate B3LYP/VTZ-PP level

3.5 Bond order, Kohn-Sham MO and natural localized valence MO(NLMO) analyses

We further carried out the bond order analyses for U-N bonds based on the Mayer, Wiberg and Fuzzy methods, as listed in Table 3. The results of Fuzzy method are much larger than other two methods. The U-O bond orders for all the complexes are in the region of 2-3. The bond orders of U1-N4are in the region of 1-2, implying that it is an azido-metal bond. The bond orders of another U-N bond(in L2, L3 and L4) are in the region of 0.5-1. The trend of change in bond order of U1-N4with the increase of coordination number is consistent with the tendency of the U1-N4bond length.

Table 3 The bond order calculation for [UO2(N3)n]+(n=1-4) and isolate B3LYP/VTZ-PP level

For a better understanding of the U-L bonding in [UO2(N3)n]+(n=1-4), the NLMO analyses are conducted. As shown in Table S7(See the CNKI enhancement document for details), for [UO2N3]+, the U-N bond is mainly composed of a 2-center σ-valence molecular orbital(13%U+86%N) and double 2-center π-valence molecular orbitals(14%U+73%N). For [UO2(N3)n]+(n=2-4), multi-center π-valence types orbitals are found, which also undergo delocalization among the ligands. In addition, the range of delocalization and the degree of delocalization of the multi-center π-valence orbitals have been changing continuously. This caught our attention and provided an explanation for the seemingly irregular variation of the U-L1 bond length mentioned above. According to the results of NLMO analyses, when the second N3is coordinated, the π orbitals originally located on U-N4 delocalized to the second ligand, forming a 3-centered delocalized system of N4-U1-N7(16%U1+47%N4+21%N7) with U-N4 percentage of 63%. It can be interpreted that U-N4 acts as a donor, and the π orbital electrons on the bond are delocalized to the π orbital of U-N7(L2) through the central uranium atom, which leads to a decrease of orbital electrons populated in the U-N4 bond, manifested by a weakening of the bond strength and an increase in the bond length. For [UO2N6]+, the extent of delocalization continues to spread into a 4-center system U1-N4-N7-N10(11%U1+73%N4+3%N7+3%N10), but the degree of delocalization at this point decreases instead, with the percentage of delocalized electrons in U-N4 rising back to 84% from 63% in [UO2N6]+. This leads to an increase in the density of the populated electrons on the U-N4 bond, exhibiting a shortening of the bond length. Finally, after the fourth N3coordination, the level of delocalization is greater with the delocalized electron fraction of U-N4 drops to 69%, causing another increase in bond length.

4 Conclusion

We provide the geometries of the experimentally obtained series of ions [UO2(N3)n]+(n=1-4) with the aid of theoretical calculations. The U-N bond length is used as a probe to investigate the effect of ligands. NPA charge and NBO spin analyses are also used to further elucidate the strength and properties of ligand-metal interactions. It is noteworthy that the multi-center π orbitals undergo different degrees and ranges of delocalization as the number of ligands increases, which is highly correlated with non-monotonic change of U-N bond length. A spatial interpretation of the coordination number CNeq=4 is also given. The experimental and computational results of this work enrich the actinide coordination chemistry and provide some preliminary theoretical bases for the uranyl complexes with N3as the ligand.

Expressone’sthanks: We would like to thank Prof. Weijun Zheng(Institute of Chemistry, Chinese Academy of Sciences) for providing us the NBO 7.0 software.