铀、钪族金属氮化碳配合物结构、成键和还原性质的密度泛函理论研究

安 然,孔 明,胡万权,倪义东,沈永鹏,李淑君,郭元茹,*,潘清江,*

1.东北林业大学 材料科学与工程学院, 黑龙江 哈尔滨 150040;2.黑龙江大学 化学化工与材料学院, 黑龙江 哈尔滨 150080

单原子催化剂由于其优异的催化性能而引起了科学工作者的广泛关注[1]。目前,已采用了多种方法,诸如构筑缺陷、负载金属和掺杂原子等[2-4],改性和调整催化剂的微观结构和电子性质。单原子催化剂可以获得最大的原子利用效率,提高催化活性和减少消耗;高度孤立的单个金属原子可以提供更多的活性中心来增强催化活性,从而促进多相催化的发展。

利用空间限域效应将金属原子或离子固定在具有配位作用的空穴中是制备单原子催化剂的有效策略之一。由于易于制备、成本低、电子结构匹配和配位空穴大小适当,石墨型氮化碳(g-C3N4)可以作为单原子催化剂的优良基质材料,并表现出优异的半导体光电催化活性[5-6]。最近,Gao等[7]发现g-C3N4负载Pd和Pt可以制备稳定的光催化剂,并对CO2还原具有很好的性能。Huang等[8]开发了g-C3N4负载Co单原子催化剂,实现了CO2的选择性还原。文献[9]合成了氮化碳纳米管支撑稀土Er单原子的复合材料,具有高效的光催化CO2性能。

基于这些研究,选择适当大小和电子结构匹配的金属或离子锚定在g-C3N4空穴中,对增强其催化活性具有重要的意义。在本工作中,理论设计g-C3N4(CN)负载系列U、Sc族金属离子,形成稳定的配合物[M(CN)]z+,其中金属M分别为Sc、Y、La、Ac和U,z分别为2和3。通过探索配合物几何和电子结构、配位空穴对金属离子的稳定化作用(成键)和单电子还原性质,以期对相关单原子催化剂合成与应用提供可靠理论支持。

1 计算细节

计算采用Priroda程序在气态和不使用任何对称性条件下优化配合物结构。运用标量相对论全电子(AE)哈密顿,并同时使用广义梯度近似的GGA-PBE(Perdew-Burke-Ernzerhof)[10]泛函和全电子Gaussian基组。以优化的结构为基础进行频率计算,结果未发现虚频,说明这些结构为势能面上的极小值点。计算还得到电子自旋密度、Mulliken电荷和Mayer键级。

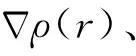
2 结果与讨论

2.1 几何结构

采用密度泛函(DFT)理论方法优化了g-C3N4配体结构单元,标记为CN。将三价和二价金属离子放置于配体空穴中,计算得到配合物[M(CN)]z+(M=Sc、Y、La、Ac和U;z=3和2)稳定结构。配体和代表性配合物示于图1,而优化的结构参数(键长、键角)、键级等列于表1。尽管有共轭存在,优化显示g-C3N4的各原子并不完全处于一个平面内,其三个3-s-三嗪结构单元相互交错。然而引入金属后,配体的平面性增强,其六个N供体原子近似在一个平面内,标记为N6。测量的M到N6平面键长(DM-N6)显示,[Sc(CN)]z+(z=3和2)的中心金属几乎位于N6平面内,对应的键长分别为0.003 Å(1 Å=0.1 nm)和0.004 Å(表1);其它金属均不在N6平面内,其中金属Ac偏离N6平面最远,DM-N6分别是0.959 Å和0.907 Å。相比较而言,金属相同时,[M(CN)]3+的中心金属比[M(CN)]2+的偏离N6平面更远些。另外,优化的N-M-N角(α)也支持这一结论:即,当α→60°时,金属位于平面内;偏离越大,金属偏离平面越远。因此,计算的[Ac(CN)]z+(z=3和2)的α角分别为55.5°和56.0°,偏离平面最远。当金属相同时,从z=3→2变化,即发生单电子还原时,Sc配合物的DM-N6基本保持不变(变化仅为0.001 Å),而其它四个金属时DM-N6则变短0.010～0.084 Å,这表明还原作用使得金属中心更趋近于N6平面。

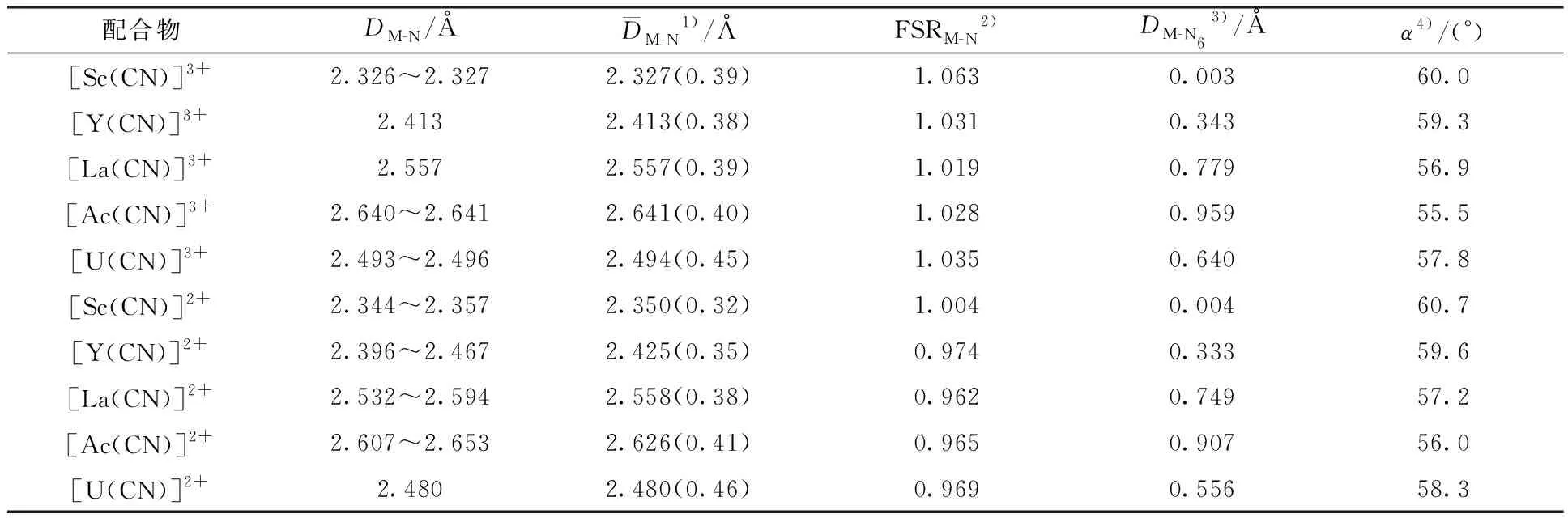
表1 计算得到的[M(CN)]z+的键长(D)、键角、键级(括号内数值)和FSRM-NTable 1 Optimized bond lengths, angles and bond orders(in parenthesis) of [M(CN)]z+, along with calculated formal shortness ratio(FSRM-N)

图1 研究的含六个N空穴的g-C3N4配体单元(CN)(a)和配合物[M(CN)]z+(M=Sc、Y、La、Ac和U;z=2和3) (b)的结构图Fig.1 Investigated structures of molecular unit of g-C3N4 containing six nitrogen donors(marked as CN)(a), and [M(CN)]z+ (M=Sc, Y, La, Ac and U; z=2 and 3)(b)

2.2 配体与金属相互作用

为了更好对比,将M-N键长相关的系列参数绘制于图2中。对于配合物[M(CN)]z+,从图2(a)可以看出,当带有三个正电荷(z=3)时,优化的M-N键长(平均值)先逐渐增长后缩短:即中心金属由Sc变到Ac,M-N键长是逐渐增长的,而从Ac到U的键长缩短;在Ac原子处出现拐点。同样的,当z=2时,M-N的键长变化趋势与z=3时一致,均为先增长后缩短,在Ac处出现拐点。[M(CN)]3+从Sc→Y→La→Ac键长增长与同族元素随着周期数增加原子半径增大相符合,而Ac→U的M-N键长缩短可归结为锕系收缩概念。

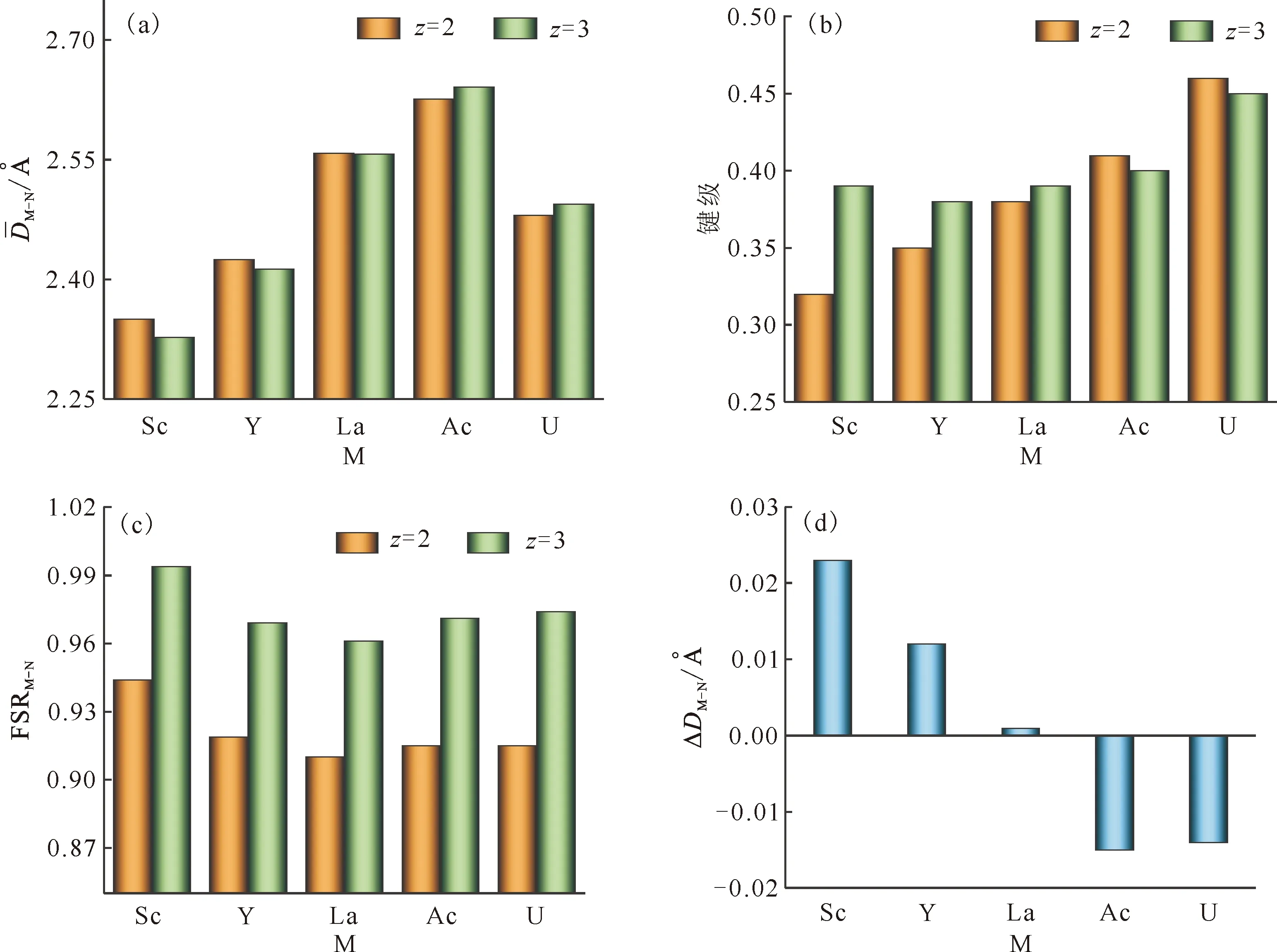
图2 计算的配合物[M(CN)]z+的M-N平均键长(a)、键级(b)、FSRM-N(c)和还原前后配合物M-N键长差(ΔDM-N)(d)Fig.2 Calculated distances of M-N(a), bond order(b) and formal shortness ratio FSRM-N(c) for [M(CN)]z+, along with difference of M-N distances between complexes before and after one-electron reduction(d)

由图2(a)还发现,二价配合物阳离子(z=2)的M-N(M=Sc和Y)的键长要稍长于三价配合物(z=3)的。而有趣的是,随着中心金属原子序数增加,二价阳离子配合物的M-N键长逐渐与三价的相接近,最后二价的M-N键长变得比三价的短。出现拐点的位置同样是在Ac处。为了进一步考查金属和配体作用,绘制M-N键级示于图2(b)。由图2(b)可以看出,当z=3时,随着中心金属原子序数的增大,键级的趋势是先减小后增大的,总体变化趋势是上升的;当z=2时,键级的变化趋势为单调递增的。比较z=3和2时的键级发现,在M为Sc、Y和La的时候,三价配合物的M-N键级高于二价的;当中心金属为Ac和U时,则是三价配合物的M-N键级低于二价的。与图2(a)中M-N键长出现拐点的位置相同。

一般来说,键级大时,表明形成的化学键作用越强,而且相应的键长则是越短的。对比图2(a)和图2(b)可以看出,在M=Sc、Y、La时,三价配合物的M-N键级大于二价的,相应三价配合物的键长应该是短于二价的;而M=Ac、U时则规律相反。

在应用M-N键长比较化学键强度时,会因为原子半径不同造成比较困难。因此,引入了FSRM-N扣除原子半径不同的影响。从图2(c)可以看出,三价配合物的FSRM-N高于二价的。这与键长相反,和键级的情形相一致。同时发现,在La之后,FSRM-N趋于升高,与图2(a)和图2(b)中出现拐点的位置略有不同。在中心金属原子相同时,考虑[M(CN)]3+→[M(CN)]2+单电子还原对键长的影响,对二价和三价阳离子配合物的M-N键长进行了做差处理,得到还原前后配合物M-N键长差(ΔDM-N)示于图2(d)。由图2(d)可以看出,在这五种配合物的还原过程中,M-N键长的变化值较小。当M=Sc、Y、La时,还原作用使得M-N键长增长,即还原作用使得金属和配体作用减小;而当M=Ac、U时,还原作用使得M-N键长变短。M(Ⅲ)的离子半径小于M(Ⅱ),所以结合ΔDM-N结果,可以粗略判断,Sc、Y和La配合物的单电子还原有可能发生在金属中心,而Ac和U配合物的单电子还原更可能发生在配体。

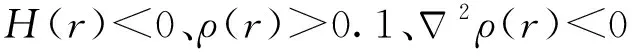
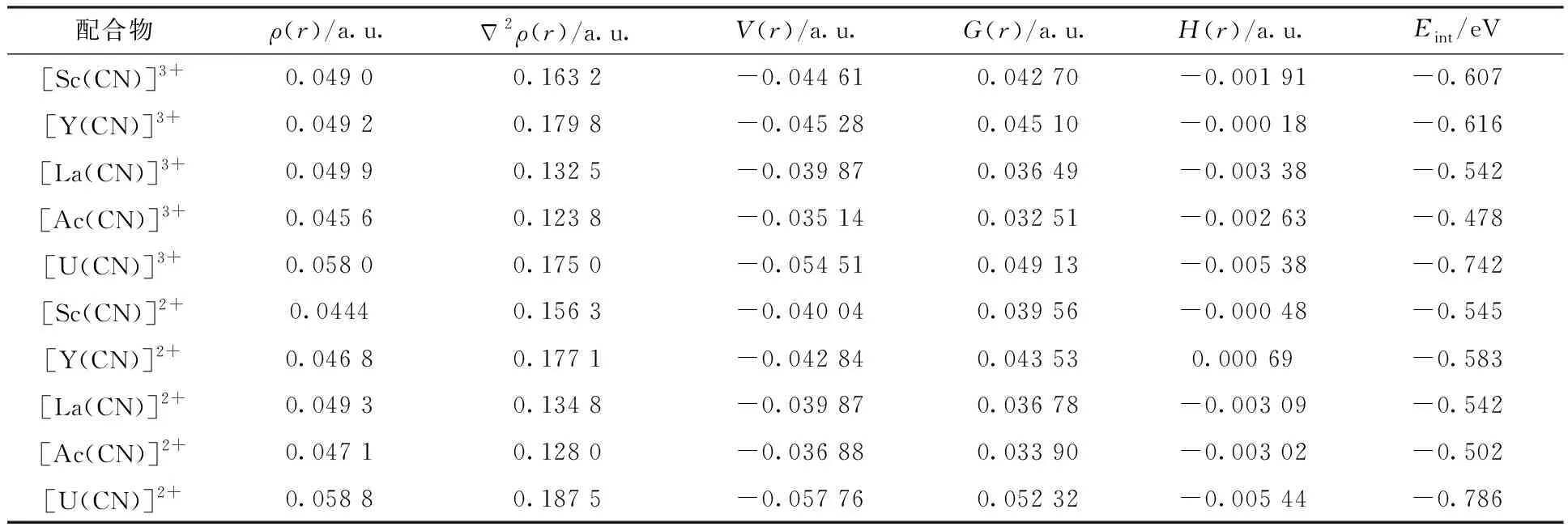
表2 配合物[M(CN)]z+在M-N键临界点的QTAIM参数和键相互作用能EintTable 2 Calculated QTAIM data at M-N bond critical points(BCPs) of [M(CN)]z+, together with bond interaction energy Eint

2.3 单电子还原与电子结构

计算的配合物[M(CN)]z+(M=Sc、Y、La、Ac和U;z=3和2)各片段的电子自旋密度(S)与电荷(Q)列于表3。通过这些计算结果,一方面可以判断中心金属在单电子还原前后的氧化态,另一方面,帮助分析各部分之间的相互作用,并与键长、键级和QTAIM参数相印证。当中心金属M为二价时,Sc、Y、La和Ac离子的电子自旋密度理论期望值为1.0,而U(Ⅱ)的为4.0。当中心金属M为三价时,U(Ⅲ)离子的电子自旋密度理论期望值为3.0,其它M(Ⅲ)的均为0.0。根据表3数据,可以看出[M(CN)]2+中心金属如果为二价,计算的中心金属的电子自旋密度SM均小于期望值,而配合物中配体的SCN大于0。这说明有部分电子从金属转移到了配体上,且在Sc族中随着原子序数的增加,电子自旋逐渐偏离期望值。当中心金属为Ac原子时,发生的电子流向最为明显。这说明Ac应该为Ⅲ价。对于[M(CN)]3+系列配合物,中心金属SM的计算值与M(Ⅲ)期望值相符,几乎没有发生电子转移。

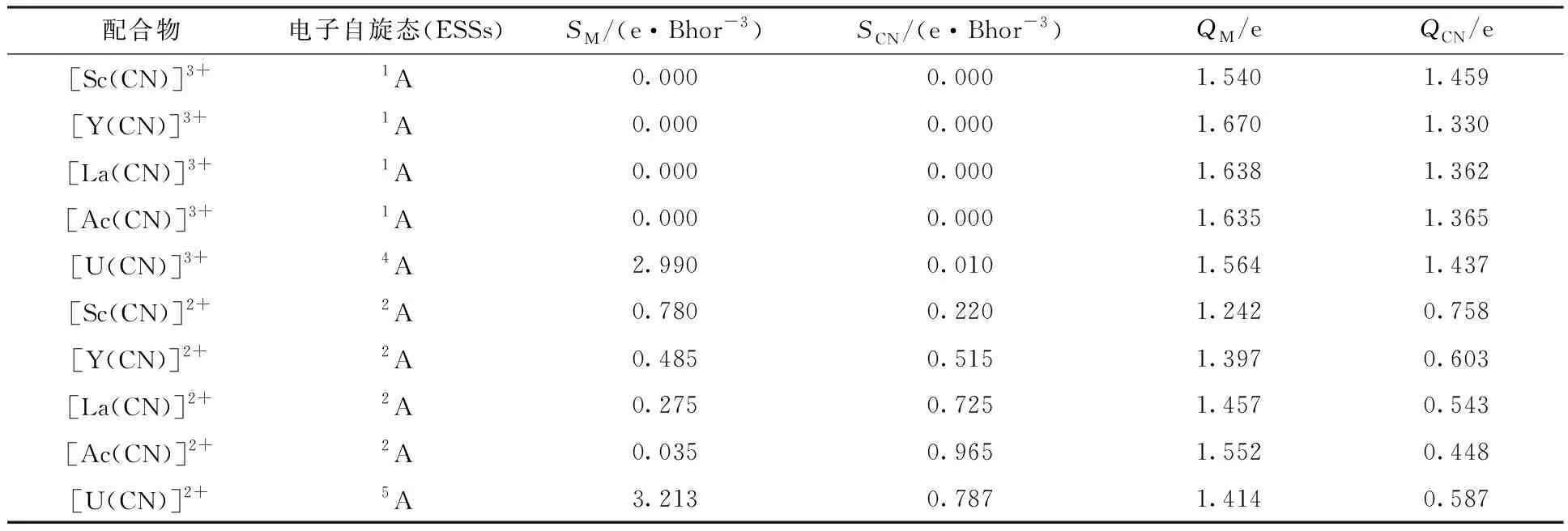
表3 [M(CN)]z+的金属和配体片段的电子自旋密度和电荷Table 3 Electron-spin density and charge of each fragment for [M(CN)]z+

进一步考察[M(CN)]3+单电子还原生成[M(CN)]2+过程中各组分的自旋密度变化ΔS,结果示于图3。如图3所示,当M为Sc时,发生单电子还原时,金属捕获的电子相对较多,而配体部分捕获的电子相对较少;这说明在还原时,金属与配体均参与了反应,且金属Sc起主导作用,可以认为三价Sc还原为二价。当中心金属为Y时,ΔSM为0.485,而ΔSCN为0.515,金属和配体同时被还原。在中心金属为La和U时,单电子还原主要发生在配体上,对应的ΔSCN值分别为0.725和0.777。而当中心金属为Ac时,是发生配体还原,金属部分仅捕获0.035的电子。

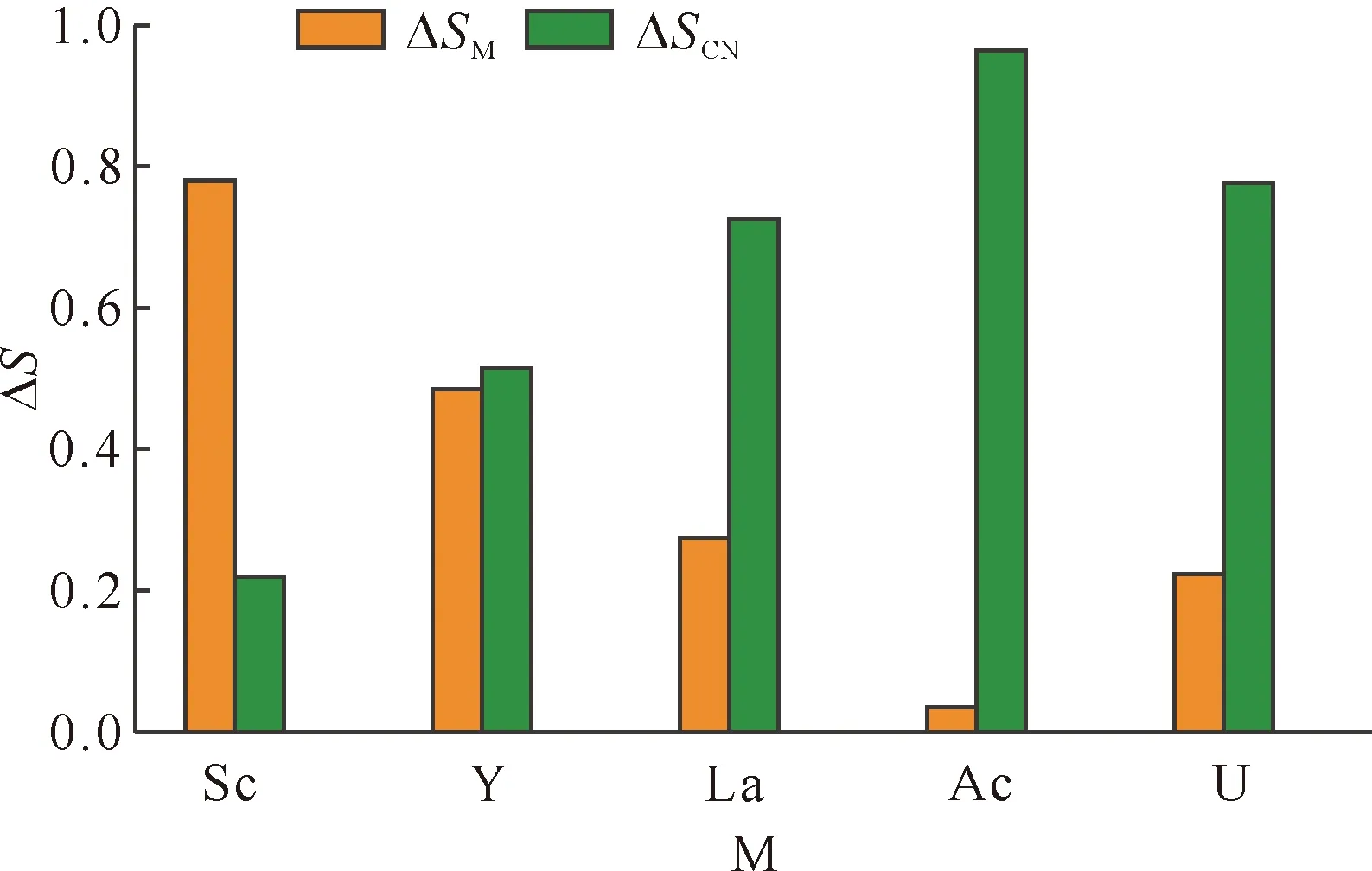
图3 配合物[M(CN)]3+单电子还原为[M(CN)]2+过程中金属和配体片段的自旋密度变化ΔSFig.3 ΔS value of each fragment while reducing [M(CN)]3+ to [M(CN)]2+ by one electron

为了解析配合物电子结构,绘制了[U(CN)]z+(z=3和2)的α自旋轨道态密度(DOS)和电子云图,结果示于图4和图5,并将部分前线轨道成分列于表4和表5。对于[U(CN)]3+,由图4和表4可以看出,其HOMO、H-1和H-2为金属U的轨道性质,5f分别约贡献86.7%、86.5%和93.7%,U(7s)和U(6d)贡献很少;这些轨道中没有CN的贡献。[U(CN)]3+中有三个自旋平行5f电子,U为Ⅲ价,与其计算的SM≈2.99相符合。该配合物的H-4为配体贡献轨道,为π(CN)性质。其低能的非占据轨道LUMO、L+1和L+2均由U(5f)组成,贡献超过92.6%。当发生单电子还原生成[U(CN)]2+时,由图5和表5可以看到,出现了四个U(5f)为主的轨道,即HOMO—H-3,其中HOMO和H-1的5f成分超过74.6%,而在H-2和H-3中,金属贡献约为50%～60%。值得指出的是,在H-1、H-2和H-3中配体CN的贡献分别约为2.3%、28.9%和17.9%;如果把这三个轨道的金属和配体成分进行归一化处理,发现CN成分总和约为60%。这说明[U(CN)]3+→[U(CN)]2+的金属和配体均发生了还原,且主要发生在配体上。这与上面的电子自旋密度分析结论相一致。

表4 计算的配合物[U(CN)]3+的轨道成分分布(P)Table 4 Contribution of orbitals for [U(CN)]3+

表5 计算的配合物[U(CN)]2+的轨道成分分布Table 5 Contribution of orbitals for [U(CN)]2+

图4 配合物[U(CN)]3+的α自旋轨道态密度和电子云图Fig.4 Density of states of α-spin orbitals of [U(CN)]3+ and electron-density diagrams

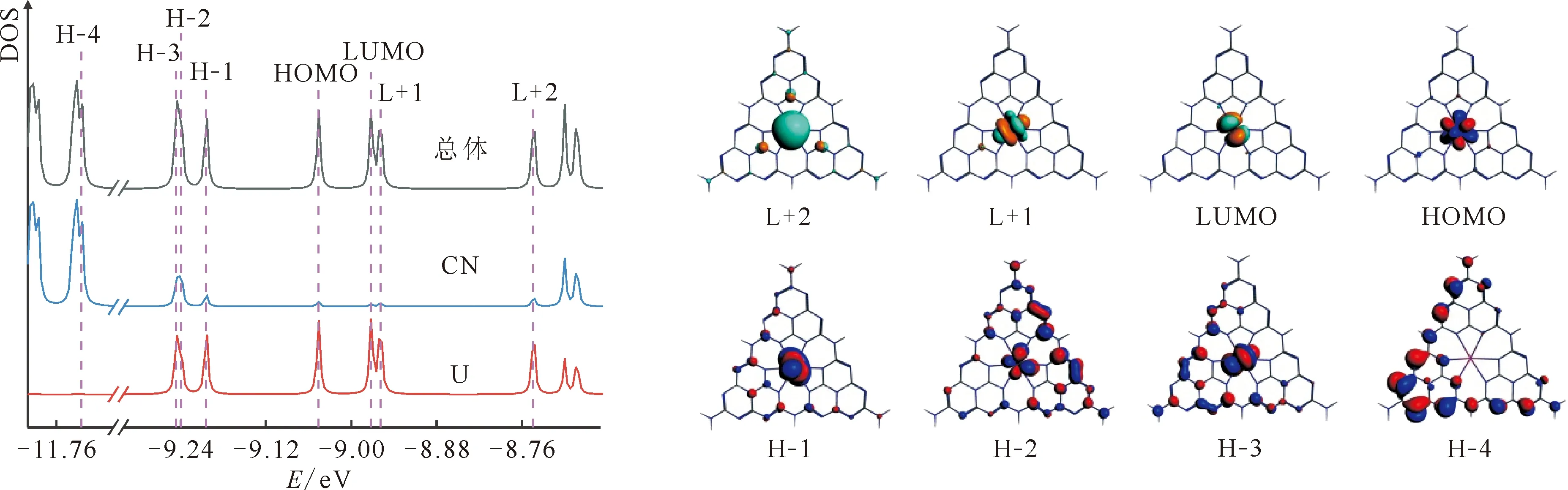
图5 配合物[U(CN)]2+的α自旋轨道态密度和电子云图Fig.5 Density of states of α-spin orbitals of [U(CN)]2+ and electron-density diagrams

3 结 论

采用相对论密度泛函理论探索了氮化碳对系列金属离子负载和稳定化作用,系统研究了生成的配合物[M(CN)]z+(M=Sc、Y、La、Ac和U;z=2和3)的结构、成键和还原性质,得到如下结论:

(1) M-N键长随着原子序数增加的变化趋势为先增加后减小,并且发现对应的键级也增大;值得注意的是,这一研究结果不同于一般的常规认识,即键长和键级具有反比关联性;

(2) 不同中心金属配合物的被还原片段有很大差异:在M为Sc时,还原作用主要发生在金属部分,配体仅有极少的参与;而Y配合物则是金属和配体均参与,且占比相近;La和U配合物是金属修饰的配体还原机制;不同的是,Ac配合物的还原反应完全发生在配体上,金属未参与;

(3) 结合电子结构计算,指认[U(CN)]3+的中心U为三价氧化态,而[U(CN)]2+的U则介于三价和二价之间;计算发现配合物为M-N6配位模式,N→M配位键强度值约在-0.47～-0.79 eV范围。

总之,g-C3N4可以通过其N6配位空穴负载金属原子,从而形成单原子催化剂。计算得到的几何/电子结构信息、化学键和氧化还原性质等将为氮化碳基金属单原子催化剂的合成与应用提供准确的理论依据。