海水声速模型研究进展及南海声速模型展望

彭莉虹, 张宝金,2, 顾 元,2, 李 延,2, 马金凤,2, 耿明会,2

(1. 南方海洋科学与工程广东省实验室(广州), 广东 广州 511458;2. 广州海洋地质调查局 自然资源部海底矿产资源重点实验室, 广东 广州 510760)

0 引 言

海水声速具有三维和随机时变的特点，无论是利用观测手段还是利用理论手段，研究海水声速的时空变化都极具挑战性[1]。声速是海水特征研究的经典问题，声速测量也服务于海洋工程的广泛需求。目前海水声速主要通过2种方法进行测量：一是声速仪直接测量法，二是经验公式间接计算法[2]。直接测量法是通过声波在固定路程的传播时间或波长与频率的关系，直接获得声波传播速度的方法；间接测量法基于温度、盐度等参数计算声速[3]。除了传统的直接和间接测量法外，一些新型声速测量方法也正在发展，如地震海洋学方法[4]，但尚未广泛应用于声速研究。

直接测量法虽然精度高，但观测范围有限。间接测量声速，进而构建海洋水体声速模型，在描述大范围海域、模拟真实海洋三维的声环境时具有显著优势。海水声速模型已成为声速研究和应用的重要方向，本文阐述海水声速模型的构建类型，总结全球海水声速模型的研究进展，并以南海为切入点，展望南海声速模型，以助于揭示海水声速的空间变化规律，深化海水声速在不同领域的应用效果。

1 海水声速模型研究进展

按照模型构建方式可将海水声速模型分为数学模型和数值模型。

1.1 数学模型

数学模型使用参数化的数学等式(如解析函数表达式)描述声速结构。

在流体介质中，声波是弹性纵波，纵波声速c可表达为

(1)

式中：ρ为流体密度；β为绝热压缩系数。ρ与β都可以是温度、盐度和压力的函数，因此可推出海水中的声速是温度、盐度和静压力的函数。但用式(1)完整地解析表达声速比较困难，通常采用经验公式进行计算。

从20世纪50年代开始，学者们先后提出一系列声速经验公式，将声速总结为温度、盐度和深度(或压力)等参数的函数。当前海水声速经验公式的更新主要通过声速校正的方式开展，进而提高声速测量精度[5]。常用的经验公式包括 Wilson式、Leroy式、Frye和Pugh式、Del Grosso式、Medwin式、Chen-Millero式、Mackenzie式、Coppens式、Chen-Millero-Li式等[6]。在进行海洋调查时，国际上主要使用Wilson式、Chen-Millero式(Chen-Millero-Li式)和Del Grosso式等，国内一般使用Chen-Millero式[7]。

Chen-Millero式适用范围为0≤T(温度)≤40 ℃，5 ppt≤S(盐度)≤40 ppt(注：ppt可指ng/L或ng/kg)，0≤P(压力)≤1 000 bar(1 bar=0.1 MPa)，具体表达式为

V=Vw(T，P)+A(T，P)S+
B(T，P)S3/2+D(P)S2

(2)

式中：Vw(T，P)为纯水中的声速；A(T，P)=1.389-1.262×10-2T+7.164×10-5T2+2.006×10-6T3-3.21 ×10-8T4+(9.474 2×10-5-1.258 0×10-5T- 6.488 5×10-8T2+1.050 7×10-8T3-2.012 2×10-10T4)P+(-3.906 4×10-7+9.104 1×10-9T-1.600 2×10-10T2+7.988×10-12T3)P2+(1.100×10-10+6.649×10-12T-3.389×10-13T2)·P3；B(T，P)=-1.922×10-2-4.42×10-5T+(7.363 7×10-5+1.794 5×10-7T)P；D(P)=1.727×10-3-7.983 6×10-6P。

各声速经验公式的复杂程度不同，适用条件不同[8]，限于篇幅不一一列明。

在声速的深入研究中，Munk模型[1]和GDEM(Generalized Digital Environmental Model)[9]作为经典模型被广泛应用。Munk模型用指数表达式表示中深纬度深海海区的声速，已受到普遍认可。基于Munk模型简化声速剖面，构建线性声速分布模型，已获得较高精度的深海水体声速模型[10]。GDEM是用于保障美国海军声呐使用的数字环境模式，可用于计算海域声速。

1.2 数值模型

随着建模理论和数值模拟方法的进步，学者们采用计算机计算和图像显示等模拟技术，通过拟合或插值、反演，重构多层次的网格数据，构建海洋水体声速的数值模型，形成高空间分辨率的声速描述[11]。

数值模型的典型代表为经验正交函数(Empirical Orthogonal Function，EOF)模型[12]。EOF可分解产生基函数，通过选取高阶数，实现声速的高精度拟合，近似表示声速剖面[13]。孙文舟等[14]将EOF应用于简化声速模型。孙文川等[15]将EOF用于多波束数据处理，对声速剖面数据进行修正，提高了勘测效率和精度，改正了声速误差引起的海底地形失真。张孝首等[13]利用温盐深剖面仪(Conductivity，Temperature，Depth，CTD)实测数据，基于EOF方法实现深海5 000 m全深度声速剖面场的重构。

全球观测系统和数据集的搭建为声速模型的构建提供了范围更广、尺度更大的可靠温盐数据，如自沉浮式剖面探测Argo浮标[16]、全球海洋图集(World Ocean Atlas，WOA)[17]、美国海洋数据同化系统(Modular Ocean Data Assimilation System，MODAS)[18]等。通过全球观测系统间接获得声速，是声速数值模型构建的重要数据基础[19]，也实现了较好的应用效果。MODAS提供高分辨率三维网格温度场和盐度场，也被用来产生海水声速场，结合MODAS与EOF可减少计算量，提高声速模型的重构精度[18]。Argo浮标通过实地测量海水上层的温度、盐度的剖面数据研究海洋的变化，全球大概有超过4 000个Argo浮标漂浮在各大洋，实时提供温盐剖面数据[16]。徐寿志[19]、李洪超等[20]基于Argo浮标数据重构精度较高的区域海水声速模型。蔡艳辉等[21]基于Argo浮标的剖面数据，提出一种基于经验正交函数原理和面球谐函数展开的全球三维声速场的方法。CHEN等[22]提出在温盐稳定的深海利用Argo的数据，可重建全球海水声速剖面(见图1)。WOA可查询任意经纬度的各个海洋参数，汇集全球海洋的主要海洋参数场，包括现场温度、盐度等历史统计资料。黄辰虎等[23]利用WOA 2018历史温盐信息，并结合不同类型设备的观测资料，构建全深度声速剖面。张启国等[24]对WOA 2013温、盐预测的声速剖面与CTD实测数据进行对比，计算结果的整体符合性较好。吴开明等[25]引入高精度全球海底地形和WOA声速剖面场为环境背景，建立全球海洋声场预报系统。当前，由海洋表面卫星遥感数据外推海洋水体的结构成为新的研究热点[26]。通过卫星遥感的海洋表面高度、温度数值外推，进而获得水下参数，也有望成为构建水体声速数值模型的新方法[27]。

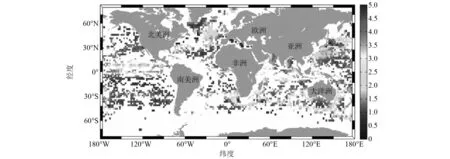
图1 根据Argo数据重构的声速剖面异常图[22](在每个2°×2°经纬度网格中，平均气候学分析与Argo剖面获得的声速剖面异常的差值)

1.3 声速模型的区别和联系

选择第1.1节和第1.2节的代表性模型，将其特征进行对比，如表1所示。

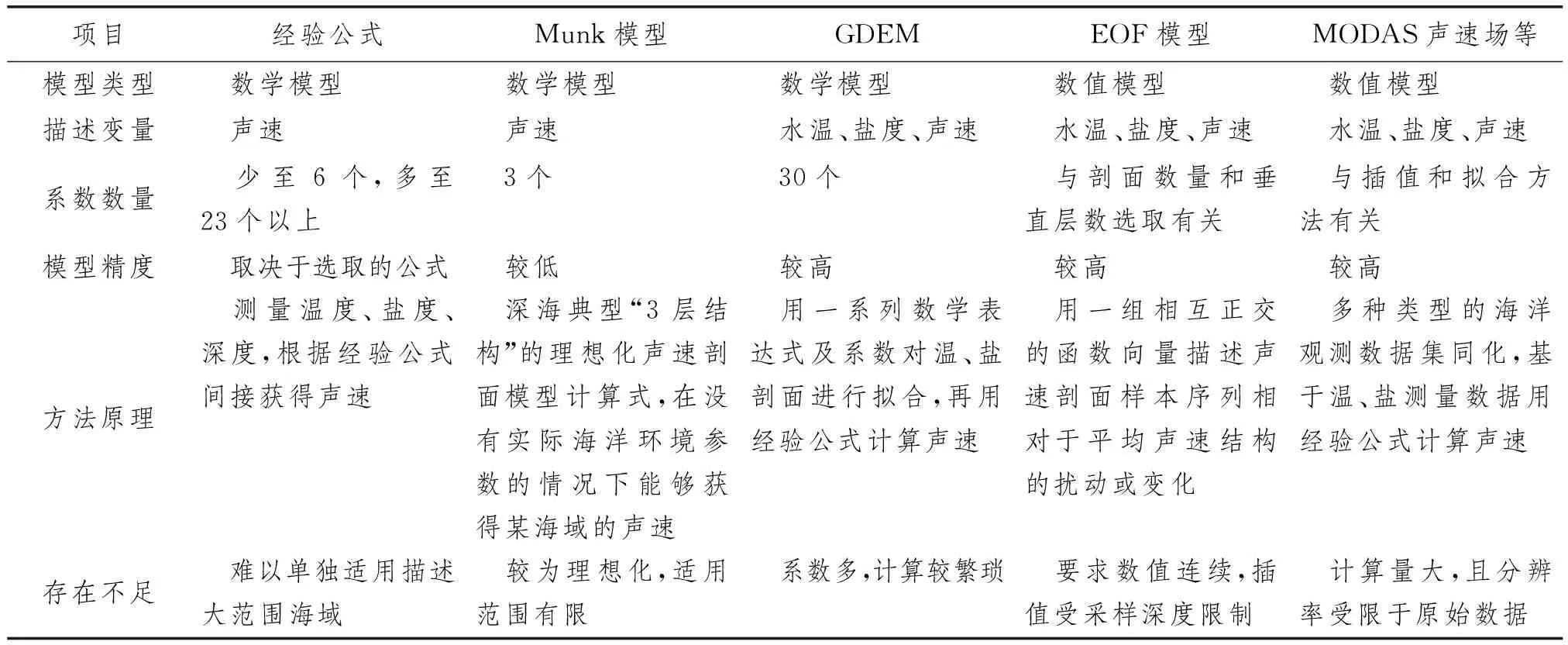
表1 几种声速模型比较

在数学模型中，经验公式是目前获得海水声速的普遍方法，但各公式适用条件不同，难以单独适用描述大范围海域，在模拟真实海洋三维声环境时，常与其他拟合方法结合。Munk模型适用于中纬度深海海区的声速，但其较为理想化，适用范围不广。GDEM对不同海域的真实海洋环境更具有广泛的适用性，但计算较繁琐。

数学模型具有良好的拓展性，但结构过于理想，且大多参数被用来构造温盐结构，对描述声速的直观意义不大。在此基础上发展的数值模型可达到较高的声速拟合精度。EOF 模型为典型代表，但其局限在于：测量数据在空间上必须是连续的，否则需要插值，也受到样本采样深度的限制。以MODAS声速场为代表的各种声速模型可基于大量观测数据得到较高分辨率的宏观模型，但也相应地要求巨大的计算量，且分辨率受限于原始数据。

各种声速模型并非互相孤立，而是相辅相成的。海水声速直接测量的情况较少，大多通过经验公式间接获得。经验公式数学模型为其他大部分声速模型提供数据基础；采用数值模型对稀疏的声速数据进行重构，可为三维声速模型的研究提供数据支持。

2 南海声速模型展望

作为我国重要的边缘海，南海海底地形多变，声速分布特性复杂，且缺乏长期连续观测资料[28]。南海声速模型有巨大的研究价值及应用需要，对于水体信息研究、多波束测深、高精度水声定位、地震成像与解释等都有重要意义，亟须进一步发展。

2.1 研究需要

2.1.1 南海声速时空分布特征复杂

南海面积约350万km2，呈长轴为东北-西南走向的半封闭菱形。海底地势西北高，中部和东南低。复杂的海底地势使南海声速分布具有特殊性，南海声速具有复杂的时空分布特征，构建声速模型可对其进行准确的描述。

南海声速具有区域性和季节性变化特征。按水深可将南海声速划分为3种类型，南海中部属于深海型声速剖面，南海北部的陆架区域属于浅海型声速剖面，南海南部属于过渡型声速剖面，如图2[14]所示。实测的南海全海深声速剖面体现出深海型特征，声道轴深度约 1 150 m，最小声速为1 484 m/s，海底附近海水声速(1 533 m/s)小于海面处海水声速(1 541 m/s)[29]。南海中部的表层和次表层声速有复杂的区域性和季节性变化：次表层以下结构较为稳定，呈现出“主跃层+深海声道轴+深海正梯度”的结构；在南海北部陆架，在春、夏、秋三季，海区呈现“混合层+季节性跃层+下均匀层”的结构，冬季为均匀型结构[30]。

图2 典型海水声速剖面示例

2.1.2 南海声速影响因素繁多

海水声速与海洋环境高度相关，除了温度、盐度、深度的影响外，不同尺度的海洋物理现象也会对声速造成影响。南海声速的垂直分布受海水升温和降温的影响显著，季节变化主要由盐度和海流差异引起[31]，构建声速模型可更好地量化各因素的影响。

水温和盐度是影响声速的重要参数，海水中声速的影响规律如下：温度每增加1 ℃，声速增加约4.15 m/s；盐度每变化1‰，声速变化约1.13 m/s；深度每增加1 m，压力增加约10.1个大气压，声速增加约0.16 m/s[21]。南海北部声速的分布和温度的等值线类似，说明该海区声速受温度的影响较大[32]。南海表层与深层声速分布明显不同，表层声速受海水温度变化影响大，深层声速与环流密切相关[33]。

在大尺度海流(黑潮)峰区内，声速、温度、盐度、密度都有强烈的变化。南海东北部海区存在明显的黑潮水入侵南海现象[34]。CHEN等[35]通过分析黑潮延伸区域的Argo数据和海面高度数据，建立二维声速特征模型和三维声速环境，表明黑潮延伸区域主要改变声道深度。

南海环流场呈现多涡结构，由于中尺度涡旋与周围水体存在温度差异，会引起相应的声速分布和声传播条件变化，导致南海涡旋区声速存在复杂的结构[36]。中尺度涡扰动声速场，暖涡使声波辐散，冷涡使声波辐聚[37]。中尺度涡能改变声速梯度(正梯度或负梯度)[37]，冷涡的存在会引起声速场的低值中心[28]。内波等动力学过程会造成声场强度的起伏[38]，可引起三维声场效应[39]。内孤立波在南海北部广泛存在，ZHAO等[40]通过反向回波测深仪在南海西北部观测到内波。小尺度湍流也会使水体出现声波起伏，模拟小尺度海洋现象对海洋声学层析成像反演计算至关重要[41]。

2.2 满足应用需求

2.2.1 多波束测量声速校正

高精度多波束测量结果可在南海的水深测量、海底地形描绘[42]和海洋地质灾害研究[43]等方面发挥重要作用。多波束测深系统的测量数据在很大程度上依赖于海水声速，声速的准确性直接影响多波束测深系统测量结果的精度和可靠性，准确的声速模型可校正多波束勘测水深的误差[44]，得到高精度的结果。

2.2.2 海洋精密水声定位

高精度水声定位是目前及未来海底测地的主要技术手段[45]。高精度水声定位系统对南海水声定位的军事需求提供可靠的科学依据，并在南海科学考察及矿产勘探得到应用[46]。随着海洋声学设备的发展，高精度水声定位的制约因素正逐渐从硬件设备的测量误差转变为理论方法的不成熟，尤其是海洋环境的动态变化及其造成的声速模型误差[47]。声速的误差直接影响水声距离定位结果，海水声速梯度直接影响声线的准确性[19]，水声定位系统的声速校正对高精度定位起着重要作用[48]。

2.2.3 海洋水声通信

南海深海自然资源勘探、南海水下安全维护都离不开海洋水声通信技术[49]。水下无线通信首选的载体是声波，目前远距离通信主要依赖于水声[50]。对南海水体声速模型进行深入研究，有助于学者们认知水声传播规律，改进水声通信技术。

2.2.4 地震深度域成像

南海区域构造复杂，增加了地震成像和解释的难度[51]。深度域速度模型的精度是地震偏移成像质量的决定因素之一[52]。韩复兴等[53]针对南海中深层水体的偏移成像问题，阐释海水声速模型对偏移成像质量有重要影响。准确的南海声速模型是实现高精度地震深度域成像的良好基础。

2.2.5 海洋水体特性研究

通过声场反演方法[54]，学者可深度研究南海水体的物理特征及物理过程。QU等[55]通过声速剖面的反演获得南海的内波信息。CHHUN等[56]用自动声速拾取分析方法对多道地震反射资料进行分析，直观地反映黑潮精细尺度的温盐结构和声速剖面的时空变化，为研究海洋学过程以及大规模海流和气候系统提供参考。

2.3 发展方向

2.3.1 高精度宏观三维声速模型

南海声速模型多数为局部海域研究，缺乏高精度的宏观声速模型，研究空白有待填补。

南海的声速研究早期发端于区域海洋调查。学者们根据国家《海洋调查规范》，用经验公式将调查数据换算为声速，分析声速分布特征[32]。近年来，EOF被广泛应用于南海声速模型的构建。张伟涛等[28]利用Argo剖面序列，通过EOF分析，分析南海北部海域声速垂直结构的时空变化特征和声速场水平分布特征。叶思雨等[57]优化南海北部内波活动下的声速剖面重构方法。陈小宇[58]融合多源数据，提出基于分布式测量的水体声速场高分辨率估计方法，并利用南海海试数据进行验证。基于全球观测系统，学者们也建立理论的声速数值模型。王文杰等[31]利用50年SODA系统月平均温、盐资料研究南海声速跃层时空分布特征，得到深度间隔为1 m的声速序列。HUANG等[59]利用2010—2020年的Argo数据重建南海声速场。ZHANG等[60]提出一种三维区域海洋要素场重构方法，针对南海北部的研究区域构建三维区域海洋温度和盐度场，实现较高精度的三维模型构建，但并未对声速场展开研究。

海洋环境是复杂的、动态的三维环境[61]，构建高精度宏观三维声速模型可更真实形象地表达复杂的海洋水体[62]，从而更准确地理解真实海域中海洋水体的声速情况。

2.3.2 动态预报宏观声速模型

海洋水体的声速研究并非孤立的单参数研究，在多参数影响下，准确描述声速的时空分布及进行动态预测将成为新的挑战。构建准确的动态预报声速模型可能是未来的重要方向，在给定南海全域指定坐标及时间的情况下，实现海水声速及声环境因素预测，乃至通过反演对内孤立波等海洋学过程进行预报。胡军等[63]采用2006—2017年我国南海部分区域Argo观测数据，建立反演预测模型，可用于垂直声速剖面的实时预测。HUANG等[64]根据2009—2012年南海部分区域CTD观测数据，建立南海声速场，可用于海水水体垂直声速实时预测。苏林等[65]基于内波统计特性，将声速剖面的预报问题简化为单一参数的时间序列预测问题，在南海试验数据上取得良好效果。

2.3.3 声速模型应用不断深入

以多波束水深测量声速校正、精密水下定位、水声通信、海洋物理特征研究等不同应用方向为目标，学者们对声速研究的侧重不同，实际应用需求将反推声速研究的发展。南海海水声速模型的应用将在不同领域不断发展，发挥更关键的作用。

3 结 论

声速是海水环境的重要参数。通过观测手段的发展和研究数据的累积，南海海水声速模型研究以声速经验公式、解析函数模型及经验正交函数模型为代表，由数学模型发展到数值模型。各种声速模型并非互相孤立，而是相辅相成的。

目前南海声速模型研究存在迫切需求，但南海全域的高精度宏观三维声速模型仍未成熟，对南海声速特征的研究以局域为主。可以预想，南海三维声速模型将在高精度宏观三维声速模型、动态预报宏观声速模型的方向上，逐步深化应用领域，取得新的进步。