基于候车时间和效益损失的城轨列车运行计划优化

张正坤，朱昌锋，景云，邢进

(1.兰州交通大学，a.交通运输学院，b.高原铁路运输智慧管控铁路行业重点实验室，兰州 730070；2.北京交通大学，交通运输学院，北京 100044；3.南京地铁运营有限责任公司，南京 210000)

0 引言

城市轨道交通(城轨)凭借正点、快捷及舒适等优势成为城市公共交通中的重要组成部分。城市轨道交通是各部门相互协同的复杂系统，为了给乘客出行提供优质服务，城轨列车按预先制定的运行计划运营，包括开行方案、时刻表及周转方案等。因此，制定符合客流需求和设备能力的运行计划对乘客和企业双方具有重要意义。

针对城轨列车运行计划，部分研究是在既定停站方案、运行交路及编组数量等信息的情况下，根据沿线各站的客流需求，利用数学规划等方法优化列车时刻表，并在此基础上进一步确定列车的接续方案[1]。这种逐步递进的研究策略分解了问题的复杂性，但也忽略了时刻表与接续方案的相互协同，使上下行列车在车底数量受限时有可能出现接续失败的情况[2]。为此，史峰等[3]通过耦合时变客流与发车时间，构建列车时刻表和接续方案的数学优化模型，并设计了双向关联序列化算法和匈牙利算法；WANG 等[4]通过分析列车折返与进出场环节的内在关联，提出时刻表与周转方案集成优化的多目标非线性混合整数规划模型；YUE等[5]从耦合时刻表与接续方案的角度，建立两者的双层规模模型，该模型采用模拟退火算法求解。整体优化策略能够有效确保系统的全局最优性，但上述研究仅以一端设有车场的城轨线路为背景，其研究成果不能适用于两端各设车场的城轨线路。

相对而言，线路两端各设车场能够有效减少列车进出车场的空驶距离，从而为开行匹配客流需求的不成对列车提供保障。针对线路两端各设车场的运行计划，张京辉等[6]从列车数量受限角度构建数学优化模型，模型求解采用NSGA II(Non-dominated Sorting Genetic Algorithm II)算法；李纵然等[7]考虑高峰时段各方向客流需求差异较大等因素，研究非主客流方向上开行快慢车的运行计划，提高主客流方向的发车频率；ZHAO等[8]从多编组技术角度研究该问题。列车接续是确保运行计划顺利实施的关键，面对两端各设车场的城轨线路，列车接续环节比较复杂，模型刻画存在困难。针对该问题，上述研究采用终到列车立即折返或入场待令的接续策略，降低模型建立和求解的难度，但却忽略了返线存车能力限制以及由此导致的列车接续决策，使优化得到的结果与实际过程不符，有待进一步完善。

候车时间是影响乘客出行时间成本的主要因素，是编制城轨列车运行计划需要关注的重点[9]。为兼顾车内舒适性及列车利用率，部分学者还考虑了列车满载率的均衡性[10]，但满载率仅是载客人数与列车载客能力的比值，虽能体现列车内载客状态，却不能反映该状态在运行区间的持续效应，且量纲与候车时间存在较大差异，不便于方案决策和分析。为弥补上述不足，本文引入运营效益概念，即运营企业根据客票收入、资源投入、运营安全及舒适度评价等因素对列车载客状态及时间持续做出的益损比较。显然，过少的载客量将造成资源浪费和影响运营收入，而过多的载客量又将容易产生安全隐患和降低服务质量。因此，在列车运行过程中，列车载客过多或过少均导致企业效益受损，且损失程度与载客状态的持续时间存在正相关性，而鲜有研究考虑此类问题。

综上，本文将导致运营效益受损的列车载客人数与其区间运行时间的乘积定义为效益损失。在此基础上，引入关于列车始发和终到时间的状态变量，刻画折返站能力受限下的列车接续及进出场环节，强化研究的实用性。特别地，为兼顾运营效益，考虑到断面客流的不同需求导致运行区间效益损失的个体差异及其不可避免性，引入调控因子调控决策效益损失的受重视程度，进而以候车时间和效益损失的上确界为优化目标，建立两端配有车场的城轨列车运行计划优化模型，并结合模型特性设计GA(Genetic Algorithm)-Gurobi的混合求解策略。

1 问题描述

在m个车站的城轨线路上，记Sf={1,2,3,…,m} 为f∈F={0,1} 方向依次编号的车站集合，Qf={1,2,3,…,m-1} 为区间集合，f=0为上行，f=1 为下行。对于s、s′∈Sf，若s=1，s′=m，则s和s′分别表示f方向上配有车场和折返线的首发站和终点站。设Mf为f方向首发站车场可提供的列车数，Nf为终点站折返线的最大存车能力，为折返时间，δl′,l,f为表示列车接续的0-1决策变量。运营过程中，若终点站存车需求大于Nf，则多余列车需存放至该端车场待避，Δtf为进出场时间。

设T1为运营开始时间，T2为结束时间，Df={1,2,3,…,|Df|}为f方向上的备选列车集，nf表示出发列车数(亦可理解为末班车编号)，为决策变量，则出发列车集Lf(nf)={l|l∈Df,l≤nf}是经条件l≤nf过滤而生成的关于Df的内P-集合[11]，根据区间集合Qf和列车集合Lf(nf)，将列车l与其运行区间q称为一个(l,q)，记Bf为f方向所有(l,q)组成的集合，表示列车l∈Lf(nf)在首发站的发车时间，为决策变量。

城轨客流具有明显的时变性，但在较短间隔内近似服从均匀分布。据此，将运营时段[T1,T2] 划分为K个客流时段，对于∀s∈Sf，假定时段k内的乘客以客流占比均匀进站，进站人数为τs,f(k)。乘客进站后在站台上等待列车，期间产生候车时间。上车人数μl,s,f取决于候车乘客和列车剩余载客能力Δcl,s,f，对于未上车的乘客则需要等待下趟列车。根据上车人数便可确定列车的载客人数，计算效益损失。据此，城轨列车运行计划优化问题描述为：运营时段[T1,T2]内，在满足行车时间、设备能力及列车接续等约束条件下，依据候车时间和效益损失，优化决策变量nf、和δl′,l,f，以期得到兼顾乘客和城轨企业双方利益的城轨列车运行计划。

2 候车时间及效益损失

2.1 候车时间

在考虑乘客滞留的情况下，候车时间可通过最大潜在候车时间与节省候车时间的差值确定。对于t∈[T1,T2] 时进站的乘客而言，其最大潜在候车时间指该乘客自进站至运营时段结束的时间段，即T2-t。节省候车时间指乘客自乘车出站至运营时段结束的时间段，即。为进一步描述，给出s站累计进站客流和累计出发客流曲线如图1所示。

图1 s ∈Sf 站累计进站客流和累计出发客流曲线Fig.1 Cumulative inbound and cumulative outbound passenger flow at station s ∈Sf

显然，s∈Sf站所有乘客的最大潜在候车时间等于图1中累计进站客流曲线与时间轴([T1,T2] 段)所围成的面积(若干梯形面积之和)。据此，运营时段[T1,T2]内，线路上所有乘客的最大潜在候车时间为

式中：τs,f(k)为客流时段k内进入s∈Sf站的乘客人数；为T1时刻已在s站候车的乘客人数；t1(k)和t2(k)分别为时段k的起止时间。

同理，s∈Sf站所有乘客的节省候车时间等于图1 中累计出发客流曲线与时间轴所围成的面积(若干矩形面积之和)。据此，线路上所有乘客的节省候车时间为

显然，s∈Sf站所有乘客的实际候车时间等于图1中的阴影面积，即最大潜在候车时间与节省候车时间的差值。因此，线路上所有乘客的实际候车时间Z1为

2.2 效益损失

根据定义，列车载客过多或过少均导致企业效益损失，且损失程度与导致损失的乘客人数及其持续时间有关。为此，引入1 组参考点c1和c2，且c1＞c2。其中，c1表示列车载客过多时因考虑安全隐患及服务质量等因素而使运营效益为0 的载客人数，c2表示列车载客过少时因考虑客票收入及资源投入等因素而使运营效益为0 的载客人数。据此，因列车载客过多而导致效益受损的乘客人数为

式中：cl,q,f为(l,q)∈Bf上的乘客人数。

显然，对于任意指定的(l,q)及乘客人数cl,q,f，其对应的和均为非负值，且不可能同时取正。因此，可通过取两者的极值确定导致效益损失的乘客人数Δcl,q,f为

考虑到损失状态在列车各区间运行过程中的持续效应，结合效益损失的定义，给出效益损失的计算式为

式中：tq,f为列车在区间q上的运行时间。

3 城轨列车运行计划优化模型

3.1 模型构建

3.1.1 目标函数

以候车时间和效益损失为优化目标能够有效确保乘客时效性和企业运营效益，且两者量纲的统一也有利于方案决策和分析。值得注意的是，城市轨道交通客流的时空分布差异，必将导致部分关键(l,q)上出现乘客超拥挤或极少的极端情况，使列车运营过程中的效益存在较大损失且无法避免[13]。为此，特别引入调控因子Γf以控制决策关键(l,q)，通过赋以不同的权重体现关键(l,q)和非关键(l,q)上效益损失的差异性。据此，构建基于候车时间和效益损失的城轨列车运行计划优化目标为

式中：Uf为由Γf个关键(l,q)构成的集合；BfUf为非关键(l,q)所构成的集合；ϖ0为候车时间权重；ϖ1和ϖ2分别为关键(l,q)和非关键(l,q)上的效益损失权重，且ϖ1＞ϖ2。

3.1.2 约束条件

(1)列车开行数量约束根据备选列车集合Df，列车开行数nf的约束为

(2)时刻表相关约束

①时间递归约束

列车在各站的到达时间和发车时间为

②首末班车时间约束

为避免乘客过早等待早班列车和错过末班列车，首班车和末班车的发车时间一般根据乘客出行习惯及线路性质等因素预先确定。根据运营时段[T1,T2]，首班车和末班车时间约束为

式中：Tf为f方向列车的单程运行时间，计算公式为

③列车间隔时间约束

为确保行车安全，相邻列车间应满足最小的发车间隔时间Imin。此外，为避免乘客长时间等待列车，相邻列车的发车间隔不应大于间隔时间Imax。

(3)列车接续相关约束

列车接续约束是确保运行计划顺利实施的关键，包括列车数量约束和接续时间约束两部分。为刻画折返线能力受限下的列车接续及进出场环节，根据列车l在首发站的发车时间及其在终到站的到达时间，引入与之相对应的状态变量和为

①列车数量约束

两端配有车场的城轨线路上，f方向的始发列车由其配属车场所提供的列车或由1-f方向的终到列车担任，即

式中：Mf为f方向首发站车场可提供的列车数。

②接续时间约束

当1-f方向终到列车l′担任f方向列车l的运输任务时，列车l′因折返而产生折返时间当折返线能力饱和时，列车l′在终点站清客后，需前往车场临时待避。据此，接续时间约束为

式中：M为充分大的正数；Δt1-f为1-f方向终到列车的进出场作业时间；δl′,l,f为列车接续决策变量，若列车l与列车l′存在接续，δl′,l,f=1，否则，δl′,l,f=0；φl′,1-f为辅助变量，表示列车l′到达终点站后是否因折返线能力限制而前往配属车场，判断条件为

式中：N1-f为1-f方向终点站折返线的最大存车能力。若式(22)成立，取φl′,1-f=1；否则，φl′,1-f=0。

综合上述目标函数和约束条件，即构建城轨列车运行计划优化模型M.1，模型中决策变量为：列车开行数nf、列车始发时间及列车接续关系δl′,l,f。

3.2 模型性质及等价变换

模型M.1 中，关于效益损失的目标函数Z2,f是基于关键(l,q)集合Uf、非关键(l,q)集合及其调控因子Γf而构建，但如何合理划分关键(l,q)和非关键(l,q)，模型中未明确说明。此外，模型中的优化目标函数只是一种便于理解的形式化表述[14]，不利于模型的直观求解。综上考虑，对模型M.1进行等价变换。

定理2 线性规划模型式(23)～式(25)的对偶问题为

式中：pf∈R和zl,q,f为式(24)和式(25)所对应的对偶变量。

证明 式(23)所示的目标函数

而该模型的对偶问题为式(26)～式(28)所示的线性规划模型，证毕。

根据定理1 和定理2，模型M.1 可等价变换为模型M.2，即

s.t.式(10)～式(14)、式(16)～式(17)、式(20)～式(21)及式(27)～式(28)。

易证得，模型M.2等价于模型M.3，即

s.t.式(10)～式(14)、式(16)～式(17)、式(20)～式(21)及式(27)～式(28)。

模型M.3 中的决策变量为：列车开行数nf、始发时间、接续关系δl′,l,f及对偶变量pf和zl,q,f。该模型为非线性混合整数规划模型，目标函数Z1部分为二次项，目标函数Z2,f则是对模型M.1中Z2,f部分的等价变换。与模型M.1 相比，模型M.3 增加了一组对偶变量和一个约束条件(非负约束除外)，但解决了关键(l,q)和非关键(l,q)的划分问题，同时，其目标函数的标准化表述也方便了模型的直观求解。

4 基于GA-Gurobi的混合求解策略

模型M.3 是在备选列车集合Df的基础上，根据关于决策变量nf的出发列车集合Lf(nf)而构建，其非线性混合整数特性，使计算耗时与集合Df中的备选列车数呈指数增长。特别地，从模型变换过程可以看出，对偶变量pf和zl,q,f是依据预先得到的关于的可行解而确定，故而难以用现有的求解器直接求解模型M.3。为此，本文设计基于GA-Gurobi的混合求解策略，其核心思想为：根据特定的染色体编码，将有效个体解码为关于的可行解，经客流加载，确定候车时间Z1和效益损失wl,q,f，然后，根据可行解，利用Gurobi求解式(26)～式(28)所示的线性规划模型，得到模型M.3 中的对偶变量pf和zl,q,f，进而确定模型M.3的目标函数值，并据此设计适应度函数评价有效染色体的质量。最后，经有限次遗传操作便可寻求满足最优准则的相对较优解。

4.1 个体编码及适应度函数

本文采用二进制的双倍染色体编码方式，即每个个体G=(X,Y)包含1 对染色体X=(x1,x2,x3,…,xσ)和Y=(y1,y2,y3,…,yσ)对应运行方向f。对于染色体A∈{X,Y}，其基因ai∈{xi,yi} 采用0-1 编码，若基因i对应的时刻有该方向列车始发，ai=1；否则，ai=0。

定义1 对于染色体A∈{X,Y}，将基因值标记为“1”及其后继连续标记为“0”的若干个基因称为染色体A的一个基因片段，并将其基因个数称为基因片段的长度。

根据定义1，将染色体上的基因片段依次编号，并与列车编号相对应。据此，二进制双倍染色体编码如图2 所示。图2 中，A.l表示染色体A∈{X,Y}上编号为l的基因片段。根据双倍染色体G，便可得到列车开行数nf及列车的始发时间，进而根据时间递归公式和客流分配策略确定上车人数、候车时间和效益损失。在此基础上，利用Gurobi求解式(26)～式(28)所示的线性规划模型，便可得到M.3中的对偶变量pf和zl,q,f。

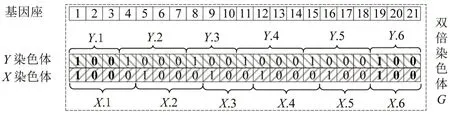
图2 二进制双倍染色体Fig.2 Binary diploid chromosome

因首末班车的发车时间是固定的，个体编码时，将其对应基因片段的起始基因位置预设为恒定(如图2 中的X.1Y.1 和X.6Y.6)。此外，因个体信息不能体现列车最小间隔及其接续关系，为避免客流分配及Gurobi在非有效个体上的计算，设计个体G的适应度函数F(G)为

式中：M为充分大的数；Θ(l)为检查列车间隔时间约束及列车接续约束的函数，若个体对应解中列车l的发车时间均满足式(16)～式(17)及式(20)～式(21)，Θ(l)=1，否则，Θ(l)=0。

约束检查时，列车接续关系可通过以下原则确定：当1-f方向无终到列车或终到列车已被分配殆尽时，f方向列车由该方向配属车场中的空余列车担任；否则，在优先使用折返线上未被分配列车的前提下，按“先到先发”原则确定出发列车的接续列车，以减少列车空走距离和车场备用列车数。

4.2 进化操作及策略流程图

定义2 个体G和G′中的对应染色体A和A′，若i为基因片段A.l1和A′.的起始基因座，j′(j′＞i)为基因片段A.l2和A′.的末端基因座，则以i为始端和j=min{j′} 为末端的基因序列称之为对应染色体A和A′ 上的一组最小可交基因片段，记为A⊗A′.[i,j]。

根据适应度函数F(G)，采用精英个体与轮盘赌相结合的选择策略确保算法的收敛性和全局最优。交叉操作时，根据定义2，依概率选取父代染色体上对应的若干组最小可交基因片段A⊗A′.[i,j]，通过多点交叉策略尽量确保子代的有效性。变异操作时，随机选取长度大于间隔时间I的基因片段进行0-1随机替换，并利用Θ(l)函数实时检测变异结果的有效性。求解策略的最优准则为：(1)最大迭代次数E1；(2)精英个体在E2次迭代中未被更新。基于GA-Gurobi的混合求解流程如图3所示。

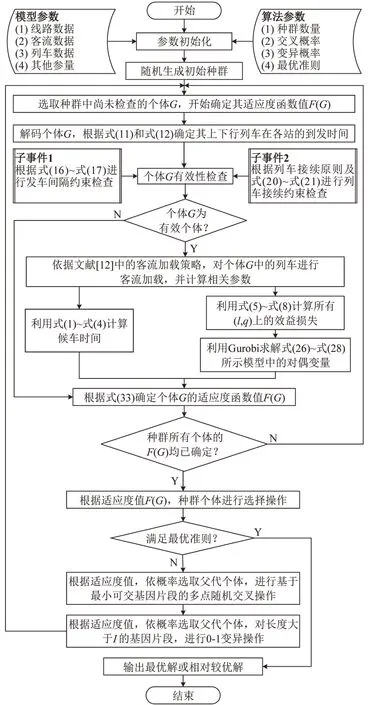
图3 基于GA-Gurobi的混合求解流程Fig.3 Hybrid solution flow based on GA-Gurobi

5 算例验证

5.1 算例描述及参数设置

以某城市轨道交通线路为例。线路设29座车站，单程运行时间76 min。车站编号、停站时间及区间运行时间如图4所示。图4中，圆圈表示车站，圆圈上方加粗数字表示车站编号，圆内数值表示停站时间(min)，两圆连接线上的数值表示区间运行时间(min)。车站1 和车站29 为配有车场的首发站，其余为中间站。车场提供列车Mf=0=15 列，Mf=1=17 列，进出场时间Δtf=4 min。折返线最大存车数Nf=2列，折返时间=3 min。列车发车间隔Imin=3 min，Imax=15 min，且c1=600 人·列-1，c2=1500人·列-1，c3=2000人·列-1。运营时段选取线路某日6:00-12:00。该时段内，上行客流比较均衡，下行客流具有较强时变性，高峰时段为7:20-9:30。根据所选时段，以15 min为步长，将其划分为24个客流时段，进站人数及客流占比受篇幅所限不再详举。求解策略中，种群规模为20，交叉变异概率分别取0.75和0.08，最优准则E1=350，E2=100。模型中调控因子，权重系数ϖ2=0.4ϖ1，ϖ0和ϖ1的取值规则为：根据历代种群有效个体的候车时间和效益损失，利用文献[15]的改进熵权法确定其权重值，并标准化为1∶ϖ1，以便于结果对比和量化分析。初始时，ϖ1=1。

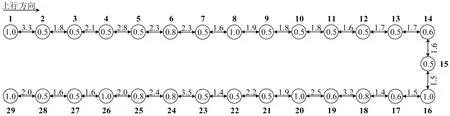
图4 车站编号、停站时间及区间运行时间Fig.4 Station number,stopping time and interval running time

5.2 求解过程及最优结果

以PyCharm为开发环境，通过Python编程并调用Gurobi 模块，算法迭代231 次结束，收敛过程如图5所示。

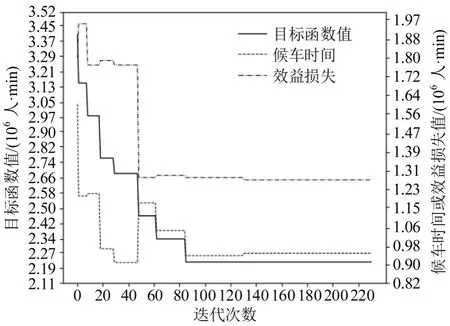
图5 算法收敛过程Fig.5 Algorithm convergence process

图5中，当算法迭代至131次时，发现满足最优准则的较优解，其目标函数值2219415.1人·min，候车时间946834.7人·min，效益损失1272580.4人·min。另从收敛过程可以看出，候车时间和效益损失并非严格相关，例如，算法迭代至30 次时，虽寻得候车时间较小的可行解，但因效益损失较大使目标函数值较差。因此，寻求合理的发车间隔以同时减少候车时间和效益损失显得尤为重要。满足最优准则的列车运行计划如图6所示。

图6 满足最优准则的列车运行计划Fig.6 Train operation plan that meets optimal criterion

如图6 所示，上行方向开行列车43 列，车场提供14列，小于可供列车数15列；下行方向开行列车44列，车场提供17列，等于可供列车数17列。列车间隔时间方面，上行列车间隔比较均衡，大部分保持在5～7 min，下行非高峰时段的最大间隔约为9 min，高峰时段则为3～5 min，且部分车站出现乘客滞留。列车接续方面，4 列上行列车和7 列下行列车因折返线能力受限而入场待避(如空心箭头线所示)，且下行列车10 入场待避后又出场担任上行列车24的运输任务(如黑虚线框所示)，可见考虑列车进出车场环节具有一定的必要性。此外，优化结果中有3列列车(上行1列，下行2列，如灰色矩形所示)按最小折返时间3 min接续，应重点关注。

5.3 结果对比及参数分析

为分析模型M.3优化策略的合理性，给出优化结果参数值及其对比如表1所示。

表1 优化结果参数值及其对比Table 1 Parameter values of optimization results and their comparison

相较于企业方案，模型M.3 减少候车时间408400.2 人·min，约30.1%；节省列车数7 列，约7.4%；减少效益损失277844.9 人·min，约17.9%。可见，模型M.3 能在节省列车数量的同时，还能减少候车时间和效益损失。为了分析效益损失与满载率之间的内在关系，给出优化结果中效益损失和满载率的分布情况如图7所示。

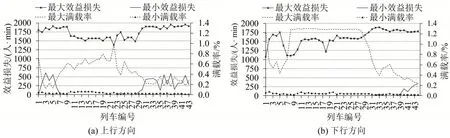
图7 优化结果中效益损失及满载率分布情况Fig.7 Distribution of benefit loss and load factor in optimization results

图7 中，阴影部分表示效益损失为0 时的满载率取值范围。从图7 中可以看出，优化结果中，下行方向列车的最大满载率整体大于上行方向，但两者的最小满载率差别不大且相对较小。另从最大满载率和最小满载率偏离效益损失为0 时的满载率程度看，较小的满载率是产生效益损失的主要因素，且上行方向尤为明显。为分析发车间隔I对目标函数的影响，在不考虑列车接续约束和最大发车间隔约束条件下，给出不同间隔时间对目标值的影响如图8所示。

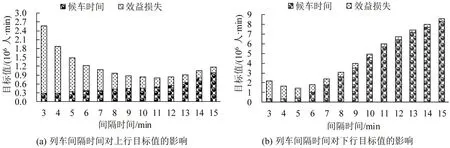
图8 列车间隔时间对目标值的影响Fig.8 Inference on target value caused by train interval time

图8(a)中，当I∈[3,11] 时，上行方向的目标值随I的增大而减小，说明效益损失的减少大于候车时间的增加；当I∈[11,15] 时，目标值随I的增大而增大，说明候车时间的增加大于效益损失的减少。图8(b)中，当I∈[3,5] 时，目标值随I的增大而减小；当I∈[5,15] 时，目标值随I的增大而增大。上述分析说明，算例中的列车若按均衡运行图开行，上行方向较合理的间隔时间为11 min，下行方向为5 min。为分析调控因子对优化结果的影响，以图6 所示的运行计划为例，不同γf取值下的效益损失如图9所示。

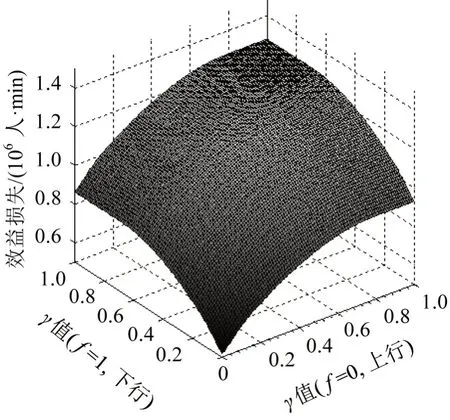
图9 不同γf 取值下的效益损失Fig.9 Benefit loss with different γf

由图9 可知，效益损失随γf值的增大而增大，其主要原因是γf值代表关键(l,q)∈Bf的占比。当γf∈[0.6,1.0] 时，效益损失趋于平缓，说明在其他参数给定时，图6 所示的运行计划中约60%的(l,q)对处于损失状态。

6 结论

本文重点刻画折返线能力受限下的列车折返及进出场环节，以最小化候车时间与效益损失上确界的和为优化目标，研究两端设有车场的城轨列车运行计划优化问题。经研究发现：

(1)考虑候车时间和效益损失能够兼顾乘客和企业的双方利益，但候车时间和效益损失并非严格相关，寻求合理的发车间隔能够同时减少候车时间和效益损失；

(2) 断面客流的不同需求使各运行区间上的效益损失存在差异性，优化结果中，约60%的运行区间处于效益损失状态，说明效益损失具有不可避免性；

(3) 基于车底数量及折返线能力受限的实际情况，城市轨道交通方向客流的需求差异导致终到列车入场待避及再出场环节，该过程在优化结果中有所体现，说明建模时考虑该环节具有其现实必要性。