考虑候选站点和全服务过程的需求响应接驳公交调度

任婧璇，常孝亭，巫威眺*，靳文舟

(1.华南理工大学，土木与交通学院，广州 510640；2.广州市黄埔区住房和城乡建设局，广州 510530)

0 引言

随着经济的持续发展，我国机动化水平逐渐提高，据公安部统计[1]，截至2022 年3 月底，全国机动车保有量达4.02 亿辆。随之产生的交通拥堵等问题日益严峻，公交优先的必要性和重要性尤其凸显。线网优化和多模式公交等策略应用于公交系统以提高公共交通吸引力。然而，常规公交的固定线路和固定班次的特性决定了其不适用于需求较为分散的区域或时段，因此，产生了具有可响应特定需求的公交形式。交通运输部于2020年发布的《交通运输部关于推进交通运输治理体系和治理能力现代化若干问题的意见》[2]中提出完善交通出行保障政策体系，完善交通运输新业态发展制度，建立定制公交等需求响应型出行服务体系。需求响应公交(Demand Responsive Transit,DRT)最早源于为老年人和残疾人等移动能力受限的特定人群服务的电话预约公交(Dial-A-Ride,DAR)，随着科学技术的发展及人们对出行灵活性和舒适度等需求的增长，开始发展面向大众的服务模式。其特点在于可在某种程度上对需求进行响应，亦可称为灵活公交。作为一种介于传统的常规公交和出租车之间的兼具灵活性和集约性的出行方式，DRT可服务个性化的出行需求，并在每次派遣车辆前，根据实际需求及运营目标规划路径和时刻表，实现不同个性化需求间的共乘，较为灵活地调整服务的个性化和集约化的程度，在未来出行中具有较大的潜力。

根据DRT 系统的运营模式和灵活度将其细分为：可变线路公交、可变站点公交、需求响应接驳公交、站点需求响应公交、部分线路可变公交及区域线路公交等形式[3]。近年来，国内发展出具有相似特性的定制公交服务，现有定制公交系统多通过提前的线路征集确定线路的起终点及走向和乘客的可选站点[4]。其中，需求响应接驳公交(Demand Responsive Feeder Transit,DRFT)是用于接驳大型集散点的需求响应公交，为出行的第一公里和最后一公里服务，其中“一公里”主要指整个出行过程的最初或最后一段，而并非特指空间上的1 km。

现有DRT 调度研究多集中在可变线路式公交及需求响应接驳公交的路径规划问题，其中，路径规划的站点多直接以需求点作为乘客上车点，与站点相关的研究多为具有一定需求响应特性的定制公交和可变线路公交的线路规划，进一步转化为不同约束和不同目标下的车辆路径问题(Vehicle Routing Problem,VRP)。例如，QIU等[5]在可变线路公交背景下，将已接受的站点作为临时站点，可供被拒绝的需求作为上下车点选择。需求响应接驳公交需求的上下车站点通常由需求自行指定某一车辆可停靠站点或需求所在实际位置，系统根据路径规划确定遵照需求意愿或在一定范围内进行调整分配。例如，ZHENG 等[6]研究可变线路公交，其中，乘客指定唯一上下车点，但系统在规划路径时可将需求分配到附近的集合点。仅JIANG 等[7]考虑了需求离开接驳系统时可选择多个站点作为服务的终点，在高峰期运力不足的情况下服务尽量多的需求。现实中，需求进入接驳系统时通常有多个步行可达站点可供选择，需求间共同的可达站点可提高共乘的可能性，从而提高运输效率。REN等[8]考虑需求有多个不同等级的备选站点下的需求可取舍的接驳系统。

在需求的时间要求方面，较为典型的为带时间窗的VRP问题，其中，需求点的服务必须在特定的时间段内开始，该时间段即为时间窗。在此基础上进一步发展的考虑同时取送货的PDP问题(Pickupand-Delivery Problem)兼顾了取货点和送货点的时间窗。在乘客运输中，则对应了DAR 问题中乘客上车点和下车点可开始服务的时间段，其上车点的时间窗表示最早出发时间至最晚出发时间之间的时间段，下车点的时间窗表示最早到达时间至最晚到达时间之间的时间段。除服务开始时间的时间窗外，另一个常被考虑的时间需求为行程时间的长度。在DRT 研究中，需求的时间要求亦是重要的路径规划约束，例如，JIANG等[7]考虑需求的时间窗和以行程时间为基础的服务质量优化高峰期接驳公交路径；REN 等[8]考虑需求指定的上车时间窗；安久煜等[9]在去程回程双向的高铁接驳公交路径优化问题中考虑回程时间应晚于去程时间；陈汐等[10]在通勤定制公交中考虑上车时间窗为期望出发时间附近浮动一定的缓冲时间；LU 等[11]将需求响应接驳公交的乘客分为前往换乘点的和从换乘点出发的两种类型，并对两种类型需求的期望时间分别进行一定的偏移，得到时间窗；LI 等[12]考虑需求响应接驳公交的背景下乘客指定1个上车时间窗，且其位置信息已知，系统在一定的时间窗偏离范围内为需求规划上车站点和时间窗。总体而言，现有DRT研究多考虑需求出发或到达的单点(上车点或下车点)时间窗，及乘客行程时间约束。时间窗的上下界由需求指定，或在需求指定的时间点附近允许进行一定的偏移。

综上，需求响应接驳公交的调度研究缺乏考虑提高共乘可能性及系统效率的乘客进入系统的多项选择，以及缺少从整体角度对服务过程的时间范围进行约束的考虑。以服务“第一公里”接驳火车站的需求响应接驳公交为例，乘客须从家乘坐接驳公交到达火车站，再乘坐火车到达最终目的地。接驳公交服务该出行的前半段，即从家到火车站。因乘坐的火车有固定的发车时间，因此，接驳服务的最晚到达时间受该发车时间限制。火车发车时间除对接驳服务的到达时间有约束外，对接驳服务的起点也产生影响。尤其是火车发车时间很早或很晚，乘客无其他交通方式可选，则对接驳公交寄予更多希望，可能对上车位置的要求进行一定的妥协，即添加候选站点。另一方面，从出行目的角度考虑，出行的目的在于到达目的地，而非移动过程本身。在出发之前，乘客处于舒适的居住地，可进行生产力工作或休闲娱乐；一旦出发，乘客则处于活动受限且舒适度下降的移动过程。因此，乘客希望尽量推迟出发时间，而为保证不晚于接驳终点的最晚到达时间，乘客对出发时间的推迟应有界限，即设置一个最早出发时间。最早出发时间和最晚到达时间之间的间隔由乘客依据对接驳系统的速度和舒适性等因素的预期进行设定。由此，乘客对接驳服务全过程的开始和结束时间设置上下界，即全服务时间窗。区别于常见的出发或到达的单点时间窗将运输服务视为割裂的上车、在车及下车这3 段，全服务时间窗从整体上把握为乘客提供的运输服务，综合了乘客对出发、到达及行程时间的要求，将服务水平的决定权部分让渡给乘客。这一设置符合接驳公交系统中接驳终点的高时效性以及乘客对从居住地到出行过程的抵触。而现有文献中却鲜有研究这一符合实际的时间窗要求。

有鉴于此，本文提出考虑需求的多个互斥候选站点和包括需求最早出发时间和最晚到达时间的全服务过程时间窗的服务出行第一公里的需求响应接驳公交调度问题，实现对车队规模配置和车辆路径的联合优化；并在基于实际路网的案例上进行实验，分析候选站点和全服务时间窗对系统性能和乘客行程时间的影响。

1 模型建立

1.1 问题描述

本文的需求响应接驳公交系统以大型接驳站为需求服务终点，车辆从车场出发，访问并服务站点后将需求送至目的接驳站。需求在预约系统内提交出行预约，预约信息包含候选上车站点集合，目的接驳站及全服务时间窗。不同于普通意义上的出发或到达时间窗，全服务时间窗指在上车站点的最早出发时间及到达出行终点的最晚到达时间。运营方在收到预约需求后，首先，需求进行站点分配及车辆路径规划，然后，经预约系统向乘客反馈具体的服务信息。由此可见，本文研究的需求响应公交系统调度所涉及的子问题较多，包含车队规模的确定，需求的互斥候选站点的选择及车辆路径问题。预约系统示例如图1所示。

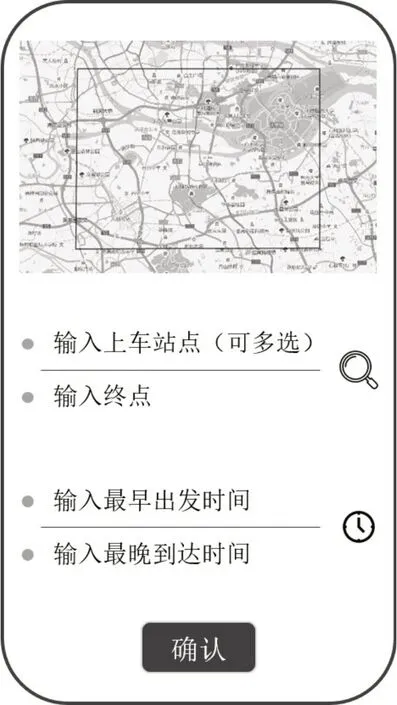
图1 预约系统示例Fig.1 Illustration of a reservation system

需求响应接驳公交系统示例如表1 和图2 所示。假设需求的全服务时间窗在以下路径构建过程中均不会被违反。若每个需求只指定一个上车站点，需求1，2，3分别选择站点1，3，5，此时车辆须分别访问3个站点才能服务所有乘客，即车辆路径1为车场-站点1-站点3-站点5-终点，路径距离为12。若每位乘客均可选择多个候选站点，需求a选择步行可达范围内的站点1和站点2，需求2选择站点3和站点4，需求3选择站点4和站点5。此时，车辆仅通过访问1 个站点(站点4)即可服务乘客2 和乘客3。另外，在站点2服务乘客1相较于站点1也可以减少车辆的行驶距离。由此，需求的站点选择结果为需求1为站点2，需求2为站点4，需求3为站点4；车辆路径2为车场-站点2-站点4-终点，路径距离为8。两种情况下的路径如图2所示。

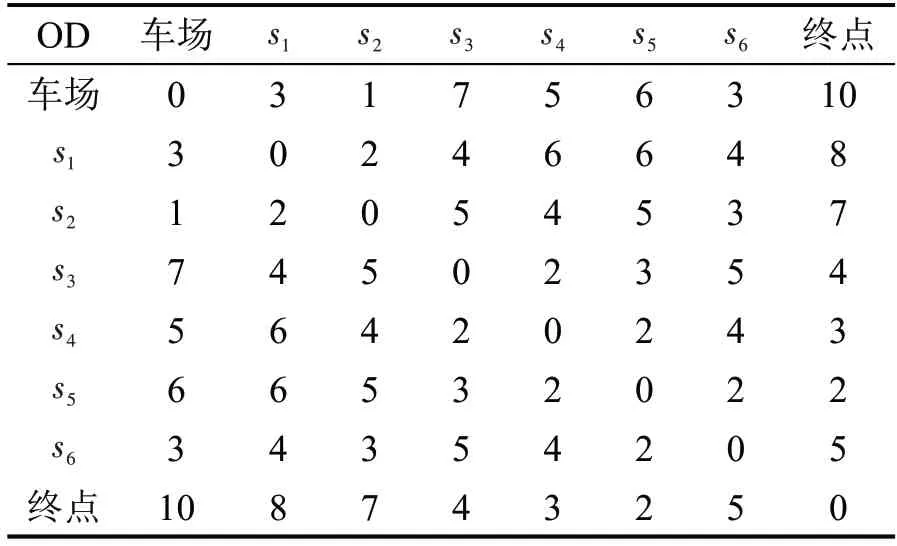
表1 示例系统的距离矩阵Table 1 Distance matrix of sample DRFT system

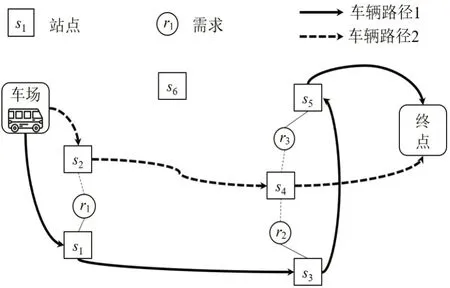
图2 需求响应接驳公交系统示例Fig.2 Illustration of a DRFT system

为降低问题维度，本文基于候选站点构建虚拟站点到实际需求集合和实际站点集合的映射，并构建考虑节点关系与空间距离的虚拟节点间的阻抗矩阵，将本文的复杂调度问题转化为带有全服务时间窗和容量约束的车队规模确定和车辆路径问题(Fleet Size Determination and Vehicle Routing Problem with Capacity and Full-Service Time Windows,FSVRP-C-FSTW)。

1.2 问题预处理

1.2.1 需求集合与站点集合

为描述基于需求候选站点需求响应公交的调度问题，将实际潜在站点集合记为S，实际需求集合记为R。需求集合中的每个需求r的信息包括由最早出发时间和最晚到达时间构成的全服务时间窗[er,lr]和从潜在站点集合中选择的若干站点构成的候选站点集合Ur(Ur⊆S)。以图2 所示的接驳公交系统为例，需求信息如表2所示，其中，所有需求的全服务时间窗均假设为[0,15]。需求的互斥候选站点的选择即从每个需求指定的多个候选站点中选择，该设定使各站点的需求量构成具有一定的随机性，因此，增大了车辆路径规划的难度。为降低问题维度，从实际候选站点的角度出发，将被多个需求选择的同一实际站点复制若干次，得到对应同一实际站点的多个包含不同需求信息的虚拟站点。经以上步骤构建的虚拟站点集合记为P。从而，实际需求集合R、实际潜在站点集合S及虚拟站点集合P之间构成以下映射。

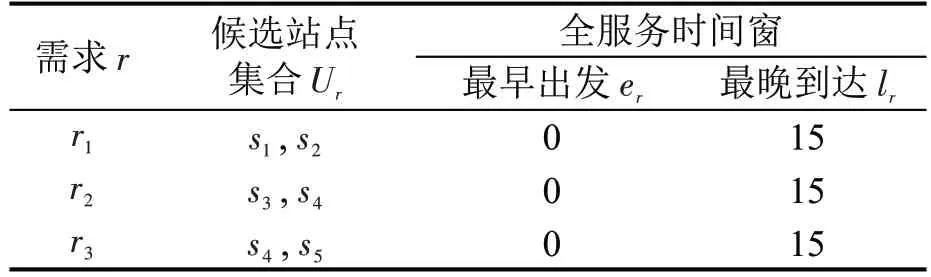
表2 需求信息示例Table 2 Illustration of demand information

f1:P→R为虚拟站点集合到实际需求集合的满射但非单射；f2:P→S为虚拟站点集合到实际潜在站点集合的非满射非单射(存在未被任何实际需求选择的站点)。以图2 的接驳公交系统和表2的需求信息为例，该系统对应的实际需求集合、实际潜在站点集合及构建的虚拟站点集合如表3 所示，集合间的映射如图3所示。

表3 需求与站点集合示例Table 3 Illustration of request set and stop set

图3 集合映射示例Fig.3 Illustration of mappings

1.2.2 阻抗矩阵的构建

为定义虚拟站点之间及其与车辆出发车场和接驳终点间的阻抗，本文的需求响应公交问题可定义在完全有向图G=(V,A) 上，其中，节点集合V=O∪P∪D，O={0}为代表车场的单元素集合；P={1,2,…,|P|}为生成的虚拟站点集合，记虚拟站点数量为n，即 |P|=n；D={n+1} 为表示接驳终点的单元素集合。A为集合V中节点间弧的集合。

基于虚拟站点集合P与实际需求集合R和实际站点集合S间的映射关系，本文将节点间的阻抗定义为节点间关系与空间距离的结合。实际站点集合S中两两之间及车场和接驳终点与实际站点间的行驶时间可通过直线距离和路径距离等方式测算，对集合P中虚拟站点两两之间的距离及行驶时间须由虚拟站点到实际站点间的映射关系确定，即及，使转化后的问题与原问题的约束、目标及解相同。

考虑需求指定多个候选站点的特点，本文定义并量化节点间的需求对应与空间关系，引入矩阵Θ和矩阵Φ分别表示节点间的需求对应关系和位置关系，其中，元素θij和φij分别表示节点i和j(i,j∈V)是否对应同一实际需求或同一实际站点，其值由表4 确定。若节点i和j均为虚拟站点，即i,j∈P，则θij和φij为逻辑判断得到的布尔值的整数型(0 或1)。为系统描述所有候选站点的需求对应关系，引入平均候选站点数量(记为uˉ)和与之相关的需求同质度(记为HP)指标定量化描述所有需求。假设指定u(u∈ℕ+)个候选站点的需求量为mu，则指定不同候选站点的需求量之和为需求集合R的基数，即。由候选站点的构建过程可计算所有的候选站点数量，即集合P的基数为，所有候选站点间的需求对应参数之和为。由此，所有需求的平均候选站点数量，所有候选站点的需求同质度

表4 θij,φij 的确定Table 4 Determination of values of θij,φij

1.3 模型假设

为描述考虑候选站点和全服务时间窗的需求响应公交调度问题，做如下假设：

(1)需求所指定的出发时间窗下界和到达时间窗上界之间的时间间隔须大于其候选起点至讫点间的直接行驶时间的最大值；

(2)假设需求集合R每个需求的需求量均为1，若存在某个需求的需求量大于1，则将其复制裂变成多个需求量为1的预约信息相同的需求；

(3)服务过程中不存在换乘；

(4)乘客按照规划的时间到达既定站点，不考虑乘客的晚到和不到情况；

(5)假设可使用车辆足以服务所有需求。每辆车完成1个车次任务，即将所有需求送至接驳终点站后即结束行程，不考虑单车执行多车次任务或返回车场。

1.4 模型参数

主要模型参数解释如下：

G=(V,A)——节点集合V和节点间弧的集合A构成的有向图，其中，V=O∪P∪D，即节点集合包含车场集合O={0}，虚拟站点集合P={1,2,…,n}，终点集合D={n+1} ；

R——实际需求集合，R={1,2,…,|R|}；

K——车辆集合，K={1,2,…,|K|}；

Q——车辆的额定载客量(人·车-1)；

[ei,li]——节点i∈V的全服务时间窗，若i∈P，表示虚拟站点的全服务时间窗，即在上车站点上车的最早出发时间和到达接驳站的最晚到达时间，虚拟站点的全服务时间窗应与其对应的实际需求的全服务时间窗相同，即，若i∈O∪D，表示车场或接驳终点的全服务时间窗，两者均设置为整个规划时段；

c1——车辆k的启动成本(元·车次-1)；

c2——车辆单位距离运行成本(元·km-1)；

s——平均每位乘客在站服务时间(s·人-1)；

tij和dij——节点i与节点j之间的行驶时间(s)和路径距离(km)，取决于节点间的需求及空间关系，由构建的阻抗矩阵确定；

Tik——辅助变量，表示车辆k在节点i开始服务的时间；

Lik——辅助变量，表示车辆k离开节点i时的载客量；

Xijk——决策变量，表示车辆k是否从节点i直接行驶到节点j的0-1 变量，若是，值为1，否则为0。

1.5 FSVRP-C-FSTW模型

基于以上映射和阻抗矩阵的构建，本文将考虑候选站点和全服务时间窗的需求响应接驳公交调度问题转化为带有全服务时间窗和容量约束的车队规模确定和车辆路径问题(FSVRP-C-FSTW)进行建模求解。

式(1)为目标函数，表示该优化问题以最小化总成本为目标，总成本包括固定成本和可变成本，其中，固定成本为用于服务的车队规模与单位车辆启动成本之积，可变成本即单位距离成本与总路径距离的乘积。式(2)～式(4)保证所有实际需求均在其指定的候选站点被服务，其中，式(2)表示1 个虚拟站点最多被1 辆车服务1 次；式(3)保证仅指定1 个候选站点的需求一定在其指定的站点被服务；式(4)保证指定了多个候选站点的实际需求仅在其中一个站点被服务。式(5)～式(7)保证车辆从车场出发，访问服务若干站点后到达接驳终点，其中，式(5)保证车辆从车场出发，若车辆从车场出发后访问站点服务需求，则车辆启用，否则车辆不启用；式(6)保证虚拟站点的流平衡；式(7)表示所有从车场出发的车辆最后均在接驳终点结束服务。式(8)～式(10)为载客量约束，式(8)保证车辆空车从车场出发；式(9)确保车辆离开任意点时的载客量不超过其容量；式(10)确保车辆离开任意点时的载客量不低于该点的需求量和离开前一节点时的载客量之和。式(10)和式(11)保证车辆路径中不含有子回路。式(12)和式(13)为全服务时间窗约束，式(12)保证车辆到达接驳终点的时间不晚于其服务的所有需求的最晚到达时间；式(13)保证车辆在任意虚拟站点的开始服务时间不早于该点需求的最早出发时间。式(14)为决策变量的取值约束。

2 模型求解

2.1 精确解

该模型为混合整数非线性规划，其非线性特点由非线性约束式(10)～式(12)决定。为简化模型求解，将式(10)进行线性化处理，即

将式(11)进行线性化处理，即

式中：Mij=max{li-ti,n+1+s(1-φij)+tij-ej,0} 。

将式(12)进行线性化处理，即

式中：M为足够大的正数。

经过对模型中非线性约束进行线性化处理，模型转化为混合整数线性规划模型。本文调用Gurobi 求解器求解模型，其中，为避免因交换车辆下标k而导致的相同解，本文引入车辆编号对称性消除约束，即要求较小下标的需求由较小下标的车辆提供运输服务[13]，其中，需求的服务需在多个候选站点中进行选择。为消除同一实际站点的多个需求服务时的次序不同带来的相同解，引入同站需求序列唯一性约束，即车辆服务某一实际站点时，优先选择较小标号的需求。以图3 和表3 中虚拟站点和需求间的对应关系为例，假设车辆额定载客量为2，对应相同车辆路径的多个解如表5所示。

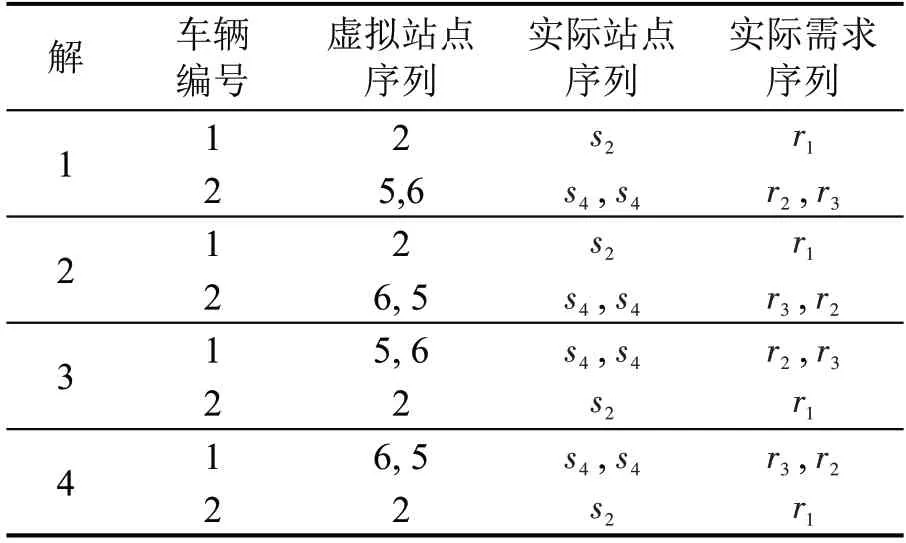
表5 对应相同车辆路径的多个解Table 5 Multiple solutions representing same vehicle routes

其中，4个解均对应相同的路径，即一辆车在实际站点s2服务实际需求r1，另一辆车在实际站点s4服务实际需求r2和r3。通过引入约束可将解2～解4消除，仅保留解1，即

考虑单个需求与多个候选站点之间的对应关系，式(18)保证标号为1 的实际需求对应的所有虚拟需求中有且仅有一个被标号为1 的车辆服务。式(19)保证任意虚拟需求及与其对应同一实际需求的其他虚拟需求被服务的车辆的编号应不大于服务编号小于该实际需求对应的任意虚拟需求的车辆的编号。式(20)保证不同需求在同一实际站点被服务时，标号较小的实际需求对应的站点优先被选择。

经过以上步骤求解得到的为在虚拟节点网络上的车辆路径，通过虚拟站点到实际需求与实际站点的映射关系可得到在实际路网上的需求的站点分配结果与车辆路径。

2.2 自适应邻域模拟退火算法

本文研究的问题可视为带有全服务时间窗和容量约束的车队规模确定和车辆路径问题(FSVRP-C-FSTW)，即带有复杂约束的车辆路径问题，此类问题为NP难问题，在问题规模稍大时即无法实现精确求解，因此，本文设计了一种启发式算法用于求解，该算法针对问题特征设计4种邻域结构，并参考文献[14]在模拟退火算法框架下引入自适应邻域机制。算法主要框架为在内层循环中不断选择邻域结构并生成新解更新当前解；在外层循环中更新温度和邻域选择参数，并更新当前最优解。

2.2.1 解的表示

算法初始化时，将解初始化为虚拟站点的随机序列，序列长度等于实际需求量，每个虚拟站点分别对应不同的实际需求，保证所有需求均被服务。解对应的实际路径则通过首先激活1辆车，根据虚拟站点的序列依次插入当前车辆路径，当后续节点加入违反全服务时间窗和载客量约束时，新增车辆并置为当前车辆，然后，继续依次插入当前车辆路径，以此循环，直至解的所有节点均已被插入某车辆路径。由此可知，算法执行过程中产生的解均满足载客量和全服务时间窗约束，解的目标函数值则通过其对应的实际路径参考目标函数式(1)计算得到。以图3 和表3 中的虚拟站点和需求间的对应关系为例，假设车辆的额定载客量为2，不考虑时间窗约束，表示为3-5-1的解对应的实际路径为车辆1在站点s3和s4分别服务r2和r3，车辆2在站点s1服务r1。

2.2.2 邻域结构

算法内层循环中涉及的邻域结构包括：交换、插入、逆转和需求重置这4 种邻域。以图3 和表3的需求为例，为更清楚地展示不同邻域结构的操作过程，在图3的需求基础上增加指定站点s2和s5的需求r4，分别对应虚拟站点集合P中的新增元素7和元素8。不同邻域结构作用于相同解得到的结果如图4所示，左侧为原解，其中，灰色格子代表邻域操作选择的位置；右侧表示不同邻域作用后的新解，其中，灰色格子代表新解相对于原解的改动。前3 种邻域均需要随机选择序列上的2 个位置，交换邻域将2个位置上的虚拟站点进行交换，插入邻域通过将选中的较前位置的虚拟站点插入到较后位置的虚拟站点之后，逆转邻域则将2个位置间的虚拟站点序列进行翻转。以上3 种邻域结构均不改变需求的站点分配情况。需求重置邻域通过选择序列上的1个位置，将该位置的需求重置到其他候选站点，即实现了需求的站点重分配。

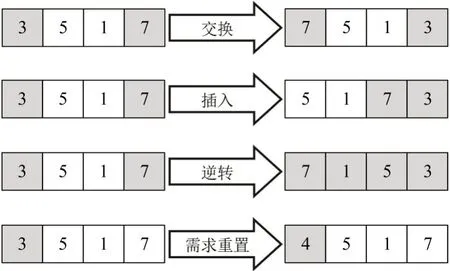
图4 邻域结构示例Fig.4 Illustration of neighborhood structure

图4 中的虚拟站点3 经过需求重置，更换为虚拟站点4。其需求重置过程须首先参考图3中节点集合的映射，得知虚拟站点3 对应实际需求为r2，然后，将该点重置为该需求r2对应的其他虚拟站点，即为虚拟站点4。

内层循环中邻域选择通过轮盘赌实现，每个邻域的选择概率为该邻域结构下已产生解的平均值除以所有邻域结构下产生解的平均值，因此，每次外循环迭代中需更新的邻域选择参数即包括每个邻域已产生解的目标函数的平均值，及所有邻域结构已生成解的目标函数的平均值。

2.2.3 算法流程

该算法的具体流程如下：

Step 1 初始化。生成初始解，并置为当前解x和当前最优解x*。当前温度T初始化为初始温度T0。邻域选择概率初始化为相同的概率。

Step 2 若当前温度T＞最低温度Tf，执行内层循环，即Step 3；否则，执行Step 5。

Step 3 内层循环。

Step 3.1 判断是否满足内层迭代终止条件，若是，执行Step 4；否则，执行Step 3.2。

Step 3.2 轮盘赌选择邻域结构，并在相应邻域内产生新解x。

Step 3.3 若新解优于当前解，则更新当前解；否则，以exp(-ΔT)的概率接受新解为当前解，其中，Δ=f′-f，表示新解目标函数值f′和当前解的目标函数值f间的差。转至Step 3.1。

Step 4 比较并更新当前最优解、温度和邻域选择参数。转至Step 2。

Step 5 输出当前最优解。

3 算例研究

3.1 算例信息

本文以图5 所示的实际路网为案例基础进行实验，以广州大学城内90个公交站点为潜在站点，其中，大学城穗石村总站作为车场，构建面向广州南站考虑候选站点和全服务时间窗的需求响应接驳公交系统。由于本文设想的公交系统尚未落地，因此，实验中的客流需求将依据实际路网生成。站点信息、站点间的行驶距离与行驶时间等信息均通过调用高德地图API 获取。为分析模型性能并分析候选站点和全服务时间窗，本文生成了不同规模的需求场景(实际需求量分别为9，15，30，45)，并分别在Gurobi 求解器中精确求解模型和利用自适应邻域模拟退火的启发式算法求解模型，以验证模型和本文设计算法的有效性。除此之外，对可在求解器内快速求解的小规模算例进行需求参数修改，包括候选站点和时间窗参数，通过求解器求解修改后的算例分析候选站点和全服务时间窗对系统性能的影响。

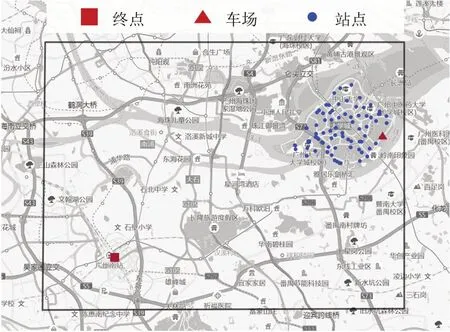
图5 案例的接驳终点和潜在站点Fig.5 Destination and potential stops

为明确不同算例下需求所包含的站点和时间窗参数，设计具有9 个实际订单需求，指定20 个候选站点，即对应20个虚拟需求的案例，需求指定的候选站点及全服务时间窗如表6所示。

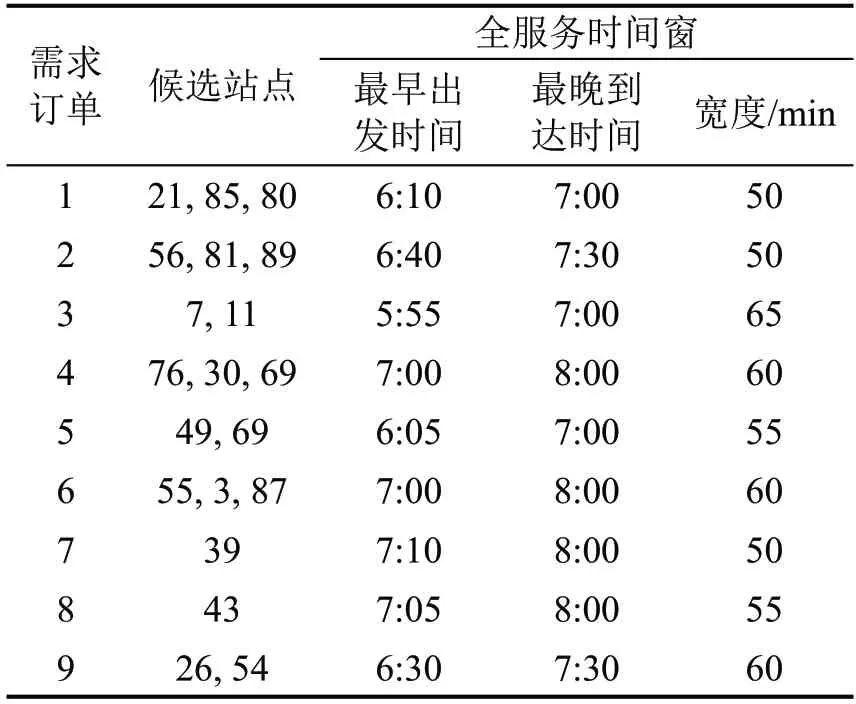
表6 需求订单信息Table 6 Demand information

车场及终点的时间窗设置为5:30-8:00。为分析候选站点对系统性能的影响，以表6 为基础，所有订单的候选站点仅保留第1个站点，其余信息不变，生成订单仅指定唯一上车站点的案例。为分析全服务时间窗对系统性能的影响，以表6 为基础，候选站点信息不变，对时间窗进行修改得到多种时间约束下的案例。

实验所需参数设置如表7所示。其中，模型参数设置如下：车辆额定载客量根据实际需求量不同分别设置为3，5，7，10；车辆启动成本考虑驾驶员薪资和车辆折旧等因素，因车辆均为小车型，且算例中仅考虑单车次服务，因此，参考文献[15]将车辆启动成本设置为20元·车次-1；车辆单位行驶距离成本主要包括燃料成本，设置为1 元·km-1。在站服务时间设置为20 s。算法参数设置如下：初始温度为500，最低温度为1，降温率为0.997，内循环迭代次数为300。算例在配置为Intel(R) Core(TM)i7-7560U CPU@2.40 GHz，16 GB RAM 的计算机上利用MATLAB调用Gurobi求解器及编程实现自适应邻域模拟退火算法求解。

表7 参数设置Table 7 Parameters

3.2 算例分析

3.2.1 模型与算法性能分析

为分析车辆编号对称性消除和同站需求序列唯一性式(18)～式(20)对模型求解的作用，将式(1)～式(9)，式(13)～式(20)构成的模型记为模型1，式(1)～式(9)，式(13)～式(17)构成的模型记为模型2，分别用于求解不同规模的算例，模型求解时间限制在1 h内；同时，本文设计的自适应邻域模拟退火算法也用于求解不同规模的算例，以验证该算法的有效性，结果如表8所示。结果表明，在小规模算例下，两个模型在求解器中均求得最优解，式(18)～式(20)的加入有效加速了模型用于小规模算例的求解。在实际需求量为15和 |P|=37 对应的算例下，不同模型求解得到相同的目标值，但模型1的GAP小于模型2，即模型1 得到的下界高于模型2，表明式(18)～式(20)的加入对于下界的提升有一定作用。而在实际需求量为30 和 |P|=64 对应的算例下，模型1 未能在规定时间内求得可行解，表明式(18)～式(20)的加入增加了模型的求解难度。通过比较求解器和启发式算法求解的结果可得，在小规模算例下，本文设计的自适应邻域模拟退火启发式算法求得的解可达到最优，求解时间介于模型1和模型2 之间；对于稍大规模的算例，启发式算法在显著少于求解器求解时间内，求得的解的目标函数值(即总成本)低于求解器在规定时间内求得的结果。

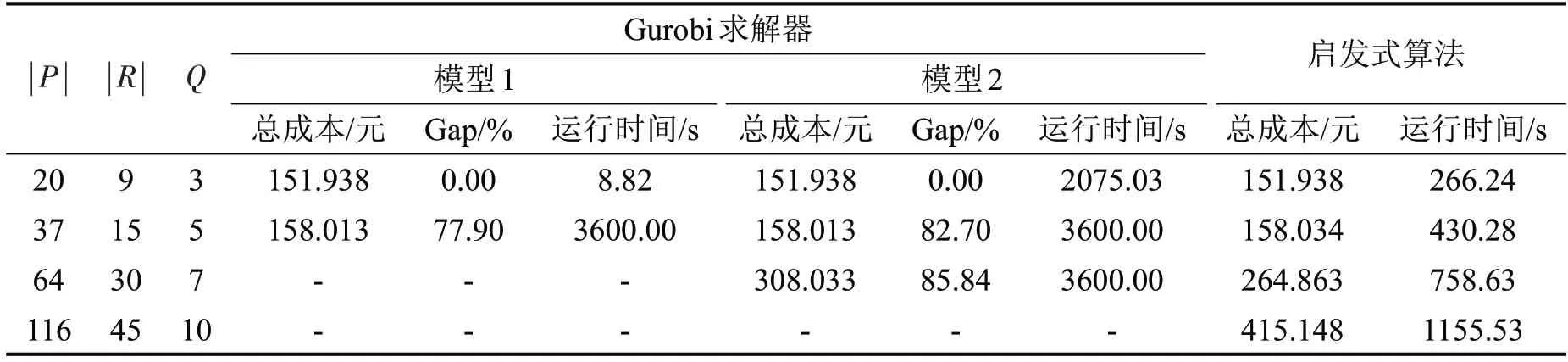
表8 模型与算法对比Table 8 Comparison of models and algorithms

综上所述，车辆编号对称性消除和同站需求序列唯一性约束的引入对于模型在求解器中的精确求解可在一定程度上加速下界的提升，从而加速小规模算例的求解。自适应邻域模拟退火算法在小规模算例中可求得最优解，在稍大规模算例下可在较短时间内求得较优的解。

3.2.2 候选站点的引入对系统的影响

根据算例的需求信息、模型参数及式(1)～式(9)和式(13)～式(20)求解结果分析候选站点的引入对系统的影响，对实际需求量为9 和 |P|=20 的案例中需求指定的候选站点进行删减，得到30个案例，案例信息如表9所示。案例1即为表6对应的基准案例，假设需求指定的多个候选站点均按步行距离升序排列。案例30即为所有需求仅指定唯一上车站点的案例，其他案例均由案例1进行需求的候选站点的修改得到，其中，在减少需求指定站点数量时，优先删减距离较远站点，即表6第2列中靠后的站点。求解所有案例，得到服务需求所需车队规模、车辆总路径长度、乘客平均行程时间和目标值，即总成本。系统总成本和乘客平均行程时间均与Hp，即虚拟站点的需求同质度相关，如图6 所示。就总体趋势而言，虚拟站点的需求同质度较高时，系统总成本较低，同时，乘客平均行程时间较长。原因是，较高的需求同质度值代表车辆访问多个不同的虚拟站点中任意1个均可服务某个需求，从而放松了需求服务对车辆路径的限制，成本得以向目标方向优化，得到较小的总成本；总成本的降低主要源于需求共乘可能性增加带来的所需车队规模的减少，导致乘客行程时间的增加。其中，需求指定多个候选站点的不同案例结果中，相同的总路径长度对应不同的乘客平均时间的原因在于路径服务的站点序列和需求序列的不同。

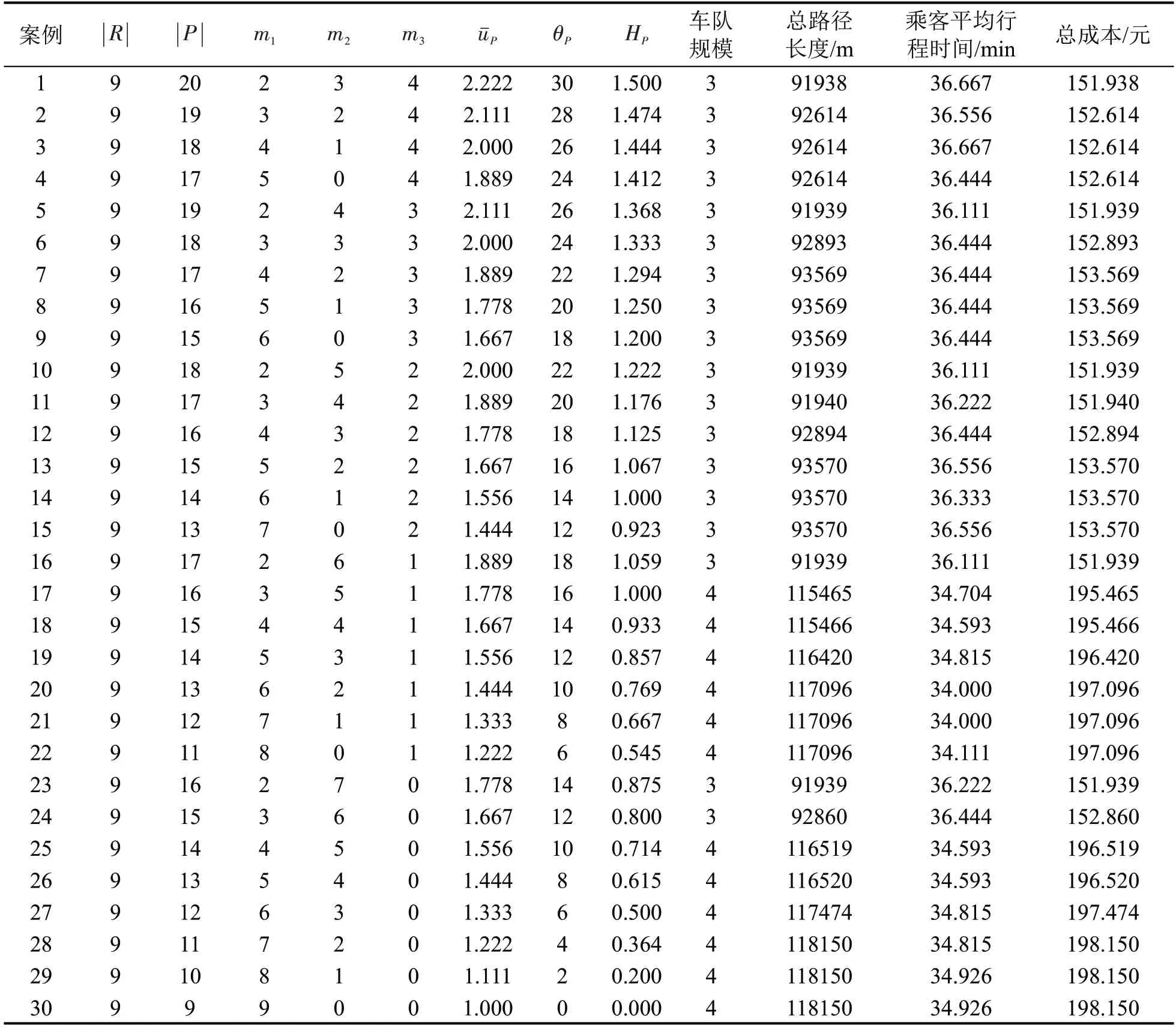
表9 候选站点对系统的影响Table 9 Effect of candidate stops on system

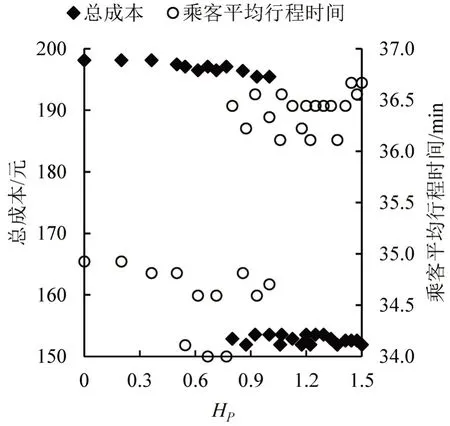
图6 候选站点对成本和乘客行程时间的影响Fig.6 Effect of candidate stops on costs and users'ride time

为进一步观察候选站点对路径细节的影响，基准案例和需求仅指定唯一上车站点的案例，即案例1 和案例30 路径的实际站点序列和实际服务的需求序列信息如表10所示。在服务相同需求的情况下，案例1使用3辆车，固定成本为60元，总路径长度为91938 m，路径成本为91.938 元，总成本为151.938 元；案例30 需4 辆车，固定成本为80 元，总路径长度为118150 m，路径成本为118.15 元，总成本为198.15元。相较于案例30，考虑候选站点的案例1 的固定成本和路径成本分别减少25%和22.19%，总成本减少了23.32%。结果表明，相较于每个乘客仅指定唯一上车站点的情况，考虑候选站点可增加需求间共乘的可能性，减少所需车辆数及总路径长度，由此带来固定成本和可变成本的降低；同时，车辆数及行驶距离的减少对于交通所带来的一系列外部问题(例如，环境污染和交通噪声等)亦有一定程度的缓解作用。

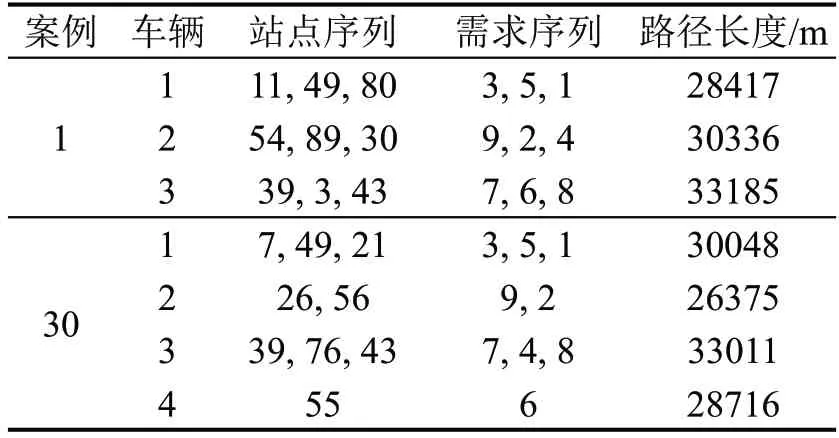
表10 有无候选站点的对比结果Table 10 Comparison results of candidate stops

3.2.3 全服务时间窗对系统的影响

为分析包含最早出发时间和最晚到达时间全服务时间窗的引入对系统的影响，本文对比实际需求量为9 的算例下含行程时间约束和单点一端时间窗约束的需求响应公交的路径优化结果。其中，行程时间的最大值由全服务时间窗的宽度(如表6的最后1列)决定，单点一端时间窗指仅指定出发或到达的时间窗，且时间窗仅指定上界(到达点的时间窗上界，即最晚到达时间，如表6 的第4 列)或下界(上车点的时间窗下界，即最早出发时间，如表6的第3 列)。以表6 为基础案例1，即需求指定最早出发时间及最晚到达时间。其余案例包含的时间约束信息如表11所示。另以需求仅指定唯一上车站点的案例30 为基础，进行时间约束的修改，如表11所示。案例的结果如表12所示，包括使用车辆数、总路径长度、总成本及乘客平均行程时间。结果表明，在需求仅指定唯一上车站点时，相较于全服务时间窗约束，单一端点的时间窗上(下)界约束或同等宽度的全服务时间窗约束下的乘客行程时间增加0.5%，车辆数减少1 辆，总路径距离减少23.3%，总成本减少24%。在需求指定多个候选站点时，相较于全服务时间窗约束，单一端点的时间窗上(下)界约束或同等宽度的全服务时间窗约束下的乘客行程时间减少5%左右，车辆总路径距离减少了约5%，总成本减少约3%，下降幅度较唯一上车站点的情况较小。原因是，基准案例中包含起点最早出发时间和终点最晚到达时间的全服务时间窗约束，暗含乘客的行程时间在全服务时间窗宽度范围内的约束。而放松其中1 个约束则可增加需求间共乘的可能性。唯一上车站点的案例30的车队规模仍有优化空间，因此，其余时间要求较为松弛的案例36～40 均实现了车队规模的减少以及总路径距离和总成本的降低。而基准案例因基准案例1中使用的车队规模已是最小值，即所有车辆均满载，所以，增加的需求共乘可能性导致车辆总行驶距离降低，从而降低乘客平均行程时间。对比站点不同情况下的不同时间要求可得，相较于仅指定唯一上车站点的情况，考虑候选站点的案例下放松时间要求所带来的成本和乘客行程时间的改善较小，由此可得，候选站点的引入弥补了全服务时间窗较紧的时间要求对路径成本和乘客行程时间的负面影响。

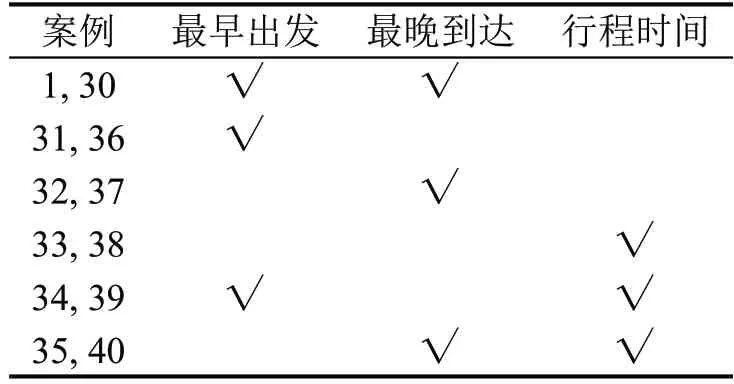
表11 不同案例的时间约束信息Table 11 Time constraints for instances

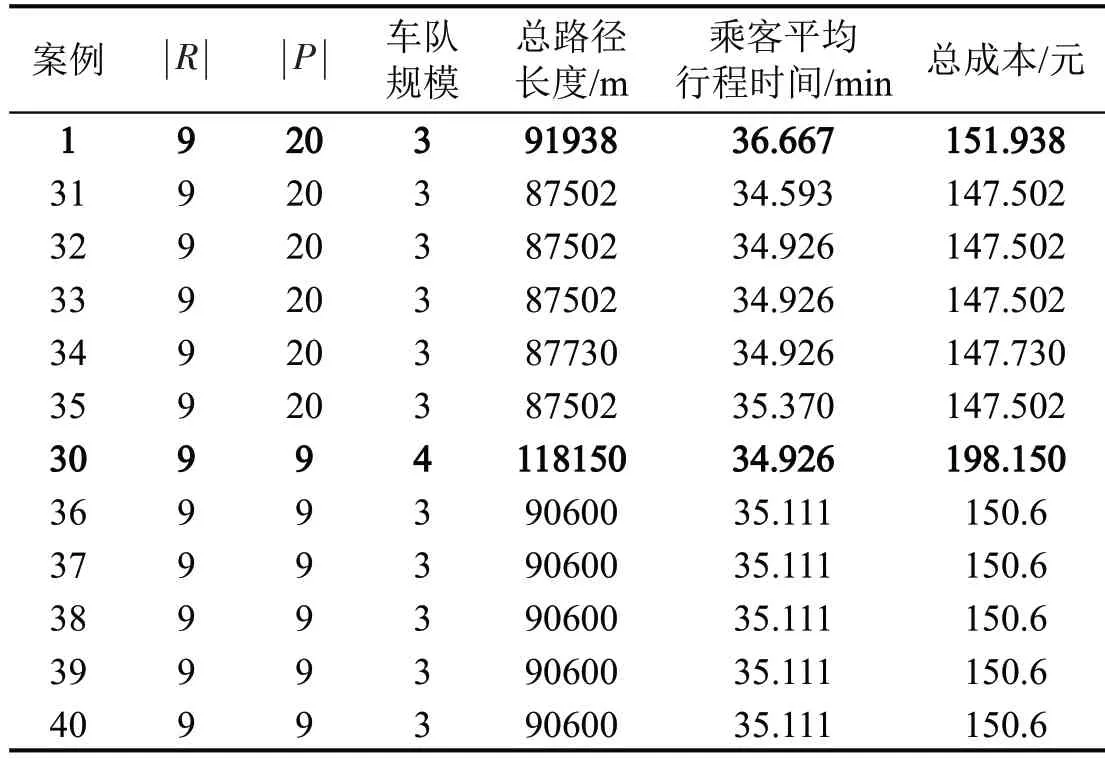
表12 不同时间约束的对比结果Table 12 Comparison results for different time constraints

4 结论

本文得到的主要结论如下。

(1)基于乘客的多个可达站点及对最早出发时间和最晚到达时间的要求，研究考虑候选站点和全服务时间窗的需求响应公交调度问题，该问题包含乘客的站点选择，车队规模的确定，及车辆路径等子问题。为降低问题维度，首先，分析站点与需求间的关系，然后，构建虚拟站点到实际需求和实际站点的映射关系，建立基于节点关系和空间距离的阻抗矩阵，将问题转化为带有全服务时间窗和容量约束的车队规模确定和车辆路径问题(FSVRP-CFSTW)模型。模型求解中，为避免因仅交换车辆编号而导致的若干重复解，增加车辆编号对称性消除约束，即考虑候选站点的车辆编号对称性消除和同站需求序列唯一性的约束，测试结果表明，该约束的引入可加速模型求解。为求解较大规模算例，基于问题特征设计多种邻域结构和基于多种邻域的自适应邻域模拟退火算法，在多规模算例下验证了该算法的效率。

(2)以广州大学城公交子网络为例，基于实际路网生成案例进行求解，验证模型及系统性能分析，并分析候选站点和全服务时间窗对系统性能的影响。结果表明：①需求的全服务时间窗和首个候选站点不变的情况下，所有需求构成的所有虚拟站点间的需求同质度的较高值可降低系统成本；②全服务时间窗相较于单点的一端时间窗和同等宽度的行程时间约束增加了路径的成本和乘客的行程时间，但考虑候选站点情况下的增幅相对唯一上车站点情况下的增幅较为微小。换言之，候选站点的引入弥补了全服务时间窗较紧的时间要求对路径成本和乘客行程时间的负面影响。