基于复杂网络的长三角和粤港澳航运网络韧性评估

王直欢，胡炜琴，王逸文

(上海海事大学，物流研究中心，上海 201306)

0 引言

港口和航运是全球贸易和供应链的基石。新冠疫情和战争等全球重大事件对航运网络的冲击，通常导致航运效率显著降低甚至中断，突显了航运网络的不稳定性和脆弱性。如何定量评估航运网络韧性和抗风险能力，有效提升航运网络应对各种风险和破坏的韧性受到了广泛关注。

韧性最早由Holling等[1]提出，主要应用于生态领域，后来不断地拓展到其他领域。Dan 等[2]从经济学角度将韧性划分为静态和动态韧性，前者指在特定时间点有效利用剩余资源的能力，而后者则可定义为系统从外部冲击中恢复的能力和速度。盛昭瀚等[3]则从供应链角度指出韧性可理解为供应链中网链结构的动力系统在遭受外界干扰时的持久力和复原力。吕彪等[4]则认为韧性是交通系统在面对扰动事件时吸收干扰并恢复的能力。航运网络韧性主要体现在航运网络中网络节点和通道抵御破坏和及时恢复的能力。

关于航运网络韧性的研究主要集中在韧性三角理论、节点失效、规划航线等方向。韧性三角理论是最常用来评估韧性的一种方法，由Holling等[1]提出，用来评价系统能力损失的程度。伍静[5]基于该理论通过韧性性能曲线构建韧性量化标准，并引入韧性—成本模型评价损失运营成本对韧性的影响，分析韧费比，得出提升韧性最需要的是重建资金。Wan等[6]在韧性三角理论的基础上用韧性成本比例衡量班轮运输网络在恢复过程的性能。Yang等[7]用可传递性和多样性来表示海上丝绸之路网络和相应节点的韧性，模拟了节点中断时网络韧性的变化。Poo等[8]通过减少气候脆弱性优化航运网络的韧性，并考虑极端天气下的航线规划问题。Yuan等[9]验证了增加一条泰国Kran 航线可以提升集装箱航线运营的韧性。

复杂网络理论通常被用于研究各类航运网络问题。Cai等[10]提出了基于复杂网络特性的航运市场动态指数计算方法；郭建科等[11]将经贸与海上丝绸之路沿线航运网络联系起来，表明不同时间段的网络均有明显复杂网络特征；许波桅等[12]构建了集装箱运输网络级联失效模型，评估网络的鲁棒性。然而，航运网络韧性研究通常侧重于为频繁和可观察到的中断做好准备，而较少关注尚未发生的不可预测事件。不可预测的破坏事件在空间和时间上是不可预测的，在性质上是未知的，甚至是随机的。

为此，本文构建一种在不同破坏情景下定量评估港口群航运网络韧性的方法，破坏模式包括度破坏(Degree Attack,DA)、中间性破坏(Betweenness Attack,BA)、强度破坏(Strength Attack,SA)、随机破坏(Random Attack,RA)。长三角和粤港澳是我国经济最为发达和活跃的两个地区，它们的运行状态对于我国乃至全球经济的发展具有重要影响。然而，当前全球航运环境不断变化，不确定性因素增加，这两个航运网络可能面临重大的风险挑战，但较少有学者关注到它们的韧性和抗风险能力。因此，本文以长三角和粤港澳港口群内部航运网络为研究对象，利用真实数据评估两个港口群在不同攻击模式下的韧性水平，旨在为提升港口群航运网络韧性提供理论依据。

1 评估方法

本文将航运网络韧性评估过程划分为4 个阶段，分别为初始、破坏、恢复和稳定阶段，根据网络节点港口的度值、中间性、强度从大到小对节点排序，模拟网络节点的中断和恢复过程，并选取网络独立路径数、网络效率、网络连通度这3个指标，分析并提出相应的优化策略。模拟过程中，攻击一个节点或恢复一个节点可看作时间推进一次。评估框架如图1所示。

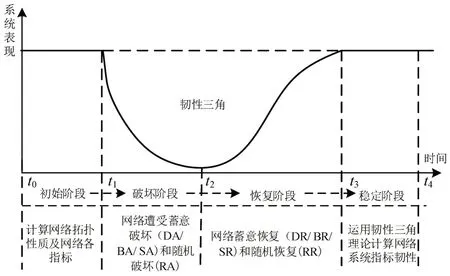
图1 航运网络韧性分析框架[13]Fig.1 Framework of shipping network resilience

各阶段具体步骤如下。

①初始阶段(t0～t1)

t0为航运网络尚未被破坏的初始时间点，初始阶段持续到t1，t1时刻网络遭到破坏。在该阶段内计算航运网络中港口节点基本拓扑性质，度、中间性、强度，以及网络韧性指标，即网络独立路径数、网络效率、网络连通度。

②破坏阶段(t1～t2)

用以下两种攻击方式破坏网络节点：蓄意攻击，分别根据网络节点拓扑性质从大到小排序，依次删除节点，即度破坏、中间性破坏、强度破坏，继而计算网络独立路径数、网络效率、网络连通度的变化；随机攻击，随机破坏即随机删除节点，模拟200 次随机序列攻击，并在该时间点对该破坏模式下的网络指标取200次的平均值。在t2时刻，网络的网络独立路径数、网络效率、网络连通度在下一个时间点为0，此时3 个指标的数值为最小值。该阶段包括度破坏、中间性破坏、强度破坏以及随机破坏这4种破坏模式。

③恢复阶段(t2～t3)

在节点被破坏后，按以下两种方式恢复节点：蓄意恢复，按网络节点的性质从大到小恢复节点，即度恢复(Degree Recovery,DR)、中间性恢复(Betweenness Recovery,BR)、强度恢复(Strength Recovery,SR)；随机恢复(Random Recovery,RR)，模拟200 次随机序列取平均值。分别计算网络独立路径数、网络效率、网络连通度随之发生的变化。在t3时刻，网络的网络独立路径数、网络效率、网络连通度恢复到初始值。该阶段包括度恢复、中间性恢复、强度恢复以及随机恢复这4 种恢复模式。

④稳定阶段(t3～t4)

稳定阶段可持续到t4，在该阶段基于韧性三角理论计算各网络系统指标韧性，即网络独立路径数、网络效率、网络连通度的韧性。

评估过程中涉及的拓扑属性及指标计算方式如下。

(1)度值

节点Vi的度值可以用与之相连的节点数目表示。港口的度值越大说明经过该港口的航线数目越多，影响力越大。入度可以反映港口的直接可达性，出度则能反映港口与其他港口建立联系的直接能力。

(2)中间性

存在不直接相连的两个节点Vj和Vl，连接两点的最短路径会经过某些节点，多条路径都经过Vi，则表明Vi在网络中的中间性较强，节点中间性越强，其在航运网络中的通达能力越好。

(3)强度

节点Vi的强度由周围相邻节点的权重累加来决定。

(4)网络独立路径

网络节点的总数为n，如果路径集合中包含节点对之间的所有连接路径，节点对的数量为n(n-1)，且路径之间没有相同的边，则该集合是节点之间的独立路径集。独立路径值可以用来衡量网络通道的多样性。网络独立路径数可表示为

式中：G为Vi的邻接节点集；Iij(t)为在时间t时刻节点Vi与Vj之间独立路径的条数。

(5)网络效率

网络效率可反映网络节点的韧性，节点间距离更近时节点间传输将更容易，因此节点对之间的效率被定义为节点间最短路径长度的倒数的累加，网络全局效率为所有节点对效率的平均值，取值范围在0～1之间，表示为

式中：dij(t)为在时间t时刻节点Vi与Vj之间最短路径长度。

(6)网络连通度

网络连通度为最大连通子图中的节点数与原始网络中的节点总数之比，即

式中：m(t)为在时间t时刻最大连通子图中节点数量。

(7)韧性指数

韧性三角理论是指可通过提高系统性能，或缩短恢复时间，减小韧性三角形面积。在系统性能初始值确定的情况下，韧性指数R越大，作为分子的系统性能在破坏和恢复的时间进程中曲线积分就越大，较之初始系统性能指标的损失越小，即在该区间内的韧性三角形面积越小，则该网络的韧性也就越大。赵雪婷等[14]在研究公路网络时引入时间纬度表达交通网络韧性，鉴于此，本文韧性指数可由网络经历破坏和恢复过程中系统表现随时间变化的恢复程度来表示，即

在本文中，图1纵轴的系统表现选取了航运网络的网络独立路径、网络效率和网络连通度这3个纬度来度量，计算网络受到破坏并恢复过程中每个时刻三者的具体取值，形成系统表现曲线，进而计算韧性指数。

2 实例分析

2.1 初始阶段长三角和粤港澳航运网络性质

为了能够反映当前航运网络的最新动态，本文从第三方数据提供商获取2023 年1 月～6 月的全球船舶挂靠数据，并针对每条船舶的挂靠数据按照时间顺序排列，得到所有船舶的航线信息。由于本文主要关注长三角和粤港澳两个港口群内部航运网络的韧性水平，故只保留起始港和目的港都在港口群内部的航线。在此基础上，本文以长三角和粤港澳航运网络中的港口作为网络节点，两个港口间的航线作为网络的边，通航次数作为权重，分别构建两个港口群的有向航运网络。由于长三角和粤港澳航运网络基于真实航行轨迹构建，因此，并不一定所有的边都是双向的，如有些边由于通航条件和航道等原因有可能是单向的。

长三角内部航运网络如图2所示，包含58个节点，将度值、中间性、强度排名前9的港口去重后的港口名称于图中显示。长三角前9个港口的度值、中间性、强度如表1 所示，宁波舟山港占有四席。其中，舟山港和北仑港的度值最高，如皋港和舟山港的中间性位列第1和第2。舟山港和洋山港的强度最大。粤港澳内部航运网络如图3所示，有25个节点，仅显示了度值、中间性和强度前9 去重后的港口名称。粤港澳前9 个港口的港口度值、中间性、强度如表2所示。维多利亚港和南沙港的度值最大，东莞港和虎门港的中间性最大，维多利亚港和赤鱲角强度遥遥领先。

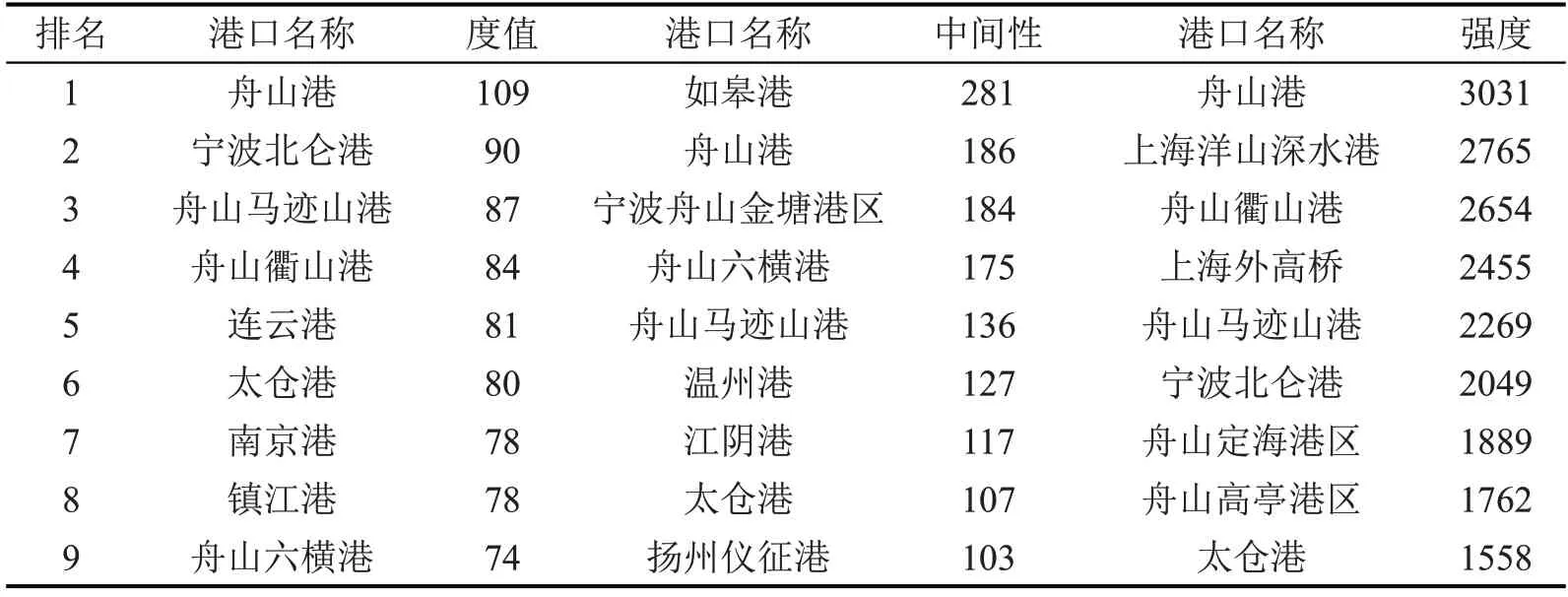
表1 长三角内部航运网络节点港口TOP 9Table 1 Node of Yangtze River Delta internal shipping network TOP 9

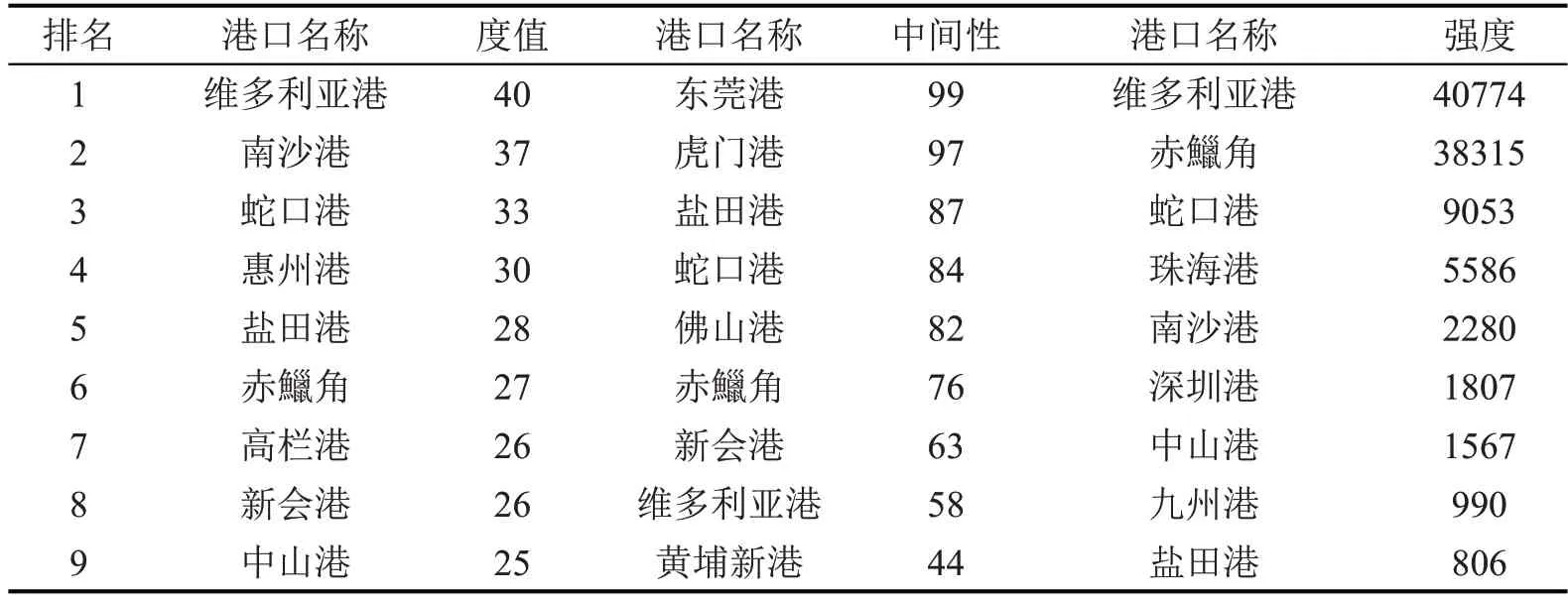
表2 粤港澳内部航运网络节点港口TOP 9Table 2 Node of Guangdong-Hong Kong-Macao internal shipping network TOP 9

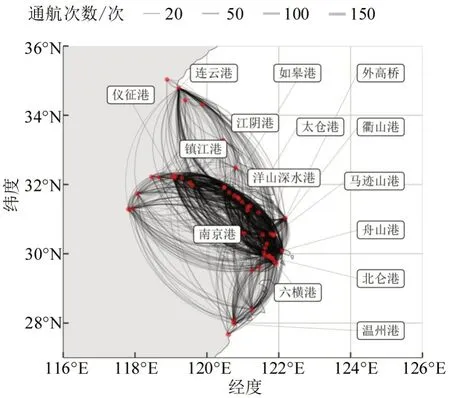
图2 长三角内部航运网络图Fig.2 Yangtze River Delta(YRD)internal shipping network diagram

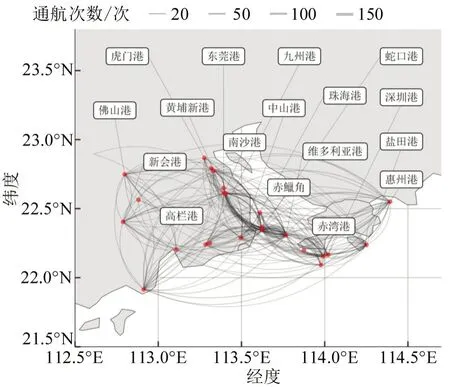
图3 粤港澳内部航运网络图Fig.3 Guangdong-Hong Kong-Macao(GHM)internal shipping network diagram

初始阶段，长三角航运网络的网络效率为0.496，网络独立路径数为16.427。粤港澳航运网络的网络效率为0.376，网络的独立路径数量为6.293。两者的网络连通度均为1。长三角航运网络的网络效率和独立路径数量高于粤港澳航运网络，且网络独立路径数反映的是网络通道的多样性，即便某个港口节点被破坏，还可以选择其他连通的路径，故长三角网络抵抗风险的能力更好。

2.2 破坏阶段长三角和粤港澳航运网络分析

图4 为长三角航运网络和粤港澳航运网络在遭到破坏时各个指标的变化情况。默认在网络指标值下降到0 时，破坏阶段得以结束。图中第1 行描绘了长三角航运网络韧性指标在受到BA、DA、RA、SA 时随被破坏节点个数增多的动态变化，从左到右的指标依次为网络效率、网络连通度、网络独立路径。第2 行是粤港澳航运网络对应指标的变化情况。

图4 4种破坏模式下长三角与粤港澳航运网络指标Fig.4 Indicators of YRD&GHM shipping network under four destruction mode

由图4可知，长三角航运网络和粤港澳航运网络遭受RA 攻击时，各项指标都下降得最缓，在RA模式下两个网络有较好的抵抗力。

长三角航运网络的网络连通度曲线在不同攻击模式下重合度较高，差异不明显，这是因为其随着节点被破坏，最大联通子图的节点数下降幅度接近线性。

粤港澳港口群的网络效率值在SA模式中出现了较大波动，这是因为粤港澳港口群港口节点较少。网络遭受破坏过程中，网络节点间的最短路径长度相对固定，但节点对的个数下降较快，因此造成了网络效率值回升较大的现象。

港口群航运网络各个指标在不同攻击模式下的表现差异较大。网络效率在受到BA攻击模式时下降地最快，抵抗攻击的能力最差。网络独立路径数和网络连通度在遭受DA 攻击模式时下降得最快，表明中间性和度值大的节点越先遭受攻击，对网络的破坏性越大。

比较网络各指标在不同模式中下降的百分比可知，长三角航运网络和粤港澳航运网络对破坏的吸收能力接近。长三角航运网络遭受破坏后，网络效率、网络独立路径数、网络连通度最小值分别为0.012、0.133、0.017，与初始网络相比，分别下降了97.43%、99.18%、98.27%。粤港澳航运网络的网络效率、网络独立路径数和网络连通度分别为0.010、0.066、0.040，3个指标对应下降了97.09%、98.94%、96.00%。长三角和粤港澳航运网络在遭到破坏前后3个网络指标下降的百分比相差不大，长三角略高于粤港澳，故两个网络吸收破坏的能力差距不大。

2.3 恢复阶段长三角和粤港澳航运网络分析

图5 和图6 从左到右均为航运网络的网络效率、网络连通度、网络独立路径数在对应DA、SA、BA、RA 破坏模式下以DR、SR、BR、RR 这4 种模式恢复得到的变化曲线。恢复阶段被定义为从网络各个指标趋于0前的一个时间点开始恢复，仅在计算网络连通度时，从此时的前一个时刻开始恢复网络，因为在该时刻删除节点后整个网络中只存在孤立的点而构不成网络。并且恢复在这里被定义为，如果节点恢复，则与之相连的节点和路径也同时恢复。长三角航运网络各指标的表现如图5所示，粤港澳航运网络各指标的表现如图6所示。

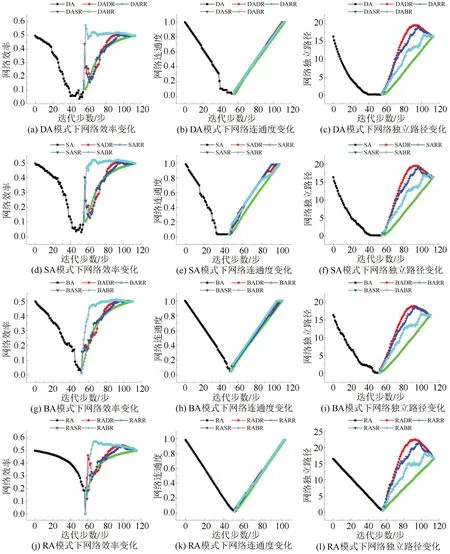
图5 4种恢复模式下长三角的网络指标Fig.5 Network indicators of YRD under four recovery models

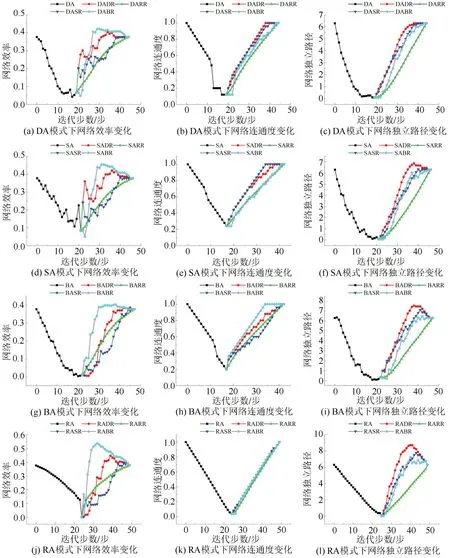
图6 4种恢复模式下粤港澳的网络指标Fig.6 Network indicators of GKM under four recovery models

长三角航运网络的网络效率在BR模式下恢复得最快，为恢复网络效率，可优先恢复中间性最大的，如皋港、舟山港。其网络独立路径数在DR下恢复得更快，不同恢复模式下网络独立路径数的曲线也比网络效率和网络连通度要平滑。为更快地恢复网络独立路径数，长三角航运网络可优先恢复度值大的港口，如宁波舟山港和宁波北仑港。

粤港澳航运网络的网络连通度在RR模式下恢复得最慢，且以RR 模式恢复被RA 模式破坏的韧性三角最大，网络韧性最差。粤港澳航运网络的网络效率恢复情况受不同恢复模式的影响较大，仍以BR 恢复最快，可优先恢复中间度居于前二的东莞港和虎门港。其网络独立路径数以DR 恢复最快，可优先恢复度值位于前列的维多利亚港和南沙港以恢复通道多样性。

在两个网络遭到RA 攻击后开始恢复的过程中，网络独立路径值和网络效率值均出现比初始值还大的情况，这是因为当网络按照SR、BR、DR 恢复时，一些枢纽节点先恢复了，这些枢纽节点与其余节点加强了连接，网络得以更快恢复，因此网络指标在一个阶段超过了原值，之后一些外围节点再恢复时，与之相连节点数较少，指标值随之下降。而网络效率受到RA破坏后按BR恢复时曲线波动较大，其原因和节点受到破坏时类似，刚开始恢复时节点对增加的速度不及路径的恢复速度，故达到了峰值。

总体上，网络效率按不同模式恢复时表现出的差异最大，而网络连通度表现得差异较小。此外，粤港澳网络的各个指标恢复到初始值的时间点差异更大，即同一个指标的子图中不同模式恢复到原值的迭代步数不一，而长三角网络指标在不同模式下恢复到初始值的时间点是趋近的，一定程度上说明，粤港澳的航运网络对破坏和恢复的模式更敏感。

2.4 稳定阶段长三角和粤港澳航运网络韧性

航运网络经历上述破坏恢复过程后，利用韧性三角理论量化网络各指标受损程度，得到长三角和粤港澳航运网络韧性对比如图7所示。

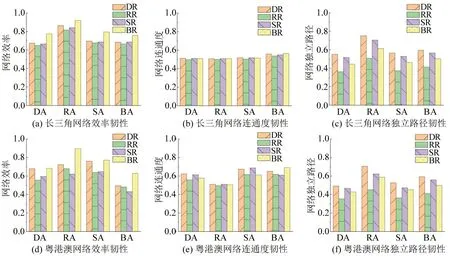
图7 长三角和粤港澳内部航运网络韧性对比Fig.7 Comparison of internal shipping network resilience in YRD&GHM

图7中第1行从左到右分别为长三角航运网络的网络效率、网络连通度、网络独立路径，第2行则为对应的粤港澳航运网络韧性指标。将恢复阶段得到的曲线分别代入韧性指标式(4)～式(6)中，以图7(a)为例，攻击模式为横坐标，从左往右柱形代表DADR、DARR、DASR、DABR 等模式下网络效率的韧性值。

观察韧性值可知，网络独立路径和网络效率受到RA攻击时韧性最好，3个指标按RR恢复时韧性几乎都是最差的。并且，网络效率的韧性相比网络连通度、网络独立路径更高，这也反映在恢复过程中，网络效率的恢复曲线最陡，恢复得最快，韧性三角的面积也最小。从整体上来看，两个网络受到特定模式攻击后再以不同模式恢复的韧性在图中相对趋势上的差别较小，但韧性绝对值仍有一定差距。长三角航运网络独立路径在不同模式下的韧性之和为8.452，网络效率为11.863，网络连通度为8.319；粤港澳航运网络的独立路径、网络效率、网络连通度数值分别为7.986、10.298、9.562。粤港澳航运网络的网络连通度韧性要优于长三角航运网络，长三角航运网络的网络独立路径韧性和网络效率韧性优于粤港澳航运网络。

由图7可知，长三角航运网络和粤港澳航运网络受到DA攻击后以，多种模式恢复的韧性较其他攻击模式均较差，长三角可优先保障宁波舟山港、北仑港等度值较大港口的连通能力，而粤港澳网络遭受攻击后，其网络连通度以SR或DR模式恢复韧性较好，应对强度和度值均最高的维多利亚港进行保护。

3 结论

本文基于复杂网络和韧性三角理论，提出了定量评估港口群航运网络韧性的方法。以长三角内部航运网络和粤港澳内部航运网络为例，选取2023年上半年全球船舶挂靠数据，通过模拟两个港口群网络在4 种破坏模式和恢复模式下网络独立路径数量、网络效率、网络连通度的动态变化评估其韧性水平，主要结论如下：

(1)提供了一种基于船舶真实航行数据，定量评估航运网络在不同攻击情景下韧性水平的方法，表明网络独立路径数、网络效率、网络连通度指标和对不同破坏并恢复模式的模拟可以适用于不同类型和规模的航运网络，为评估和改善航运网络的韧性水平和抗风险能力提供了工具。

(2)长三角内部航运网络初始阶段网络独立路径数高于粤港澳，其航线通道更具多样性，抗风险能力更强。破坏阶段长三角航运网络遭受破坏后网络各指标下降的百分比和粤港澳航运网络相对应的数值接近，两者吸收破坏的能力接近。长三角等规模较大且港口强度分布均衡的港口群，其航运网络的效率和网络独立路径数分别在BR和DR模式下恢复得最快，可优先恢复中间性最大的港口(如皋港)和度值最大的港口(如宁波舟山港)。

(3)粤港澳内部航运网络恢复阶段的网络效率和网络独立路径数在恢复效率上与长三角航运网络表现类似，网络连通度以SR或DR模式恢复韧性较好，粤港澳等港口较集中，枢纽港口强度突出的港口群，可优先恢复强度和度值较高的港口，如维多利亚港。

(4)总体上粤港澳内部航运网络的网络连通度韧性要优于长三角内部航运网络，长三角的网络独立路径韧性和网络效率韧性优于粤港澳航运网络。并且，两者受到DA攻击后再以其他模式恢复的韧性较差，粤港澳航运网络可优先保护度值大的维多利亚港和南沙港，长三角航运网络则着重保障宁波舟山港和北仑港的连通效能。