基于油中溶解气体分析的ISSA优化LSSVM变压器故障诊断研究

李雷军, 吴 超, 付 华, 齐 致, 王久阳

(1. 辽宁工程技术大学电气与控制工程学院, 辽宁 葫芦岛 125105; 2. 中国科学院电工研究所, 北京 100190; 3. 国网葫芦岛供电公司, 辽宁 葫芦岛 125105)

1 引言

电力变压器是电网中至关重要的设备,在输送电过程中起升、降压的作用,整个供配电系统的安全直接受到变压器性能的好坏影响,一旦发生故障,将会对电力系统的正常运行造成严重威胁,因此研究变压器故障诊断方法对电力系统稳定运行有重要意义[1-3]。

目前,油浸式电力变压器在输配电系统中被广泛采用。在变压器故障诊断当中,基于变压器油中溶解气体分析(Dissolved Gas Analysis, DGA)技术被普遍应用[4]。随着人工智能的发展,通过结合智能算法的诊断方法,有效地利用DGA技术,变压器故障诊断的准确率得到了显著提高,如神经网络[5]、支持向量机[6](Support Vector Machine, SVM)、极限学习机[7](Extreme Learning Machine, ELM)等方法被广泛应用,如文献[8]采用基于油的气体分析技术,通过改进的灰狼优化器来优化概率神经网络(Probabilistic Neural Network, PNN)模式层的平滑因子,以提升PNN的鲁棒性和分类准确度。文献[9]则提取了变压器的不同振动信号,并通过主成分分析将其映射到二维图像中,通过K近邻(K-Nearest Neighbor, KNN)实现了故障的分类和识别。结果表明,该方法自动模式识别效果较好。文献[10]通过无编码比值法获得了油中的9维特征向量,之后使用核主成分分析(Kernel Principal Component Analysis, KPCA)进行预处理,然后,采用改进的鲸鱼优化算法对SVM模型进行了优化,用于变压器故障诊断。实验结果表明,所构建的模型具有高精度和强稳定性的特点。文献[11]基于实验采集的油样进行了研究,提出了KPCA-ELM模型,并利用激光诱导荧光光谱技术,快速诊断电力变压器是否存在故障。实验结果表明,所提出的方法能够有效地确保电力设备的安全运行。尽管上述方法在变压器故障诊断方面提高了诊断精度,但仍有各自局限性,如人工神经网络系统复杂,不易收敛;极限学习机训练过程中具有不稳定性;SVM本身是二分类器,对于变压器的多分类问题,存在分类效果不佳的问题。相较于以上方法,最小二乘支持向量机[12](Least Square Support Vector Machine,LSSVM)具有计算速度快、泛化能力强、能解决变压器非线性样本分类问题等优点,但是其分类效果由惩罚参数 和核函数参数决定,同时,变压器的故障数据呈现出非线性的特点,维数过高且复杂,容易加大变压器故障诊断难度。因此可采用维度约简算法对原始数据进行预处理,避免信息之间的相关重叠。以预处理后的数据作为诊断依据,以LSSVM进行变压器故障诊断的关键是如何找到合适的参数值,成为相关学者研究的重点。群体智能寻优算法的广泛应用表明可以有效解决参数寻优问题。通过樽海鞘领导者和追随者的觅食行为,樽海鞘群算法(Salpa Swarm Algorithm,SSA)实现了局部搜索。虽然该方法对大部分工程问题具有优越性,但该方法的缺点是收敛速度较慢,容易陷入局部极值。

鉴于以上分析,提出一种基于等规度映射算法 (Isometric mapping, Isomap)和改进樽海鞘群算法优化最小二乘支持向量机的故障诊断方法。首先Isomap算法对原始数据进行预处理,去除冗余数据。然后采用经半数均匀初始化、混合反向学习以及引入非线性递减的惯性权重因子改进的SSA来优化LSSVM的参数,最后与传统的SSA、粒子群算法(Particle Swarm Optimization,PSO)、正弦余弦算法(Sine Cosine Algorithm,SCA)优化的LSSVM故障诊断模型进行变压器故障诊断精度对比分析,验证所提方法的优越性。

2 基于Isomap的特征量提取方法

在传统的电力变压器故障诊断中,研究者常常忽视了高维度的原始数据对变压器故障诊断精度产生的影响。因此,本文选择采用Isomap方法来提取变压器故障样本数据的特征,有效剔除影响模型诊断精度的冗余信息,以提高变压器故障诊断精度。

Isomap是一种基于邻域图和多维尺度分析(Multi Dimensional Scaling,MDS)的流形算法[13,14],通过建立原数据间测地距离代替欧式距离作为样本点间的相似性度量,更能反映真实的流形低维结构[15]。Isomap算法过程如下:

(1)构建邻域图G。设定变压器样本数据个数为n,高维空间样本集为X={xi|i=1,2,…,n},X∈RN。计算任意样本xi和xj的欧式距离de(xi,xj),当xi和xj间距离小于i和j的k-邻域时,则认定xi和xj相邻,线连接邻近点,建立高维数据的带权邻域图G,其中G的边为邻边eij的权值,长度等于xi和xj的欧式距离de(xi,xj)。

(2)计算邻域图G中测地距离dG(xi,xj)。根据弗洛伊德算法或迪杰斯特拉算法测量任意两样本xi和xj之间的最短距离dE(xi,xj),若xi和xj之间存在连线,则dG(xi,xj)的初始值为dE(xi,xj),否则令dG(xi,xj)=∞。对于全部的k(k=1,2,…,n),有:

dG(xi,xj)=min{dG(xi,xj),dG(xi,xk)+dG(xk,xj)}

(1)

式中,DG为测地距离矩阵,DG={dG(xi,xj)},它是由图G中所有点的最短路径组成的。

(3)构造d维嵌入。MDS方法应用于式(2)中的矩阵DG,最小化目标函数以获得低维坐标Y。

(2)

(3)

式中,τ(DG)为操作矩阵算子;DY为降维后样本点间的欧氏距离矩阵;H为单位矩阵;H*为H的伴随矩阵。特征分解τ(DG),取前d个特征值λ1,λ2,…,λd和特征向量V1,V2,…,Vd,构造一个保留原数据特征的d维嵌入。

由上述分析可知,采用Isomap方法对变压器故障原始数据进行特征提取需近邻点数k和低维空间维数d。k值偏大会增加模型的运行时间,k值偏小会导致正常数据被算法当成异常值舍去。

3 改进樽海鞘群算法

3.1 SSA算法

樽海鞘群算法[16,17]是通过模拟樽海鞘生物在海中航行和觅食行为提出的樽海鞘链模型。通过个体间相互协作追踪移动的食物源,使樽海鞘群算法逼近全局最优。SSA模型描述如下:

(4)

式中,N为种群数目;D为空间维数;ubj、lbj分别为搜索空间上界、下界;rand()为随机函数。

领导者的位置更新如式(5)所示:

(5)

(6)

式中,Tmax为最高迭代次数。

追随者在位置更新时,移动的距离R可以依据牛顿定律如下所示:

(7)

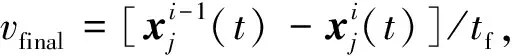
因此,追随者的位置更新公式为:

(8)

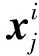
3.2 SSA算法的改进

樽海鞘群优化算法在求解很多工程问题上具有良好的特性,同时也存在着收敛精度较低、容易陷入局部最优解的问题。为了提高变压器诊断精度,提出半数均匀初始化、混合反向学习、非线性递减权重的策略来对樽海鞘群算法进行改进,提升其收敛精度和收敛速度。

3.2.1 半数均匀初始化

在个体初始化阶段,SSA算法只能保证种群位置的分散程度,而分散并不意味着均匀,因此提出半数均匀初始化[18]策略提高种群多样性,即种群前半部分个体随机初始化,后半部分在均数区间内初始化。将搜索空间分成N/2个子空间,再将个体初始解在相应子空间内随机初始化。该初始化方式能保留种群随机性,还能避免分布密集,有利于提高种群多样性,可在一定程度上避免出现局部极值。

半数初始化策略数学模型为:

(9)

式中,xu、xl分别为上、下限区间向量;xi(t)、xj(t)为个体初始值,其中i=1,2,…,N/2,j=N/2+1,…,N。

3.2.2 混合反向学习策略

SSA算法存在着容易陷入局部最优解和过早收敛的问题,而改善随机优化算法陷入局部最优解的有效途径是采用反向学习[19,20](Opposition-Based Learning,OBL)方法,其通过评估当前可行解和反向解,并选择最优解进入下一次迭代。因此提出一种透镜成像反向学习,结合最优最差反向学习的机制,寻找两个可行解,并对其进行反向解求取,用此机制对SSA进行改进,提高其收敛精度。

(1)透镜成像反向学习策略

透镜成像反向学习策略应用于当前最优个体上,会产生新的个体,增加种群中樽海鞘位置的多样性,可增强SSA算法的全局勘探能力。

假设个体P的高度为h,其在x轴上的投影为x*,x*即为最优个体,在寻优范围[a,b]的中心点放置焦距为f的透镜,通过透镜成像原理得到像P′,其高度为h′,在x轴上的投影为x′*,x′*即为x*的反向解,如图1所示。

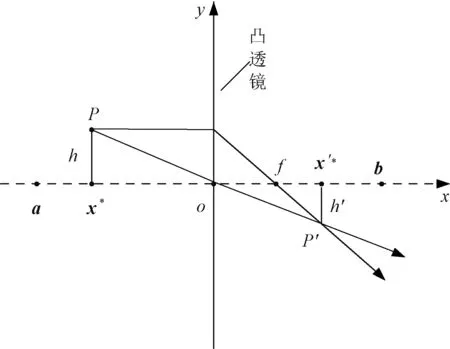
图1 基于透镜成像的反向学习策略示意图Fig.1 Opposition learning strategy based on lens image

由透镜成像原理可知:

(10)

令h/h′=s,s为缩放因子,变换式(10)得到反向点x′*的计算公式为:

(11)

当s=1时,式(11)可转化为:

x′*=a+b-x*

(12)

式(12)为作用在x*上的一般反向解,一般反向学习策略是透镜成像学习策略的特例,得到新候选个体,若想新候选体为动态,则调整s即可。将式(12)反向学习策略推广到D维空间得到:

(13)

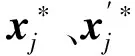
(2)最优最差反向学习策略

增加樽海鞘位置在种群中的多样性,提升算法在整个范围内的搜索能力,最优最差反向学习是一种有效机制,因此,采用随机反向学习的策略来处理全局最差位置的樽海鞘个体,其公式为:

XWorst(t+1)=aj+r·[bj-XWorst(t)]

(14)

式中,XWorst为每一代的全局最差位置;r为[0,1]上的随机数。

SSA算法都通过式(13)、式(14)进行位置的更新与筛选,将适应度值设定为以变压器故障诊断准确率为标准,若新适应度值大于之前适应度值,则更新全局最优解。选择当前种群中表现最佳和最差位置个体进行处理,在式(14)中,aj和bj是动态变化的,其能准确搜索,有效提高算法的寻优精度。

3.2.3 非线性递减的权重因子

在SSA算法中,由追随者位置更新式(8)可知,在保持自身特征的同时,追随者会向前一个个体的位置移动,完成位置更新,这样的位置更新方式较为单一,如果领导者在局部极值中无法逃逸,则追随者必然会追随至此区域。为了提升跟随者位置更新机制的灵活性和有效性,引入一种非线性递减的惯性权重,以衡量前一个个体对当前追随者的影响程度[21]。改进后的追随者位置更新公式如下:

(15)

非线性递减惯性权重如下:

(16)

式中,δ为本文设计的非线性惯性权重,如图2所示;δinitial、δfinal分别为初始的惯性权重和最终的惯性权重;ε为大于0且极小的数;Tmax为最大迭代次数。非线性的惯性权重因子δ在迭代前期依然保持较大值可避免跟随领导者陷入局部极值区域,后期下降速度较快可增强其收敛速度,相较于线性的权重因子,它更能协调全局探索和局部开发的平衡。

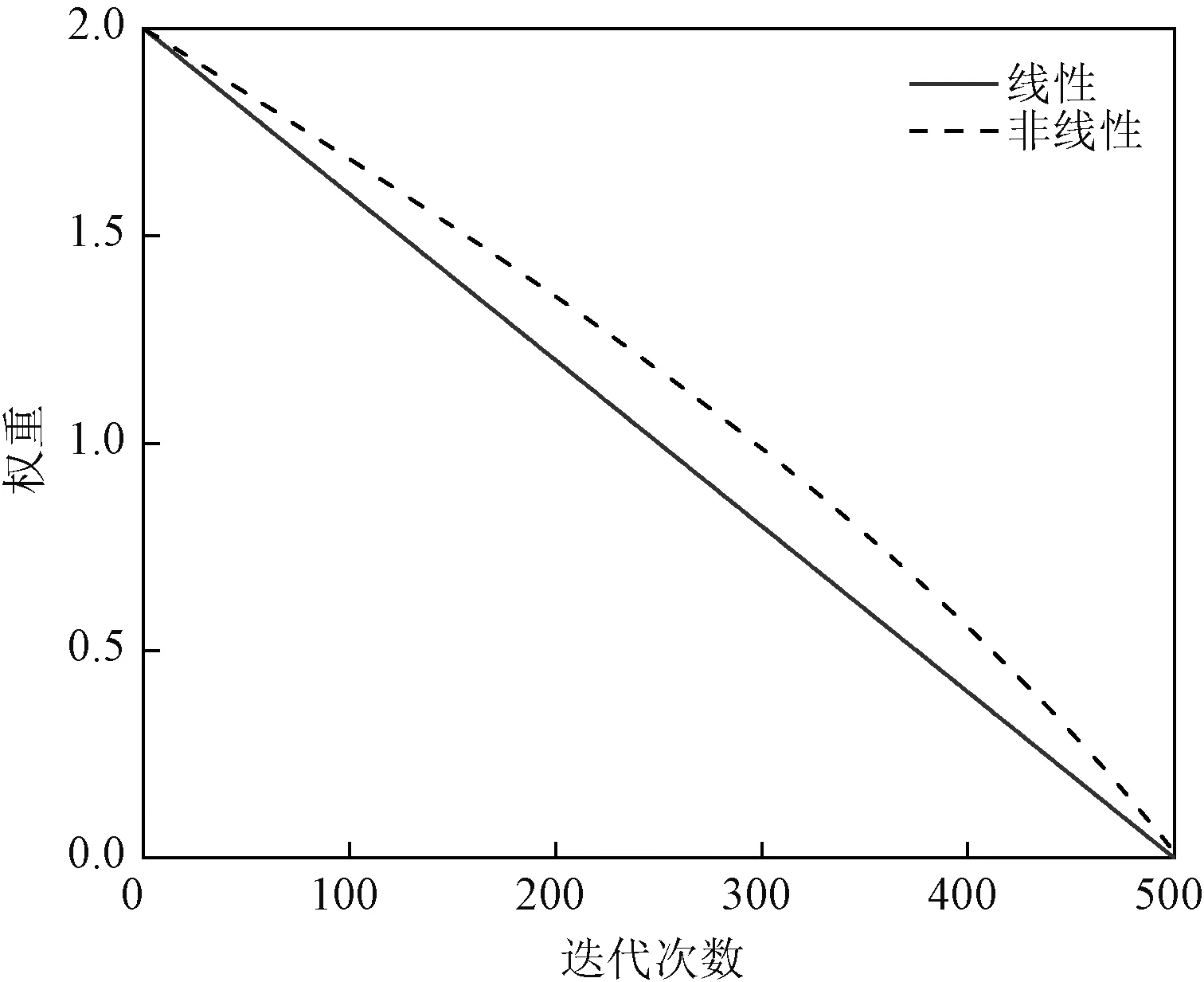
图2 线性与非线性权重因子示意图Fig.2 Schematic diagram of linear and nonlinear weight factors

3.3 算法性能测试

基准测试函数是评价算法的有效性、稳定性和可行性的重要方法,为验证上述改进樽海鞘优化算法(Improved Salpa Swarm Algorithm ,ISSA)的有效性,选取5种测试函数进行性能测试,用于测试函数寻找全局最优的能力和测试算法的局部开发能力。测试函数及其具体信息见表1。

表1 5种基准测试函数Tab.1 Five benchmarking functions

将改进的SSA算法和原始SSA、PSO和SCA算法进行比较,在Matlab中进行仿真实验,仿真实验结果见表2、表3,寻优流程如图3～图7所示。

表2 相同迭代次数(500次)算法寻优结果Tab.2 Optimization results of algorithm for same number of iterations (500)

表3 相同收敛精度(10-6)算法迭代次数(限定最大500次)Tab.3 Number of iterations of algorithm with same convergence accuracy (10-6)(limited to a maximum of 500 iterations)

图3 f1函数寻优曲线Fig.3 f1 function seeking curve

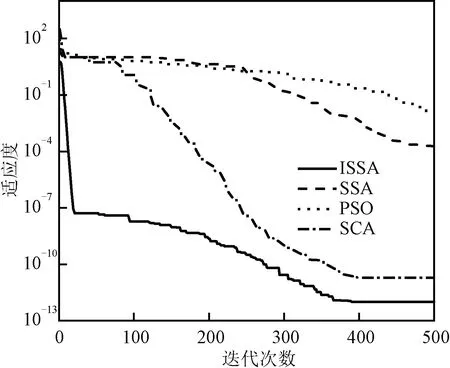
图4 f2函数寻优曲线Fig.4 f2 function seeking curve

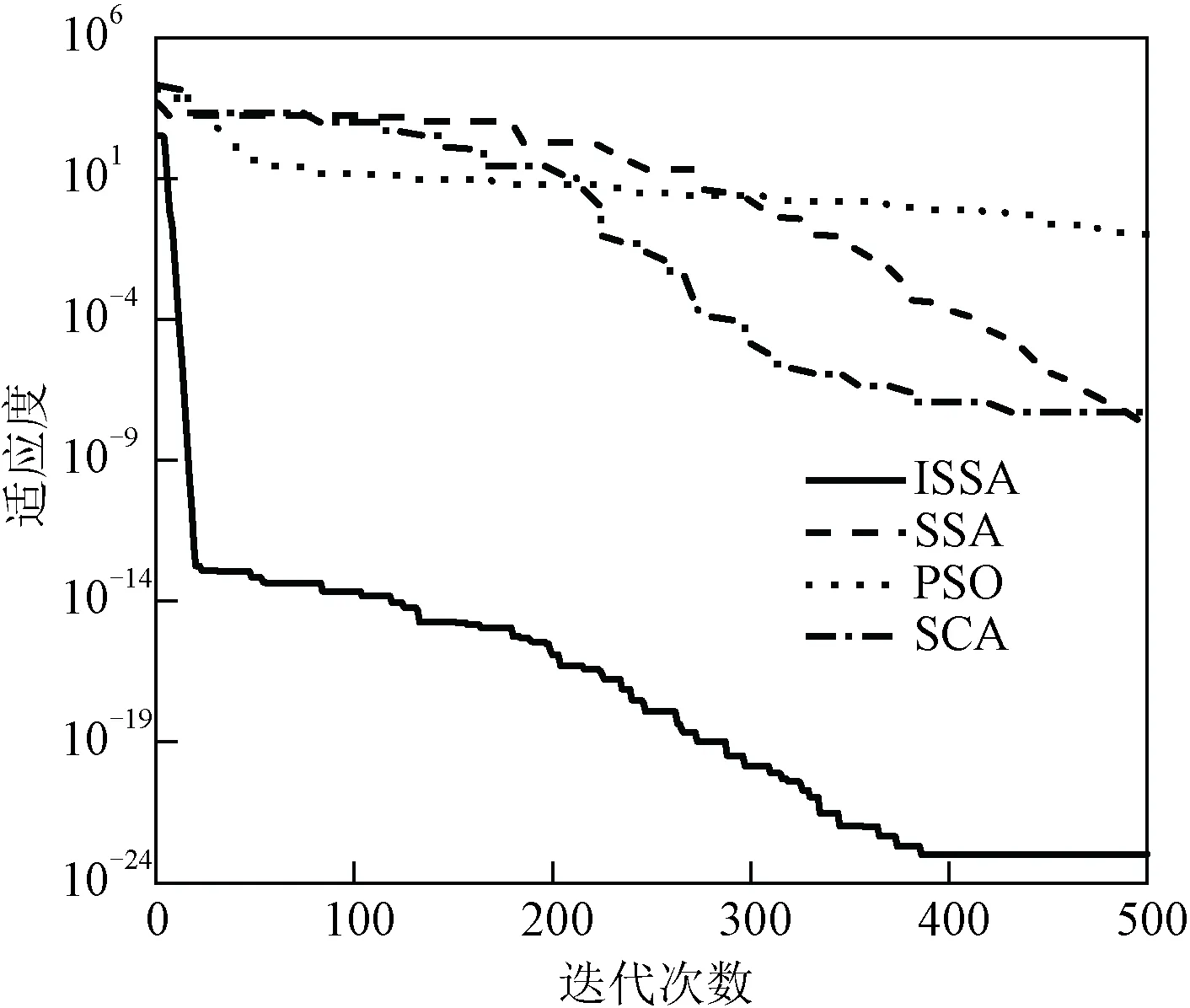
图5 f3函数寻优曲线Fig.5 f3 function seeking curve

图6 f4函数寻优曲线Fig.6 f4 function seeking curve

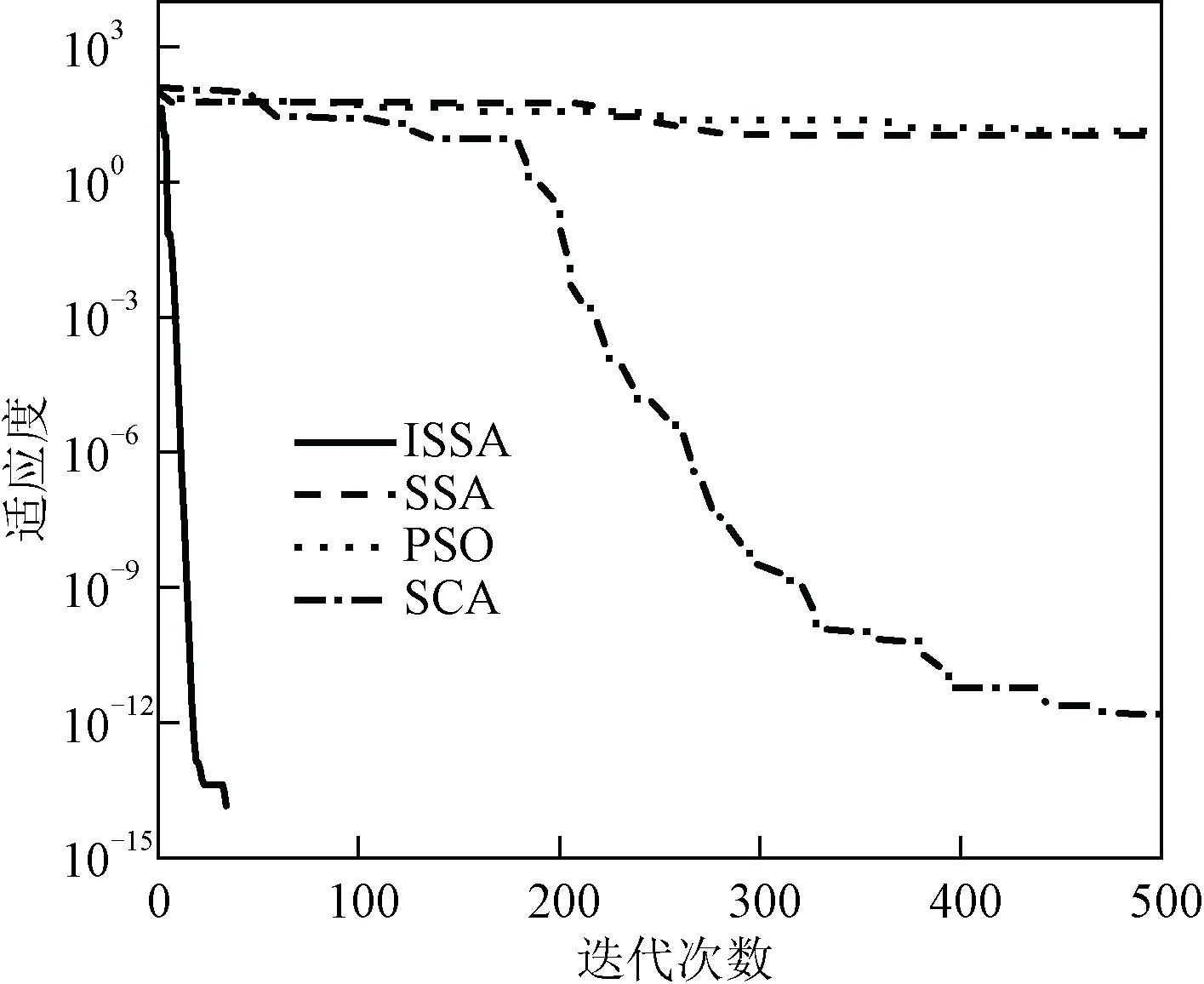
图7 f5函数寻优曲线Fig.7 f5 function seeking curve

由图3～图7可知,f1和f2函数测试中,PSO和SSA的收敛速度明显较慢,而且适应度值低,而ISSA和SCA的收敛速度更快,适应度值更高,在f3函数测试中,ISSA的收敛速度快且适应度值高,均优于其他三种算法,在f4和f5函数测试中,ISSA算法最终都趋近于最优适应度值0,而PSO、SSA和SCA适应度值相对较低,收敛速度也相对较慢。

通过以上比较实验可以证明:加入半数均匀初始化和反向学习策略以及引入非线性递减权重因子的樽海鞘群算法的寻优能力和收敛速度都得到了明显的提高,而且和其他通用算法相比,对于不同测试函数,改进后的樽海鞘群算法都具有较强的适应能力且不易陷入局部最优。

4 改进SSA算法优化的LSSVM诊断模型

4.1 LSSVM分类器

LSSVM[22]通过使用二次规划方法,将不等式约束在传统SVM中转化为等式约束,简化拉格朗日乘子α的求解,简化计算,提高收敛速度,并且在非线性系统中效果会更好。

对于变压器故障数据训练样本集T={(x1,y1),…,(xi,yi),…,(xN,yN)}∈(X,Y)N,其中xi∈X=Rn为输入,yi∈Y=R为输出,给定一个非线性映射函数φ(x),构造支持向量机的变压器故障预测模型如式(17)所示:

f(x)=ωTφ(x)+b

(17)

式中,ω为权向量;b为偏置量。

目标函数minJ(ω,e)为:

(18)

式中,e为训练集预测误差;ek为每一个样本的误差;γ为惩罚系数,其值大于0。

需要满足的等式约束为:

yk=ωTφ(xk)+b+ekk=1,2,…,N

(19)

将拉格朗日乘子α=[α1α2…αN]≥0引入,可得拉格朗日函数:

L(ω,e,α,b)=J(ω,e)-

(20)

当拉格朗日函数L取得极值时,应满足关系:

(21)

式(21)可写成如下的线性方程组:

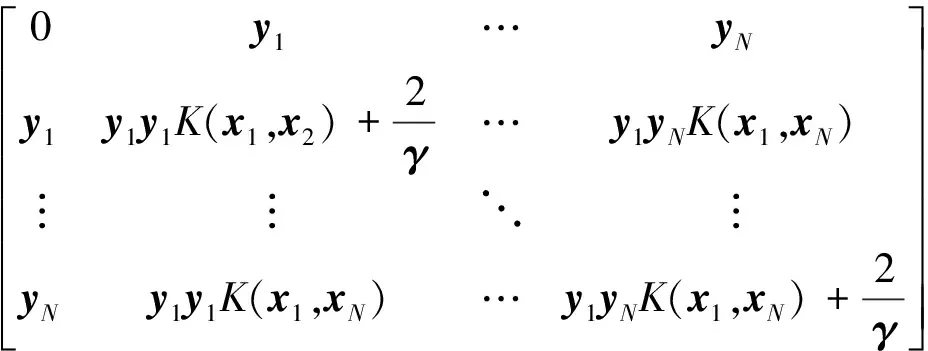
(22)

式中,K(·)为核函数,根据Mercer定理,核函数满足:

K(xi,xj)=φ(xi)T·φ(xj)

(23)

利用最小二乘法求解,可得LSSVM优化函数:

(24)

由于高斯径向基核函数有泛化能力强、可导性、对称性和光滑性佳的优点,因此本文采用高斯径向基核函数(Radial Basis Function,RBF),其表达式为:

(25)

式中,σ为核函数参数。

对于RBF核函数的LSSVM变压器故障模型,需寻优的参数为惩罚参数γ和核函数参数σ。

4.2 基于改进SSA优化的LSSVM

为提高LSSVM的变压器故障诊断精度性能,结合ISSA对LSSVM的参数γ、σ进行优化,建立ISSA-LSSVM的变压器故障诊断模型,以提高诊断精度。利用改进樽海鞘群算法优化LSSVM的γ和σ过程如图8所示。

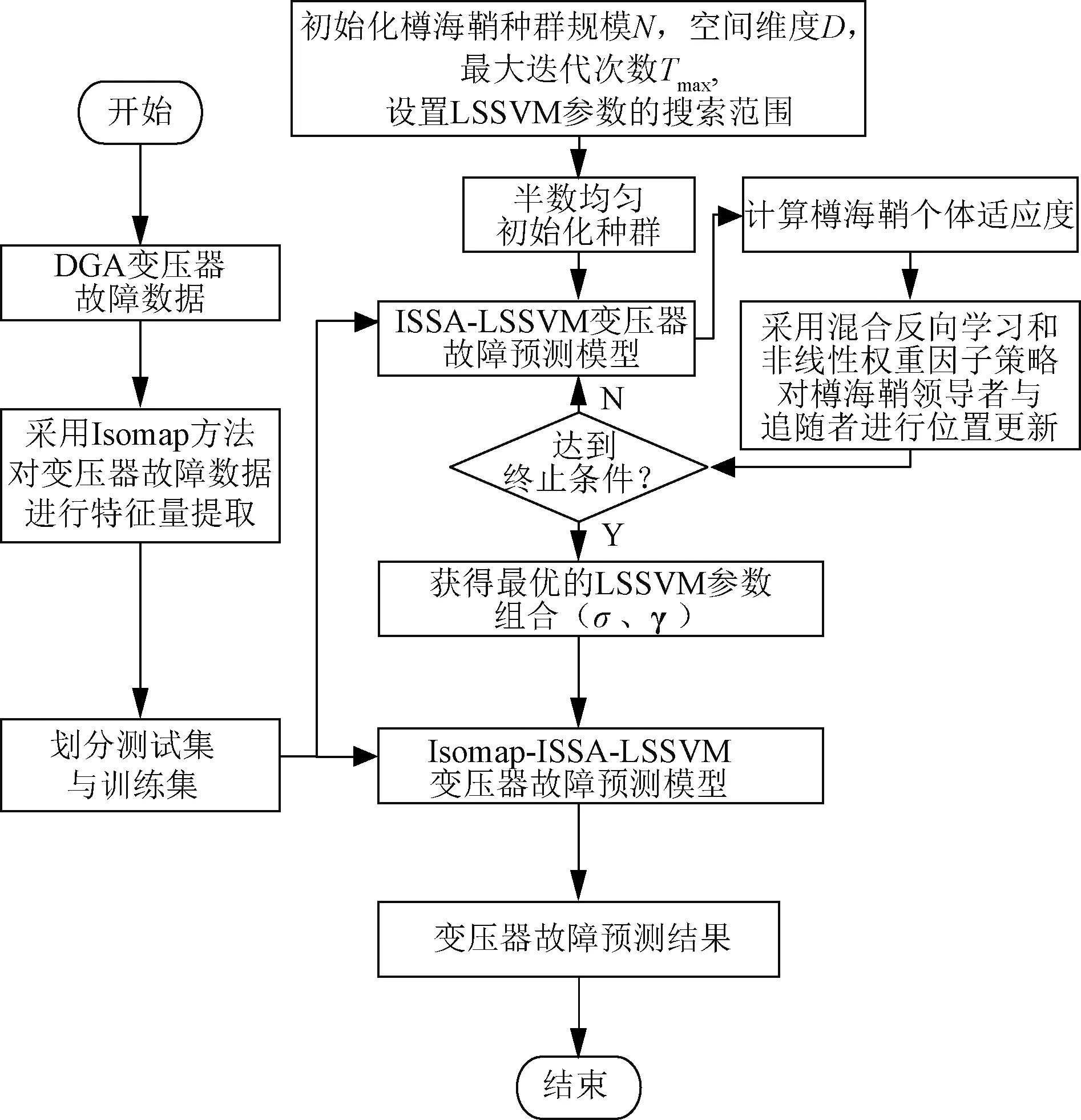
图8 ISSA优化LSSVM流程图Fig.8 ISSA optimized LSSVM flow chart

步骤1: 设定樽海鞘种群的大小为N,搜索空间的维度为D,最大迭代次数为Tmax,用半数均匀初始化方法与原始SSA算法初始化方法共同生成樽海鞘群初始位置,设置LSSVM的参数σ、γ的搜索范围为[0.01,100]和[0,200]。

步骤2: 将DGA方法构建的变压器故障数据利用Isomap方法进行特征量提取,将提取的数据按2∶1的比例分配到训练集与测试集中。

步骤3: 构建基于DGA的ISSA优化LSSVM变压器故障预测模型,计算变压器故障判别准确率并定义为樽海鞘个体的适应度函数,变压器故障模型的准确率等于正确分类的样本数与总样本数的比值。

步骤4: 根据式(13)、式(14)混合反向学习策略更新樽海鞘领导者个体位置,根据式(15)、式(16)非线性权重策略更新樽海鞘追随者个体位置。

步骤5: 通过计算新樽海鞘个体的适应度值并判断其是否符合条件,若符合条件,则将最佳参数值给予LSSVM模型,否则返回步骤3。

步骤6: 根据经过ISSA优化后的最优参数,构建了基于DGA的ISSA优化LSSVM模型,用于变压器故障分类预测,并输出相应的故障类型。

综上,通过使用ISSA来寻优LSSVM的参数,得到最优参数组合(σ,γ),输入故障诊断模型,使故障诊断的正确率得到提高。

5 方法有效性验证

本文数据由东北某供电公司提供,变压器故障诊断中,大多数研究选用绝缘油中气体成分H2、CH4、C2H6、C2H4、C2H25种故障相关气体含量值,然而,由于变压器故障类型的多样性以及故障特征之间的相互关联,如果仅仅根据气体自身成分含量进行诊断,将会对分类能力产生影响[23]。因此本文利用无编码比值法构造9种特征参量并结合绝缘油中溶解气体成分的5种故障特征相关气体,共14个特征参量组合形成变压器故障原始数据集。其中无编码比值法构造9种特征参量分别为:(CH4+C2H4)/TH、C2H4/TH、C2H4/C2H6、CH4/H2、C2H2/C2H4、C2H2/TH、C2H6/TH、CH4/TH、H2/(H2+TH),其中TH为总烃,若比值分母为0,则将分母修改为10-8以避免出现无效值。变压器原始故障数据见表4。

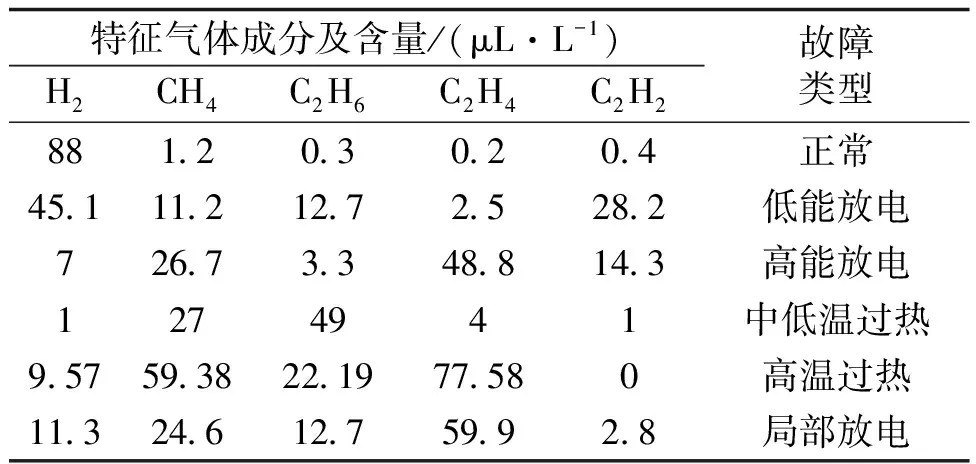
表4 变压器原始故障数据Tab.4 Original transformer fault data

5.1 数据样本处理

为保证模型的普适性和泛化能力,并针对人为挑选故障数据的主观性,从获取的500组6种运行状态的变压器原始故障数据中随机抽取360组油中特征气体数据按2∶1的比例进行训练和测试,表5中展示了测试样本和训练样本数据的分布情况。因原始数据量级相差较大,会增加模型计算复杂度,因此进行归一化处理。原始数据中故障类型分别为:正常、低能放电、高能放电、中低温过热、高温过热、局部放电,编号为1～6。

表5 实验数据集的划分Tab.5 Division of experimental data set

采用Isomap方法对变压器故障原始数据进行特征提取时,需确定的两个参数近邻点数k和低维空间维数d可通过文献调研和实验测试的方式来确定。经文献[24]调研,本文采用剩余方差来确定k和d,剩余方差越小,得到的故障特征集更能反映原始变压器数据的特征信息。对于k,剩余方差的最小值近于0.01即可,经过实验测试k=10时剩余方差满足最佳要求。剩余方差与特征数据维度的关系如图9所示。

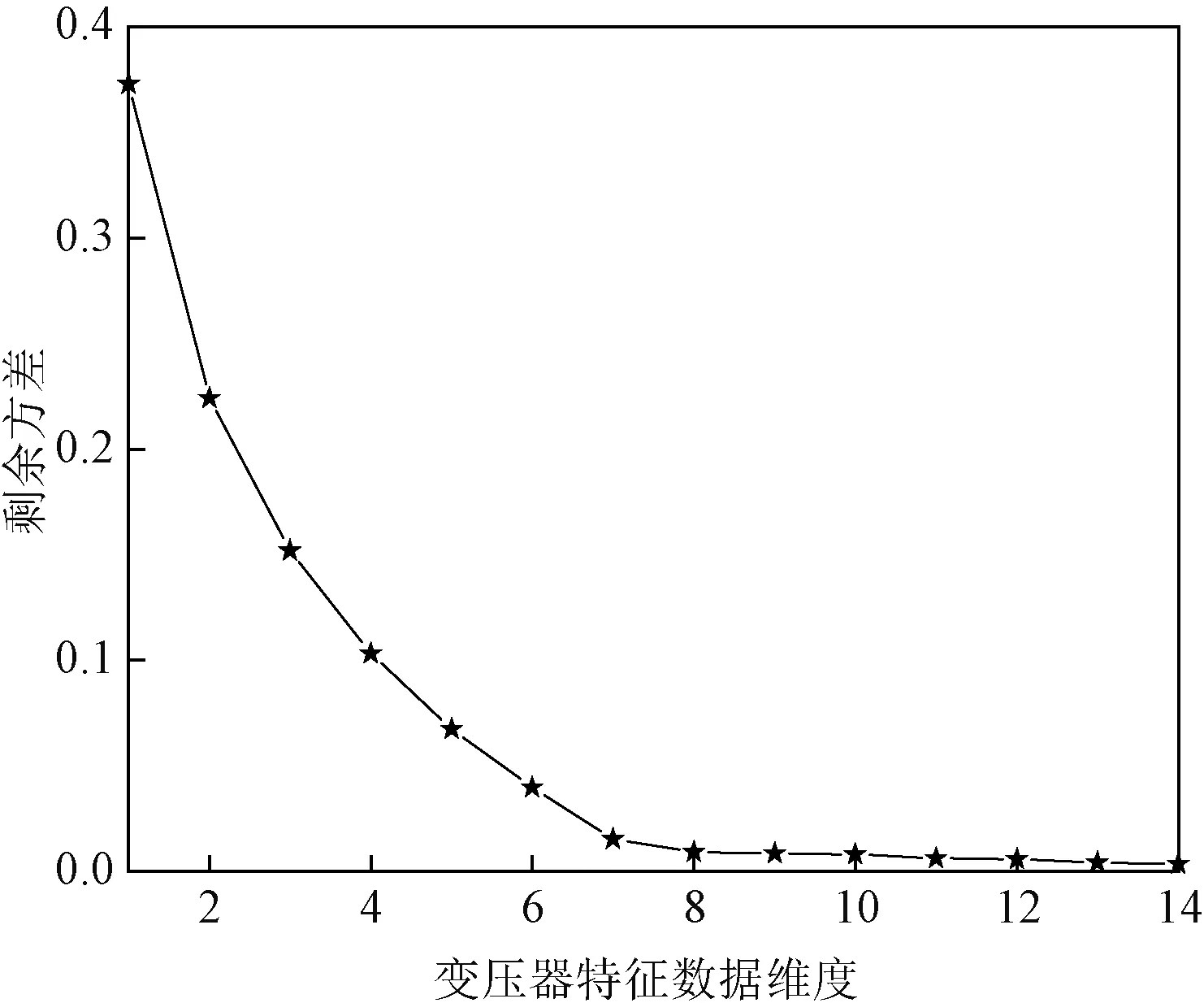
图9 剩余方差与特征数据维度曲线图Fig.9 Residual variance vs. dimensionality of feature data curve

由图9可知,剩余方差随着特征数据维度的增加而降低,当维数d增加到8以后,此时剩余方差为0.009 2保持在0.01附近,随着维度的增加,剩余方差总体呈现先减小后平稳的趋势,这时波动也趋于平稳状态,由此确定d取值为8。

为验证Isomap算法对油中溶解气体数据进行特征提取的可行性与有效性,现将Isomap算法特征提取前后的特征参量样本集输入到传统的LSSVM模型中,在相同条件下进行实验,对比特征提取前后的运行时间与诊断精度,所得结果见表6。由表6可以得出,Isomap算法更能挖掘嵌入于原始高维特征空间中的低维流形特征,以表征电力变压器的故障状态,在模型的诊断精度和运行时间上都得到了显著性的提升。

表6 Isomap特征提取前后对比Tab.6 Comparison of Isomap features before and after extraction

以Isomap算法特征提取后的特征参量样本集作为PNN、KNN、ELM、SVM及LSSVM 5种不同变压器故障诊断模型的输入,进行变压器故障诊断,对比分析其他4种模型与LSSVM变压器故障诊断模型的诊断结果,以30次实验结果作为依据,得到各个模型的最高、最低、平均正确率及标准差,结果见表7。

表7 不同模型重复训练结果Tab.7 Repeated training results for different models

由表7可知,以Isomap算法特征提取后的数据作为输入,以30次实验结果进行分析,结果表明LSSVM模型平均正确率为0.788 3且标准差为0.015 2。与其他诊断模型相比可知,基于LSSVM的变压器故障诊断模型有着较高的平均故障准确率,且30次实验结果的标准差最小、稳定性最强。

5.2 算法寻优比较

由于惩罚因子和核参数对LSSVM模型的诊断结果有重要影响,因此,优化LSSVM参数采用了ISSA算法,并与SSA、PSO和SCA算法的优化结果进行对比分析。图10展示了以Isomap特征提取后数据为输入的变压器故障诊断模型迭代曲线,其中适应度值为故障准确率。

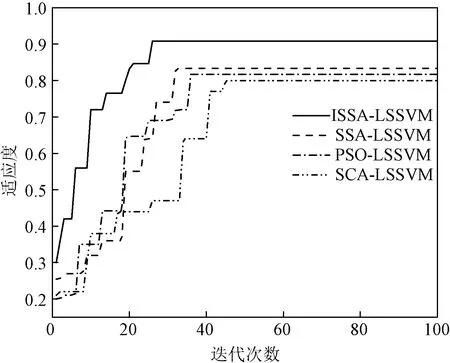
图10 适应度变化曲线Fig.10 Adaptation change curve

从图10可以看出,SCA算法的收敛速度最慢且适应度值最低,需要迭代45次才能达到收敛状态;相比之下,PSO算法在诊断精度和收敛速度上有所提升,仅需36次迭代就能达到收敛状态,准确率为0.816 7;原始的SSA算法由于其出色的优化能力,在32次迭代后就达到了收敛状态,且适应度值高于PSO和SCA算法;而改进后的ISSA算法,采用了半数均匀初始化、非线性递减权重因子和混合反向学习策略,仅需26次迭代就能达到收敛状态,且适应度值最高,为0.908 3。这验证了在有变压器故障数据介入的情况下,改进后的ISSA算法仍然能够保持较好的收敛速度和较高的诊断精度。

5.3 不同故障诊断模型对比分析

以Isomap提取后的特征信息作为ISSA-LSSVM模型的输入进行网络训练,以测试集得到分类结果。同时将诊断结果与SSA、PSO和SCA优化LSSVM进行对比,分类精度见表8,诊断结果如图11～图14所示。

表8 变压器故障诊断结果Tab.8 Transformer fault diagnosis results

图11 PSO-LSSVM故障诊断结果Fig.11 PSO-LSSVM fault diagnosis results

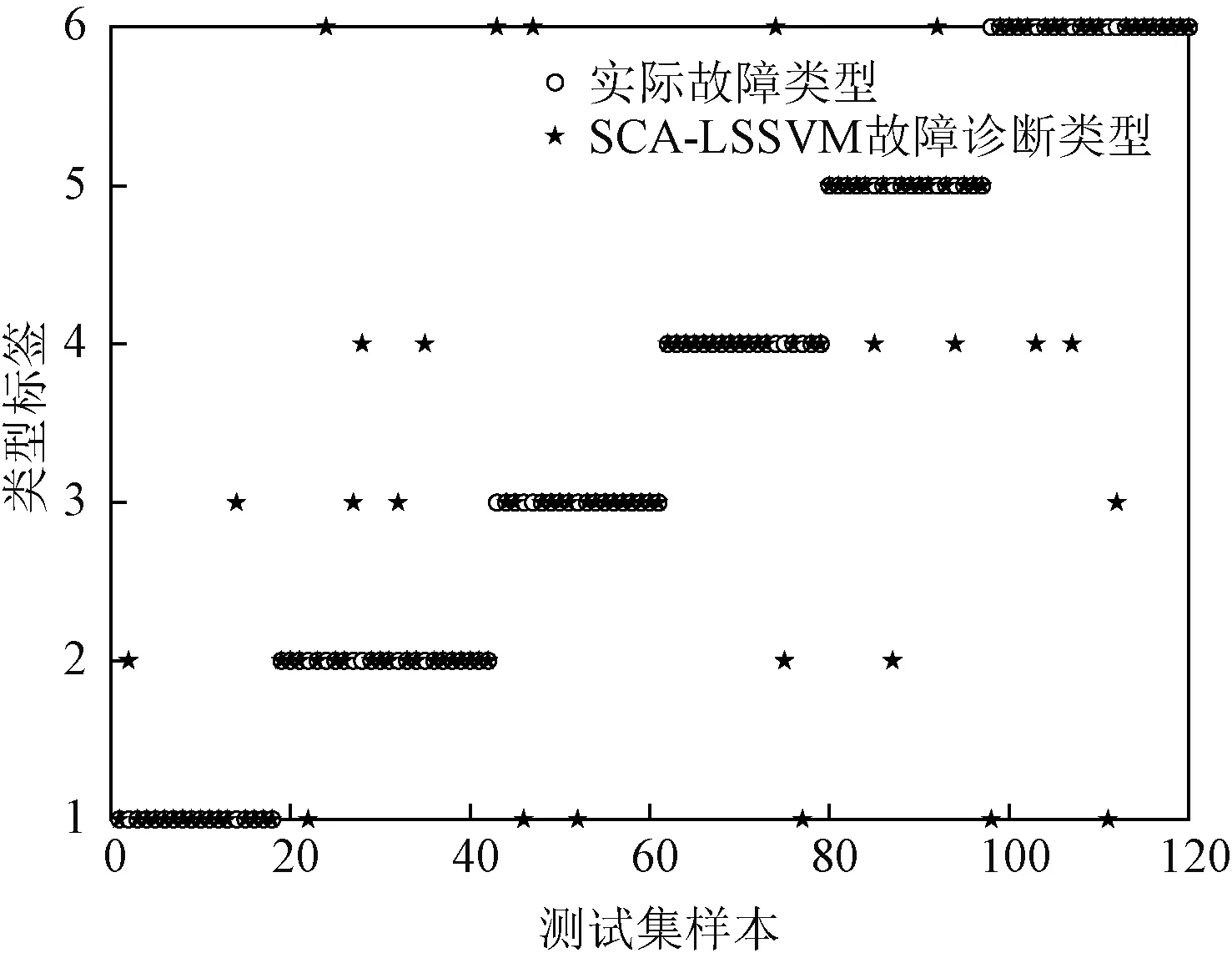
图12 SCA-LSSVM故障诊断结果Fig.12 SCA-LSSVM fault diagnosis results

图13 SSA-LSSVM故障诊断结果Fig.13 SSA-LSSVM fault diagnosis results

图14 ISSA-LSSVM故障诊断结果Fig.14 ISSA-LSSVM fault diagnosis results

由表8和图11～图14可知,以Isomap算法特征提取后的数据作为模型输入,采用ISSA-LSSVM模型进行变压器故障诊断,结果表明,ISSA-LSSVM模型对正常、低能放电和局部放电识别较好,故障诊断精度最高,达到90.83%。PSO-LSSVM、SCA-LSSVM以及SSA-LSSVM变压器故障诊断精度分别为81.67%、80%及83.33%。综上可知,经过Isomap算法对油中气体特征提取后,能够去除冗余数据对模型的影响;结合半数均匀初始化、非线性递减权重因子以及混合反向学习策略的多策略改进樽海鞘群算法对LSSVM的相关参数进行寻优,建立的综合故障诊断模型的诊断性能最优,呈现了更高的可靠性。

6 结论

(1)对于变压器复杂多样的高维原始故障数据,采用等规度映射对特征量进行提取,去除了冗余数据对模型的影响,提高了诊断精度,并且加快了收敛速度。

(2)通过半数均匀初始化、非线性递减权重因子及混合反向学习策略等改进的樽海鞘群搜索算法,丰富了种群多样性,同时提升了全局寻优性能,改善了易陷入局部最优的缺陷。

(3)仿真实验结果表明,LSSVM基准模型具有较高的变压器故障类型的判别能力,ISSA-LSSVM较PSO-LSSVM、SCA-LSSVM及SSA-LSSVM诊断方法分别提升了9.156%、7.5%和10.833%。因此,所提方法可以更加可靠、准确地诊断变压器的故障信息,具有一定的理论研究价值。