基于支持向量回归代理模型的STATCOM协同规划方法
沈玉明, 吴晓鸣, 冯沛儒, 凌 孺, 许晓龙, 罗永捷, 池 源
(1. 国网安徽省电力有限公司经济技术研究院, 安徽 合肥 230000; 2. 重庆大学电气工程学院, 重庆 400044)
1 引言
近年来,为构建高比例新能源的新型电力系统,风电开始大规模接入电力系统。然而风机的无功支撑能力相较于传统的同步发电机较弱,当在风电场近区发生短路故障的时候,电压降低致使风机的保护装置动作,风机会吸收无功致使电压进一步降低[1],在故障清除之后,系统中的感应电机负荷在恢复过程中也会吸收大量的无功功率[2],从而造成大量的无功功率缺额。为了弥补无功缺额,一般会在风电场近区配置大量的无功补偿设备,例如静止无功补偿器[3](Static Var Compensator,SVC)等。但是,在应用SVC时为了防止SVC自发振荡,往往会给SVC设置一个人为的延时,这就导致SVC在进行无功功率补偿时无法有效跟踪无功功率的缺额,容易出现因为滞后跟踪无功功率而导致在电压恢复过程中发出大量无功,使系统出现因为无功盈余而导致的过电压现象,影响到系统的电压稳定性,严重时会造成风电场大规模连锁脱机[4-7]。
静止同步补偿器(STATic synchronous COMpensator,STATCOM)作为动态无功补偿装置,可以有效改善短期电压的稳定性[8-12]。但是STATCOM发挥的作用与其安装的位置有着很大关系[12-15]。此外,作为动态无功补偿装置,其成本相较于静止无功补偿装置更高,考虑到经济性的问题,需要在容量上进行合理的优化配置,使得其在提高系统电压稳定性的同时能够尽量减少所需费用。文献[16]提出了三个优化指标来综合评估静态和短期电压稳定性,弥补了以往将静态和短期电压稳定性分开研究的缺陷。但没有考虑到风电出力的不确定性,文献[17]将风电出力的不确定性考虑在优化计算之内,同时通过利用田口正交测试数列以风电出力的上下界构成小数据集逼近庞大的风电不确定出力数据集,减少了计算量,并且也提出了三个指标,配合时域仿真以实现对系统动态无功补偿装置的容量优化配置。但是文献[17]中关于短期电压稳定性指标没有考虑到电压幅值持续越限时间,且时域仿真耗费的时间较长。
因此,本文基于已有文献,提出考虑电压幅值持续越限的改进型短期电压稳定性指标,综合考虑成本、静态电压稳定性和短期电压稳定性,以支持向量回归(Support Vector Regression,SVR)代理模型[18]代替时域仿真,结合非支配遗传排序算法实现了对含风电电力系统的动态无功补偿的容量优化配置,提高了其电压稳定性,并且在保证所需精度的前提下大幅度缩短优化计算时间。
2 基于惩罚机制的改进指标
瞬态电压严重性指数(Transient Voltage Severity Index,TVSI)[16]的计算如下所示:
(1)
式中,Tc、Tend分别为故障切除时刻和计算结束时刻;Nb为节点的数量;pk为事故k的发生概率;Vi,t,k和Vi,0,k分别为事故k后节点i在t时刻和事故k前的静态电压幅值;δ为电压越限阈值;K、B为事故总集和节点总集;瞬态电压偏移指数(Transient Voltage Deviation Index,TVDI)是基于扰动切除后的动态电压轨迹定义的,用于描述扰动切除后电压的恢复速度。
为了实现对发生故障之后电压幅值持续越限时间的优化,本文引入惩罚机制,即每当电压幅值越过规定的上限或者下限,从越限时刻开始计时,在电压幅值越限时间到达规定的时长之前,仍然按照式(1)计算TVDI,而越限时间冲过规定的时长之后,此后计算TVDI时按照式(2)计算。如图1所示,L1~L2为电压幅值低于设定范围下界的部分,L3~L4为电压幅值高于设定范围上界的部分,其中L2和L4因越限时间持续时间较长,故引入惩罚机制对其进行惩罚。
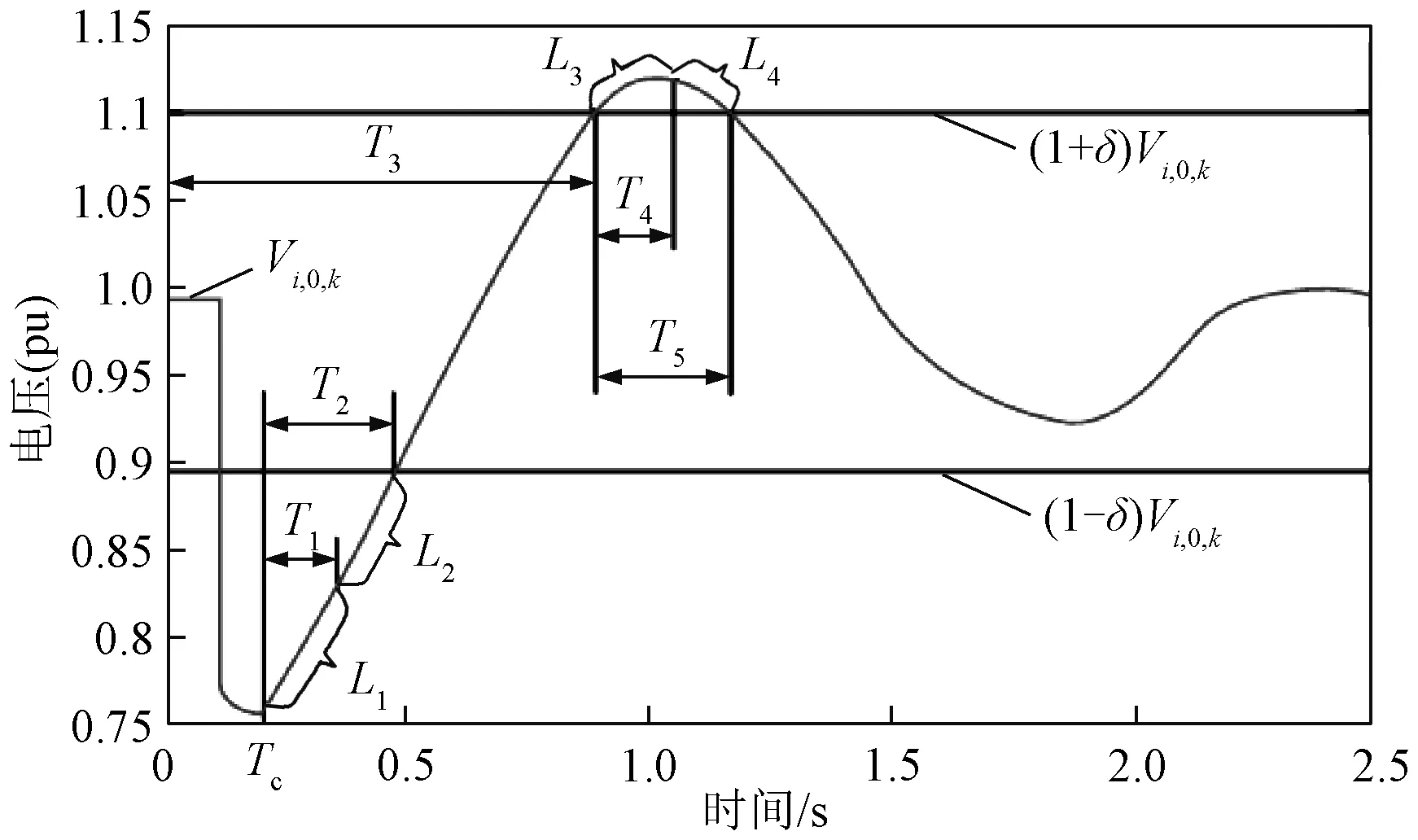
图1 引入惩罚机制的TVDI计算示意图Fig.1 Improved TVDI with penalty strategy
(2)
式中,α为介于0~1之间的惩罚系数。将式(2)中带有惩罚系数的项看作一个新的电压V′i,t,k,其计算方式则变得和式(1)一样。
3 多阶段协同规划模型
多阶段协同规划是指无功补偿装置配置、事故前和事故后阶段,实现包括成本、静态电压稳定性和短期电压稳定性的多目标优化。
(1)成本。成本作为本文多目标优化的目标之一,由STATCOM的投资费用、由于STATCOM促使的发电再调度所减少的发电成本以及为了加强应对恶劣天气而短时弃风所需要的成本。其计算为:
(3)

(2)电压崩溃接近指数(Voltage Collapse Proximity Indicator,VCPI)。该指标对于规划问题的优点包括:对任何拓扑和负载量都具有灵活性,效率高,并不需要详细的负载增量信息。其计算为:
(4)
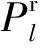
因此多目标优化模型可以建模为:
(5)
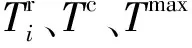
需要注意的是,风电输出具有随机性和不确定性。虽然风速通常服从威布尔分布,但风电输出是风速的非线性函数[19]。因此,风电输出的概率密度函数比威布尔函数更复杂,而对于长期规划问题,更加难以获得准确的概率密度函数。但是可以通过田口正交测试数列用一组小的具有代表性的场景在一定假设条件下逼近不确定性空间[17]。STATCOM安装位置则由VCPI和TVSI对STATCOM安装位置的灵敏度从大到小排列选定。
文献[16]提出了一种用于模拟事故选择的风险指标。
(6)
式中,M为考虑的事故总数。通过对风险指标从大到小的排序可以选择出最坏的场景,以检验所提方法在最坏情况下的适用性。
4 协同规划模型的求解
4.1 SVR代理模型
由于时域仿真需要消耗大量的时间,当考虑网络结构变化和运行阶段不确定性后,仿真时间将急剧增大。所以本文提出一种基于SVR的代理模型来缩短计算时间[18],使其在工程实际中计算成本能够被接受。以单一变量的SVR为例介绍其原理。例如现有n个训练样本{(x1,y1),…,(xn,yn)}需要进行回归,采用如式(7)所示的回归模型进行回归。
(7)

(8)

(9)
常数C是用来平衡回归函数的平坦程度与偏差大于ε的样本个数。通过拉格朗日乘子法可以得到式(9)的对偶规划问题如下所示:
(10)
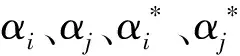
由式(10)可以得到SVR的线性拟合函数为:
(11)
对于一些不能线性拟合的情况,需要将训练数据映射到更高维度特征空间之后再进行线性拟合,根据泛函理论,映射到高维特征空间的内积运算等价于原低维空间的一个核函数K(x,x′)代换,因此,得到SVR非线性拟合函数如下所示:
(12)
不同核函数对SVR回归性能有较大的影响,选取需要一定先验知识,目前还没有一般性的结论。
由于整个优化过程只有时域仿真比较耗费时间,对应的指标是TVSI,为了在提高运算速度的同时尽量保证精度,所以SVR代理模型只是用于对TVSI进行回归,其余两个指标通过潮流计算得到。其训练流程如图2所示。首先获取训练数据,然后利用训练数据在不同的核函数条件下训练,对比精度之后选择回归效果最好的核函数作为最终核函数来建立回归模型。

图2 SVR代理模型训练流程Fig.2 Training process of SVR surrogate model
4.2 非支配排序遗传算法
将训练好的SVR代理模型结合非支配排序遗传算法来实现对成本、静态和短期电压稳定进行多目标优化,最终可以得到一系列可行解构成的帕累托前沿,可供使用者按照自己的偏重选择对应的解。图3为计算流程图。
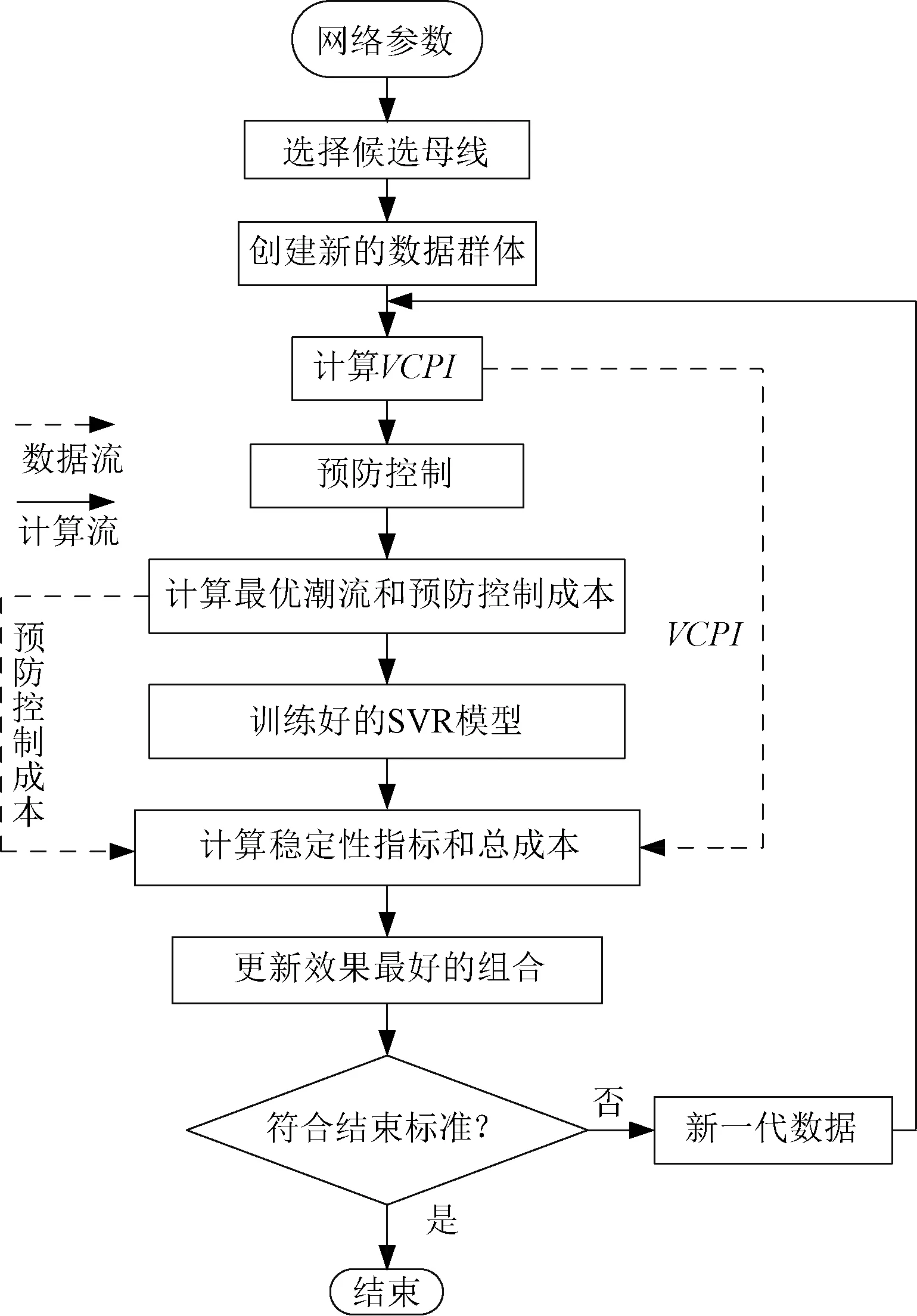
图3 计算流程图Fig.3 Computation flowchart
首先搭建用于测试的模型,在设置好各种参数之后,由非支配排序遗传算法生成初始STATCOM的安装容量和短时弃风比例,然后进行潮流计算以得到VCPI;将STATCOM的安装容量和短时弃风比例代入已经训练好的SVR代理模型之中得到TVSI;对比每种配置方案计算得到的指标,选择这一代效果最好的几个配置方案保留,然后再将容量数据和弃风比例进行交叉、重组得到新的数据种群继续重复计算成本、VCPI和TVSI,对比大小、保留和更新数据[20],直到满足结束条件之后,最终得到一个由多种配置方案构成的帕累托前沿。
5 算例分析
采用新英格兰10机39节点及与文献[16]中相同的动态元件模型进行时域仿真,得到的训练数据对SVR代理模型进行训练。SVR代理模型的核函数库包括:Matern5/2、Matern3/2、Polynomial、Sigmoid、Exponential、Gaussian,其表达式如式(13)~式(18)所示:
(13)
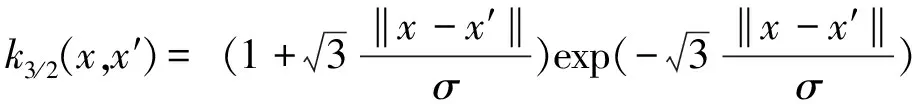
(14)
kpoly(x,x′)=(xTx′+d)pd≥0p∈N*
(15)
(16)
(17)
(18)
对比各核函数之后,最终选择精度最高的核函数为Matern5/2,经过训练之后得到的SVR代理模型在保证精度的前提下大幅度地提高了优化计算速度。图4展示了训练样本SVR的回归结果和实际结果之间的对比,同时展示了回归误差。所有误差均在0.6%以内,其中98.84%的训练样本的误差控制在0.5%之内,训练精度较高。

图4 训练样本结果Fig.4 Results of training samples
图5展示了采用时域仿真和SVR代理模型结合非支配排序遗传算法计算得到的帕累托前沿的对比,遗传算法每代的数据种群数量为100个。

图5 SVR代理模型预测结果评价Fig.5 Prediction results evaluation of SVR surrogate model
图5(a)对比了SVR代理模型和时域仿真计算得到的值,图5(b)则展示了测试数据中误差和对应TVSI之间的误差关系。误差计算方法如下所示:
(19)
式中,resultSVR、resulttime分别为SVR代理模型预测结果和时域仿真结果。从图5(b)中可以看出,即便有一些数据的回归误差超过了0.5%,也都是TVSI较大数据的回归误差较大,造成这种现象是由于在选择训练样本时,主要选择在0.79~0.9之间的样本,而其他范围的样本较少,导致在其他范围的样本数量不足,所以误差较大。并且在选择方案时如果更加侧重于短期电压稳定性,则一般选择使得TVSI较小对应的方案,此时的回归误差控制在0.5%之内,满足误差要求。
选取使得TVSI最小的STATCOM容量配置和弃风比例的方案,并且考虑短时弃风和低电压甩负荷,分别采用两种方法计算其对应的成本、VCPI和TVSI,然后记录其所花费的时间。表1中,方法一中的TVSI由SVR代理模型计算得到;方法二中的TVSI直接通过时域仿真计算得到。

表1 方法对比Tab.1 Methods comparison
对比方法一和方法二,可以发现时域仿真所需
的时间为26.35 h,而采用SVR代理模型所花费的时间仅为其十分之一(0.27 h),因此采用SVR代理模型来计算该多目标优化模型可以节约大量时间。
将含有惩罚系数的部分作为一个整体,图6展示了36号节点在发生故障时的等效电压曲线,图6中阴影部分的下包络线和其余曲线组成了36号节点的电压变化轨迹。设定在0.2 s时故障清除,电压开始恢复,越限持续时间超过0.05 s开始惩罚,惩罚系数α为0.1。可以发现引入惩罚机制的电压曲线在越限时间超过规定时间的部分被人为严重化,此时按照式(1)计算TVSI,引入惩罚机制所计算出的TVSI将会更大,能够更准确反映电压幅值持续越限对系统电压稳定性的影响,利用该指标去优化STATCOM容量能够获得更好的电压稳定性提升。

图6 有惩罚机制的36节点的等效电压曲线Fig.6 Equivalent voltage curve of 36th node with penalty mechanism
6 结论
本文在提出基于SVR代理模型与非支配排序遗传算法的STATCOM容量配置方法,相比于时域仿真方式,在保证短期电压稳定性评估精度的前提下大大缩短了计算时间,有助于该优化模型在工程实际中的应用;同时在基于电压响应轨迹的短期电压稳定性指标TVSI的基础上考虑电压持续越限的时间,引入惩罚机制来反映电压持续越限对电压稳定性的影响,能够获得更为准确的电压稳定性评估结果,提高STATCOM规划成效。

