电网对称短路故障下双馈风电系统同步稳定分析及致稳控制策略
王聪博, 余 越, 黄 森, 裴金鑫, 王剑锋, 姚 骏
(1. 电网安全与节能国家重点实验室(中国电力科学研究院有限公司), 北京 100192; 2. 输配电装备及系统安全与新技术国家重点实验室(重庆大学), 重庆 400044; 3. 重庆嘉陵华光光电科技有限公司, 重庆 400700)
1 引言
由于能源危机加剧以及环境恶化,风能等可再 生能源的开发力度持续扩大[1,2]。双馈感应风力发电机(Doubly Fed Induction Generator,DFIG)因其变速恒频、效率高以及技术成熟等优势,现已成为大规模并网风电的主流机型[3,4]。然而,受限于电力电子器件的弱抗扰性,风力发电机组在电网严重对称短路故障条件下极易出现失步脱网事故[5-7]。可见,大规模风电并网给电力系统的可靠性带来巨大挑战[8]。因此,亟需对DFIG在对称短路故障下的同步稳定机理和关键致稳技术展开研究。
目前,风电系统在电网对称短路故障下的同步稳定问题已引起了工业界和学术界的广泛关注。为保障含风电电力系统的安全稳定运行,国内外系统运营商已经普遍针对风电机组制定了相应的并网导则,要求机组在短路故障下应具备低电压穿越(Low Voltage Ride Through,LVRT)能力[9,10]。文献[11]揭示了DFIG静态稳定极限,但是并未涉及电网短路故障场景下的同步稳定机理分析,并且忽略了锁相环(Phase-Locked Loop,PLL)的控制效应,未能准确刻画揭示DFIG的同步机制。文献[7]采用相平面法揭示了新能源发电系统的同步失稳机理,但该方法难以提供清晰的物理视角,不能识别出造成锁相环失步的主导因素,也无法给出一个通用的稳定判据。文献[12,13]则通过动态矢量三角形图示法,分析了风电系统各电压矢量的相对运行变化趋势,初步揭示了系统的同步失稳演化规律及其失稳形态。文献[14]指出风电并网系统在电网深度故障条件下的同步稳定裕度大幅减小,此时若有功/无功电流指令设置不当,系统工作点将越过可控范围造成系统与电网失去同步。除此之外,文献[15]指出随着电网强度的逐渐弱化,风力发电系统在故障持续期间还存在小信号失稳风险。文献[16,17]则提到不合适的锁相环参数或者内部电流环参数同样会导致DFIG出现小信号振荡问题。但是,文献[15-17]并未给出明确的小信号同步稳定判据。
与此同时,现有研究也提出了一些同步稳定控制方法。文献[18]提出了一种PLL附加阻尼控制策略,可显著抑制风力发电系统的小信号振荡,但是该策略无法应对平衡点缺失所带来的失稳风险。文献[19,20]则提出了基于线路阻感比的有功/无功电流指令最优配比方法,能够确保风电系统在故障期间一定存在平衡点,但该方法很可能无法满足电网导则的无功需求。文献[13,21]则从自稳性的角度出发,提出将PLL角频率偏差引入到有功电流/功率指令,从而实现系统平衡点的自动调节,但该策略极易受变流器容量限制。
综上所述,针对电网对称短路故障下DFIG 的同步稳定问题已有一些研究成果,但缺少定量分析方法,此外,现有的稳定控制策略应用场景受限,适应性较差。因此,亟需对DFIG在短路故障下的同步稳定机理、量化失稳判据以及可塑性较强的稳定控制方法展开研究。本文从PLL的锁相同步原理出发,揭示了DFIG系统的同步失稳机理,发现了可同时满足大/小信号同步稳定性约束的DFIG理想稳定运行区域,基于此,本文提出了一种基于虚拟负电阻的锁相环改进控制方法,可等效地抵消电网阻抗的电阻效应,进而增强LVRT期间DFIG的同步稳定性。最后,利用仿真与实验算例对理论分析的正确性和所提控制策略的有效性进行了验证。
2 LVRT期间并网DFIG同步稳定边界
2.1 DFIG等效电路模型
DFIG的结构及其控制框图如图1所示。图1中U、E分别为故障点电压矢量与DFIG并网点电压矢量;I为DFIG输出电流矢量;Z和Zg分别为DFIG出口端到故障点间的线路阻抗矢量以及故障点到无穷大电网之间的等值连接阻抗矢量;ωPLL和θPLL分别为PLL的输出角频率和输出角度;Lg和Cf分别为DFIG网侧变换器的滤波电感和并网点处的滤波电容;Udc为DFIG变换器直流母线电压。
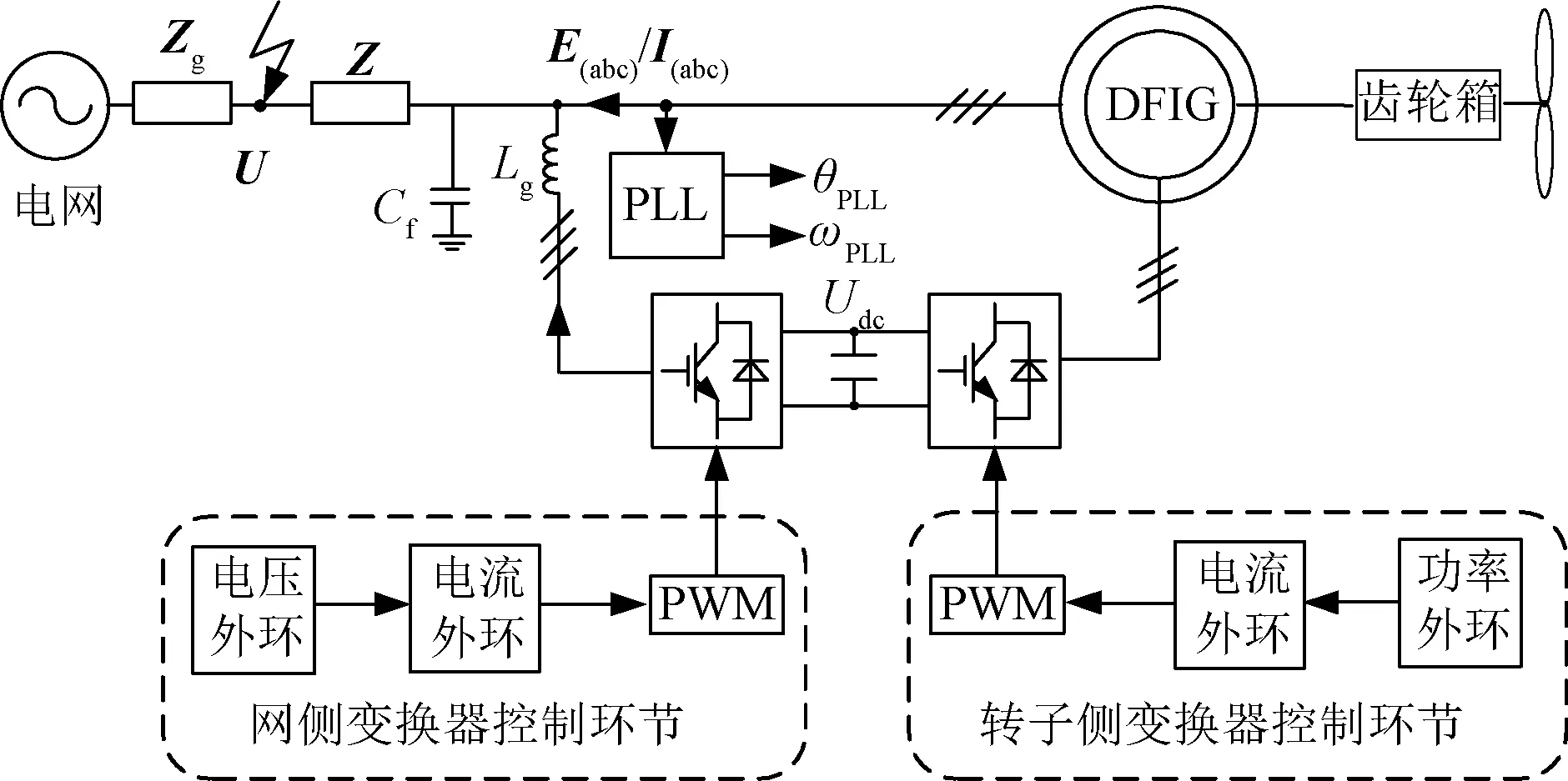
图1 DFIG控制框图Fig.1 Control diagram of DFIG
在电网正常运行工况下,为实现最大功率跟踪和单位功率因数运行,DFIG的转子侧变换器(Rotor Side Converter,RSC)采用包含功率外环以及电流内环的双环工作模式。当检测到电网发生三相对称短路故障后,RSC将立刻闭锁功率外环,直接采用单电流环控制模式,以满足电网导则的快速无功要求。此时,DFIG处于定电流工作模式,可等效为图2所示的受控电流源,φ为机端到故障点之间的相位差,θi为DFIG输出电流与机端电压之间的相角,θz为对应线路阻抗的阻抗角。
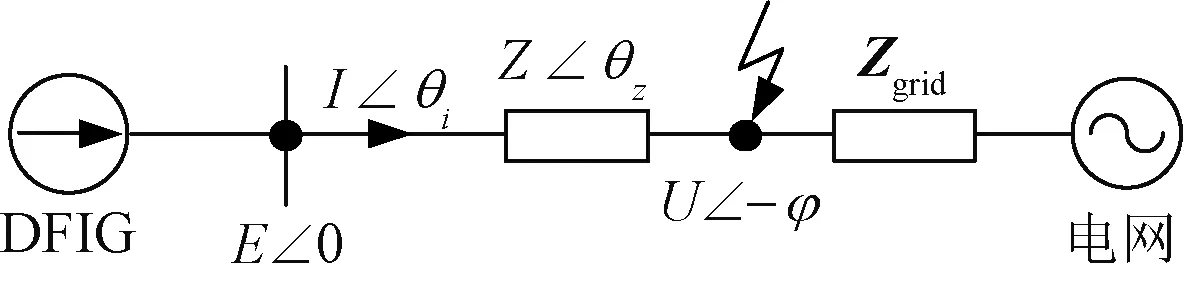
图2 电网短路故障下DFIG等效电路Fig.2 Equivalent circuit of DFIG under grid fault
PLL是DFIG实现与电网同步的关键环节。图3给出了典型的PLL控制框图。图3中,ω0为电网额定角频率,Ed和Eq分别为并网点电压在锁相环坐标系下的dq轴分量。
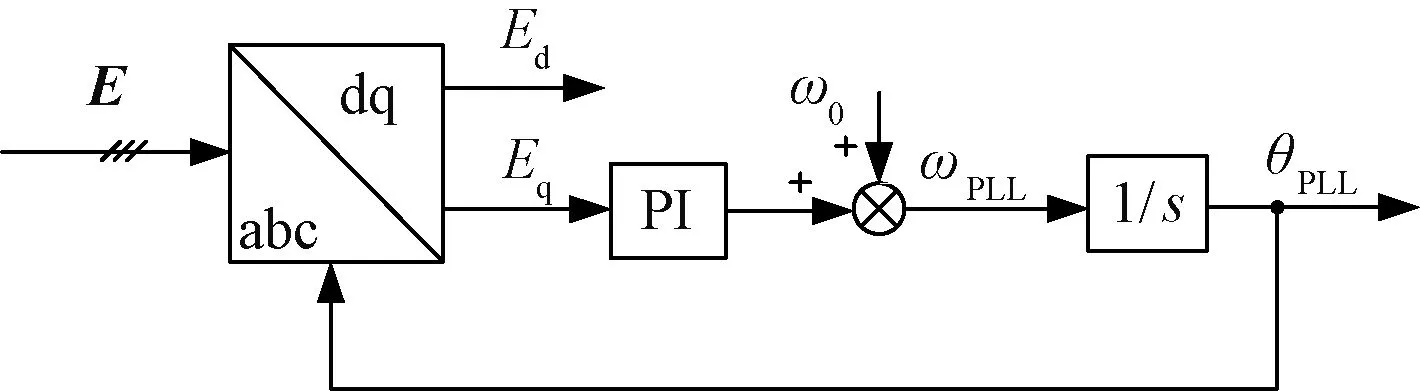
图3 PLL控制框图Fig.3 Control diagram of PLL
由于本文主要研究由锁相环主导的同步稳定性。因此,在PLL的控制带宽远低于电流环的情况下,可合理忽略电流环的动态,即DFIG的输出电流可以瞬间跟踪其参考值(I=Iref)。结合图2和基尔霍夫电压定律,可得电压矢量方程为:
(1)
由式(1)可知,端电压矢量E由电网电压U和阻抗压降IrefZ两部分电压矢量组成。
2.2 DFIG大信号同步稳定边界
根据图3,可以看到PLL的输入信号为E,并通过对Eq进行无静差消除,即可实现对电网电压的准确跟踪。在稳态时,E、IrefZ以及U之间的电压矢量关系图如图4所示,其中Eq不仅取决于U在q轴上投影,同时受IrefZ在q轴上投影的影响,这意味着DFIG与电网阻抗的交互作用将会影响PLL的输入,从而影响PLL对U的跟踪效果。根据图4,可得到Eq的表达式为:

图4 E、IrefZ以及U之间的矢量关系图Fig.4 Vector diagram between E,IrefZ and U
Eq=IrefZsin(θi+θz)-Usinφ
(2)
式中,IrefZsin(θi+θz)为IrefZ在q轴上的投影值,由于电流指令明确,该项是定值;Usinφ为U在q轴上的投影值,受三角函数约束,Usinφ最大值是U。当IrefZsin(θi+θz)和Usinφ之间关系满足式(3)时,则意味着Eq可被PLL调节至0,DFIG存在稳定工作点,系统不会因平衡点缺失而与电网失去同步。
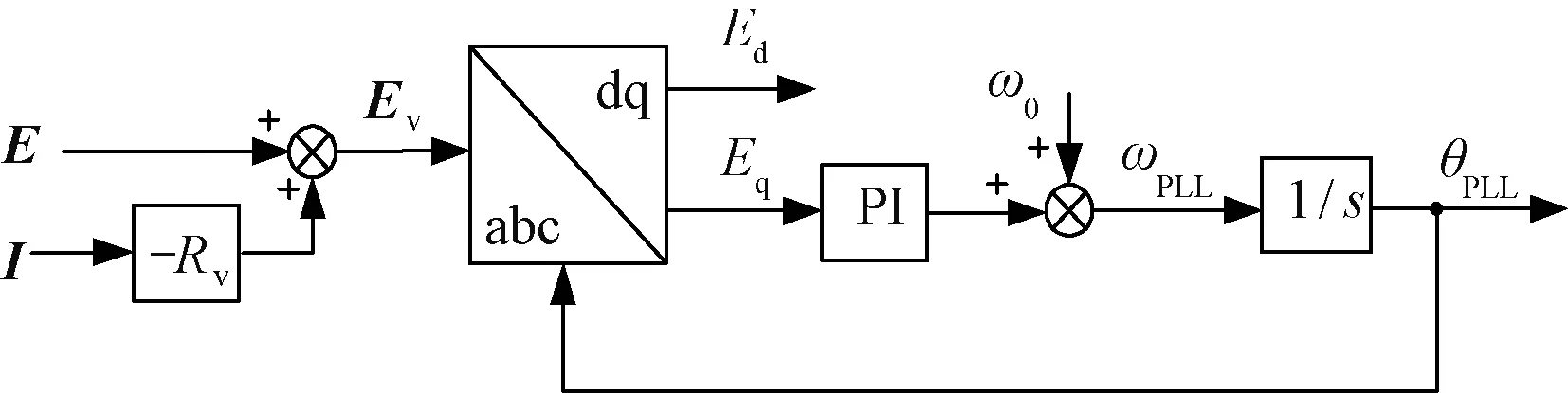
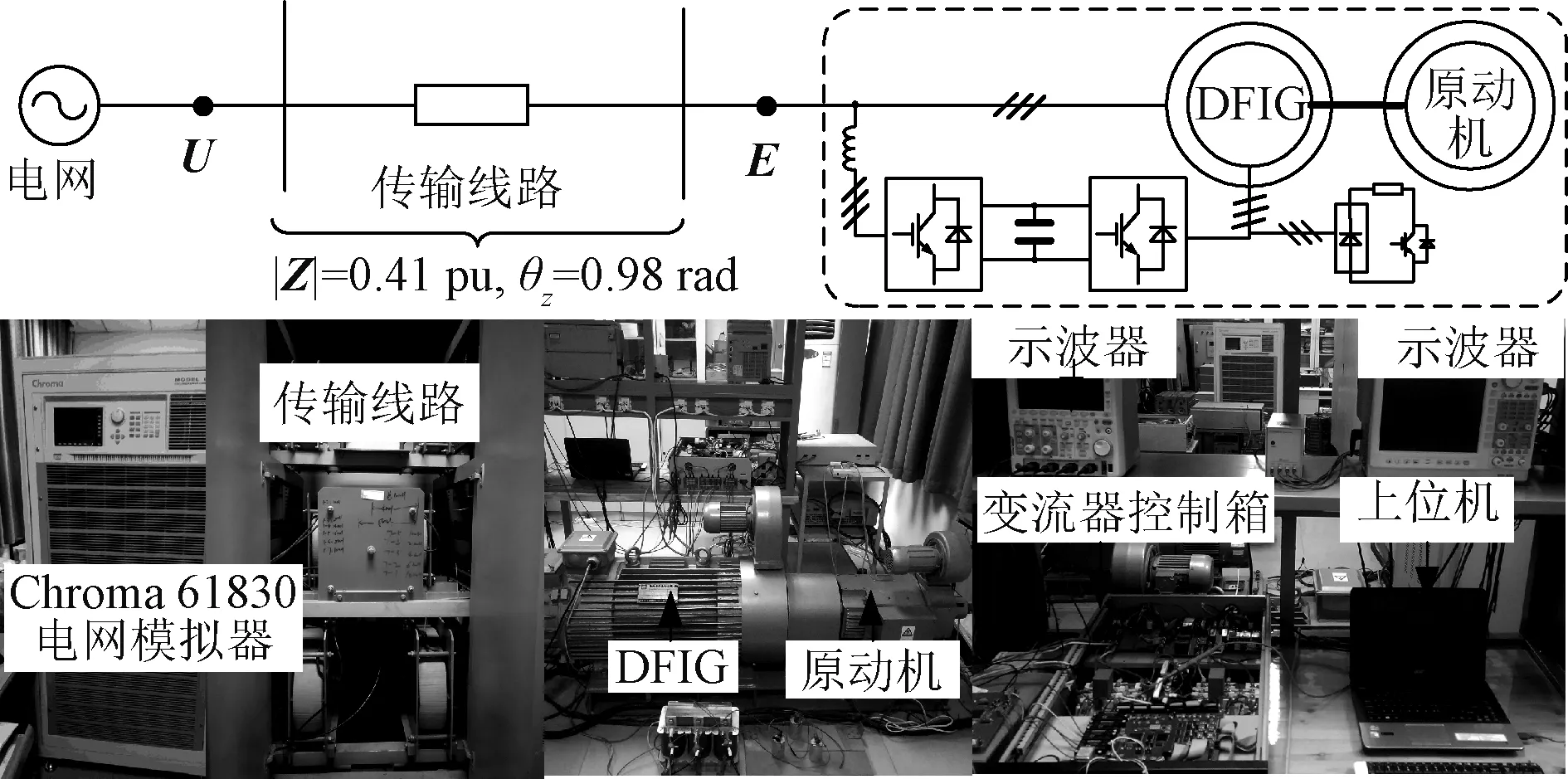
IrefZsin(θi+θz) (3) 然而,当IrefZsin(θi+θz)和Usinφ之间的关系不满足式(3)时,无论φ为何值,U在q轴上的投影永远无法抵消IrefZ在q轴上的投影,即Eq始终无法被调节至0,这将导致DFIG平衡点缺失。此时,锁相环PI控制器的输入信号将恒为正值或负值,进而造成其输出信号ΔωPLL单调增加或者减小,引起φ(φ=θPLL-θug,θug为故障点电压相角)的增加或者减小,并最终导致DFIG系统与电网失去同步。 因此,根据式(2)和式(3),可推导得到DFIG的大信号同步稳定运行边界: (4) 由式(4)可知,电网电压跌落程度越深,阻抗压降越大,DFIG大信号同步稳定运行区域越小。一旦在电流给定值下的阻抗压降与DFIG并网点电压的相角差|θi+θz|超过(|θi+θz|)1,DFIG必然将因为不存在大信号同步稳定工作点而发生失步脱网事故。 根据图3和式(2)可得: (5) 式中,kp、ki分别为锁相环PI控制器的比例、积分系数;x为选取的系统状态变量之一,等于Eq对时间的积分;ωg为电网电压角频率。 进一步,可推导出系统的小信号状态空间方程和特征方程为: (6) |sN-A|=s2+skpUcosφ+kiUcosφ=0 (7) 式中,Δx和Δφ为状态变量偏移量;A为特征矩阵;N为单位矩阵。当φ位于区间[-π/2,π/2]内时,特征根具有负实部,表明此时DFIG 具有小信号稳定性。根据式(7)可进一步推导出阻尼比ζ为: (8) 由式(8)可知,电压跌落程度(U),PLL控制参数(kp、ki)以及系统运行状态(φ)均会影响ζ。其中,不恰当的系统运行状态会使ζ减小,甚至变为负值,从而导致DFIG小信号失稳。因此,式(9)是系统小信号稳定的前提。 (9) 若将式(9)代入式(2)可得: (10) 由式(10),推导出DFIG小信号稳定边界: (11) 比较式(4)和式(11),可以看到(|θi+θz|)s与(|θi+θz|)l的解析表达式相同。也就是说DFIG的大/小信号稳定性相互耦合,系统工作点一旦越过稳定边界,系统将同时发生大信号失步和振荡频率逐渐增大的同步失稳现象。 结合2.2节与2.3节的分析结果,可以将系统工作点的运行范围划分为两个区域: 区域1:同时满足大/小信号同步稳定的同步稳定运行区域。 (12) 当|θi+θz|位于该区域内时,可同时保证系统平衡点存在和阻尼比为正。 区域2:同步失稳区域。 (13) 当|θi+θz|位于该同步失稳区域内时,DFIG不仅没有平衡点,系统阻尼比也将为负数。这时,系统将同时发生大信号失步和振荡现象,且在失稳过程中振荡频率逐渐升高。 综上,本节在考虑DFIG大/小信号同步稳定约束的基础上,通过解析法刻画了系统工作点的稳定运行区域,不仅可作为DFIG系统的同步稳定判据,还可为系统同步稳定控制策略的设计提供意见。 需要说明的是,在传统电力系统中同步发电机由于转子惯量大,使其在故障期间的转速和角度变化较为缓慢,故主要关注同步发电机在故障清除后的同步稳定性。而以锁相环为同步单元的DFIG发电系统暂态响应较为快速,并且根据电网导则要求在故障期间内即实现同步,再加之故障发生后电网电压跌落,稳定裕度骤降,导致新能源发电系统的同步失稳主要发生在故障切除前,因此DFIG发电系统的同步稳定问题则主要关注系统在故障期间的同步行为。 结合式(12)可以看到,|θi+θz|越接近于0°,DFIG的工作点距离同步稳定运行边界越远,同时也就意味着系统的同步稳定性越强。若输电线路为纯感性(即θz=π/2),则θi=-π/2时可确保|θi+θz|减小至0,从而保证故障期间DFIG系统的工作点一定位于同步稳定运行区域。虽然实际输电线路并非纯感性,但可在PLL的控制环路中引入虚拟负电阻,等效地消除输电线路的电阻分量,从而使DFIG在故障期间近似地运行在虚拟纯感性电网条件下。 基于虚拟负电阻的改进PLL控制结构如图5所示,图5中,Ev和-Rv分别为虚拟并网点电压和虚拟负电阻。 图5 基于虚拟负电阻的改进PLL控制结构示意图Fig.5 Schematic diagram of improved PLL control structure based on virtual negative resistance 采用基于虚拟负电阻策略的PLL后,DFIG的等效电路图如图6所示。其中,φv为Ev与U之间的相角差。 图6 采用虚拟负电阻PLL的DFIG系统等效电路Fig.6 Equivalent circuit of DFIG system with virtual negative resistance 根据图6可知此时DFIG的外特性表达式为: (14) 式中,θi=-π/2;θz∈[0, π/2];Zt为虚拟并网点至故障点的总阻抗,其表达式为: (15) 由图6、式(14)以及式(15)可知,等效传输线的阻抗角由θz变为θt,故Ev的q轴分量表达式为: Evq=IrefZtsin(θi+θt)-Usinφv (16) 与2.2节类似,采用虚拟负电阻控制策略后,仅在满足式(17)时,DFIG才存在平衡点。 |IrefZtsin(θi+θt)|≤U (17) 基于式(17),可以推导出Rv的范围为: (18) 结合上述分析,可以看到附加Zv的本质是改变锁相环的结构,从而改变传输线路的阻抗角,使得DFIG的工作点位于大信号同步稳定边界内。因此,当Rv满足式(18)时,可以保证DFIG不会因平衡点缺失而发生同步失稳现象。 根据式(8),可知系统阻尼比ζ与cosφ大小有关,未采用所提负电阻控制策略时,cosφ为: (19) 采用所提控制策略后,与式(5)~式(7)的推导步骤同理,系统阻尼比ζv变为: (20) 其中 (21) 由式(20)和式(21)可知,除PLL本身的控制参数外,改进锁相环后系统的阻尼比ζv还与Iref、U、R和Rv有关。其中,Rv可以等效地消除R,特别是当Rv=R时,系统阻尼比可以得到有效改善,从而提升DFIG的小信号稳定性。 此外,为了确保ζv为正,必须满足式(22)。 (22) 由式(22),对应虚拟负电阻Rv取值范围为: (23) 值得注意的是,式(23)与式(18)相等,这意味着在PLL上附加适当的虚拟负电阻,不仅可增强系统的大信号稳定性,同时还可提高小信号稳定性。因此,所提策略对DFIG故障穿越能力提升显著。值得一提的是,虚拟负电阻仅在电网短路故障条件下使能,在系统正常运行期间并不投入使用,因此不会对系统正常运行状态造成影响。 基于Matlab/Simulink仿真平台,搭建如图7所示的DFIG时域仿真模型以验证上述分析。仿真的主要参数见表1,其中,仿真参数标幺值以风机额定参数为基准值。 表1 仿真参数Tab.1 Simulation parameters 图7 DFIG仿真模型Fig.7 Simulation model for DFIG 下面将给出4个仿真算例分别对DFIG的稳定机理以及控制策略进行验证。仿真结果如图8~图11所示,在图中分别给出了各个算例下的DFIG并网点三相电压、输出电流dq轴分量、并网点电压幅值以及PLL输出角频率。 图8 算例1仿真结果Fig.8 Simulation results of case 1 图9 算例2仿真结果Fig.9 Simulation results of case 2 仿真算例3:为避免算例2中的失稳现象,现采用虚拟负电阻控制策略对DFIG的同步稳定性进行改善,其中Rv设置为0.228 5 pu (Zv=-0.228 5+j0),即等于R。如图10所示,在虚拟负电阻的作用下,DFIG顺利完成了故障穿越,并且由于PLL的阻尼比达到最大,同步过程快速平稳,系统能够迅速恢复至稳定状态。 图10 算例3仿真结果Fig.10 Simulation results of case 3 图11 算例4仿真结果Fig.11 Simulation results of case 4 为了进一步验证第2节理论分析的正确性与第3节所提控制策略的有效性,现基于含DFIG的动模实验系统进行实验研究。该系统拓扑结构及其实验参数分别如图12和表2所示,其中实验参数标幺值以风机额定参数为基准值。 表2 实验参数Tab.2 Experimental parameters 图12 实验平台Fig.12 Diagram of experimental setup 设定电网在0.2 s发生三相对称故障,电网电压降至0.2 pu, DFIG系统触发crowbar电路衰减暂态故障分量,并在0.3 s左右切断crowbar。实验算例1和算例2分别验证失稳边界的正确性和所提虚拟负电阻控制策略的有效性。实验结果如图13和图14所示,图13中的Ig、Ir和Is分别为DFIG网侧变换器输出电流、转子电流和定子电流。 图14 算例2实验结果Fig.14 Experimental results of case 2 上述仿真和实验研究对理论分析和控制策略进行了详细验证,证明了本文所提DFIG同步稳定判据的正确性以及虚拟负电阻控制策略对改善LVRT期间DFIG大/小信号同步稳定的有效性。 针对DFIG风电并网系统在电网对称短路故障下的同步稳定问题,本文在考虑锁相环同步机制的基础上,通过解析法推导了系统的稳定运行边界。在此基础上,进一步将DFIG系统的同步稳定运行区域准确地划分为同步稳定运行区和同步失稳区两个部分,从而完善了DFIG系统的同步失稳判据。最后,为增强系统的故障穿越能力,本文提出了一种虚拟负电阻控制策略,该策略可以等效地消除传输线路的电阻效应,既能有效地增强系统的大信号同步稳定性,又能提高阻尼比,改善系统的小信号稳定性,具有良好的控制效果。值得一提的是,本文的分析结果和控制方法也可以扩展到其他锁相同步型新能源发电系统,例如永磁直驱风力发电机系统和光伏发电系统。2.3 DFIG小信号同步稳定边界
2.4 DFIG的稳定运行区域
3 同步稳定控制策略
3.1 虚拟负电阻控制策略
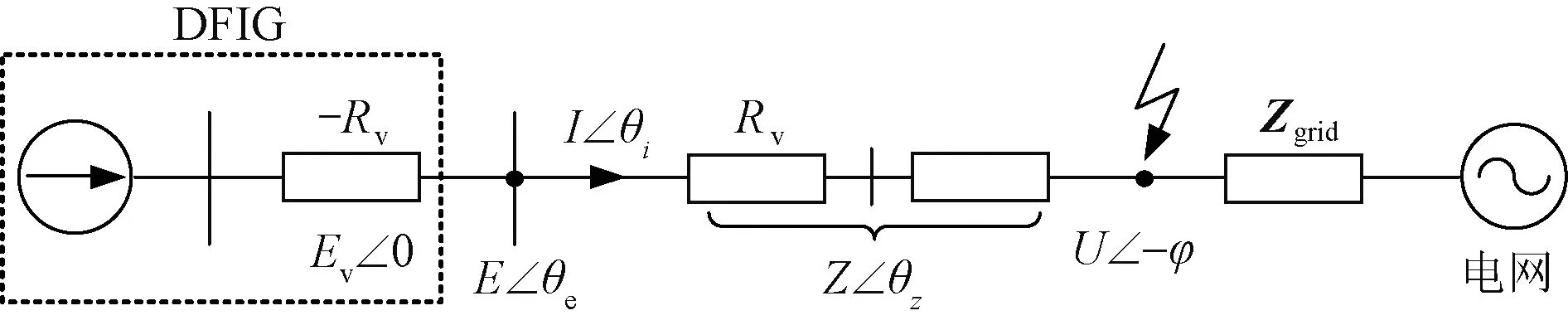
3.2 采用虚拟负电阻控制策略后DFIG的大信号同步稳定性
3.3 采用虚拟负电阻控制策略后DFIG的小信号同步稳定性
4 仿真与实验研究
4.1 仿真研究

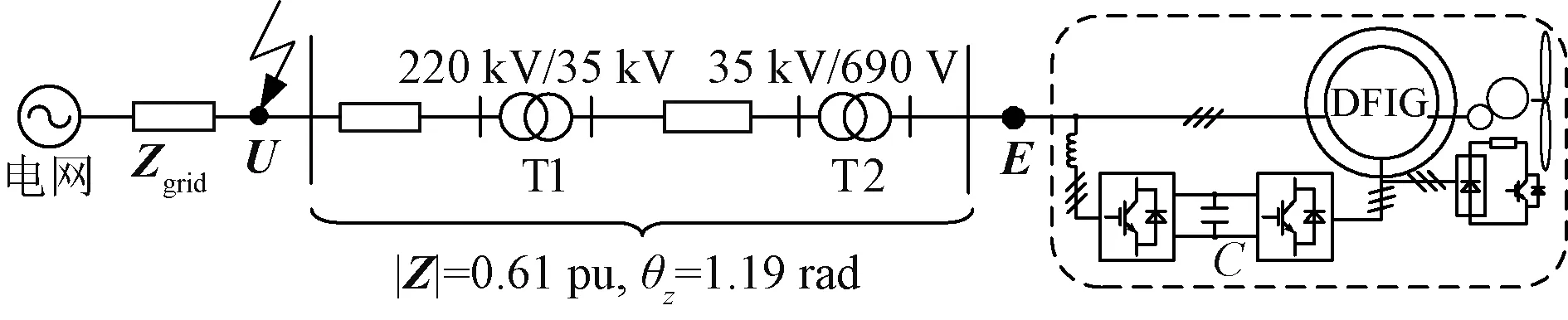
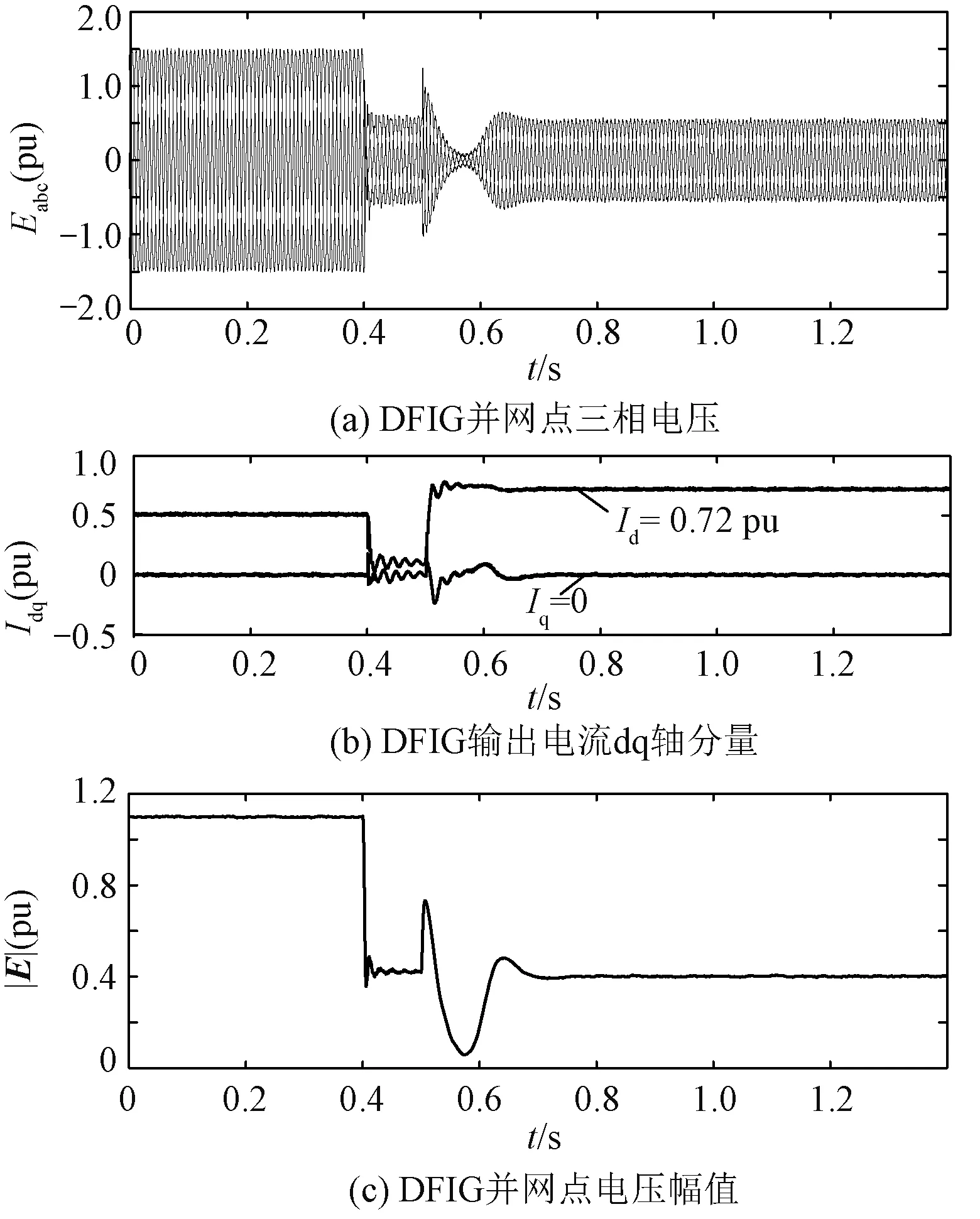



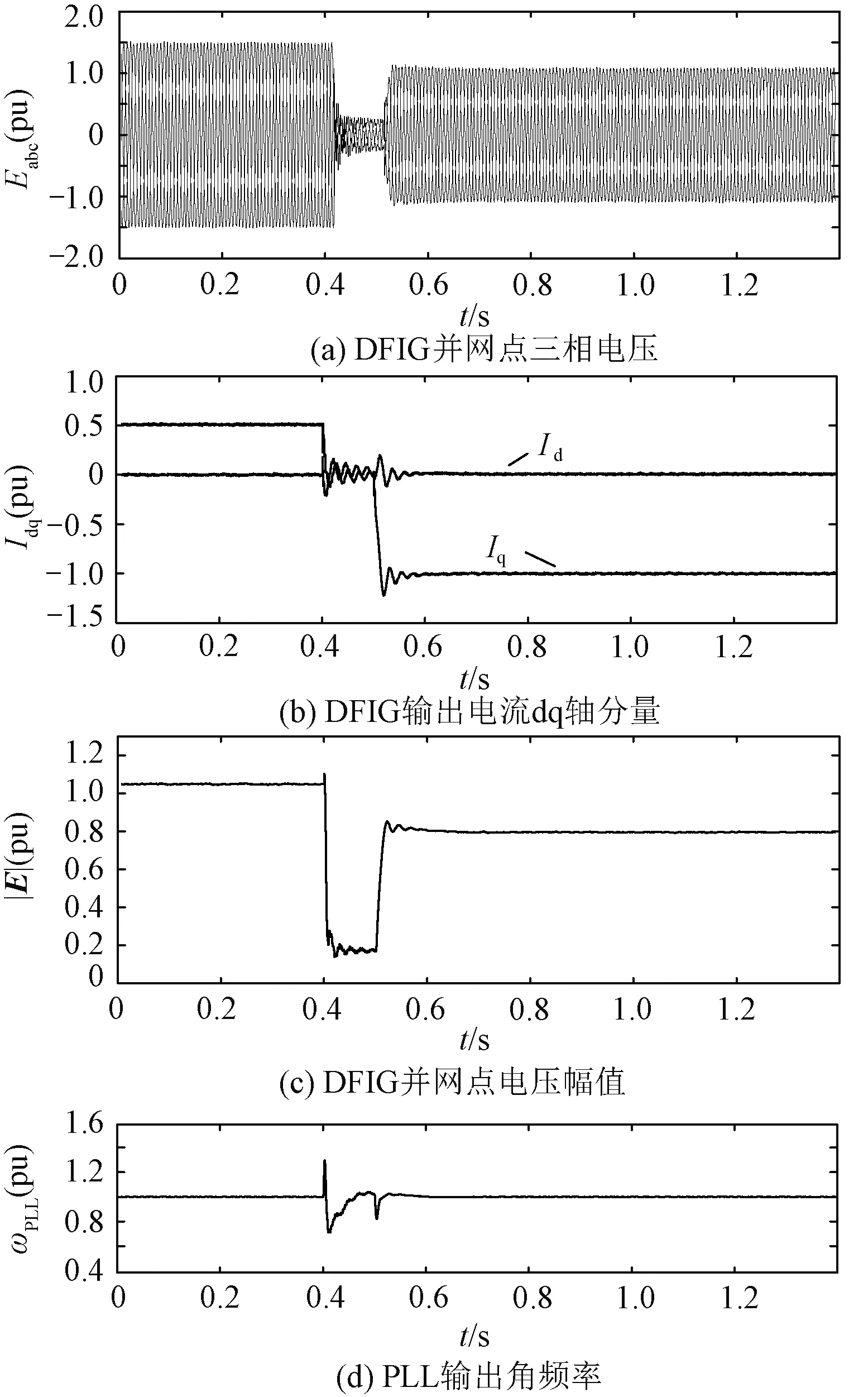


4.2 实验研究


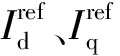
5 结论

