参数曲面理想人造点云生成算法
胡明晓,何才透
温州大学 计算机与人工智能学院,浙江 温州 325035
点云通常是3D设备(如3D照相机、LiDAR)采集的结果。曲面点云的处理在模式识别、机器人、医学影像等领域非常有研究价值,研究人员需要大量的实拍点云进行实验,以检验算法的处理效果和性能。这种实验不仅费时费力,而且成本昂贵。本文提供一种人造点云的生成算法,能够快速、廉价地生成大量带标注3D 点云,以供医学影像处理、逆向工程等研究者检验点云处理算法,为研究人员建立测试数据节省时间和精力[1-2]。同样,在机器学习领域,也存在点云库的需求,大量带标注点云用来测试有监督学习模型的性能和准确度,提高样本训练质量[3-4]。此外,人造点云还可应用于教学、广告、动画设计等领域。
目前,一些物理扫描方式形成的点云库已建立,如斯坦福大学的3D Scanning Repository(http://graphics.stanford.edu/data/3Dscanrep)。本算法面向非物理扫描方式建立大量的带标注点云,即人造点云或点云生成。目前点云生成的研究涉及以下几个方面:基于2D 图像的点云生成、基于已有3D 点云的点云修正(如补全、简化、下采样)、基于曲面方程或模型的3D点云生成(如采样、合成)。
在2D图像的人造点云方面,有许多研究文献报道,其中一些研究使用物理模拟、蓝噪音采样等方法由2D模型生成看起来“均匀”的点云图像[5-7],也有据2D 照片合成3D点云的研究[8]。
生成式点云补全作为一种特殊的修正点云,近几年研究较多,文献[9]采用事件驱动相位噪音方法补全空白;文献[10]讨论了一种基于点素扩散方法(point-voxel diffusion)的3D形状不可见部位点云补全。这些研究结合机器学习补全点云,不要求与事先给定模型相吻合。通过获取模型参数(如密度、曲率)再修正点云亦属人造点云,近年出现的研究有点云简化[11]、点云下采样(down-sampling)[12]等。
基于模型或方程的生成点云,已建有一些静态数据库,如华盛顿大学的OBJ/PLY2PCD 数据库(http://rgbddataset.cs.washington.edu),该库提供一批RGB彩色点云以及3D实体模型OBJ/PLY到点云的转换代码和实例。
3D人造点云方面,用于特定使用场景(如自动驾驶环境)的实时生成算法如文献[13];模拟LiDAR拍摄,自动标注点云的算法如文献[14]。直接基于特定类型3D模型生成点云的研究如Montlahuc 等[15]的CAD 模型模拟点云生成方法,直接以CAD 文件为虚拟物体,生成CAD零件的均匀白噪音点云,同时也能模拟3D摄像机的角度、距离对生成过程进行调节,模拟非理想点云。Chaudhury 等[16]在植物分型(plant phenotyping)研究中亦包含一个基于模型的点云生成步骤,对虚拟植物模型运用类似L-systems 的方法对其表面进行采样,生成白噪音点云。
基于一般3D 模型的点云生成,Corsini 等[17]介绍一种使用约束Poisson 圆盘生成Monte Carlo 蓝噪音点云的方法,该方法适用于曲面的三角网格表示,能产生曲面上均匀的点云。Kang 等[18]根据曲面方程,使用MLS(moving least squares)方法生成均匀、光滑采样的点云,并经曲面重建检验其光滑性,据其实验效果优于VGD(voxel grid sampling)。Huang 等[19]提出一种FPN点云采样方法,不同于一般的随机采样和最远距离采样,而是用快速点云网络将随机初始点驱赶至“最合适”的位置。
以上根据方程或模型生成点云的方法要么直接在精确的3D表面上生成点云,着重于点的精确定位,或者满足一定的光滑性要求,要么仅关注曲面切向的均匀视觉效果,未考虑随机点云的空间蓝噪音化,生成点云不具有厚度。具有厚度尤其是基础真实(ground truth)厚度的理想化点云在检验曲面重建算法和有监督的机器学习中能客观地反映算法性能,在科研领域存在质和量上的需求,出于这一动机,本课题聚焦于生成具有统一厚度的理想化点云。
精确位于曲面上的点云是厚度为零的点云,一旦厚度加大,涉及法向偏移时,高曲率就会影响点云的理想化程度,因此通过以下创新点在切向均匀化的同时实现法向的模式化分布:
(1)曲率偏差现象的分析和曲率补偿;
(2)以法向为主方向的蓝噪音模拟。
本研究目标是根据曲面的参数方程生成曲面切向均匀分布、曲面法向模式化分布、等标准差、各向同性的理想化3D点云,所述模式化分布是指密度函数对称、单调、方差存在的分布,如正态分布、高阶柯西分布。
1 问题描述
参数曲面具有解析性好、形式多样、易于变换、易于插值、能分段拼接形成Bezier 曲面或NURBS 曲面等优点,在几何建模中广泛使用,本文选择参数曲面作为曲面的表示类型。
作为生成点云与之吻合的确定性模型,一般的参数曲面方程为:
其中,u、v为曲面参数。
记一阶导数混合矩阵为:
其中,i,j,k为笛卡尔坐标单位向量。
点p(u,v)处的法向量是:
单位法向量N=n/‖n‖2。
2D参数曲线的方程是:
其中,t为曲线参数。
类似地,3D参数曲线的方程是:
在原理示意时本文有时用曲线来说明。
本研究模拟理想3D扫描仪、LiDAR等3D数字化设备的获取数据,生成人造点云,理想化目标如下:
(R.1)沿曲面(2D时曲线)均匀分布。
(R.2)法线方向点云体密度(2D 时面密度)呈标准差统一为σ的模式化分布(σ2)。
(R.3)3D蓝噪音。
(R.4)各向同性。
2 生成算法
已知参数方程(1)中的函数f,g,h及一阶、二阶导函数。设参数区域为Ω,一般情况下,Ω=[a,b]×[c,d]。如图1,点云生成的顶层步骤由方程预处理、曲面表面点采样、法向模式化分布、曲率补偿和空间主方向蓝噪音模拟组成。在生成过程中,除了指定点数外,还需要指定两个参量:标准差σ和截尾因子λ,前者用来表征统一的厚度,后者用于实现各向同性。模式化分布密度函数为(x)。
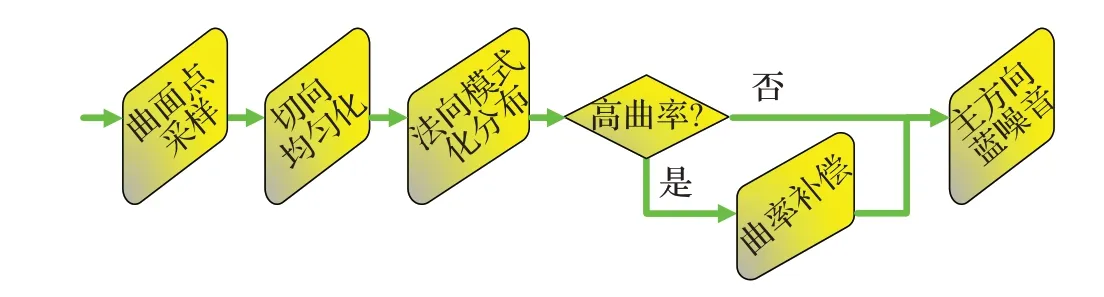
图1 顶层流程图Fig.1 Top-level pipeline
2.1 预处理:参数速度上限估计
曲面的参数速度为面积S的微分:
类似地,曲线的情形更简单,2D 曲线或3D 曲线的参数速度为曲线长度的微分,即:
同样方法可得上限估计值H。
2.2 曲面表面采样
通过参数采样即生成曲面点采样,需要特别处理之处是要做基于参数速度的调节,保证采样点的面密度均匀。为此,引入一个辅助随机变量t。首先,随机产生Ω×[0,H]中的随机3D 点(u,v,t),然后计算s(u,v),再判断t<s(u,v),如果成立,采样,否则放弃,重新产生随机点(u,v,t)。由于参数速度是关于面积微元的变化率,参数速度越快的位置,采样机会越大,容易分析其切向面密度是均匀的,从而实现理想化目标(R.1)。
2.3 法向模式化分布
在曲面采样点周围的3D空间生成3维正态分布的随机点。从理想点云的要求上看,应该在点的曲面法向上等标准差高斯化,即在法向方向产生以曲面点为中心、以σ为统一标准差的一维模式化分布,以高斯分布为例,相对密度函数为:
本文注意到简单情况下3D高斯的叠加能生成法向的高斯或其近似,分析如下。
(1)3D平面点云的情况。不妨设O-XY平面分布有面密度为μ,在各中心点p有服从N(p,σ2)分布的3D点云,其叠加分布的密度函数是:
这说明一组点数相同、标准差均为σ的单点正态分布点云均匀分布在空间平面上,其叠加结果在平面法向的边缘分布上仍服从标准差是σ的正态分布,与切平面平行的任意平面服从均匀分布(f(x,y,z)与x,y无关)。这正是本文想得到的分布。所以只需先产生曲面上点p的均匀分布,再产生点p为中心的3D正态分布,就能满足要求(R.2)。此法无需考虑点p处的法向。
(2)2D 圆点云的情况。不妨设在一个以原点为圆心半径为r的圆上分布有线密度为ρ,在各中心点p有服从N(p,σ2)分布的2D点云。在极坐标系统下,θ处微元dθ处的点数量是ρrdθ,以二维正态分布于整个平面,叠加后的关于(R,Θ)的联合分布密度为:
关于Θ的分布显然均匀,关于R的分布不再是正态分布,利用辛普森数值积分:
可知该分布近似于如下分布:
这仍是以σ-高斯为主的分布,所以这种情况直接将单点3D高斯叠加即可基本满足要求(R.2)。
单点叠加的总步骤是,先参数采样p0(u,v),然后按单点模式化分布律得偏移向量r,最后向量叠加,得采样点p=p0+r。此外,对每个单点的随机偏移,本文进行圆形截尾(2D)或球形截尾(3D),还会使叠加点云各向同性,实现理想化目标(R.4)。以2D 为例,圆形截尾的效果示意如图2(c)。
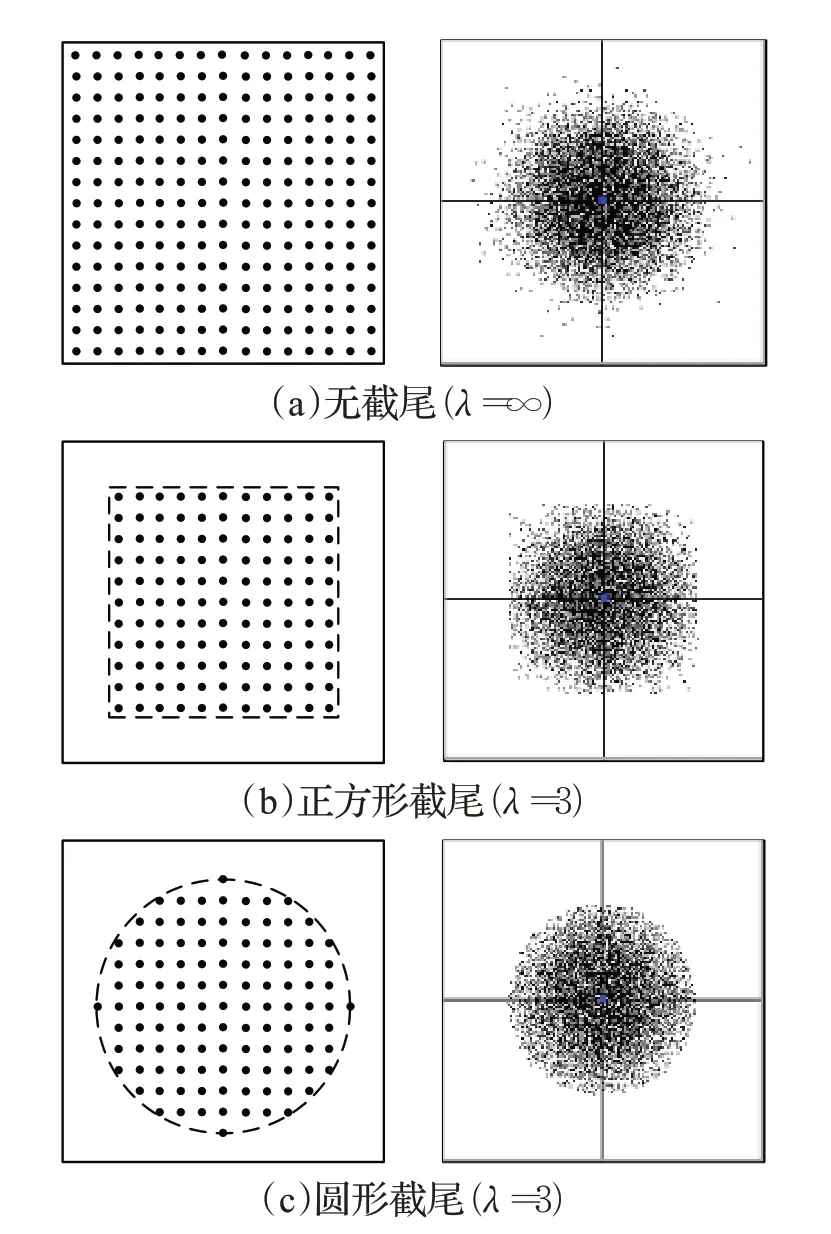
图2 截尾类型Fig.2 Tail-cutting types
2.4 曲率补偿
理想点云的一个重要要求是3D点云体密度(或2D点云面密度)ρ服从关于点到曲面(或曲线)有符号几何距离dG的模式化分布,即:
此种分布才保证点云在曲面高曲率部分呈现均匀的视觉效果。对简单的曲面表面采样和法向模式化分布,曲面高曲率处容易产生曲率中心内侧密度大外侧密度小的曲率偏差现象(如图3)。因此,需要进行曲率补偿,即在高曲率处模式化分布叠加后将一部分曲率中心内侧点搬移到外侧点。
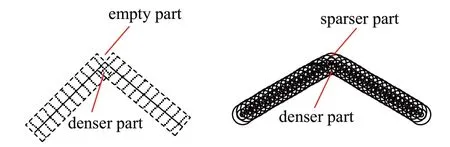
图3 曲率偏差现象Fig.3 Curvature bias phenomenon
以正态分布为例,考虑曲面/曲线上固定点p0,设p0处离曲率中心的法向量为n,曲率半径为R。p是法线上有符号几何距离为x(曲率中心侧为负)的点(如图4),在极坐标系O-rθη(2D时O-rθ)下,r轴上线密度偏差量正比于(x+R)2(2D曲线时(x+R))。因此,用公式(8)调整相对密度函数(2D曲线用公式(9))能纠正偏差。公式(6)、(8)、(9)示意如图5。
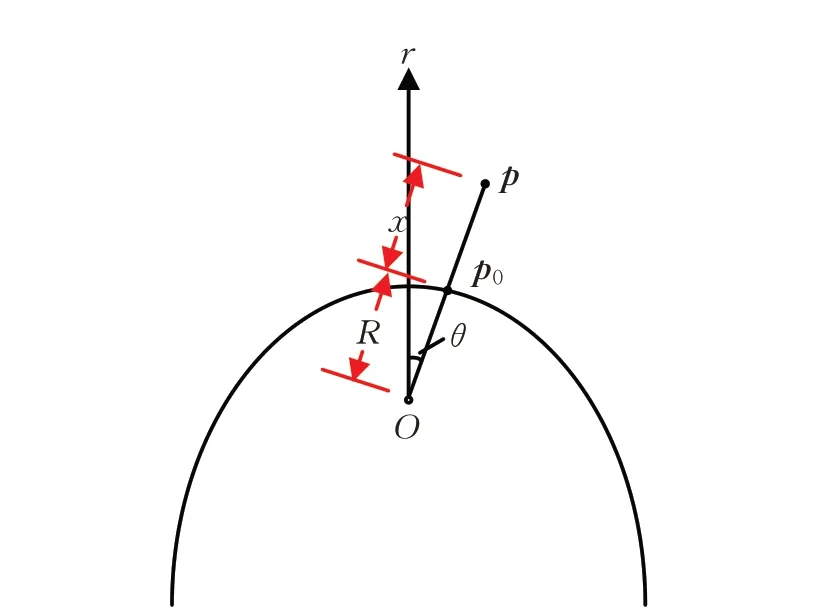
图4 曲率偏差分析Fig.4 Curvature bias analysis

图5 密度纠偏函数Fig.5 Density correcting functions
根据曲面的微分几何,曲面的曲率有主曲率、高斯曲率和综合曲率。随机点云生成依据综合曲率进行曲率补偿是最恰当的。
记二阶导数矩阵为:
在式(1)下,点p(u,v)=(f(u,v),g(u,v),h(u,v))T处的综合曲率Hˉ是[20]:
由此得向心法向量为Sgn()·n。若0,n侧点云应变稀疏,否则n侧点云应变稠密。曲率半径R=|1/|,据式(8)确定补偿率。
实际上,为消除不同模式化分布函数的差异,降低曲率补偿计算复杂性,本文只需估计曲率并分级处理。可作差分近似,如:
图6 表示出分级曲率补偿前后的曲面内外侧密度比的分布情况。
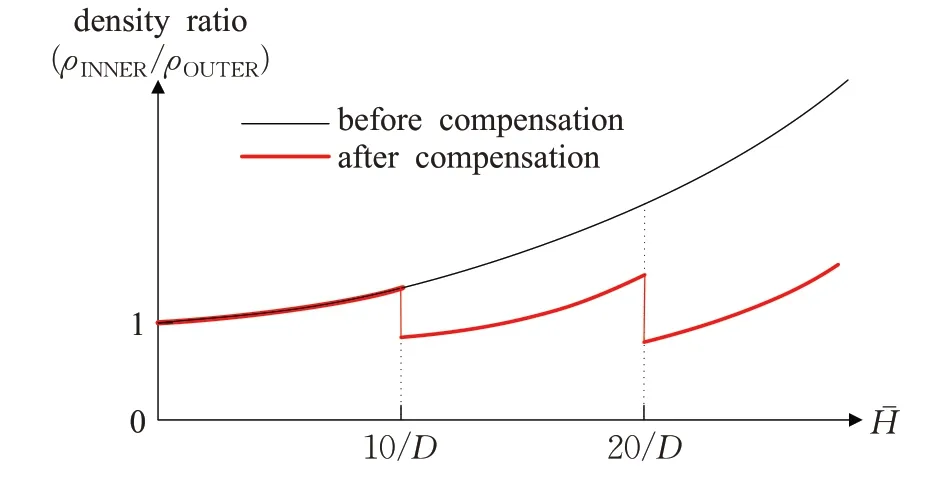
图6 分级曲率补偿效果示意图Fig.6 Illustration of discrete curvature compensation
对2D曲线,先计算曲线曲率:
向量n=(-g′(t),f′(t))T是参数递增方向的左侧法向量。若κ >0,说明n向心,否则离心。Sgn(κ)·n总是向心法向量,再据公式(9)确定补偿率。3D曲线处理方式类似。
法向模式化分布与曲率补偿结合,共同实现了理想化目标(R.2)。
2.5 蓝噪音模拟
理想点云的噪音模拟用单点的三维模式化分布叠加而成,在叠加前采用MBC(Mitchell’s best candidate)方法来模拟主方向蓝噪音,实现点云的理想化目标(R.3)。设噪音标准差为σ,当前点云的点集为P。按照单点叠加的方法连续采样k个曲面参数(ui,vi)和偏移ri(i=1,2,…,k),主方向为点pi=p(ui,vi)处单位法向量Ni。分别计算法向偏移量:
及规范化距离:

图7 单点模式化分布蓝噪音点云Fig.7 Blue noised point clouds with patterned distributions
3 实验结果
本算法用Visual C++.net+OpenGL 代码实现,在2.6 GHz Pentium 双核CPU、2 GB 内存的计算机上进行实验,所涉及曲面/曲线都缩放至边长为6 的包围盒中。对封闭曲面,还限制在边长为4的包围盒中。未加特别说明的法向模式化分布都是高斯分布。
3.1 视觉效果
(1)简单曲面曲线
图8 是由2D 曲线抛物线生成的各种规格点云,点数N=10 000。
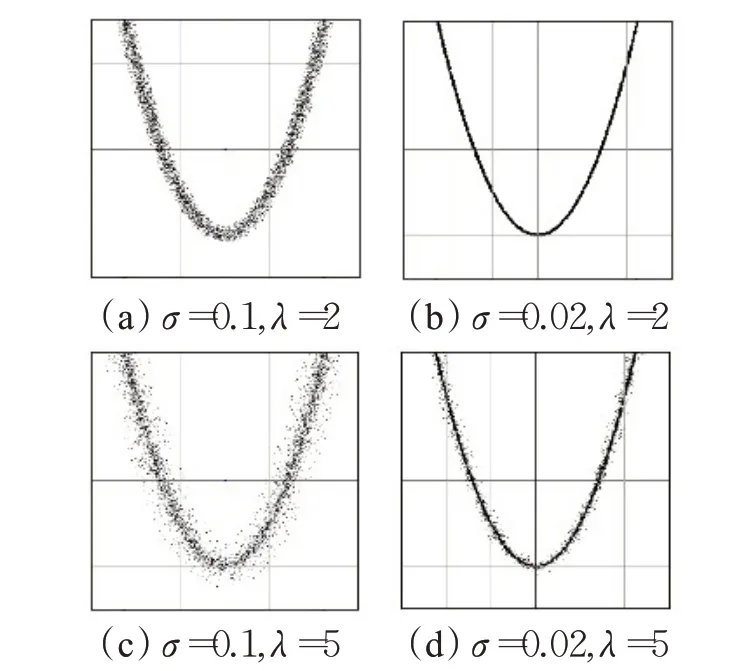
图8 2D曲线生成点云Fig.8 2D curve point clouds
图9是由3D曲线莫比乌斯带边缘线生成的各种规格点云,点数N=10 000。

图9 3D曲线生成点云Fig.9 3D curve point clouds
图10 是由同一环面生成的各种规格点云,点数N=20 000。图11是不同环面生成的同种规格点云,其中环面的两个半径参数相对变化,从R=1.25,r=0.25开始,将r逐渐增大直至1.25 产生奇点,生成点云一直保持均匀的视觉效果。

图10 曲面生成点云Fig.10 Surface point clouds

图11 不同参量曲面生成点云Fig.11 Surface point clouds on different parameters
(2)复杂曲面
具有简单解析式曲线曲面的生成点云视觉上达到理想的均匀分布效果,而任意复杂曲面可用三角网格表示,其中每个面片可以参数化,由此亦能生成理想点云,以Bunny Rabbit(N=50 000)和Utah Teapot(N=50 000)为例,各种规格点云如图12、13。
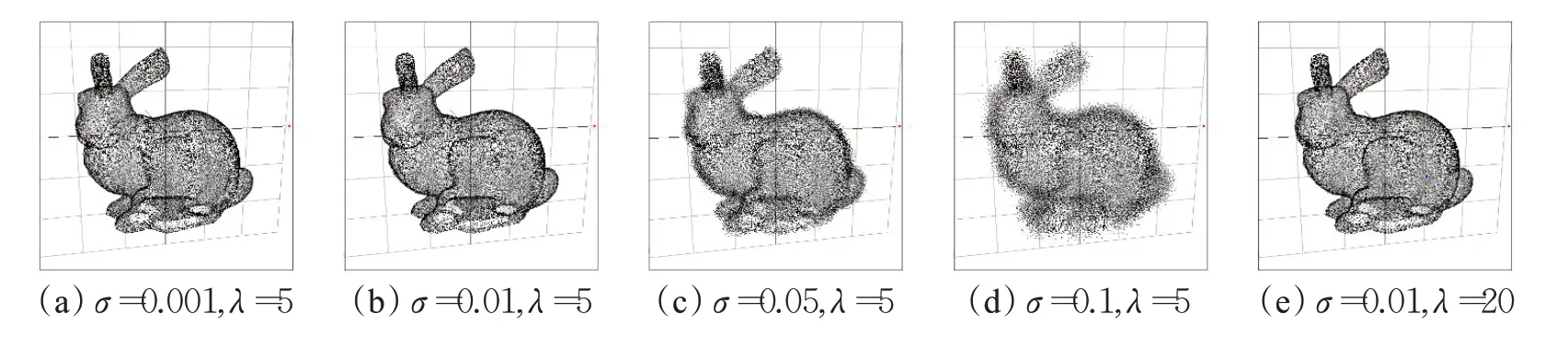
图12 三角网格曲面生成点云(一)Fig.12 Triangular meshed surface point clouds(1)

图13 三角网格曲面生成点云(二)Fig.13 Triangular meshed surface point clouds(2)
(3)开放曲面
封闭曲面是3D实体的表面,除了封闭曲面之外,开放曲面的点云也能够生成。图14是由开放曲面生成的点云结果,点数N=50 000。

图14 开放曲面生成点云Fig.14 Open surface point clouds
(4)非理想点云
为了与理想结果对比,本文生成一组非理想点云与理想点云图12(b)对比。如图15,(a)呈现条纹,非各向同性;(b)法向非模式化分布(均匀分布);(c)未经曲率补偿,高曲率处内外密度有偏差;(d)局部点集不均匀,非蓝噪音采样。3D点云(b)(c)肉眼较难分辨其不同之处,下一节给出量化对比。为更清晰展示理想点云的视觉效果,图16给出一组2D情形的对比点云,其中(b)为理想点云,易见已基本消除高曲率处的密度偏差,(c)为法向非模式化分布,(d)为未曲率补偿,易见其在顶端高曲率处的非理想结果。
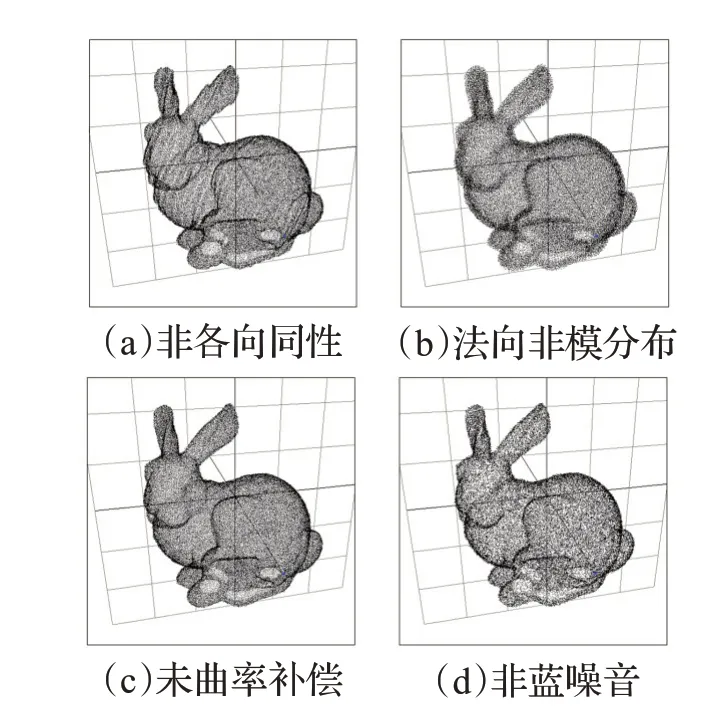
图15 非理想点云(σ=0.01,λ=5)Fig.15 Unqualified point clouds(σ=0.01,λ=5)

图16 非理想2D点云Fig.16 Unqualified 2D point clouds
3.2 量化指标比较
实验结果用两个指标度量3D 曲面点云:面密度和厚度。面密度表征曲面切向密度,定义为曲面上小邻域内的点的数量与邻域面积之比:ρ=N/S。厚度表征点云在曲面法向的噪音强度,与标准差关系密切。由于[-d,d]噪音均匀分布时标准差是,因此,对噪音呈σ-模式化分布,用作为厚度。
点云中每个点的ρ和h都一一计算,方法如下:取点pi,根据测地距离构造邻域点集(方法如Cartesian grid based(CGB)[21]),假设点集包含ni个点,由圆并集面积算法得邻域面积Si,于是
然后构造scatter矩阵[22],计算特征值,由于scatter是半正定对称阵,特征值必非负,取最小特征值λi,即得标准差:
及厚度:
(1)与真实指标比较
面密度和厚度的基础真实值ρT、hT容易通过参数曲面及其参数范围事先计算,它们都是全局指标。厚度与标准差只差一个常数因子,故下面直接比较标准差。对生成的点云,按上述方法计算每个点的指标后,再根据以下两式计算全局平均值:
表1(相应图如图17)列出3.1节大部分点云的全局平均密度和全局厚度与基础真实值的比较,部分模型点数有增减,厚度仅用标准差代替。与基础真实值相比,10个模型中有5个模型,全局密度的相对误差在10%以内,7 个模型在30%以内;关于厚度,则有4 个模型相对误差在10%以内,7个模型在30%以内。可以看出,指定的标准差ρT在0.001~0.1范围内生成点云的误差很小,过小(≤0.001)或过大(≥0.1)都不利于理想点云的模拟。
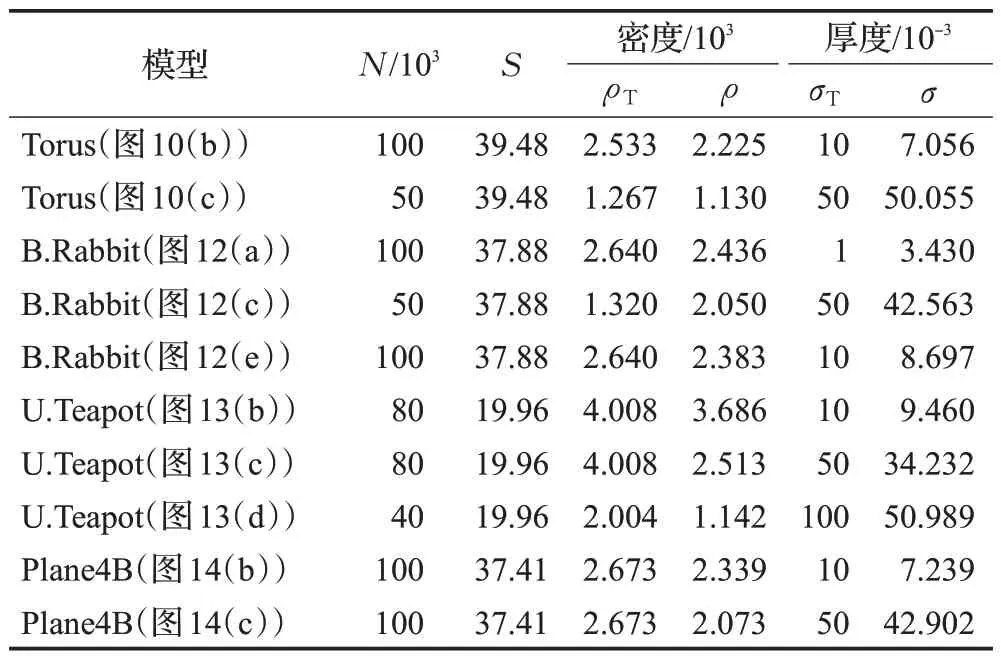
表1 与真实值的比较Table 1 Comparison to ground truth

图17 与基础真实值的比较Fig.17 Comparison to ground truth
(2)与其他方法比较
依据参数曲面生成理想点云时,期望点云的面密度处处相同,厚度亦然。所以本文比较点云各点的局部面密度ρi=Ni/Si的均等程度,方案是选择各种方法的一组实验模型,对每种方法,每个模型的密度分布的均值都归一化到单位1,再对各模型的归一化分布作总评,得到单一分布,作为该方法的数量化表达。
对每种方法,计算面密度、厚度的总评(Summerized)分布标准差σρ、σσ,标准差越小说明均等程度越好。
归一化处理可以合理地在不同模型、不同方法之间进行点云生成质量比较。本算法参与总评的点云模型来自3.1节。CAD Assembly模型来自文献[15]的表格,括号中注明的是表号和行号。Plant Phenotyping 模型来自文献[16]提供链接的4个下载文件,分别是:
Lilac1:Lilac_2Labels_onlyPoints.xyz
Lilac2:Lilac_multilabel_onlyPoints.xyz
Arabido.1:Arabidopsis_1_onlyPoints.xyz
Arabido.2:Arabidopsis_4_onlyPoints.xyz
面密度和厚度比较如表2,列出两种方法(plant phenotyping 和CAD assembly)和本算法归一化后的标
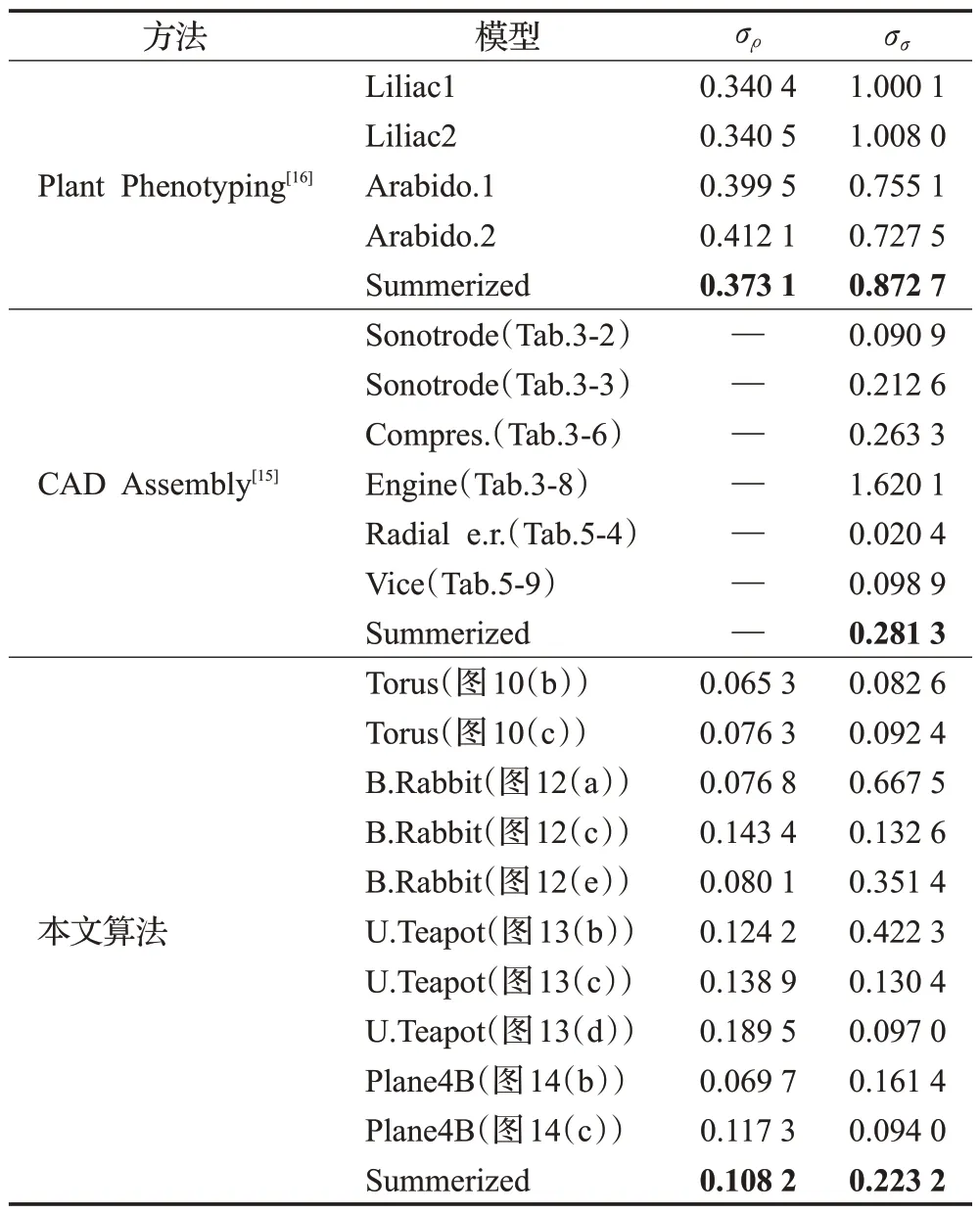
表2 密度厚度均匀性比较Table 2 Comparison of density and thickness uniformity
注:来源附于模型名之后,例如:Tab.3-8表示来自文献[15]Table 3第8行。准差,本文的密度和厚度分布标准差都最小(σρ=0.108 2,σσ=0.223 2)。

表3 与非理想点云的量化比较Table 3 Quatitative comparison to unqualified
图18 是密度分布情况,其中将[0,3σ]等分成22段。从图中可看出,本算法不但标准差小(非常集中),而且偏度亦小(对称性高),说明分布十分理想。
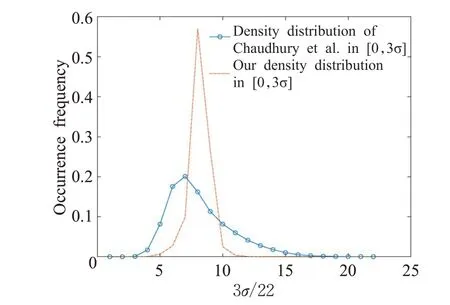
图18 密度分布比较Fig.18 Comparison of density distribution
图19是厚度分布情况,将[0,12σ]等分成22段。图中可看出,本算法厚度分布标准差也小(比较集中),且偏度小(对称性高),说明分布比较理想,点云的厚度基本上处处统一。
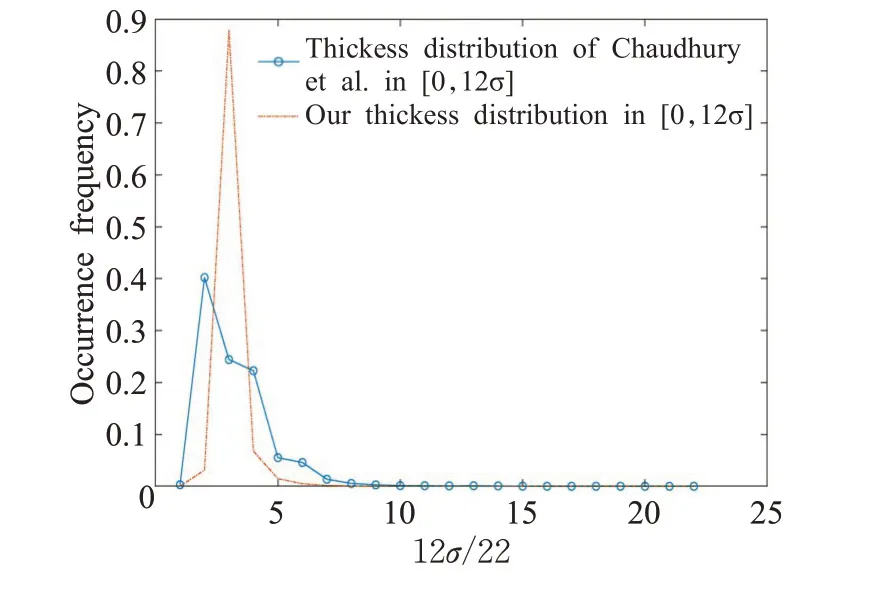
图19 厚度分布比较Fig.19 Comparison of thickness distribution
(3)与非理想点云比较
对肉眼不易辨别的非理想点云(图15(b)(c)),特别给出定量比较,如表3,列出它们的面密度、厚度的相对误差eρ、eσ(与基础真实比较)和分布标准差σρ、σσ,其中图12(b)是本算法的理想化点云。
表3 中显示,理想点云在视觉效果占优的同时,数量指标总体亦较优,尤其是相对误差,均为最优。标准差略有损失,但不严重。
4 结束语
由参数方程生成理想点云的算法能以低成本生成人造点云,本算法能够使人造点云模拟理想3D 扫描仪的拍摄结果,具有视觉上的“均匀性”,具体上说,面密度均等,法向同标准差分布,空间蓝噪音,各向同性,高曲率处内外密度偏差小。基于这些特征,通过本算法能以低成本建立点云库,而且易获取伴随点云的基础真实值并加标注,从而为3D 曲面重建的算法测试和机器学习的有监督学习提供大规模的基础数据。

