费曼路径积分强场动力学计算方法*

刘希望 张宏丹 贲帅 杨士栋 任鑫 宋晓红† 杨玮枫3)‡

1) (海南大学物理与光电工程学院,海口 570228)

2) (汕头大学理学院,汕头 515063)

3) (海南大学理论物理研究中心,海口 570228)

1 引言

现代量子力学始于2 个不同的数学公式,薛定谔的微分方程[1]和海森伯的矩阵力学[2].1948 年,费曼将最小作用量原理应用到量子力学中,提出了一种完全崭新的量子力学表述-费曼路径积分方法[3].不同于薛定谔方程从微分波动方程的角度,费曼从路径积分和经典作用量的角度来处理问题,将时间分割为许多小时间段,以经典拉格朗日量作为相位的传播算子,将所有到达 (x,t) 的路径贡献叠加便能得到波函数φ(x,t),这已被证明满足薛定谔方程.虽然看待问题的角度不同,但是2 个方程在数学上是等价的,量子力学中的概率概念没有改变[4].该方法不仅为经典力学和量子力学架起了一座新的桥梁,同时还为量子力学、场论和统计模式提供了一个统一的观点.

1960 年,世界上第一台红宝石激光器问世[5],激光飞速发展.激光具有很高的光强,与物质相互作用会产生各种非线性的物理现象.这些非线性的物理现象与微观粒子结构性质具有很强的依赖性,通过研究这些现象可以探索微观世界动力学过程,同时也能得到微观粒子的结构信息.但是这些非线性的物理现象也为理论研究提出了巨大的挑战[6−8].显然,经典动力学模型在微观世界已经不再适用,量子力学的出现为研究微观世界提供了有力工具.强场动力学的理论研究最早可以追溯到由Keldysh[9],Faisal[10]和Reiss[11]提出的KFR 理论,该理论被广泛用于解释强激光场下的实验现象.在KFR 理论的基础上,研究者又考虑各种效应并发展了不同的理论模型,这些模型统称为强场近似(strong field approximation,SFA)方法.1966 年,Perelomov,Popov 和Terent’ev[12]推导出电子任意束缚态的电离率—PPT 理论.1986 年,Ammosov,Delone 和Krainov[13]简化了PPT 理论得到准静态绝热近似下的电子电离率—ADK 理论.1994 年,Lewenstein 等[14]提出了基于费曼路径积分方法与拉格朗日最小作用量原理的全量子SFA 理论,且使用该理论研究了低频激光产生高次谐波.这些开创性的理论为各种强场全量子动力学、半经典动力学与经典动力学计算方法提供了指导性意义.

求解全量子含时薛定谔方程(time-dependent Schrödinger equation,TDSE)[15,16]可以获得精确的电子波包演化,进而根据每个时刻的波函数求得电子的速度分布或能量分布,但是由于其没有解析解,只能借助计算机在每一时刻演化多维的微分方程得到数值解.基于费曼路径积分的强场动力学方法将波函数用不同状态的粒子描述,通过将不同粒子的贡献相干叠加来描述电子动力学过程.SFA模型用平面波戈登-沃尔科夫态 (plane-wave Gordon-Volkov states) 来描述电子在连续态中的运动,忽略了束缚势的影响.正是由于SFA 方法忽略了库仑势的作用,其结果与实验和数值求解TDSE的结果很难在定量上完全一致.为了克服SFA方法的局限,研究了各种改进方案.例如,库仑沃尔科夫近似 (Coulomb-Volkov approximation,CVA)[17,18]用库仑扭曲波替代了平面波,该方法经常被用来研究光电子谱[19,20].库仑修正强场近似(Coulomb-corrected strong field approximation,CCSFA)[21,22]在SFA 的作用量中引入微扰的库仑效应对相位进行了修正,其电子轨迹并没有受到库仑势的影响.基于轨迹的库仑修正强场近似 (trajectory-based Coulomb corrected strong field approximation,TCSFA)[23,24],将库仑势的影响引入作用量与电子连续态运动过程中.库仑量子轨迹强场近似 (Coulomb quantum-orbit strong field approximation,CQSFA)[25,26]是从费曼路径积分公式中使用时间演化算子的函数积分表示的方法,求解连续态中完整的库仑运动方程,忽略了隧穿过程中轨迹的库仑效应.

相较于TDSE,费曼路径积分强场动力学计算方法模型简单计算效率更高,同时由于电子被看作具有不同初始状态的粒子,从而可以根据经典牛顿方程追溯每个粒子的运动轨迹,通过解析粒子的运动状态便能发现各种物理现象的产生来源,已在强场动力学计算中被广泛使用,并用于分析强场物理中的各种新奇的实验现象[27,28].Salières 等[29]利用费曼路径积分方法复现了高次谐波谱(high-order harmonic generation,HHG)和阈上电离谱(abovethreshold ionization,ATI).Huismans 等[30]通过精确求解TDSE 与CCSFA 在亚激光周期时间尺度上观察到电子动力学的全息结构,并且通过分析轨迹发现不同干涉结构源自不同轨道的相干.Li 等[31]基于费曼路径积分思想在经典轨道蒙特卡罗(classical trajectory Monte Carlo,CTMC)方法[32]基础上采用ADK 理论,并且赋予每条轨道相位信息发展出量子轨迹蒙特卡罗(quantumtrajectory Monte Carlo,QTMC)方法,并研究了光电子谱中的阈上电离结构.Shvetsov-Shilovski 等[33]修正了QTMC方法的相位提出了半经典两步模型(semiclassical two-step model,SCTS),通过相位修正使得低能部分的计算更加精确.Song 等[34]在QTMC 的基础上采用非绝热电离率发展了推广的量子轨迹蒙特卡洛方法(improved quantumtrajectory Monte Carlo,IQTMC).Liu 等[35,36]采用分子ADK 理论发展了分子量子轨迹蒙特卡罗方法,提取了分子隧穿波包的相结构,证明了隧道出口处的隧道波包的初始相位与初始横动量分布和分子核间距有关.Gong 等[37]通过实验与非绝热QTMC 方法观测到氩原子从4f 态与5p 态的光电子发射存在大约1.4×10−16s 的费曼共振时间延迟.Song 等[38]通过相位-相位 (phase of phase) 技术结合非绝热QTMC方法证明了电子可能从连续态被捕获到束缚态并在该束缚态上停留一段时间再电离出去,且该停留的时间大概是几百阿秒.同年Porat 等[39]通过实验结合CCSFA 方法以阿秒精度重建了形成光电子全息图中光电子的电离时间,通过将全息图两个臂的贡献解耦发现其电离时间差仅为几十阿秒.Trabert 等[40]在实验上观测到了氢分子隧穿电离中的Wigner 时间延迟随电子发射与分子轴夹角的关系,并且通过求解TDSE,SCTS 与SFA 模型验证了该结果的可靠性.Torlina等[41]将势垒下的库仑势引入鞍点方程发展了解析的R 矩阵(analytical R-matrix,ARM)理论,并且利用该方法重新定标了阿秒钟,证明了隧穿过程是瞬时的.Tong 等[42]在TCSFA 的基础上修正了鞍点方程提出自参照分子阿秒钟的新思路,成功测量了电子在二聚体分子共振态上的停留时间.Yan和Bauer[24]在连续态充分考虑库仑势的作用,同时在势垒下的作用量也考虑了库仑势作用发现TCSFA 和TDSE 结果能定量符合.

可见费曼路径积分强场动力学计算方法已在强场物理中被广泛使用,很好地重复并解释实验现象,弥补了TDSE 无法给出清晰物理图像的缺点,同时简化了计算模型使得计算的可行性大大提高.但是费曼路径积分强场动力学计算方法也存在一定的局限性与不足,费曼路径积分完全等同于薛定谔方程需要考虑所有的可能轨迹(不仅仅是经典轨迹,也包括量子轨迹).受限于计算能力,往往采用大量轨道模拟,由于轨道计算不够导致与真实结果可能存在一定偏差.同时,不同模型对于初始条件的选取也存在差异,导致不同模型对于相同的问题结果也会有所差别.例如,在SFA 模型中不考虑库仑势的作用导致结果很难在定量上与实验符合,一般用于定性验证.在求解电子连续态的运动轨迹时,往往采用龙格-库塔法求解,但是在靠近核附近容易产生奇点,使得该轨迹无法求解.所以针对不同的问题需要选择合适的理论模型与计算方法.

本文将系统地介绍基于KFR 理论的SFA 计算方法.首先简要介绍SFA 的基本理论,如偶极近似和鞍点近似等.然后重点介绍电子跃迁振幅的推导,详细介绍CCSFA,TCSFA 和CQSFA 方法的推导及应用.最后对费曼路径积分强场动力学计算方法的发展趋势进行展望.除特殊说明外,本文均使用原子单位,即 ℏ=e=me=1 a.u.

2 基本理论

2.1 偶极近似

在SFA 模型中通常会考虑偶极近似,当激光场的波长λ远大于模型系统的距离和电子的漂移距离d时(λ ≫d=E0/ω2,E0与ω分别为激光的振幅和频率),矢势A(r,t) 中的空间分量可以被忽略.即有A(r,t)→A(t),这种近似可以使哈密顿函数更容易求解,同时在合理参数范围内对人们所感兴趣的物理现象没有明显的影响.磁场表示为B=∇×A(r,t),由于忽略了矢势的空间分量,那么该磁场的值将为0,也就是说该近似导致模型同时也忽略了磁场的作用.

2.2 长度规范与速度规范

考虑偶极近似下的激光与原子分子相互作用,通常用到两种规范[43]: 长度规范与速度规范.在数值求解TDSE 时规范不变性已被证实,但是求解TDSE 不能够分析这些物理现象.为了分析这些物理现象,研究者通常会采取不同的近似模型,其中最常用的就是SFA 模型.但是看似非常合理的近似之后缺乏规范不变性,在SFA 模型中一般情况下两种规范下会得到不同的结果,其中Bauer 等[44]详细讨论了SFA 模型中的规范问题.

在单电子近似下,对于一个固定的原子核,除其中一个价电子外的所有电子作用都被当成一个有效的束缚势.此时这个电子与电场的耦合可以用哈密顿量来表示:

其中,下标 (x=L,V) 代表不同的规范;H0=表示无场下的哈密顿量(me为电子质量),束缚势V(r) 与选择何种规范无关.在偶极近似下,认为电场在空间中是均匀的,忽略了电场E(r,t) 的空间依赖,因此E(r,t)→E(t),A(r,t)→A(t).电场的相互作用项在不同规范下可以表示为

其中,r与p分别为电子的空间位置与速度.当电子运动到足够远且电场强度足够大时,此时电子所感受到的束缚势的作用远小于电场的作用,电子将被近似地看作在电场中运动的自由粒子,自由电子哈密顿量表示为

(1)式哈密顿量的含时演化算子Ux(t,t′) 满足Dyson 公式:

式中,Ux(t,τ) 为中间态演化算子,U0(t,t′) 为无场哈密顿量H0的演化算子.电子从电离能为Ip的束缚态|ψ0(t)〉=|0〉exp(iIpt) 到连续态|ψp(t)〉的电离振幅写为

将(1)式代入(5)式,由于初态和末态的正交性第一项为0,可以得到以下结果:

由于考虑SFA,即认为电子电离后将不受到束缚势的影响,此时电离的电子可以用沃尔科夫态来表示.那么在任意时刻〈ψp(τ)|Ux(t,τ)=,(6)式可以写为

这样即得到电子从初态电离到连续态的几率振幅,其中连续态电子可以用沃尔科夫态表示为

2.3 鞍点近似

鞍点近似方法也被称为最速下降法[45],是一种积分近似的方法,在数学及物理等领域有广泛应用.例如求解非线性方程组[46]、X 射线结构分析[47]、机器学习[48]和量子力学[49]等.求解类似如下复平面内的积分:

式中,C为复z平面的固定曲线,而g(z) 和w(z)是包含C的某个区域D中的解析函数.只要I(λ)是收敛的,积分在路径C的端点是允许存在奇点的.对曲线C做一个变形使其通过w(z) 的鞍点z0,并且沿最速下降方向离开鞍点,将 exp[iλw(z)] 在该鞍点处展开,由于w′(z0)=0 那么其得到的剖面在保留二次项的条件下近似为高斯函数:

为了确定最速下降方向,可以利用复数的极坐标形式:

其中,α与θ为相角,ρ为径向距离,可以得到

由(12)式可知w(z) 的实部在α+2θ=2nπ 时增长最快.反之,当α+2θ=(2n+1)π 时实部为最速下降.因此可以通过由以下条件确定最速下降方向:

g(z)通常是缓慢变化的函数,将(10)式代入(9)式可得:

根据高斯积分再将所有鞍点求和可得:

因此,这将会产生N个鞍点方程,其形式如下:

进行多变量泰勒展开和计算N个高斯积分可得

这里,w′′(z1s,z2s,···,zNs) 代表多变量作用量的海森矩阵.为了不失一般性,需要考虑无限维的情况,此时函数形式为

那么其鞍点方程写作 δw[zs]=0,将作用量w[z] 泰勒展开到二阶项可以得到:

这里,δzs(t)=z(t)-zs(t).将(19)式代入(18)式得到

同理对上式使用高斯积分可以得到

2.3.1 数值计算鞍点方程

对于简单激光场,可以很容易得到鞍点ts的解析形式.例如线偏振激光场E(t) 形式为∫Ez(t)=E0sin(ωt),那么根据其矢势A(t)=-E(t)dt可得

其中A0=E0/ω,E0为电场强度,ω为电场频率.将(21)式代入鞍点方程可得

其中,px,py,pz分别为电子三个方向的渐进动量.将(22)式化简可得ts有2 个解:

由于Im[ts]＞0,所以(23)式的±只取-.虽然(23)式很容易计算出其鞍点值,但当电场形式为更复杂情况时,例如矢势形式如下:

将(24)式代入鞍点方程很难给出鞍点的解析表达式.由于无法给出鞍点的具体表达式,做数值计算时可以考虑在一定区域内均匀地给出试探解,记录误差在可接受范围内的解.但是这将耗费大量时间,而且得到的解精度各不相同,需要更高精度就需要更加密集的试探解,同时将带来更大的计算量.

2.3.2 遗传算法计算鞍点方程

为了解决这个问题,一种基于遗传算法的CCSFA 方法被提出[51].令目标函数

当函数f(t)=0 时,满足鞍点方程.遗传算法流程如图1 所示,具体可分5 步来求解该方程.

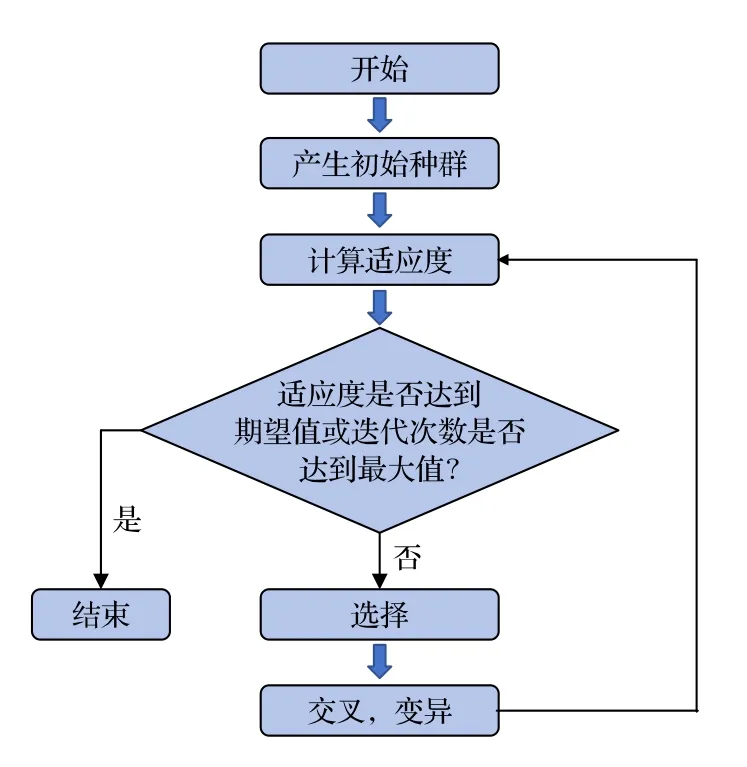
图1 遗传算法流程图Fig.1.Flowchart of genetic algorithm.

步骤1产生初始种群.这个过程开始于一组随机生成的个体样本,其中每个样本都是问题的解决方案.样本的特征是由一组基因决定的.基因通常用0 和1 组成的二进制编码表示.由于鞍点方程的解为复数ts=tr+iti,所以为每个样本采用2 个基因,分别代表ts的实部和虚部.种群规模应该尽可能大,因为初始个体越多,进化出最佳结果的可能性就越大.

步骤2重构一个适应度函数H=1/(|f(t)|+0.01),并计算每个个体的适应值,当函数f(t)=0时,其适应度最高Hmax=100.选出其适应度满足给定条件的样本,例如当H ＞99,此时|f(t)|＜10-4.适应度函数评估种群中每个个体样本的适应度,该个体被选择繁殖的概率是基于其适合度分数.

步骤3选择.从当前的种群中,根据其适应度分数,提取作为父母的基因子集.每个样本被选择概率记为,其对应着在0—1 区间的长度.随机生成0—1 的随机数,当该随机数落在该个体对应的区间时,则选择该个体样本.

步骤4交叉、变异.交叉就是对上一步所选择的个体样本两两配对,将对应两个样本的同一个基因选择一段尾部编码进行互换.这样交叉后既保留了上一代的主要性状,同时又产生了新的特性.变异是将产生的新个体在基因序列上随机选择一个二进制编码改变.不需要每个个体都发生变异,只需要选择很小一部分个体样本进行变异.

步骤5至此就产生了新一代的样本,如果适应度达到期望或迭代次数达到最大值,则停止产下一代,否则就从步骤2 开始重复整个过程.

遗传算法在本质上是非遍历性的,所以其搜索解的效率很高.但是变异概率、交叉概率和种群大小等参数对遗传算法的性能有重要影响.非常小的突变率可能导致某些解的遗漏,过高的突变率可能会导致好的解丢失并且算法很难收敛.通常情况下能得到多于目标个数的解,这时需要排除多余的解.所以需要在一定范围内挑选一个适应度最大的解作为目标解.

2.3.3 牛顿迭代法计算鞍点方程

牛顿迭代法是一种在实数域或复数域上为方程找到近似解的方法,常用来求方程根,其最大优点是在方程f(x)=0 的单根附近具有平方收敛性.设x*为f(x)=0 的根,在空间内选择任意x0作为x*的试探解,过 (x0,f(x0)) 点作曲线y=f(x) 的切线L:y=f(x0)+f′(x0)(x-x0),则L与x轴交点x1=x0-f(x0)/f′(x0),那么x1为x*的一次近似值.如图2 所示,根据新得到的横坐标重复以上过程不断求切线与x轴的交点,可以得到xn+1=xn-f(xn)/f′(xn) 为xr的n+1 次近似值.通过不断迭代xn+1,将会越来越接近方程的根x*.

图2 牛顿迭代法图示.蓝色曲线为方程 f(x) 的解,红色直线为蓝色曲线在自变量 x 处的切 线,x* 为方程f(x)=0时需寻找的解Fig.2.Illustration of Newton’s method.Blue curve represents value of function f(x),and red lines represent tangent to blue curve at independent variable x,which is solution x* when f(x)=0.

下面介绍用牛顿迭代法求解鞍点,同理将鞍点方程以函数表示:

对(25)式求导可得

在复平面时间内均匀采点作为迭代的起始点,通常一个时间周期T只需采样很少的点(为了不漏解,在实轴方向 0→T采样5个点,虚轴方向0→100 a.u.采样2 个点).因为f(t) 是连续的,那么在零点周围存在一个区域,只要初始值位于这个邻近区域内,那么牛顿法必定收敛.以采样点t(0)为例,那么ts的一次近似值为

以此类推,可以得到

以实例来说明该过程,随机采样3 个方向的速度为

矢势形式如下

根据E(t)=-∂A(t)/∂t得

选择4个初始试探解分别为 (tr=20.1,ti=80.1),(tr=40.1,ti=80.1),(tr=60.1,ti=80.1),(tr=120.1,ti=80.1).计算结果如图3 所示,其收敛性呈指数型增长,可以看到仅仅需要迭代不到10 次,其计算精度就达到了 10-15.

图3 4 个样本的 |f| 随迭代次数的变化.蓝线、橙线、黄线和紫线分别代表初始试探解为 (tr=20.1,ti=80.1)、(tr=40.1,ti=80.1),(tr=60.1,ti=80.1) 和(tr=120.1,ti=80.1) 时,随迭代次数增加函数值 |f| 的变化.Fig.3.Variation of |f| with the number of iterations n for four samples.The blue,orange,yellow,and purple lines represent the changes in function values |f| with increasing iteration times when the initial trial solutions are(tr=20.1,ti=80.1),(tr=40.1,ti=80.1),(tr=60.1,ti=80.1) and (tr=120.1,ti=80.1),respectively.

同样地,由于采样数一般会多于实际目标解的个数,所以会有一些重复的解,需要排除多余的相同解.对比于遗传算法,牛顿迭代法更适用于求解鞍点方程的近似解,因为其不依赖于设置参数,而且迭代是基于上次计算结果有方向的搜解,通常情况下只需要迭代不到10 次便能达到很高的精度.

2.3.4 鞍点方程修正

在SFA 中,作用量S通常忽略库仑势的影响,考虑库仑势的情况下作用量为[41]

其中鞍点方程的解ts=tr+i·ti为一个复时间,这样积分路径可以分为两项:

这里,第1 项为势垒下沿着虚时间轴的隧穿动力学过程 (ts→tr);第2 项为沿着实时间轴的连续态传播 (tr→∞).在鞍点近似方法中,SV(p,t) 的被积函数在复数域为一个解析函数,其积分与路径无关:

然而,当r靠近0 时,V[r(p,τ)]=z/r(p,τ) 不是一个解析函数,其积分与路径有关,所以(30)式的第2 项不能像(32)式一样直接得到.为了解决这个问题需要将积分路径分为两部分[42]:

这里等式右边第1 项代表在复平面内势垒下的隧穿动力学 (ts→tr),第2 项代表隧穿后在连续态中的传播 (tr→∞)(图4).这样(30)式中的库仑作用项可以写作

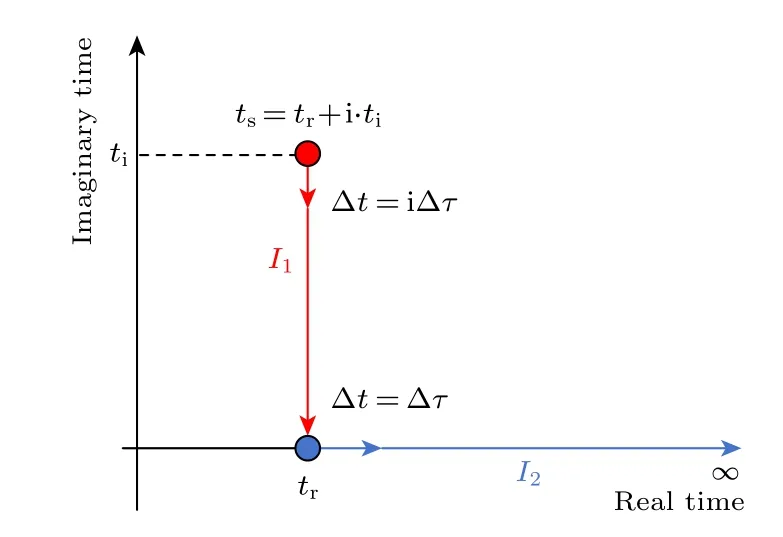
图4 复平面的路径积分.I1 描述了沿虚时间轴的积分,步长为 iΔτ .I2 描述了沿实 时间轴的积分,步长为ΔτFig.4.Path integral on complex plane.I1 describes integration along imaginary time axis with a step size of iΔτ,and I2 describes the integration along real time axis with a step size of Δτ.

在复平面内,积分路径I1是沿平行于虚时间轴的方向从ti到0,因此tr是一个常数.此时(34)式中的第1 项可以写为

积分路径I2是沿ti=0 的实时间轴,所以(34)式的第2 项写为

将(32)式—(36)式代入(31)式,可得鞍点方程变为

即在鞍点方程中考虑了势垒下库仑势的作用.

3 跃迁振幅

费曼路径积分思想是将波函数的贡献看作所有可能路径(携带与路径相关的作用量)的叠加,使用鞍点近似的SFA,CCSFA,TCSFA 与CQSFA均是以带作用量的轨迹来描述电子波函数.费曼认为可以将有限时间分成无限多趋近于零的小时间段,此时粒子在有限时间内传播可以看作粒子在每个时间段内传播的贡献总和.如图5(a)所示,粒子从A点到B点其中间存在一个双缝挡板时,在t0时刻粒子处于A点,t1时刻粒子到达挡板处,t2时刻粒子到达B点.如果t2-t1与t1-t0均无穷小,那么粒子从A点到达B点的概率为两条路径贡献总和.当挡板数与狭缝数增多时路径也同时对应增多(图5(b)),当挡板与狭缝无限多时可认为没有挡板存在,此时粒子从A点到B点的概率为无限多不同位置到达B点的路径贡献总和.当粒子从A点到达B点的时间为有限时,可以将时间分为很多个小时间段.推广到无数条狭缝且该时间段内挡板数也无数个,那么此时每条路径由折线变为了任意形状的曲线,如图5(c)所示,此时粒子从A点到B点的概率为空间中任意曲线路径的贡献总和.

图5 费曼路径积分思想示意图.A 与B 分别为粒子的初始点与末点,绿色虚线为粒子的可能路径 (a) 两个位置之间存在一个挡板双缝;(b) 两个位置间存在两个多缝挡板;(c) 两个位置存在无数个狭缝,此时粒子可以从A 点经历任意位置到达B 点Fig.5.Schematic diagram of Feynman’s path integral concept.A and B represent initial and final points of a particle,and the green dashed line represents the possible paths of particle: (a) There is a double-slit barrier between two positions;(b) there are multiple slit barriers between two positions;(c) there are infinite slits between two positions,and particle can reach point B from point A through any intermediate position.

从A点到B点的概率振幅来自于所有可能路径的贡献,每一条路径的贡献幅度一样,只有相位不同.而其相位则与经典作用量(S/ℏ)有关,ℏ 为普朗克常数,(S/ℏ)表明了对应于每条路径作用量S是量子化的.对宏观尺度,作用量子 ℏ 是个很小的量,因此对每条路径作用量S都 比 ℏ 大很多,对该路径的相邻路径而言,相位的变化非常巨大而使得这些路径贡献的几率振幅相互叠加抵消.只有当这条路径与其临近路线的相位变化不大时(对相位的变分为0)才不会相互抵消,即经典粒子的路径.可见路径积分方法结合最小作用量原理将量子现象过渡到了经典运动轨迹中,在经典物理与量子物理之间架起了一座桥梁.

跃迁振幅描述了电子从一个状态跃迁到另一个状态的概率,激光诱导的电离过程描述了电子在激光作用下从初态|ψ0(t)〉跃迁到连续态|ψp(t)〉的过程.此时束缚势与外加电场耦合下的哈密顿量可以写为

式中,W(t) 为 电场作用算符,V(r)为 势能算符,为动能算符.其对应的跃迁振幅为

其中,U(tf,ti) 为从时间ti到时间tf的时间演化算符.同时考虑外加电场与原子的束缚势,这很难得到TDSE 的解析解,所以将哈密顿量拆分为两项:

这里,H0(t) 为束缚电子 的哈密顿量,H(GV)(t) 为连续态自由电子的哈密顿量,对应的时间演化算符分别为U0(t,t′) 和U(GV)(t,t′).利用Dyson 方程[52],可将时间演化算符写为如下积分形式:

将(42)式代入(39)式,考虑正交性〈ψp(tf)|ψ0(ti)〉,第1 项的结果为0,那么可以得到跃迁振幅的积分形式:

将(43)式代入(44)式可将跃迁振幅分为2 项:

其中,等式右边第1 项为跃迁振幅的零阶项,描述了直接电子从束缚态跃迁到连续态的概率.在SFA 中,电子跃迁到连续态后被看作是自由电子不受到束缚势的影响.由于时间演化算子,又考虑到波函数的正交性,那么直接电子的跃迁振幅为

3.1 积分法计算跃迁振幅

从(46)式与(47)式可知直接电子与散射电子具有不同的跃迁振幅,光电子动量谱ω(p) 由跃迁振幅模的平方给出,通常不考虑电子返回再散射过程时,只需要计算跃迁振幅的零阶项.而且在不考虑库仑势的情况下,连续态电子被看作自由电子,其在电场中的振荡速度为p+A(t).对于给定的末动量p,考虑在长度规范下W(τ)=r·E(τ),同时将其与沃尔科夫平面波代入(46)式可得到电子末动量为p时的概率为

将(49)式代入(48)式可得

其中,F[F(r,τ)] 为F(r,τ) 的傅里叶变换,这样将每个时间下的跃迁振幅求和平方,便能得到光电子动量谱[53].

3.2 微分法计算跃迁振幅

由(50)式可知F(r,τ) 是含时变化的,所以无法得到其解析形式,因此在每个时间步长都需要数值计算快速傅里叶变换.另一种方法是从动量波函数出发,通过对其动量波函数求微分便能得到每一时刻跃迁振幅的解析表达式[54],ω(p) 将变成一重积分,令q=p+A(t),那么(46)式可以重写为

这里,ψ0(q) 是ψ0(r) 的傅里叶变换,表示自变量为q的动量空间波函数[55],其解析式为

对于其他量子态的动量空间波函数,可以将其对应的量子数代入(52)式得到其解析的波函数.实际计算时间的积分中,通常取电场开始时间0 与电场结束时间tf作为积分的上下限,将(53)式代入(51)式可得

3.3 利用鞍点近似方法计算跃迁振幅

跃迁振幅描述了电子从束缚态跃迁到连续态的概率,通过使用鞍点近似将其简化为许多轨迹的相干叠加,这样可以很清晰地分析不同时间窗口所出射电子的相干特性[56].作用量S(t) 作为一个指数,是关于时间t的高速振荡函数,可以利用鞍点近似方法来计算该时间积分[57],从而用电子轨道的形式来描述时空动力学.这不仅使计算更加简单,而且可以提供清晰的电子动力学过程物理图像.(46) 式描述了直接电离电子的跃迁振幅,对其使用鞍点近似可得

将所有鞍点的贡献求和便能计算出电子在渐进动量为p时的跃迁振幅,但是注意到其鞍点方程为

因此在满足鞍点条件下等式q2+2Ip=0 成立.那么根据(54)式可知,〈p+A(ts)|r·E(ts)|ψ0(τ)〉在鞍点处是一个奇点,以至于鞍点近似方法此时不再不适用.为了解决这个问题使鞍点等式成立,考虑将做变形,实际计算中取外加电场结束时间tf作为积分上限,电场开始时间0 为积分的下限.将符号计算展开为积分形式那么有

(57)式用到了[r·E(τ)+i∂/∂τ]e-i[p+A(τ)]·r=0以及动量波函数ψ0(q),其为空间波函数的傅里叶变换

对(57)式分部积分可得

对于零程势,基态空间波函数为

傅里叶变换形式 (动量波函数) 为

由(53)式可知,对于库仑势的动量波函数可以表示为

很显然,当选择零程势时,将波函数代入(59)式,其分母上的S′可以被消掉.但选择库仑势时,分母上的S′还保留着,这将导致奇异点的发生,将(62)式代入(59) 式得

其中

根据柯西积分定理,沿着实轴的积分 0 ≤t≤tf等于从0 到a+i∞的曲线积分,复数平面Cs的曲线积分,从b+i∞到tf曲线积分这三部分之和.这里a(b) 为连接曲线Cs的左端点(右端点)的实数.为了避免在ts发生奇点,曲线Cs通过点ts-iε,ε →0+.这时(64)式分裂成2 项:

对(65)式的第1 项使用分部积分可得

相对于第1 项,第2 项是关于S′的逆高阶项,所以可以忽略不计,因此(66)式中的主要贡献来自实轴上的2个点t=0与t=tf,发现该项可以与(63)式的第2 项抵消,所以跃迁振幅的贡献可以记为曲线Cs的积分.由于S′=0 被积函数是奇异的,分别将S与S′在鞍点处展开可得

将其代入 Ls可得

结合(63)式—(69)式,可以得到对于当束缚势为库仑势时,其跃迁振幅写为

4 库仑修正强场近似

众所周知,SFA 可以对复轨迹进行有效的解释,也称为量子轨道[58,59].复轨迹法的实质是: 由于不考虑库仑势,对于每一个最终光电子动量p可以找到一个或几个复电子轨迹r0(p,t) 满足经典的激光场中电子运动方程:

初始与边界条件有

(72)式前2 项为初始条件,表明电子处于原点(也就是原子的位置)其动能等于束缚能,第3 项为边界条件表明电子以动量p的状态打在探测器上.虽然这个轨道满足经典运动方程,但是其轨道为复数,说明电子从基态发生隧穿或多光子电离是量子效应.因为初始电子能量为负,那么其初始时间ts也是复数.当时间t=t0=Re[ts] 时,表明电子处于经典作用区域,此时隧穿出口r0(p,t=t0) 为一个实数.根据之前的初始条件可得

由于r0(p,t=ts) 为一个纯虚数,可得

根据之前的推导(70)式,SFA 电子的跃迁振幅为

另一个是由于轨迹修正r1导致的,记作

修正量r1由以下牛顿方程所决定:

其中,Zq为电荷量.如果选择轨迹r0(p,t),并且在实时间t≥t0演化(78)式,那么将得到不同的末动量v(t →+∞)≠p,这将无法对应一个特定的末动量p修正其跃迁振幅.但是,如果假定一个其他没有库仑的轨迹,在实时间演化(78)式其末动量恰好等于需要的动量.那么可以在作用量中用替代p,令=,库仑修r1的初始条件为.那么根据(76)式与(77)式可以计算出与这3个作用量.因此,修正后的电离振幅可以记作

5 基于轨迹的库仑修正强场近似

SFA 是一种广泛且成功地应用于处理强场电离过程的理论计算方法.在其最简单的形式中,只考虑所谓的“直接”电子,这些电子在电离之前被束缚在原子上,由于激光场的强度远大于库仑势的强度,电子在电离之后只在激光场的作用下运动,因此不存在散射电子.而TCSFA 是在SFA 的基础上对电子轨迹进行了修正,其不仅仅是体现在电子的运动方程,在作用量上也进行了修正.由于在轨迹中考虑了库仑势,那么电子不仅有直接电子,同时也存在散射电子[24].根据鞍点方程∂S(t)/∂t=,可知电子开始时间ts为复数,所以其电子轨迹可分为2 部分: 一部分为ts→Re[ts]=tr描述了电子在势垒下的过程;另一部分为tr →∞描述了电子在经典区域的过程.在势垒下电子的轨迹不受库仑势的影响,在经典区域电子的轨迹会受到库仑势的扰动,在整个过程中作用量都引入了库仑势的修正.虽然势垒下作用量考虑了库仑势的影响,但是鞍点方程并没有考虑该修正,所以TCSFA 的鞍点方程与SFA 的鞍点方程一致.鞍点方程的每个解,称为鞍点,对应着一个复电离时间.然而,对于大量的初始系综,求解这些鞍点方程是非常耗时的.为了克服这一困难,Xiao等[60]提出了一种时间采样的方法来解决这个问题.由鞍点方程可知通过时间上的采样从而求解对应的动量p比在动量上的采样求解时间容易很多.

通过给定的渐进动量求解鞍点方程得到电子开始时间ts,TCSFA 计算过程分为势垒下与经典区2 部分.电子在势垒下开始位置与电子到达经典区的初始位置分别记为rsub(ts) 与r(t0),由于势垒下电子的轨迹不受库仑势的影响,所以势垒下的运动方程为

但是势垒下的作用量考虑库仑势作了修正,记作

虽然经典运动过程中考虑了库仑势的扰动,但是其初始条件与SFA 一样,记作

其运动方程引入了库仑力导致其发生了畸变,所以vre(t →tf)≠p,运动方程由下式描述:

相应的经典运动中其作用量表示为

电子的电离概率等于跃迁振幅的平方,根据(75)式可以得到

由于Sre(tf)为实数,但是Ssub(t0) 为复数,所以电离概率可以重写为

其中电子的电离概率为

相位表示为

通过初始条件很容易计算出电子的电离概率w0,但是求解末态的动量与累积的作用量Sre(tf) 需要演化该动力学方程(83)式.这里使用了四阶龙格-库塔方法来求解该微分方程组[61].

电场在t=tf时关闭,自由电子的渐近动量p(∞)等于电场结束时的动量p(tf).但是在TCSFA 中,由于长程库仑势的作用,电子加速度不断变化,因而产生了p(∞)≠p(tf).若能量小于零,这部分电子被认为束缚到了里德伯态而未被电离.在没有电场的系统中,能量大于零的电子只受到中心库仑力的作用,可以看作经典二体问题,可以用开普勒轨道处理.事实上,电场结束时电子的动量p(tf) 与其位置r(tf) 唯一地确定了其在母离子库仑势下的运动轨迹,经典力学的双曲线运动标准公式可以解析求出电子渐近动量[62,63]:

这里,M=r(tf)×p(tf) 和A=p(tf)×M -r(tf)/r(tf)分别代表角动量守恒与龙格-楞次矢量.p(∞) 可由能量守恒定律得到:

最终,将大量随机轨道在末速度空间下相干叠加便能得到如图6 所示的动量图,可以看出考虑势垒下作用量的TCSFA 能定量地模拟TDSE 结果.

图6 pz -px平面内光电子动量分布图[24] (a) TDSE,(b) SFA,(c) TCSFA 不考虑势垒下作用量;(d) TCSFA 考虑势垒下作用量Fig.6.Logarithmically scaled photoelectron momentum distribution in pz -px plane[24]: (a) TDSE,(b) SFA and (c)TCSFA without sub-CC;(d) TCSFA with sub-CC.

6 库仑量子轨迹强场近似

第5 节提到的TCSFA 是通过给定的渐进动量求解鞍点方程得到电子的初始动量,然后通过引入库仑势的动力学方程演化电子的状态,最后统计电子的末态分布.CQSFA 则是选择给定的末动量通过3 个鞍点等式去求解电子的不同初态,这不同的初态包括4 类轨迹通过引入库仑势的动力学演化最后都会达到给定的末态从而相干叠加[25,26].

SFA 与CCSFA 中鞍点方程如(56)式所示只有一个等式,给定渐进动量p从而计算复数电离时间ts,这里的p在强场近似中对应末动量.但是在CQSFA 中,不仅仅需要找到ts,同时需要根据电子末 动量p(tf) 来求得电子初始位置r(tr) 与 初始动量p(tr).所以其鞍点方程必须同时满足3 个等式:

(92)式描述了隧穿过程能量守恒,(93)式与(94)式描述了电子在连续态的动力学过程τ ∈(tr,Tp).对于简单的库仑势V(r)=-C/|r|,由(93)式可以得到

将(95)式代入(92)式可得

其中p(ts) 为势垒下的渐进动量,通常近似值是固定 的,即p(t1)=p(t2),t1∈[ts,tr],t2∈[ts,tr].那么就有(ts)→0,将其代入(96)式得

设电场矢势为Az(t)=A0cos(ωt),(97)式有两个鞍点解,这里记作

其中p0//为平行于电场方向电子的初始速度,p0⊥为垂直于电场方向电子的初始速度.1,2,3,4 分别代表4 类不用初始条件的轨道,其中 (1,4) 与 (2,3)时间表达式一样但是由于其初始速度不同导致时间也是不同的.将隧穿位置作为初始位置与末动量作为限制条件,求解(93)式与(94)式得到电子初始动量.其具体做法是求解一个反问题,运用迭代的方法不断地增加库仑耦合的作用.首先假设库仑耦合作用为0,即C=0,用强场近似的解作为初始解,再令C=0.1 代入之前的解,显然在动力学方程中引入的库仑耦合作用发生改变之后,末动量的解不等于之前的限制条件,这时需要根据限制条件来修正之前的解从而改变初始动量.然后不断增加库仑耦合作用,直到C=1 时库仑耦合作用完全引入之前的鞍点方程,这样就得到了4 类初始条件不同但是末动量一致的轨道.这种方法没有根据最终动量明确地参数化初始动量,但使每个轨道的初始动量能够计算出任何给定的最终动量.使用鞍点近似,由(20)式可得跃迁振幅为

其中下标s 代表鞍点,ts,ps,rs是通过求解(92)式—(97)式得到,进而根据空间积分或者傅里叶变换求解〈p+A(ts)|r·E(ts)|Ψ0〉.∂ps(tf)/∂rs(ts) 为 稳定因子,前项因子为

相位分为两项:

其中等式右边第1 项与第2 项分别为延时间虚轴与时间实轴累计的作用量.沿虚轴时的轨迹没有受库仑势的影响,作用量可表示为

其中

沿实轴的作用量表示为

将(95)式代入(104)式可得

其中

最后,将相同末动量的4 类轨道相干叠加可得到光电子角度分布(图7).由图7 可以看到,CQSFA 也能定量地复制TDSE 的结果.并且计算中只存在4 类轨迹,在解析物理图像时能更加有效地辨识背后的产生机制.

图7 氢原子二维光电子角度分布[26] (a) CQSFA;(b) SFA;(c) TDSEFig.7.Two-dimensional photoelectron angular distributions of hydrogen atom[26]: (a) CQSFA;(b) SFA;(c) TDSE.

7 结论与展望

费曼路径积分方法提供了一种量子轨迹的强场动力学计算方法,使得人们可以从经典的视角去研究量子效应,为强场物理在研究微观世界粒子动力学过程取得了突破性的进展.本文介绍了使用遗传算法与牛顿迭代法优化复平面鞍点方程的计算模型,这两种方法能够有效减少计算所消耗的时间.详细推导了几种费曼路径积分强场动力学计算方法,包括SFA,CCSFA,TCSFA 与CQSFA.由于SFA 忽略了库仑势的作用,不能在定量上与实验结果相符合.CCSFA 在作用量里面考虑了库仑势的影响,同时将轨迹的修正以作用量的形式考虑在内.TCSFA 将轨迹的修正直接考虑在运动方程中,同时作用量也由每一时刻能量的积分得到.这2 种方法都需要大量的计算轨道,CQSFA 则是将每个末动量下分为4 类轨道,有效地减少了计算量同时保证了计算的质量.相比前两种方法,该方法虽然简化了计算,但是鞍点方程却更为复杂,不易于寻找到合适的鞍点,通常需要不断迭代才能寻找到合适的鞍点.由于这3 种方法都引入了库仑势的作用,其都能与实验结果做定量比较.虽然现在费曼路径积分强场动力学计算方法已经被广泛应用,但是其局限性很明显: 一是多原子、多电子等复杂波函数很难解析得到;二是轨道如何从经典轨迹解释清楚量子效应.如何将费曼路径积分强场动力学计算方法推广至更复杂的系统,对量子效应提出更好的解释模型,需要在此基础上发展更加有效的理论方法.