苜蓿茎秆压扁过程力学特性仿真与试验

王林，侯传凯，张克平

（730070 甘肃省 兰州市 甘肃农业大学 机电工程学院）

0 引言

苜蓿作为国家的重要战略资源，是奶牛养殖过程中优质的蛋白质来源[1]。随着苜蓿种植面积的不断增加，苜蓿收获及加工机械的需求量也越来越大[2]，其中割草压扁机是一种用来收获优质饲草的机具，具有收割、压扁调制等功能，对提高饲草的经济效益具有重要作用[3]。

近年来，离散元法及其仿真软件EDEM 在农业机械领域得到了广泛应用，农作物茎秆作为收获机械作业中的重要物料，其离散元仿真过程的参数设置将直接影响分析结果的准确度，因此有关茎秆参数标定的研究也不断增多。廖宜涛等[4]通过堆积角和响应面试验标定了油菜茎秆离散元接触和粘结参数；张李娴[5]通过万能试验机对玉米茎秆外表皮与内穰作力学特性试验，得出粘结模型及玉米茎秆表皮弹性模量；侯杰等[6]基于HBP 仿真模型通过堆积角和三点弯曲试验，对水稻茎秆接触参数和粘结参数进行离散元仿真标定；马彦华等[7]以休止角为目标值，对苜蓿茎秆压缩过程中离散元接触参数进行标定。

建立苜蓿茎秆离散元模型，模拟其在机械化收割及压扁调制过程中的运动和受力规律，可为相关机具的设计和优化提供理论依据。目前关于苜蓿茎秆的研究多集中在物理试验方面，对于离散元仿真分析中涉及的相关参数研究较少。本文采用离散元Hertz-Mindlin with bonding 颗粒接触方法建立苜蓿空心茎秆模型，通过力学试验测定苜蓿茎秆相关特性参数，再结合力学试验与虚拟仿真对比校正离散元模型，为苜蓿茎秆在收割、压扁等环节离散元建模及仿真研究提供参数依据。

1 苜蓿茎秆离散元模型建立

1.1 接触模型的选择

离散元法（Discrete Element Method，DEM）颗粒接触模型的选择是仿真过程的重要环节[8]，Bonding 接触模型是Potyondy 和Cundall 开发用以模拟物料破碎断裂等问题[9]，在研究苜蓿茎秆的接触模型时可选用该模型。如图1 所示，模型可使相邻两颗粒在接触点发生平行粘结，该粘结可以承受切向和法向位移，直到达到最大的法向和切向剪切应力时，粘结键断裂，颗粒分开发生破碎，此后，颗粒作为硬球相互作用。Bond 键作用效果相当于分布在球形基础颗粒截面上的一组弹簧，通过接触点处的力Fi与力矩Mi描述材料力学特性，在外力作用下发生拉伸、压缩、扭转等形变，符合苜蓿茎秆等黏弹性物料的压缩分析。

图1 Bonding 接触模型Fig.1 Bonding contact model

粘结之后，颗粒上的力（Fn，t）与力矩（Tn，t）的初始值设置为0，并在每个时间步通过式（1）逐步调整。

式中：δFn——法向粘结力，N；δFt——切向粘结力，N；Sn，St——单位面积法向、切向刚度，N/m；Vn、Vt——切向和法向速度，m/s；δt——仿真时间步长，s；Wn、Wt——法向和切向角速度，rad/s；δMn、δMt——法向、切向力矩，N·m；J——惯性矩，m4；A——接触区域面积，m2。

当力或力矩超过某个预定义的值时，粘结键发生断裂，法向及切向剪切力计算公式为

式中：σmax、τmax——法向、切向临界应力，Pa；Rb——粘结键半径，mm。

由于粘结力或力矩是额外加到标准Hertz-Middlin 力中的，此模型在颗粒无实际接触时就起作用，故接触半径应设置成大于实际半径。

1.2 苜蓿茎秆离散元模型构建

为建立茎秆的离散元模型，选取收获期苜蓿植株20 株，在中部截取长20 mm 茎秆进行几何尺寸测定，测得苜蓿茎秆的平均外径为3.62 mm，壁厚为0.76 mm。采用SolidWorks 建立空心茎秆的几何模型，将模型的“stl”文件导入EDEM 分析软件，再通过Bond 键粘结颗粒建立茎秆离散元模型，如图2 所示。

图2 苜蓿茎秆及离散元模型Fig.2 Alfalfa stalk and discrete element model

在构建茎秆模型时，填充颗粒直径越小仿真时间越长，构成的粘结键数目就越多[10]。上述模型的球形颗粒半径为0.36 mm，颗粒数量为429 个，由1 244 个Bond 键构成。建模完成后，可在后处理中导出每个颗粒的坐标信息方便后续仿真分析。

2 离散元模型参数确定

马彦华等[7]的研究标定了压缩仿真中茎秆的接触参数，王昊毅[11]在EDEM 中对苜蓿茎秆仿真参数进行了标定，相关数据可用于本研究中苜蓿茎秆离散元参数设定。但针对苜蓿茎秆离散元模型bond 键的粘结参数尚未有研究，需要通过力学特性试验确定相关参数。

2.1 苜蓿茎秆力学特性参数测定

不同品种、生长环境和成熟度造成苜蓿茎秆内部结构存在差异。本研究选取试验样本为兰州新区收获期苜蓿茎秆，挑选无病虫害、无机械损伤的通直主茎秆，去掉叶片后,采用游标卡尺测量茎秆外表皮厚度与宽度，选取直径为3.62±0.03 mm、壁厚为0.76±0.03 mm 的茎秆截成长度为20 mm 的无节试样[12]。

用烘干法对茎秆进行含水率测定。使用BSA224S 型电子天平测量记录初始质量，之后放入温度为105 ℃的干燥箱中烘干，当测得时隔1 h 的两次质量差小于0.1 g 时，取其平均数值记录，苜蓿茎秆含水率M计算公式为

式中：m1、m2——干燥前、后质量，g。

为减小数据误差，采用3 组平行对照试验，取平均值后得茎秆含水率为74.7%。

选用SMS 公司生产的型号为TA.XT plus 的超技质构仪进行力学特性试验，最大载荷为300 N,精度为0.1 g,完成苜蓿茎秆的压缩、剪切试验，依据试验数据标定相关参数。

苜蓿茎秆在压缩过程中，主要产生径向变形与压力，轴向变形与压力较小，因此进行径向压缩试验[13-14]。将处理好的试样端面进行平整处理后，放在质构仪压缩平台的中心位置，压缩探头选用P/36R,加载速度设置为2 mm/min,每次试验完成后重新校正高度，取5 次重复试验的平均值，径向压缩试验结果见表1，可得最大径向压力的平均值为113.6 N,抗压强度的平均值为1.17 MPa。

表1 苜蓿茎秆径向压缩试验Tab.1 Radial compression test of alfalfa stalk

剪切试验中，由于苜蓿茎秆外表皮弧度会影响试验结果，因此处理样品时将其均分为更小份数，选取较为平整部分进行剪切试验[15]。将苜蓿茎秆试样放在质构仪的试验台，选用A/MORS 用剪切探头，考虑到较小加载速度下的变形更接近真实应变，加载速度设置为10 mm/min，每次试验前进行力与高度的校正，取5 次重复试验的平均值，试验结果见表2，得到最大载荷的平均值为55.2 N，抗压强度的平均值为6.92 MPa。

表2 苜蓿茎秆剪切试验Tab.2 Shear test of alfalfa stalk

2.2 Bond 键粘结参数计算

根据Bonding 粘结模型理论，颗粒之间产生粘结键的主要参数有法向刚度系数Kn、切向刚度系数Ks、法向临界应力σ、切向临界应力τ和粘结半径Rb。

式中，va、vb——颗粒的泊松比；ra、rb——颗粒半径，mm；Ea、Eb——颗粒弹性模量，MPa；F——临界压力，N；a——接触面椭圆的半长轴长，mm；l——茎秆压缩试样长度，mm；A——剪切处横截面积，mm2；Q——剪切载荷，N；D——苜蓿茎秆直径，mm；t——苜蓿茎秆壁厚，mm。

取苜蓿茎秆的密度为256 kg/m3，弹性模量为788.826 MPa，泊松比为0.3。因颗粒为同一材质，所以颗粒a、b各参数相等，再由力学特性试验得到最大临界载荷为113.6 N，剪切载荷为55.2 N，受力面积为S=6.82 mm2，代入式（4），可得Kn=1.97e+08 N/m3,Ks=1.319e+08 N/m3，σ=1.17e+06 Pa,τ=6.916e+06 Pa,取粘结半径Rb=0.54 mm。

3 离散元模型参数验证

3.1 压缩仿真试验

采用离散元软件 EDEM 建立与实际试验一致的压缩和剪切仿真模拟试验，为了确保模拟结果尽可能接近实际破碎效果，需要在模拟过程中反复调整粘结模型的相关参数，根据破坏后的表现特征与物理试验对比进行粘结参数的确定[16]。为趋近真实，仿真中的三维模型参照压缩、剪切试验中所用仪器的大小，将SolidWorks 中建立的模型以.stl 格式导入EDEM。

当苜蓿茎秆进行压缩时，根据试样特性曲线图，压缩可分为3 个阶段:前期为茎秆的线性变形阶段，此时茎秆被压缩变形；中期为压扁阶段，由于苜蓿茎秆中部为空心，故此阶段主要进行茎秆的压扁；后期为压实阶段。从图3（a）—图3（c）可以看出,在整个过程中，端面呈现出由圆形到椭圆的变化；从图3（d）—图3（f）的仿真试验可见，同样出现类似图3（a）—图3（c）的压扁现象。对比径向力学试验与仿真试验结果可得，相对误差在7%～11%，证明所建苜蓿空心茎秆分布模型可靠，试验结果如图4 所示。

图3 苜蓿茎秆径向压缩试验与仿真试验对比Fig.3 Comparison between radial compression test and simulation test of alfalfa stalk

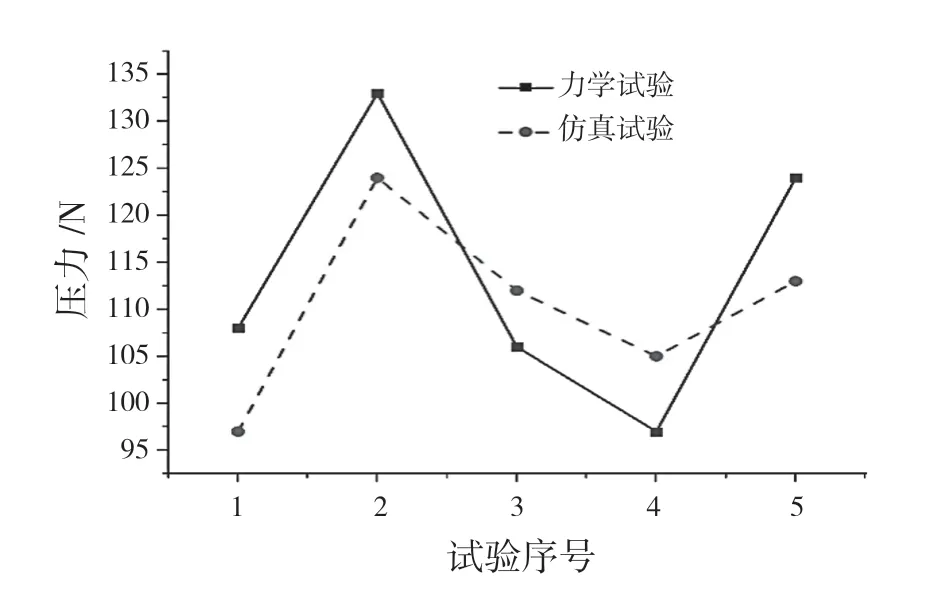
图4 苜蓿茎秆径向压缩力学试验与仿真试验结果Fig.4 Experimental and simulation results of radial compression mechanics of alfalfa stalk

3.2 剪切仿真试验

苜蓿茎秆在径向剪切试验中，如图5（a）所示，表皮发生破坏被切穿，刀尖由厚壁机械组织刺穿至网状维管束组织；仿真试验对苜蓿茎秆进行模拟，由图5（b）可见，剪切处的粘结键发生断裂，同时切宽厚度、剪切后茎秆的形态与物理试验中的破坏行为一致。

图5 苜蓿茎秆径向剪切试验与仿真试验对比Fig.5 Comparison between radial shear test and simulation test of alfalfa stalk

苜蓿茎秆在剪切过程中经历了3 个阶段：前期为拉伸阶段，茎秆随位移的增加载荷也逐渐增大，发生弹性变形；中期为拉伸-剪切阶段，当茎秆外部发生塑性变形时，持续加大载荷，内外应力逐步趋于一致，此时处于塑性变形阶段，在达到极限应力值后，茎秆发生断裂；后期为纯剪切阶段。如图6所示，对比剪切试验与仿真试验结果可得，相对误差在8%～15%，证明所建苜蓿空心茎秆分布模型可靠。

图6 苜蓿茎秆剪切力学试验与仿真试验结果Fig.6 Shear mechanics test and simulation test results of alfalfa stalk

上述仿真试验中苜蓿茎秆粘结模型参数所表现出的力学形态与在物理试验中茎秆的实际情况接近，最终确定Bonding 粘结模型参数如表3 所示。

表3 Bonding 粘结模型参数Tab.3 Bonding model parameters

4 压扁过程数值模拟

4.1 试验条件

为探究苜蓿茎秆在压扁过程中的变化情况，在EDEM 中设置苜蓿茎秆的粘结模型参数进行仿真计算时，采用Particle Replacement.Dll API 插件将大颗粒替换成7 996 个小颗粒组成苜蓿空心茎秆离散元模型，为使模型牢固粘结，替换后的小颗粒添加bond 键。为便于观察苜蓿茎秆离散元模型的压扁效果和减少仿真计算时间，在仿真过程中生成4 个茎秆离散元模型，再将人字形压扁辊的三维模型图以.step 格式导入EDEM，再与真实试验相同的喂入量、辊间间隙、压扁辊转速条件下进行虚拟仿真试验，如图7 所示。

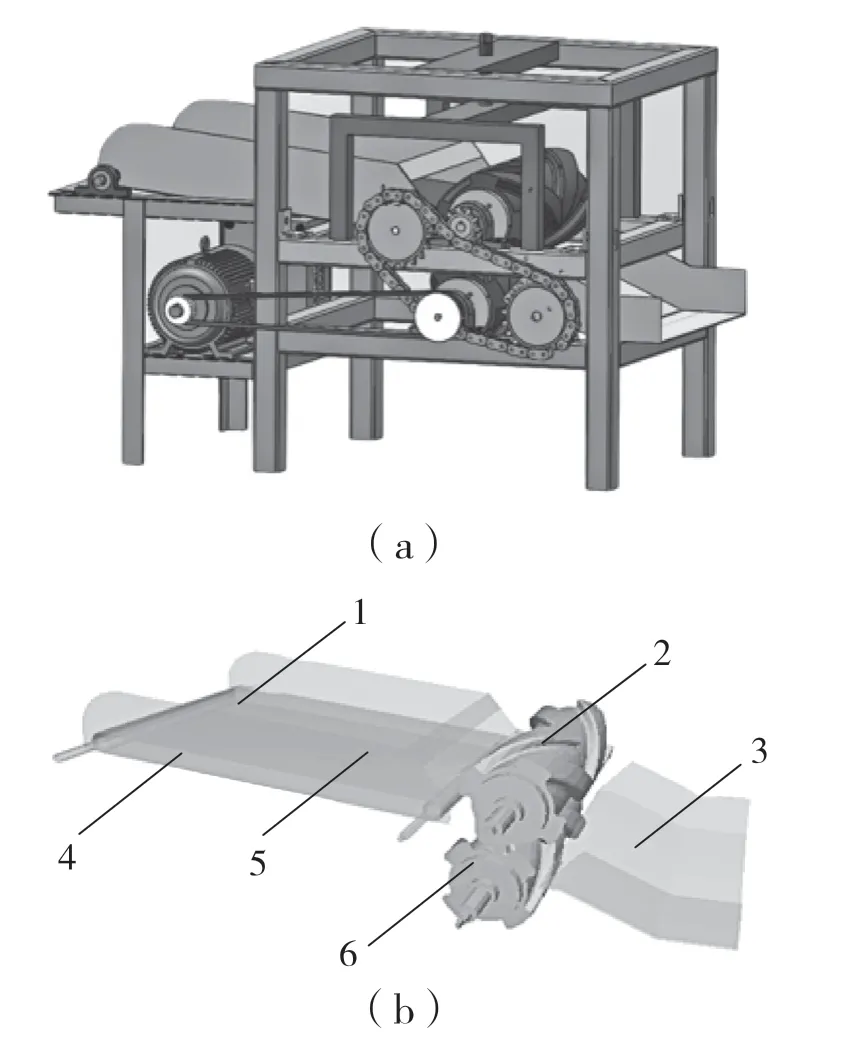
图7 压扁过程仿真图Fig.7 Simulation diagram of flattening process

4.2 试验结果分析

根据EDEM 后处理分析可知，每个茎秆模型大致由27 481 个粘结键组成，又因模型是由7 996个球形小颗粒构成，故平均每个颗粒旁有3.43 个粘结键，证明模型是充分粘结的。

图8 是模拟试验过程中苜蓿茎秆粘结键断裂数量变化示意图。在0.61～0.62 s 时，茎秆从输送皮带落下，受到吸附力的作用被卷入压扁辊表面，此时茎秆处于完整状态，故粘结键暂时没有发生变化；在0.62～0.65 s 时，上下压扁辊对茎秆进行压扁，此时茎秆受到的剪切力增强，故粘结键的断裂数量逐渐上升；在0.65～0.66 s 时，茎秆完全通过压扁间隙，不再受到剪切力的作用，此时粘结键数量趋于稳定。

图8 粘结键断裂数量变化过程Fig.8 Process of broken bond number variation

在整个压扁过程中，苜蓿茎秆受到压扁、摩擦的作用导致粘结键发生断裂，压扁仿真过程如图9 所示。图9（a）为苜蓿茎秆进入压扁辊前，上下压扁辊之间的高速运动可在两辊入口处形成一定的压力差，此时茎秆受压最小；图9（b）时茎秆刚进入两辊间，此时茎秆受压初步增大；图9（c）中左半截茎秆处于压扁状态，可明显看出，受压部分比未压部分受到的压力要大，此时茎秆受压再次增大；当茎秆完全处于压扁辊之间时，如图9（d）、图9（e）所示，由于既受到辊压力又受到摩擦力的作用，茎秆产生变形压扁，受压仍处于增加阶段；图9（f）为茎秆离开两辊间，此时压扁完成将要输出，可发现茎秆受压减小，变形部分恢复，但受压程度仍大于进入两压扁辊前，之后在惯性力作用下被输送至接料处，完成整个压扁过程。

图9 压扁过程中茎秆受压仿真图Fig.9 Simulation diagram of stalk compression in flattening process

5 结论

（1）采用离散元分析软件建立了苜蓿茎秆的离散元模型，以2 mm/min 和10 mm/min 为加载速度进行茎秆压缩和剪切试验时，分别得到苜蓿茎秆的最大径向力113.6 N 和最大载荷55.2 N；

（2）结合力学特性试验对苜蓿茎秆进行颗粒粘结模型及参数校核，获得了含水率为 74.7%时茎秆的粘结参数，法向刚度系数为3.45e+08 N/m3、切向刚度系数为3.15e+08 N/m3、临界法向应力为2.32e+06 Pa、临界切向应力为7.16e+06 Pa,、粘结半径为0.54 mm；

（3）对苜蓿茎秆离散元模型的压扁过程进行了仿真试验，与力学试验对比，证明所建苜蓿空心茎秆分布模型的可靠性。苜蓿茎秆模型的粘结键断裂数量随着剪切力的增大而增大，最终趋于稳定。茎秆所受压力随压扁的进行先增大后减小。

研究结果可为苜蓿茎秆离散元仿真研究和相关机具的设计优化提供参考依据。