车辆半车半主动悬挂系统PSO-Fuzzy 混合控制策略

赵羊羊，雒琦，韩威，牟晓斌，田斌，马圣杰，吴向峰

（1.730070 甘肃省 兰州市 甘肃农业大学 机电工程学院；2.714000 陕西省 渭南市 陕西铁路工程职业技术学院）

0 引言

高速车辆行驶时由于轨道不平顺会使车辆的2个转向架产生不规则振动，进而使车身发生垂直和点头运动，对车辆的操作稳定性和乘坐舒适性有很大影响。车辆悬挂系统可在一定程度上减弱振动，最早是利用悬挂弹簧和阻尼器的被动能力发挥缓冲作用，随着控制技术的智能化发展，车辆半主动悬挂系统被引入车辆振动控制，其可根据轨道不平顺的实时反馈和车辆响应特性，通过控制理论对磁流变阻尼器进行实时调节，从而提升减振性能[1]。

为了使车辆半主动悬挂系统性能更优，许多控制策略被应用到半主动悬挂的控制中，如经典的PID 控制[2]、神经网络控制[3]、模糊控制[4]以及不同控制策略结合的模糊PID 控制[5]、模糊神经网络控制[6]等。各种控制策略虽能有效对阻尼器进行控制，但控制器参数还不能精确设置。鉴于此，学者利用遗传优化[7]、粒子群优化[8-10]等算法对上述控制器进行优化，以期得到精确的控制器参数，使半主动悬挂系统得到更精确的控制。

本文采用粒子群优化算法的全局随机搜索能力对模糊控制器的参数进行优化，在一群随机粒子中经过无数次迭代之后得到最优解。根据车辆半车半主动悬挂系统力学原理，建立半车6 自由度悬挂系统模型，以此为控制对象，设计基于粒子群优化的半车半主动悬挂系统模糊控制策略，对比分析在普通Fuzzy 和PSO-Fuzzy 控制下半主动悬挂系统控制效果的优劣。

1 建立模型

1.1 车辆半车半主动悬挂系统模型

将车辆半车结构进行简化，简化后的模型具有6 个自由度，分别是车身和前后转向架的垂直、点头运动，建立如图1 所示的高速车辆半车半主动悬挂系统动力学模型。

图1 车辆半车半主动悬挂系统动力学模型Fig.1 Dynamic model of semi-active suspension system of semi-complete vehicle

6 自由度半车半主动悬挂系统的运动微分方程如式（1），参数含义如表1 所示。

表1 参数含义Tab.1 Parameter meaning

1.2 轨道不平顺模型

随机轨道不平顺模型由轨道等级、车辆运行速度与白噪声共同推导而来，其中的轨道等级选择第6 级轨道。轨道功率谱密度为

则轨道谱的时间频率为

高斯白噪声信号为

将式（7）代入式（6），得到传递函数

将式（9）反拉普拉斯变换，可将轨面垂直加速度响应表达为

2 设计PSO 优化Fuzzy 控制方案

2.1 Fuzzy 控制策略

因前、后二系悬挂中分别需要对各自磁流变阻尼器进行Fuzzy 控制，所以选择控制变量时，以车身与各自悬挂连接部位的垂直振动加速度和各自构架与车身的速度相差值为2 个输入变量，以各自磁流变阻尼器电流i为输出变量。

输入变量模糊子集表示为

输出变量模糊子集表示为

隶属度函数为

输入、输出变量范围：垂直加速度∈[-amax，amax]，速度差∈[-bmax，bmax]，电流i∈[0,imax]。

论 域：A={-a,-a+1,…,0,…,a-1,a}，B={-b,-b+1,…,0,…,b-1,b}，I={0,…,i-1,i}，分别取a=6、b=6、i=2。由于amax≠a，bmax≠b，imax≠i，则得到量化、比例因子为

即：Ka=6.667，Kv=150，Ki=1。

制定如表2 所示的控制规则。

表2 控制规则表Tab.2 Control rules

2.2 PSO-Fuzzy 控制策略

本文利用PSO 算法对Fuzzy 控制器的量化因子Ka、Kv及比例因子Ki进行优化，如图2 所示。

图2 PSO-Fuzzy 优化示意图Fig.2 Schematic diagram of PSO-Fuzzy optimization

PSO-Fuzzy 优化性能的评估指标确定为以车身垂直加速度均方根值为目标函数：

采样周期T=T2-T1，T1＜T＜T2。J值越小，车辆垂直振动越小，即PSO 对Fuzzy 的优化越佳。因PSO 在寻优过程中搜索范围较大，为防止盲目无效搜索，将车身垂直加速度进行限制作为约束条件：

PSO 对Fuzzy 控制器的Ka、Kv及Ki寻优流程如图3 所示。

图3 PSO-Fuzzy 优化控制流程图Fig.3 Flow chart of PSO-Fuzzy optimization control

在MATLAB/Simulink 中用仿真函数sim 编写PSO 算法程序，实现目标函数：

在PSO 优化时，将最优的粒子（Ka、Kv、Ki）提供给Fuzzy 控制器，然后将所得适应值返回给PSO 进行判断，若满足终止目标条件或迭代完成，则优化结束，将此时的Ka、Kv及Ki作为Fuzzy 控制器的最优参数。

3 MATLAB/Simulink 仿真分析

3.1 轨道模块图

根据式（10）搭建如图4 所示的轨道不平顺模块图。仿真得到如图5 所示的轨道位移响应图。

图4 轨道不平顺模块图Fig.4 Module diagram of track irregularity

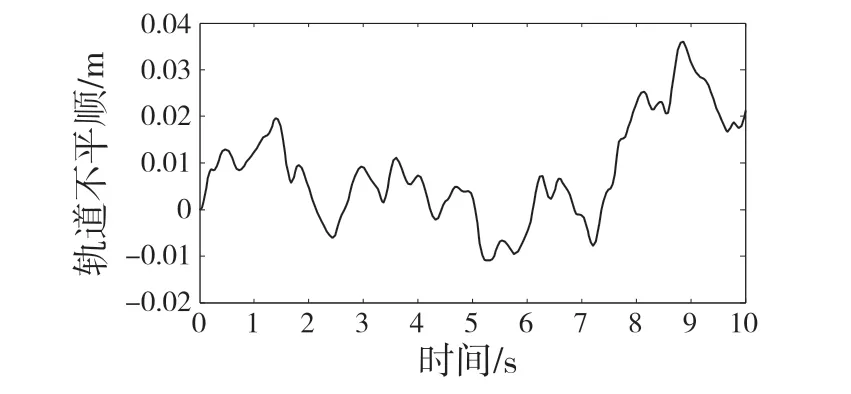
图5 轨道位移响应图Fig.5 Response diagram of track displacement

3.2 半车半主动悬挂系统Fuzzy 模块图

根据式（1）搭建如图6 所示的基于Fuzzy 的半车半主动悬挂系统模块图。

图6 半车半主动悬挂系统Fuzzy 模块图Fig.6 Fuzzy module diagram of semi-active suspension system of semi-complete vehicle

根据表1 中参数选取高速车辆半车半主动悬挂系统的仿真参数，如表3 所示。

表3 高速车辆悬挂系统参数值Tab.3 Parameter values of high-speed vehicle suspension system

3.3 半车半主动悬挂系统PSO-Fuzzy 模块图

在半车半主动悬挂系统Fuzzy 模块图的基础上添加PSO 寻优模块，以车身垂直加速度作为最终优化的性能指标，建立如图7 所示的半车半主动悬挂系统PSO-Fuzzy 模块图。

图7 半车半主动悬挂系统PSO-Fuzzy 模块图Fig.7 PSO-Fuzzy module diagram of semi-active suspension system of semi-complete vehicle

PSO 优化算法模块的仿真参数设置如表4 所示。

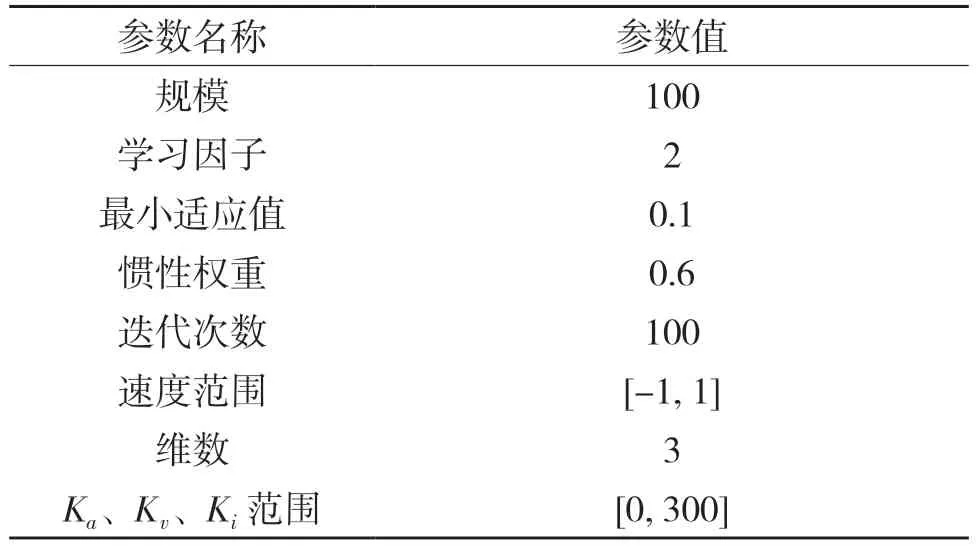
表4 粒子群优化算法参数Tab.4 Parameters of PSO algorithm

3.4 仿真分析

为了验证PSO-Fuzzy 控制的优化效果，在相同轨道激励和运行速度下，对Fuzzy 和PSO-Fuzzy分别控制下的半车半主动悬挂系统进行仿真分析，在寻求最优的量化因子Ka、Kv及比例因子Ki的基础上，对比分析车身垂直加速度、垂直位移及点头转角3 项仿真结果变化图和车身垂直加速度均方根值（J值）指标的数据变化关系。

以图4 轨道不平顺作为车轮输入激励，车辆运行速度v=250 km/h，将表3、表4 参数设置到图6、图7 模块中。采用PSO 寻优后，最优适应值曲线如图8 所示。

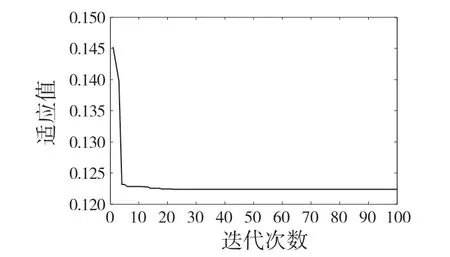
图8 PSO 算法适应值曲线Fig.8 Adaptation value curve of PSO algorithm

在考虑高速车辆垂直和点头运动情况下，图9、图10 和图11 为半车半主动悬挂系统分别在Fuzzy和PSO-Fuzzy 控制时车身垂直加速度、垂直位移及点头转角3 项数据的仿真对比图。

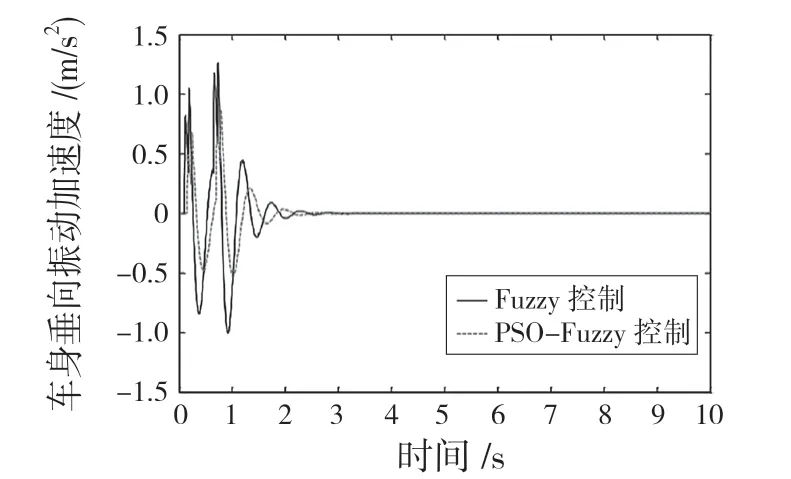
图9 车身垂直加速度对比Fig.9 Comparison of vertical acceleration of vehicle body

图10 车身垂直位移对比Fig.10 Comparison of vertical displacement of vehicle body

图11 车身点头运动转角对比Fig.11 Comparison of vehicle body nodding motion angle

Fuzzy 与PSO-Fuzzy 两种控制策略下的Ka、Kv、Ki参数值、J值以及车身垂直振动加速度峰值的数据对比如表5 所示。

表5 Fuzzy 与PSO-Fuzzy 控制对比Tab.5 Comparison of Fuzzy and PSO-Fuzzy control

由图9—图11 和表5 可知，相比Fuzzy 控制，经PSO-Fuzzy 优化后得到了更精确的控制器量化因子Ka、Kv及比例因子Ki值，车身垂直加速度均方根值J值变小，数值由0.140 减小到0.124，减小了11.429%；车身垂直加速度峰值由1.295 m/s2减小到0.883 m/s2，降低了31.815%；车身垂直位移和点头转角振幅峰值也相应减小，系统更早地达到稳定状态。

4 结论

（1）建立高速车辆半车半主动悬挂系统模型，并通过白噪声信号推导出轨面垂直加速度响应表达式；

（2）针对普通Fuzzy 控制器中的量化因子Ka、Kv及比例因子Ki受专家经验限制，本文提出了运用PSO 算法来优化Fuzzy 控制器的量化、比例因子，分别设计了Fuzzy 控制器和PSO-Fuzzy控制器；

（3）在MATLAB/Simulink 仿真平台分别搭建轨道激励模块图和针对半车半主动悬挂系统的Fuzzy 控制模块图与PSO-Fuzzy 控制模块图。仿真结果发现，相对于普通Fuzzy 控制器，PSO-Fuzzy能够使车辆半车半主动悬挂系统在随机轨道激励作用下车身垂直加速度、垂直位移及点头转角得到显著降低。优化方案有效提高了半主动悬挂系统的减振性能。