基于3D关联规则深度学习的异构遥感数据检测
覃伟荣,劳燕玲
(北部湾大学资源与环境学院,广西 钦州 535011)
1 引言
随着遥感卫星技术的不断发展,一方面增加了遥感卫星传感器以及遥感数据类型,另一方面导致数据量急剧增加,对遥感数据的管理以及存储等带来了巨大的挑战[1,2]。同时,由于遥感数据自身具有时空等多维度特征,越来越多的遥感应用开始关注遥感数据集的时间分析和管理,在现有微型数据中心环境下,数据的获取以及分析存在效率低下等问题,所以对异构遥感数据有效检测成为当前研究的关键问题。
相关专家对此进行了大量研究,并给出了一些较好的研究成果,李新鹏等人[3]通过历史数据组建多个子森林异常检测器,同时组建森林异常检测器,将数据输入到检测器中完成数据异常检测。胡姣姣等人[4]通过抽样法对不平衡时间数据实施预处理,将经过处理后的时间序列数据转换为尺度和时间一致的片段,同时将数据输入到卷积神经网络模型中完成异常检测。闫媞锦等人[5]通过含有可训练迟滞项的门控循环单元对缺失和非规则采样的时序数据实施建模,采用极值论中的自适应阈值确定合适阈值,最终达到异常检测的目的。在以上几种方法的基础上,提出一种基于3D关联规则深度学习的异构遥感数据检测方法。经实验测试结果证明,所提方法可以有效提升检测结果,降低检测时间。
2 异构遥感数据检测方法
2.1 遥感数据去噪
小波变换可以将遥感数据分解为低频和高频信息,为了更好地保护遥感数据的细节特征,提出一种基于双树复小波的四阶偏微分方程数据去噪模型[6,7],模型中两个关键的去噪部分为:
1)对于含有噪声的原始遥感数据,需要实施二维双树复小波分解,分解出包含大量噪声的高低频子带,经过去噪处理的高低频子带采用双树复小波重构,最终得到去噪后的遥感数据。
2)对复高频子带的实部和虚部分别使用四阶偏微分模型完成去噪。
在去噪模型中,通过Q-Shift滤波组对含有噪声的遥感数据实施一维双树复小波多尺度分解,分解后灰度梯度比较低的信息即为背景信息,而分解后含有大量噪声的高频子带则为噪声或者边缘信息。
双树复小波分解的详细操作步骤如图1所示。
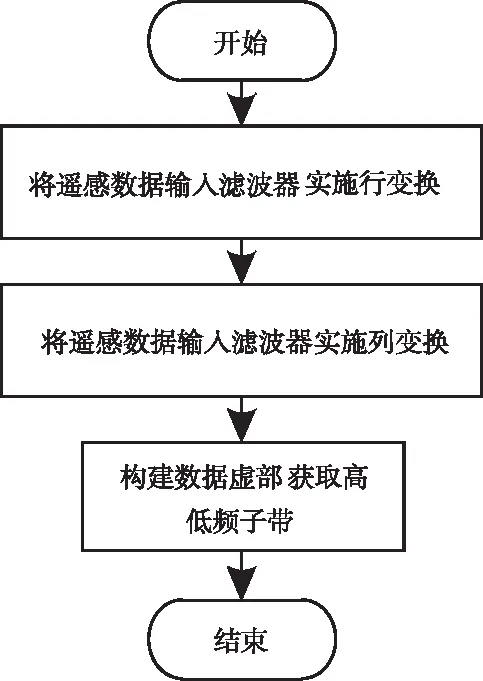
图1 双树复小波分解流程图
偏微方程的求解思路主要采用有限差分法完成数值计算,有限差分法的基本操作思路为:
通过一定的步长根据时间和空间完成格网划分,同时将连续的偏微分方程采用差分近似代替导数的方式划分为多个代数方程,同时求解代数方程组,获取各个网格节点的取值。
有限差分法的详细操作步骤如下所示:
1)将时间和空间区域离散化处理;
2)将各个网格上的导数通过像素灰度值计算,将计算得到的差分作为近似替换;
3)根据推导出的迭代公式,设定最佳迭代次数,同时采用梯度下降法求解[8,9],其中梯度下降流可以表示为式(1)的形式
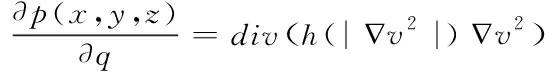
(1)
式中,p(x,y,z)代表欧拉方程;q代表时间变量;h代表最佳迭代次数。
为了对方程离散化处理,主要借助有限差分法实现。在遥感数据中心点,可以获取对应的二阶差分∇h(i,j),具体的计算式为
∇h(i,j)=(vxx)i,j+(vyy)i,j
(2)
其中

(3)
式中,(vxx)i,j和(vyy)i,j代表二阶差分因子。
将双树复小波分解和四分偏微分方程两者相结合完成遥感数据去噪,详细的操作流程如图2所示。

图2 遥感数据去噪流程图
1)初始化遥感数据,确定迭代离散化时间和空间步长,设定迭代次数。
2)对含有噪声的遥感数据实施分解。
3)保留小波系数的低频部分,获取二阶差分。
4)通过遥感数据的实际情况和噪声水平选取合适的梯度阈值。
5)计算扩散函数的二阶差分。
6)获取去噪后的高频小波系数。
7)重构去噪后的高低频分量,获取去噪后的遥感数据。
2.2 异构遥感数据属性特征挖掘
在遥感数据去噪的基础上,挖掘其属性特征。选取遥感数据中的多个属性特征,主要包含波段、纹理以及形状等条件属性特征。以下分别对基元特征参数展开详细描述:
1)相似度:
主要用来衡量灰度共生矩阵元素在行或者列方向的相似矩阵,可以有效反映局部灰度值的相关性。相似度Cor的具体计算式如下所示

(4)
式中,q(i,j)代表矩阵元素值;uxuy代表局部灰度相关性;β1和β2代表度量矩阵的取值。
2)矩形度:
矩形度Compact主要用来描述目标图像面积和包围该图像的最小矩形面积之比,详细的计算式如下
(5)
式中,Mmerge代表对象的像元数量;nmerge和hmerge代表不同类型的对象像元。
另外,在计算的过程中,还需要使用最小外接矩形(MER),详细的计算步骤为:
1)追踪不同基元的四邻域轮廓,获取封闭区域;同时计算各个外接矩形面积,存储各个存储的长宽以及面积等信息。
2)重复步骤1),同时实施多次旋转。
3)当完成旋转之后,计算封闭区域的矩形面积,得到封闭区域的最小外接矩形,同时获取对应的顶点坐标。
4)根据步骤3)获取MER的顶点坐标,同时得到矩形的相关形状特征。
形状指数主要用来描述对象边的平滑度ShapeIndex,如式(6)所示
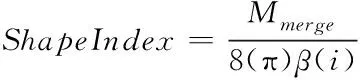
(6)
通过3D关联规则深度学习主要包含两个方面的内容,寻找全部的频繁项集以及通过频繁项集获取强关联规则。其中,强关联规则需要满足最小支持度和最小置信度规则。
基于3D关联规则深度学习的操作步骤如下所示:
1)预处理和挖掘任务存在关联的遥感数据,对问题具体分析并实施相应操作,构建结构化的数
2)对于数据库,需要求解全部满足最小支持度的项目集,即频繁项目集。
3)形成满足最小置信度的关联规则,进而构建规则集。
4)分析并解释典型的关联规则。
由于遥感数据量比较大且属性维数比较多,选择合适的3D关联规则深度学习算法是十分重要的。
通过3D关联规则深度学习算法分别统计式(4)-式(6)所描述的每个属性特征的期望信息和熵,进而获取异构遥感数据属性特征,如式(7)所示

(7)
式中,H(i,j)代表经过挖掘获取的异构遥感数据属性特征;Ent(H1)和Ent(H2)代表特征挖掘效率。
2.3 异构遥感数据检测
以通过3D关联规则深度学习得到的异构遥感数据属性特征挖掘结果为基础,采用计算机视觉常用的词包模型进一步实施异构遥感数据检测。过程如下所示:
1)将最优尺度作为判定依据,分割遥感数据,最终获取对应的数据对象;
2)获取每一个分割对象的低层特征[10],得到研究对象的底层特征描述符;
3)分别对分割对象的特征描述子进行编码量化[11]和聚类操作,将处理结果汇聚成特征字典;
4)通过判定依据,获取与研究对象距离较近的单个异构遥感数据,分别统计每个异构遥感数据出现的次数,进而得到各个研究对象对应的异构遥感数据,统一用词包表述。
设定遥感数据集可以分割为L个数据集lm,采用聚类获取r个聚类中心,获取字典B,将不同的B作为视觉单词,则有
B={b1,b2,…,bn}
(8)
计算全部异构遥感数据属性特征和视觉单词之间的欧式距离,同时将全部距离排序,选取距离最近的单词,将欧式距离表示为of,则对应的权重计算式为

(9)
式中,ϑi,j代表权重值。
由于词包模型忽略了遥感数据之间的空间关系,因此,还需要引入空间关系,对词包模型进行改进。在原始坐标信息内加入扩展特征,同时组建特征和空间位置共同影响的概率语义模型。为此,提出一种基于金字塔的多尺度词包模型,借助加权连接方法级联处理不同尺度下的单词,详细的操作步骤为:
1)分割原始遥感数据,获取多个分割数据集,构建标记矩阵遥感数据集合[12]。分别对原始遥感数据和标记矩阵遥感数据集合展开上下采样处理,以此为依据组建尺度金字塔。
2)组建视觉词汇字段,同时计算对应尺度下的异构遥感直方图。
3)将全部异构遥感直方图连接,构建联合直方图,最终得到对应的权重值。
以下采用基于多尺度词包模型检测异构遥感数据,详细的操作步骤为:
1)通过几何校正和辐射校正处理遥感数据[13]。
2)采用改进后的词包模型确定遥感数据的最优分割尺度,同时分割处理遥感数据,获取分割对象。
3)组建尺度金字塔影像,设定分割对象数量和金字塔层数[14,15],采用邻域窗口提取分割对象全部像素点的低层次特征,同时设定视觉单词数量,构建视觉词典。
4)根据视觉词典,分别对不同对象展开投影映射,形成视觉直方图,同时将其加权连接,获取多尺度直方图。
5)将全部特征映射到高维单词空间,最终实现异构遥感数据检测。
3 仿真研究
为了验证所提基于3D关联规则深度学习的异构遥感数据检测方法的有效性,进行实验验证。
实验主要选取精确率Precinion、召回率TPR、误报率FPR以及漏报率MAR作为测试指标,详细的计算式如下

(10)
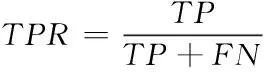
(11)
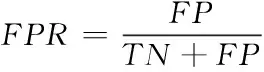
(12)
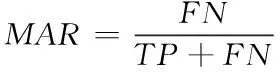
(13)
式中,TP代表检测异常且实际异常的样本数量;TN代表检测正常且实际正常的样本数量;FP代表检测异常且实际正常的样本数量;FN代表检测正常且实际异常的样本数量。
各个方法的检测性能表示为图3的形式。

图3 不同方法的检测性能测试结果对比分析
分析图3中的实验数据可知,由于所提方法对遥感数据实施了滤波处理,将数据中的噪声滤除,可以有效提升检测结果的准确性。
以下实验还进一步分析了各个方法在不同抽样次数下的异构遥感数据检测时间变化情况,实验结果如表1所示。

表1 不同抽样次数下各个方法的异构遥感数据检测时间结果对比
分析表1中的实验数据可知,所提方法可以以更快的速度完成异构遥感数据检测,其检测时间最低值与最高值分别为0.52s和1.24s,说明其具有较高的检测效率。
4 结束语
针对传统方法存在的一些问题,设计并提出一种基于3D关联规则深度学习的异构遥感数据检测方法。经实验测试证明,所提方法可以有效提升检测结果的准确性,同时还可以有效降低异构遥感数据检测时间,获取更加满意的检测结果。由于时间等多方面因素的限制,所提方法仍然需要展开更深层次的研究,确保其各项性能均得到有效提升,例如检测费用等。

