多源异构数据边缘融合信息化监测仿真

盛丽华,沈 晖

(南通大学信息化中心,江苏 南通 226019)

1 引言

多源异构信息作为社会经济活动中大量出现的非结构化、非标准化数据资源,对监测结果采集和分析有着至关重要的作用。由于计算机技术和互联网的不断进步,各项系统的结构日益复杂。系统内部数据类型开始复杂化和多样化,如何准确监测多源异构数据是现阶段研究的热点话题[1-2]。

国内相关专家针对上述内容展开了大量研究,例如涂梦昭等人[3]分析地下水存水量的变化趋势,构建利用GRACE卫星数据校准水文模型,通过模型完成地下储水量监测。王周虹等人[4]将网分装置采集的信息上调至调控主站,通过变电站内各种类型的配置描述文件,构建调控交互数据监测模型,利用信息之间的关联度将离散报文匹配分析处理,最终实现交互数据的监测。王军飞等人[5]主要通过PS点选取方法提取边坡数据特征,通过相干系数初选PS点,同时剔除极限误差点,最终获取PS点,实现数据监测。

在上述几种监测方法的基础上,提出一种基于边缘计算的多源异构数据融合信息化监测方法。实验结果表明,所提方法的实时性和监测性能均得到明显改善。

2 方法

2.1 多源异构数据预处理

半参数回归模型主要是由参数分量和非参数分量共同组成,具有比较强的解释能力。多源异构数据由于存在非线性误差,所以可以将观测模型表示为式(1)的形式:

s=Ha+s(t)+u

(1)

式中,s(t)代表和时间存在关联的函数,即非线性函数;Ha代表半参数回归模型;u代表多源异构数据中的噪声;s代表观测模型。

通过获取的多源异构数据,估计得到非线性函数对应的值,利用观测值减去全部线性值,进而构建观测模型为:

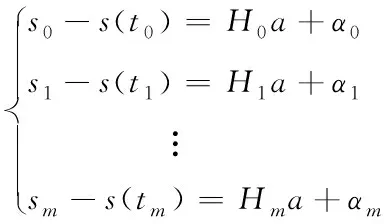
(2)

为了获取更加满意的去噪效果,引入小波阈值收缩法去噪处理。由于小波变换中的正变换具有比较强的相关性,可以有效分解信号的能量,获取信号在小波域集合中的小波系数。将半参数回归模型引入到小波阈值收缩方法中,将其应用于多源异构数据预处理中[6-7],详细的操作步骤如下所示:

1)对于全部的多源异构数,通过最小二乘多项式拟合处理,获取对应的拟合值集合D,如式(3)所示:

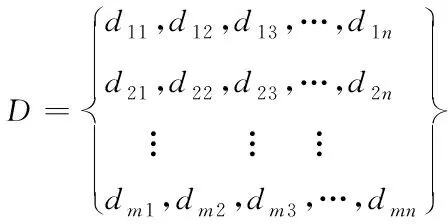
(3)

2)计算全部多源异构数据对应的残差值,如式(4)所示:

τ(x,y)=D·sgn(ω)-β(x,y)*s(t)

(4)

式中,τ(x,y)代表多源异构数据的残差值;ω代表噪声标准方差;β(x,y)代表半软阈值。

3)检验步骤2)获取的残差值是否为白噪声序列,假设是,则直接跳转至步骤5);反之,则继续下一步。

4)选取Daubechies小波对多源异构数据残差序列分解处理,获取小波系数。为了有效避免传统阈值方法存在的不足,引入半软阈值方法对多源异构数据预处理,采用Daubechies小波对去噪后的小波系数重构处理,进而估计出对应的非线性函数,同时跳转至步骤1)。

5)输出拟合值,完成多源异构数据预处理[8-9]。

2.2 多源异构数据融合

分析边缘计算的相关定义和技术特点,可以有效解决多源异构数据融合问题。优先给出多源异构数据标准化处理的详细操作步骤:

1)将采集到的多源异构数据通过时序特征分解处理,将B作为标准转换的输入,设定B以矩形的形式存在,如式(5)所示:

(5)

2)对多源异构数据的形成特点展开深入分析,融合全部类型的数据,进而完成数据变换处理,根据数据的类型制定对应的广义幂-标准分数标准化变换方案,即:

①假设B是以向量的形式存在,则可以直接得到变换处理后的向量结果;

②假设B的存储形式为矩阵,需要采用列向量计算全部数据的均值和标准差,对两者标准化处理,即可获取对应的结果矩阵;

③假设B的表现形式为多维数组,则需要根据维度信息对数据求解,得到与之对应的均值和标准差,对两者标准化处理,即可获取高维数据组。

3)将B采用广义幂-标准分数数据展开标准化处理B′,对应的矩阵为:

(6)

4)通过选定的多源异构数据处理方案对数据迭代处理,同时重复步骤2)和步骤3),完成迭代处理之后,将全部汇聚数据变换处理。

5)在完成多源异构数据的量纲和量级处理处理后,全部数据的格式均为统一的,可以将其直接传输到系统内存储,主要是为了简化后续多源异构数据的融合步骤,当全部数据完成标准化处理后,则停止计算。

在边缘计算模式下,多源异构数据的融合处理主要包含三个步骤,分别为:

1)信息融合处理;

2)状态评估方法;

3)关联决策。

(7)

式中,cm代表测试数据集;m代表测试数据集总数;t代表数据采集时间;E(u)代表随机两个成分之间的冲突程度。

多源异构数据融合的操作步骤如下所示:

1)对多源异构数据属性子集展开概率初始化处理,将R设定为多源异构数据融合模型的框架,则函数u:2u→[0,1]需要满足以下约束条件:

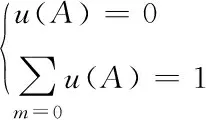
(8)

式中,u(A)代表多源异构数据之间的信任程度。

2)根据步骤1)设定的约束条件可以获取信任函数Bel(A),如式(9)所示:

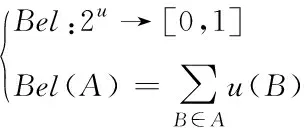
(9)

式中,u(B)代表全部子集分配概率值之和;A和B代表不同的多源异构数据融合集合。

3)设定多源异构数据融合似然函数,以此为依据确定全部数据特征属性的信任程度值。其中,数据属性成分对应的可信度ρ(a)可以采用式(10)计算:

(10)

4)计算多源异构数据融合的信任空间,进而获取信任函数和似然函数之间的关系表达式,如式(11)所示:

(11)

式中,τ(a)代表信任函数;pl(a)代表多源异构数据的特征度量结果;ς(a)代表似然函数。

5)通过构建的多源异构数据融合框架确定数据合成规则,根据不同源中数据特征属性索引完成特征级数据融合处理,最终完成数据融合处理[10-11]。

2.3 信息化监测

在完成多源异构数据的预处理和融合处理之后,采用隐半马尔可夫模型展开数据信息化监测。隐半马尔可夫模型是一种操作简单且效率高的随机模型,在各个研究领域内都得到了十分广泛的应用。

隐半马尔可夫模型ψ是由一个三元组成的,对应的表达式如式(12)所示:

ψ=(r,M,Z)

(12)

式中,r代表系统的初始状态概率;Z代表状态集合;M代表状态空间的转移概率矩阵,如式(13)所示:

(13)

在系统的调用序列中,可以将不同数据的排列组合看做是模型的不同状态。在数据使用过程中,需要更好完成数据的转换和衔接等操作,为后续的数据监测提供一定的数据支撑[12-13]。

将提取的特征向量设定为隐半马尔可夫模型的状态,则状态和转移可表示为图1的形式:

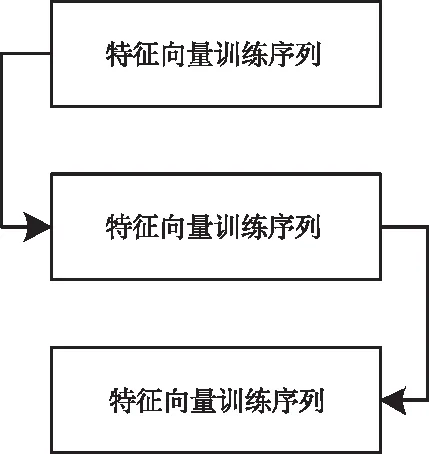
图1 隐半马尔可夫模型状态及转移图

隐半马尔可夫模型中的状态转移矩阵和初始分布可以通过对历史数据的观察得到。在训练数据中,为了完成数据的拓展,则隐半马尔可夫模型的状态转移概率为:

1)必要状态下的状态转移概率ϑij可以表示为式(14)的形式:

(14)

式中,Qij代表状态i向状态j转移的概率;Nij代表状态i向状态j转移的总次数;ε代表必要状态。

2)补充状态下的状态转移概率如式(15)所示:

ϑi(u,v)={Qij-ε}·Nij

(15)

随着多源异构数据的长度持续增加,经过计算可以得到各个观测序列的取值概率。但是在正常状态下,概率值会越来越小,无法将概率取值作为判断观测序列是否正常的依据。所以,需要对长度完全一致的观测序列展开监测更加有意义。

为了方便多源异构数据融合信息化监测,可使用以下的递推公式L(s):

(16)

式中,tu,v代表滑动窗口;对于滑动窗口而言,需要满足以下条件:

1)确定性:

对数据集训练处理,得到各个数据集对应的状态量,确保各个状态量在训练数量增加的情况下不会发生任何变化。

2)随机性:

将状态设定为变量,通过一种随机规则可以较好描述系统调用的随机性。

通过对隐半马尔可夫模型[14-15]的分析,建立和进程对应的随机模型,将研究系统内对应的调用序列设定为一个随机信号,全部信号均来自设定的信号源,同时进程具有特定的功能。由于大部分信号离散源是有记忆的,所以可以采用具有时间规律的条件熵展开衡量,同时设定隐半马尔可夫模型的状态序列长度H(x,y),对应的计算式为:

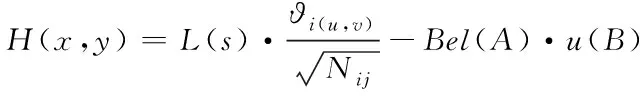
(17)

完成上述操作之后,将融合处理后的数据输入到隐半马尔可夫模型中,实现多源异构数据融合信息化监测。

3 实验分析

为了验证基于边缘计算的多源异构数据融合信息化监测(所提方法)的有效性,分别采取参考文献[3]方法与参考文献[4]方法做对比。实验选取Windows 2015作为实验平台,数据库为SQL,对应的组成架构如图2所示。

图2 实验架构示意图

采用不同方法对数据监测实时性展开测试处理,实验测试结果如图3所示。

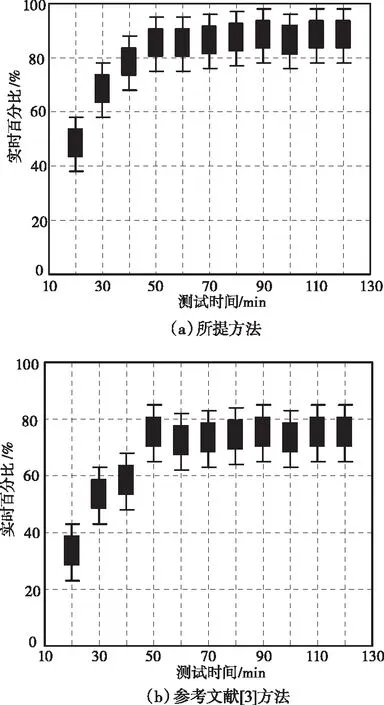
图3 不同方法的数据监测实时性测试结果对比

分析图3中的实验数据可知,各个方法的数据监测实时性会随着时间的变化而变化。在三种方法,所提方法的多源异构数据融合信息化监测实时性百分比均处于95%以上,而参考文献[3]方法与参考文献[4]方法的检测实时百分比在75%～80%之间,所提方法的实时性明显优于其它两种方法。

为了验证所提方法的监测性能,在设定时间内分析采用各个方法获取的多源异构数据融合信息化监测结果,实验结果如图4所示。

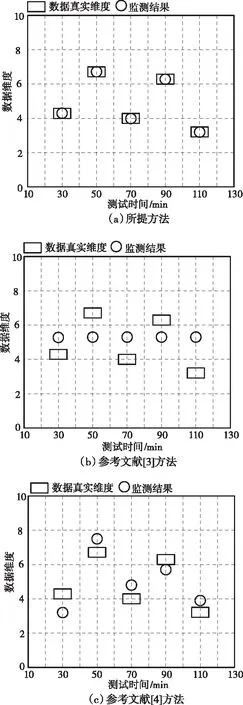
图4 不同方法的多源异构数据融合信息化监测结果对比

由图4中的实验数据可知,采用不同方法对多源异构数据融合信息化监测处理,经过对比分析证明,采用所提方法获取监测结果与实际值一致,而另外两种方法获取的监测结果和真实值存在较大误差。因此可以得出,所提方法的监测结果更加精准。

4 结束语

为了准确监测融合处理后的数据变化情况,提出一种基于边缘计算的多源异构数据融合信息化监测。采用小波阈值去噪方法对多源异构数据预处理,消除其线性误差。构建多源异构数据融合架构,完成数据融合处理,并将其输入到隐半马尔可夫模型中,实现多源异构数据融合信息化监测。经过实验测试证明,所提方法可以获取高精度的监测结果,且监测实时性明显优于其它方法。在后续研究过程中,对所提方法展开更加全面的优化处理,可以进一步增加多源异构数据来源的广度,例如监测对象的声音信号以及生产计划等,充分利用多源异构数据的优势。