基于窄带物联网的信息压缩存储方法.

桑 振,胡 建

(河北农业大学,河北 保定 071000)

1 引言

伴随互联网和物联网等技术的逐渐成熟,各类数据量呈爆发式增长,其中蕴含大量具有科学价值与应用价值的信息,其不仅能为互联网带来发展机遇,还能为人们生活生产提供更好的服务。但与此同时,网络也时刻都需要面临海量数据的采集、分析、存储问题,再通过挖掘不同用户数据中的有效信息,创造符合用户需求的服务,从而提升产业价值。然而信息大爆炸时代的到来使大数据集快速、有效存储成为互联网公司当前面临的新挑战[1,2]。已有存储设备易发生老化、故障等情况,且难以确保信息绝对安全传输,导致信息丢失或泄露现象频发。另外,已有存储设备的内存空间有限会约束存储信息的规模,导致其对大数据集的存储和传输能力较差,且有关技术的发展速度与数据集规模扩大速度不匹配[3],因此,信息压缩存储方法逐渐引起相关领域的关注。该方法是指通过使原信息损失或不损失的形式,对重复信息进行压缩,以达到信息数据量降低、存储空间减少的目的,包含可扩展性良好、负载均衡、成本较低等优势,是影响大数据集存储最深远的一项技术。

很多相关专家学者均在此类技术的研究上取得杰出成就,例如杨耀森[4]等人使用多核架构实现对图像信息的压缩存储,该方法的信息传输速率高达35MB/s,且兼容性较高,但方法架构不能完全适应所有应用系统。王鹤[5]等人使用分布式压缩感知和边缘计算实现对电力信息的压缩存储,该方法压缩后的信息完整性较高,且通信开销大大降低,但对大规模数据的计算复杂度有待提升。

窄带物联网是万物互联网络的重要组成部分,具有带宽消耗低等特点,能实现较高要求设备的高效连接,且能提供全面的数据连接覆盖。因此,本文提出基于窄带物联网的信息压缩存储方法,通过移动采集感知层、网络层和应用层的相互协作,实现信息压缩存储,以满足目前不断增长的大数据集有效存储需求。

2 信息压缩存储方法研究

2.1 基于窄带物联网的信息管理模型

引入窄带物联网对信息进行管理,构建如图1所示的基于窄带物联网的信息管理模型。

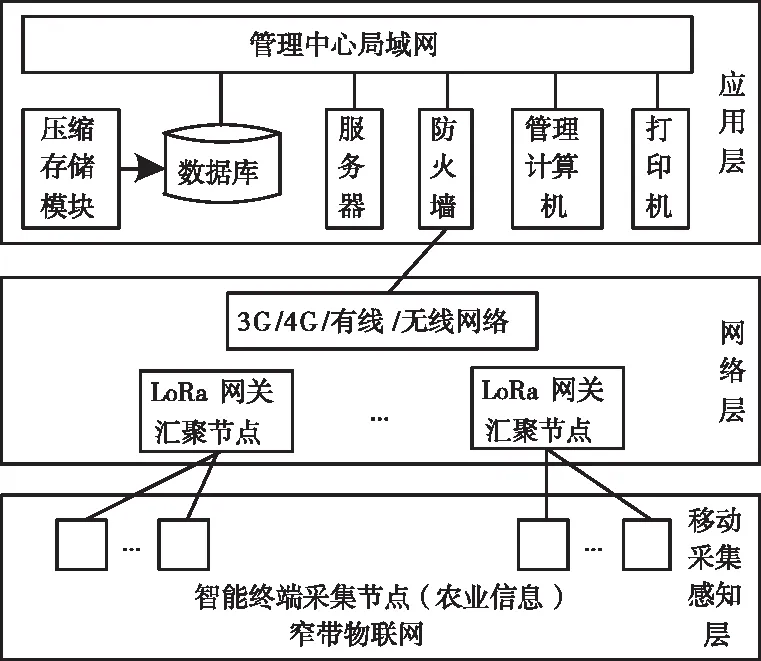
图1 基于窄带物联网的信息管理模型

图1中,LoRa网络和若干智能终端采集装置共同构成移动采集感知层,该网络以星型网络作为架构,该装置能够自主获取需要的农业信息,使用LoRa网络将所得信息传输到网络层的LoRa网关汇聚节点;TCP/IP协议包含于汇聚节点内,其接收到传输的信息后,经过整合处理将信息传输至应用层;应用层是信息管理模型的核心部分,包含压缩存储模块、数据库、管理计算机等。其中,压缩存储模块通过基于规范Hadamard矩阵的信息压缩存储方法对接收到的信息进行压缩存储,并将结果保存至数据库,用户利用管理计算机可以操作数据库中的信息,以及查看返回结果。

2.2 Hadamard矩阵及其特点

该矩阵在信息处理、通信等领域应用十分广泛。假设A=(aij)表示实数方阵,其阶数用m描述,该方阵满足式(1)所示表达式

(1)

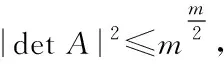
设置Hadamard矩阵阶数为m,如果它是行规范的H-矩阵,那么该矩阵满足第一行元素均为1;如果它是列规范的H-矩阵,那么该矩阵满足第一列元素均为1;如果它是规范的H-矩阵,那么该矩阵应该同时满足上述两个条件[6,7]。下述为Hadamard矩阵性质。

H-矩阵用Hm描述,其阶数为m,可获得如式(2)所示表达式

(2)

若H为H-矩阵,通过行或列换序、多行或多列与-1相乘、转置操作的任意组合处理H,获得H′,其仍是H-矩阵。

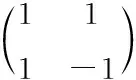
(3)

式内,h1j和h2j相加等于±2或0,h1j和h3j相加同样等于±2或0,所以可得,上式各项与等号左边均为4的倍数[8]。

假设H是m阶H-矩阵,能得到2m阶H-矩阵。若某整数用t描述,其值大于等于0,则存在2t阶H-矩阵。

在上述Hadamard矩阵性质的基础上,可将其描述为式(4)所示的递推关系

(4)

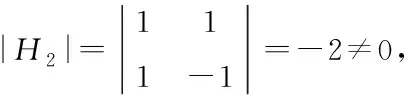
(5)

通过上述内容得出,Hadamard矩阵为满秩矩阵,且经过初等变换所得结果仍为满秩矩阵。

2.3 矩阵在计算机中的存储

假设存在n阶矩阵,采用n维数组描述其在计算机内的形式,抽象数据对象数组表达式用式(6)描述

Array{D={aj1,j2…jn}|j=0,…,bi-1,i=1,2,…,n}

(6)

式内,数组维数用n描述,其值大于0;处于i维位置,数组的维界用bi描述;处于i维位置,数组元素的下标用ji描述;数组元素用aj1,j2…jn描述。

在n等于1的条件下,可使用长度固定的线性表描述n维数组;在n大于1的条件下,可将n维数组看作线性表位于n维空间的拓展,因此可将二维数组的各元素看作长度固定的线性表。以式(7)描述的数组为例,具体如下

A={am-1,n-1}m×n

(7)

能够将上式当作线性表,用A=(α0,α1,…,αp)描述,且p=m-1或p=n-1。

若各元素为行向量线性表,则p=m-1,用αi=(αi0,αi1,…,αi,n-1)描述,且0≤i≤m-1;若各元素为列向量线性表,则p=n-1,用αj=(α0j,α1j,…,αm-1,j)T描述,且0≤j≤n-1,使矩阵A变成一维数组的存储形式。

若二维数组将行序当作主序,其占用的存储单元数量为L,可利用下式描述某元素αij的存储地址

Loc(i,j)=Loc(0,0)+(b2·i+j)L

(8)

式内,元素的基址用Loc(0,0)描述。上式可转换为式(9)所示形式,是在维界等于b1、b2的情况下

Loc(b1-1,b2-1)=Loc(0,0)b1b2L

=Loc(0,0)+[b2·(b1-1)+b2]L

(9)

将上式的L和Loc(i,j)=0分别设置成1、0,可使用b1b2描述二维数组的归一化存储空间[11,12]。

2.4 基于规范Hadamard矩阵的信息压缩存储方法

根据Hadamard矩阵定义,N阶规范Hadamard矩阵具有对称性,其中N=2m、m∈Z。通常使用上、下三角N阶矩阵完成对称矩阵的存储。

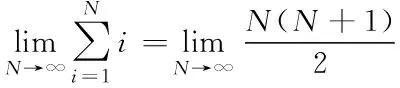
设置一维数组用h[N(N+1)/2]描述,将其当作阶数为N的规范Hadamard矩阵的存储结构,那么h[k]与各元素aij相互匹配,具体用式(10)描述

(10)

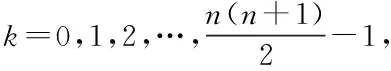
3 实验与结果分析

以某市东北方向农业区域作为实验对象,使用本文方法采集106条农业信息,根据领域将所得信息划分成10个子集,通过本文方法实现采集信息的压缩存储,以验证该方法的有效性。

引入压缩比衡量信息压缩效果,其值越大,压缩性能越优异,计算过程为:(1-压缩后大小/压缩前大小)×100%。不同信息规模下,使用本文方法与未使用本文方法的压缩时间、解压缩时间、压缩比结果用表1描述。

表1 不同信息规模的信息压缩结果

分析表1可以看出,随着信息规模不断扩大,本文方法使用前后的压缩时间和解压缩时间均呈上升趋势。相较于本文方法使用前,使用本文方法后的两个时间都节约50%以上,本文方法后的压缩比始终在75%～90%之间变使用化,而本文方法使用前的最大压缩比仅为45.3%。对比以上结果表明,本文方法的信息压缩效果良好且效率高。

使用本文方法对土地信息集进行压缩存储,其中信息高度密集区域及其经过压缩处理后的可视化结果用图2描述,图中方块表示信息。通过分析图2中的结果可以看出,信息高度密集区域的信息规模较为庞大,存储时会占用较多存储空间,使用本文方法处理后,该区域的信息量大大降低,且能将描述该区域基本特征的临界信息保留,因此表明,本文方法具有较优异的信息压缩效果,对降低存储空间压力起着重要作用。

图2 土地信息集的压缩效果

使用本文方法对10个农业信息子集进行压缩存储,各子集的信息失真率结果用图3描述。

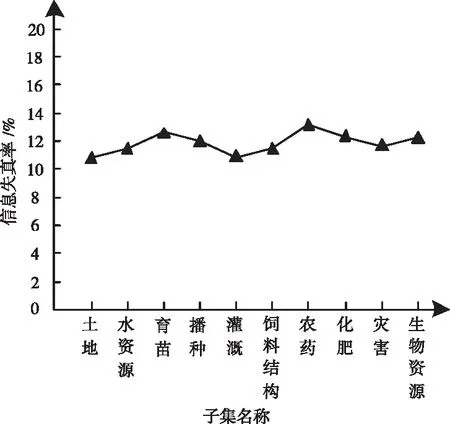
图3 不同子集的信息失真率结果

通过分析图3中的结果可以看出,经过本文方法处理后的各子集信息失真率均处于10%～14%之间,其中信息失真率最高和最低的子集分别为农药、土地,值为13.5%、10.5%左右。由此可知,本文方法的信息压缩存储效果较理想,存储的信息失真率较低,真实度高。

测试不同信息子集分别采用直接存储,以及本文方法的压缩存储所需信息存储空间,结果用图4描述。通过分析图4中的结果可以看出,对各信息子集采用直接存储方式时,所需信息存储空间在700～900Mb范围内变化,使用本文方法进行各信息子集压缩存储时,所需信息存储空间始终低于200Mb,存储空间节约71%～78%左右。以上结果表明,本文方法的信息压缩存储效果优势显著,可极大地减少存储空间。

图4 不同信息子集的信息存储空间结果

4 结论

随着互联网普及范围逐渐扩大,以及各行各业的快速发展,每日都会产生海量信息,给现有存储设备带来巨大压力,针对这一背景,本研究提出基于窄带物联网的信息压缩存储方法,解决了当前存在的信息冗余过大和存储设备的存储空间与信息增长量不匹配等问题。该方法通过创建基于窄带物联网的信息管理模型,结合基于规范Hadamard矩阵的信息压缩存储方法,实现大规模信息压缩存储。经实验验证可知,该方法具有良好的信息压缩效果,且压缩效率较高。该方法通过信息压缩存储能使信息存储空间大幅度减少,因此,其能够为数据挖掘领域和互联网的进一步发展提供支持。