基于顶点轮廓的鲁棒性抗前景干扰稳像算法

尹丽华,康 亮,刘士建

(1. 上海第二工业大学,上海 201209;2. 中国科学院上海技术物理研究所中国科学院红外探测与成像技术重点实验室,上海 200083)

1 引言

利用手机、数码相机等设备拍照时,视频抖动的存在不仅会影响视觉效果,而且容易影响各种后续的计算机视觉任务,例如,目标识别或跟踪精度。因此,视频稳像技术至关重要。目前该技术面临如下的难点:如何处理有视差变化或运动前景干扰下的视频,同时保证稳像精度。

根据所采用运动模型[1]不同,目前电子稳像方法主要归为三类:2D、3D和2.5D方法。其中,2D模型最为简单,通常是利用单个仿射模型来表示帧间的运动,并通过各种滤波方法平滑相机路径。为了解决视差变化的稳像难题,Liu提出了基于捆绑相机路径的模型[2],通过捆绑模型来替代单个模型。后来,于文杰又提出基于多路径优化的稳像方法[3],通过对图像进行网格划分结并采用多路径优化策略实现稳像,但是当特征点受遮挡时,该算法的稳像效果会受到限制。3D方法是利用复杂的三维重建实现稳像,该方法虽能处理视差问题,但是复杂度较高,实时性较差。通常2D和3D方法需要依赖于长特征轨迹的跟踪,后来结合2D和3D方法的优势,很多学者又提出2.5D方法[4-6],该方法避免了脆弱的特征跟踪,Liu 在二维特征轨迹上应用低秩子空间约束[4],后来又利用极间转移技术增加特征轨迹的长度,但该方法在复杂场景视频中并不成立,比如拥堵的交通道路场景和密集的人流[5]。

为了解决运动前景干扰的难题,Shene曾提出将SURF算法和随机抽样一致性(RANSAC)算法相结合剔除异常点[7],但该算法只能剔除部分的前景特征点。后来,朱娟娟又提出基于三帧差分的稳像算法[8],该算法对简单场景的效果较好,但不适用于大范围前景的情况;谢亚晋等提出基于最小生成树与改进卡尔曼滤波器的视频稳像方法[9],提高了稳像精度,该算法当处理复杂前景干扰时的效果有限;Wu结合RANSAC和K-means聚类方法进行前景剔除[10],但该方法只适用于含大范围运动前景的情况。后来,北京理工大学的杨佳丽结合陀螺仪数据进行运动估计,利用李群流形上的卡尔曼滤波进行平滑[11],但是稳像精度很容易受陀螺仪设备精度的限制。后来,Liu等提出SteadyFlow算法[12],属于2.5D方法,用像素轮廓代替特征轨迹,但计算效率较低。在文献[13]中,Zhao又提出综合利用前景和背景的特征轨迹实现视频的稳定,该算法虽提高了交通场景下的稳像精度,但对复杂场景的适用性则较差。另外,近年来深度学习技术在计算机视觉任务中也取得了巨大进步[14-16],比如在稳像方面,Wang等人提出第一个StabNet深度学习稳像网络[14],该网络根据输入的抖动视频序列学习一组抖动视频到稳定视频的映射。XU等人提出使用生成对抗网络进行视频稳像[15],属于监督式的学习,上述两种方法都需要用到大量的稳像视频对数据集,获取难度较大,而且实时性较差,不能满足工程应用的需求。

综上可知,目前的稳像方法主要适用于简单场景,在当处理有大范围和多运动前景干扰的情况时,仍有一定的局限性[17]。因此,结合2.5D方法的优势,本文提出一种基于顶点轮廓的鲁棒性抗前景干扰稳像方法,该算法的创新性主要体现在:首先,用顶点轮廓代替像素轮廓和特征轨迹,根据运动矢量的相似性生成了基于网格顶点的稀疏运动矢量,剔除了运动前景的干扰,同时提高了算法的效率;其次,利用时间分析法识别出具有不连续运动矢量的网格顶点,并通过中值滤波器f2对网格顶点处的运动矢量补全,进一步剔除了复杂运动前景的干扰。

2 算法原理

本算法的流程如图1所示。

算法流程描述如下:

1)对输入视频检测FAST特征[18]。

2)生成稀疏运动矢量。将图像划分为m×n网格,利用基于金字塔的Lucas-Kanade光流算法得到特征匹配对;并根据运动矢量的相似性,利用中值滤波器f1生成基于网格顶点的稀疏运动矢量。

3)稀疏运动矢量的空间平滑。为了能有效剔除复杂运动前景的干扰,本文先通过时间分析法识别出具有不连续运动矢量的网格顶点,并剔除“离群”顶点对应的运动矢量;并利用中值滤波器f2对网格顶点处的运动矢量补全,实现运动矢量的空间平滑。

4)对不同时刻基于网格的运动矢量进行累加,形成顶点轮廓。

5)通过路径平滑策略,对顶点轮廓进行平滑。

6)对图像进行反向补偿,输出稳定视频。

2.1 生成基于网格顶点的稀疏运动矢量

将图像划分为m×n的网格,利用基于金字塔的Lucas-Kanade(简称LK)算法[19]得到特征匹配对,计算部分特征点的运动矢量;然后,利用中值滤波器f1将已知运动矢量扩展到它附近的网格顶点,得到网格顶点的运动矢量,并用它生成顶点轮廓。

本算法利用采用顶点轮廓,而非像素轮廓和特征轨迹。下图2给出了特征轨迹、像素轮廓、顶点轮廓的对比,其中,图2(a)代表特征轨迹,该特征轨迹由第t-1帧中特征点像素A->第t帧中的对应像素B->第(t+1)帧中的对应像素C构成,由于运动前景的存在,获取长特征轨迹的难度较大。图(b)代表像素轮廓,是同像素点在一段时间内的运动矢量构成,该方法需要收集所有像素点的运动矢量,因此计算效率比较低;图(c)代表顶点轮廓,仅收集每个网格顶点处的运动矢量,不仅能避免脆弱的特征的跟踪,而且相对于像素轮廓,因此,顶点轮廓的运算效率能得到提高。

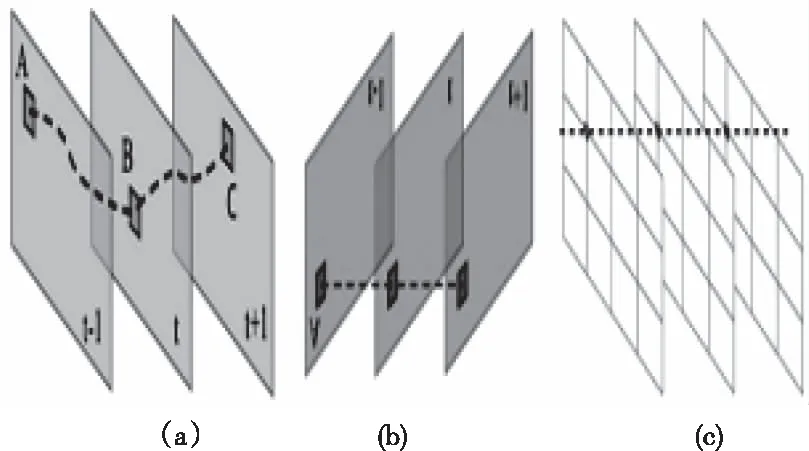
图2 特征轨迹、像素轮廓、顶点轮廓的对比

2.1.1 FAST特征匹配

利用基于金字塔的Lucas-Kanade光流算法通过由粗到精的搜索策略实现特征匹配。在图像J中找到图像I中特征点μ所对应的特征点ν,匹配过程的描述如下:

a) 对图像I和图像J建立高斯金字塔。

c) 根据上层计算结果,并利用迭代计算(L-1)层的残差光流向量d(L-1);

d) 接着,估计(L-1)层的光流量:

gL-1=2(gL-1+dL)

(1)

e) 重复步骤(c) (d),直至L=0,估计出最终光流f=g0+d0,最终,在图像J中找到图像I中特征点μ所对应的特征点ν,即ν=μ+f。

2.1.2 运动矢量的扩展

运动矢量扩展的过程如图3所示。

图3 运动矢量扩展的示意图

Step1:首先,利用FAST特征点对的匹配结果,计算各个特征点所对应的运动矢量。

如图(a)所示,图中{p,p′}代表第t帧和第t-1帧中的FAST特征点匹配对,红点代表特征点位置,虚线箭头代表运动矢量,则特征点p处所对应的运动矢量vp为

vp=p′-Ftp

(2)

式中:Ft表示全局单应性矩阵。

Step2:以特征点p为中心,建立一个r1×r1圆形模板,如图(b)所示。

Step3:根据运动矢量的相似性,采用中值过滤器f1,将该过滤器的响应分配给圆形模板中其它的网格顶点,如图(c)所示。由于所有匹配的特征都会将运动矢量传播到其附近的网格顶点,因此,同一个网格顶点可能接收多个运动矢量。本文中采用中值过滤器f1,将过滤器的响应被分配给网格顶点。对第t帧图像,网格顶点q的运动矢量ut(q)为

ut(q)=med{vp,p∈Ωq}

(3)

式中,Ωq表示网格顶点附近位于它r1×r1圆形模板内的所有特征点。

图4为利用中值滤波器f1对网格顶点运动矢量估算的示例。图中,红色“○”表示特征点,网格顶点(蓝色☆)受到多个运动矢量的影响。

图4 利用中值滤波器f 1对网格顶点运动矢量估算的示例

2.2 稀疏运动矢量的空间平滑

受复杂运动前景干扰的影响,图像的稀疏运动矢量往往不连续,直接补偿会导致稳像后图像出现“渲染”伪像。因此,需要剔除复杂运动前景的干扰。本文中提出对运动矢量进行空间平滑,先通过时间分析法,识别出具有不连续运动矢量的网格顶点,剔除“离群”顶点对应的运动矢量;并利用中值滤波器f2对顶点处的运动矢量补全,实现平滑。

2.2.1 时间分析法

对于第t帧图像,网格顶点q处的运动矢量Wt(q)是对多组运动矢量ut(q)进行累加得到的结果,具体的定义如下

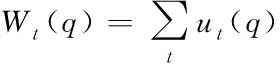
(4)

式中:ut(q)为顶点q在第t帧的运动矢量。

时间分析法基于如下假设:对包含背景和运动前景的运动轨迹,背景区域内顶点的累积运动矢量Wt(q)在时间上通常应该是平滑的,而运动前景区域内的网格顶点的累积运动矢量Wt(q)在时间上往往具有不连续性。

因此,本算法中通过判断累积运动矢量的轨迹是否在时间上光滑识别不连续运动矢量,同时,使用掩模Mt(q)来记录第t帧图像中的顶点q是否离群,Mt(q)定义如下

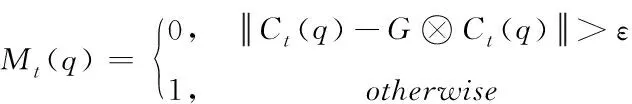
(5)

式中,G为高斯滤波器(默认的标准偏差为3),如果离群,则令Mt(q)=0,否则令Mt(q)=1。

2.2.2 运动矢量的补全策略

形成离群点掩模后,需要更新并补全对应顶点处的运动矢量,并分以下两种情况:

第一种:如果Mt(q)=1,则该网格顶点处的运动矢量仍然保持不变。

第二种:如果Mt(q)=0,剔除将该网格顶点处的运动矢量,并利用中值滤波器f2对该点处的运动矢量进行补全。以顶点q为中心,通过r2×r2的方形模板进行覆盖,则最终运动矢量为中值滤波器的响应,公式如下

ut(q)=med{ut(k),k∈Wq},WhenMt(q)=1

(6)

式中,Wq表示以网格顶点q为中心,位于附近它附近r2×r2方形模板内的所有顶点。

运动矢量空间平滑的示例如图5所示,其中,图(a)表示原始运动矢量,图(b)为识别出运动前景上的网格顶点,图(c)为运动矢量平滑后的局部效果图,从图中可以看出,本算法能有效识别出运动前景,剔除前景的干扰。

图5 运动矢量空间平滑的示例

2.3 生成顶点轮廓

在顶点轮廓生成之前,为了保证算法的鲁棒性,本文算法中先使用全局单应性Ft为所有顶点得到全局运动矢量场Vt,则第t帧图像中第i个网格顶点对应的最终运动矢量y为ut′(i)=Vt(i)+ut(i)。

第t帧图像中第i个网格顶点的顶点轮廓Ct(i)是通过对所有时间点的运动矢量累加得到,即

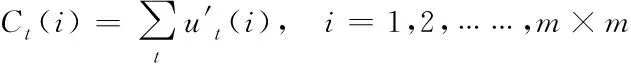
(7)

式中:ut(i)为第t帧图像中第i个网格顶点所对应的运动矢量,相同方法可得到其它顶点轮廓。

图6为不同位置网格顶点处的运动轨迹对比,从前、后三帧图像中抽出两个特殊网格顶点处位置,顶点1位于背景上,顶点2位于运动前景上。图(a)中顶点1用☆表示,网格顶点2用○表示,不同时刻用红色、绿色、蓝色来区别。

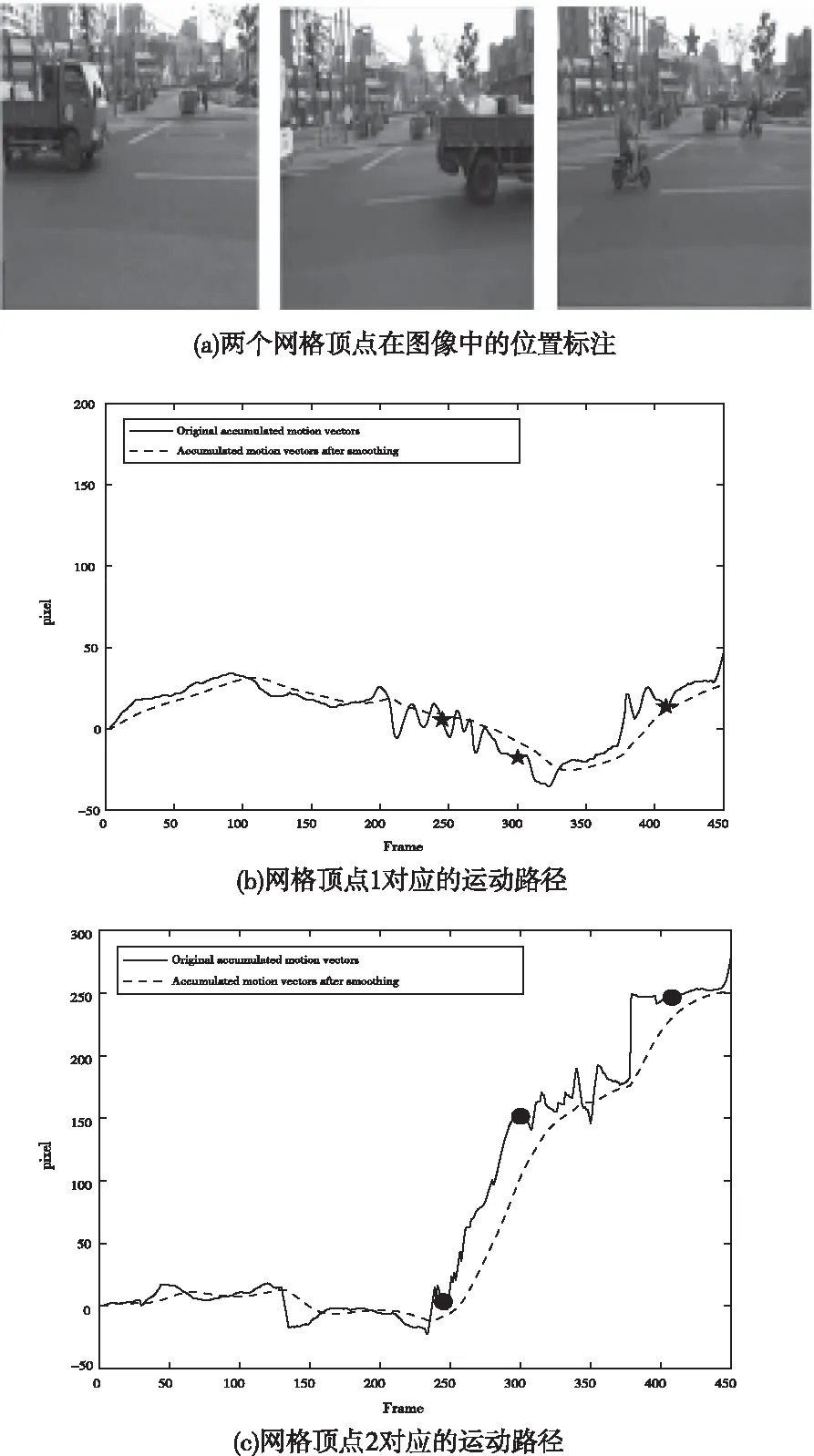
图6 不同网格顶点处的运动路径对比

图(b)为网格顶点1对应的运动路径,图(c)为网格顶点2对应的运动路径。由图(b)的运动曲线可以看出,顶点1始终位于静态背景上,所以它的累积运动向量在时间上是存在少量的高频分量,处理后的路径也更加平滑。由图(c)的运动曲线可以看出,顶点2位于运动前景上,由于有移动的车辆经过,未平滑前运动曲线时具有大量的高频分量,经平滑后的运动曲线,剔除了高频分量,真正起到了抗前景干扰的作用。

2.4 基于顶点轮廓的稳定

为了路径的优化,希望避免出现过度的裁剪以及稳定化后的扭曲问题,采用最小化目标函数来实现顶点轮廓的平滑

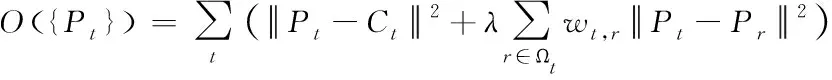
(8)

其中,顶点轮廓Ct为原始路径,希望的是得到最优路径Pt,P和C均是非参数的累积运动向量。

3 结果与讨论

为了能有效说明该算法的优势,本文实验主要从以下三个方面展开:首先,从数据集中选出受大范围和多个运动前景干扰下的视频进行稳像实验;其次,从数据集中选出六组含运动前景、视差变化、旋转或缩放的视频进行稳像实验,验证算法的鲁棒性;最后,将本文算法和传统算法的实时性进行了对比。

另外,本文的验证实验均是在硬件环境为 Intel(R) Core(TM)i5-5200U CPU@2.20GHZ,8GB内存,64位Win10的系统上进行的,采用Python3.8.6软件平台,并依赖Opencv图像处理库以及CVX安装包。

3.1 受大范围和多运动前景干扰下的稳像结果

从多个公共数据集[20,21]中选出复杂前景干扰下的两组测试视频,如下图7所示,图(a)为受大范围运动前景干扰的视频组,图(b)为受多个运动前景干扰的视频组。

图7 复杂前景干扰下的两组测试视频

为了说明本文算法对于复杂前景干扰下视频的稳像优势,分别采用传统稳像算法Liu[2]、Wu[10]、Zhao[13]和本文算法进行稳像,并计算出两组视频下采用各算法后的峰值信噪比(PSNR),两组视频下的PSNR结果分别如下表1、表2所示,表1为受大范围运动前景干扰下的PSNR值,表2为受多个运动前景干扰下的PSNR值。

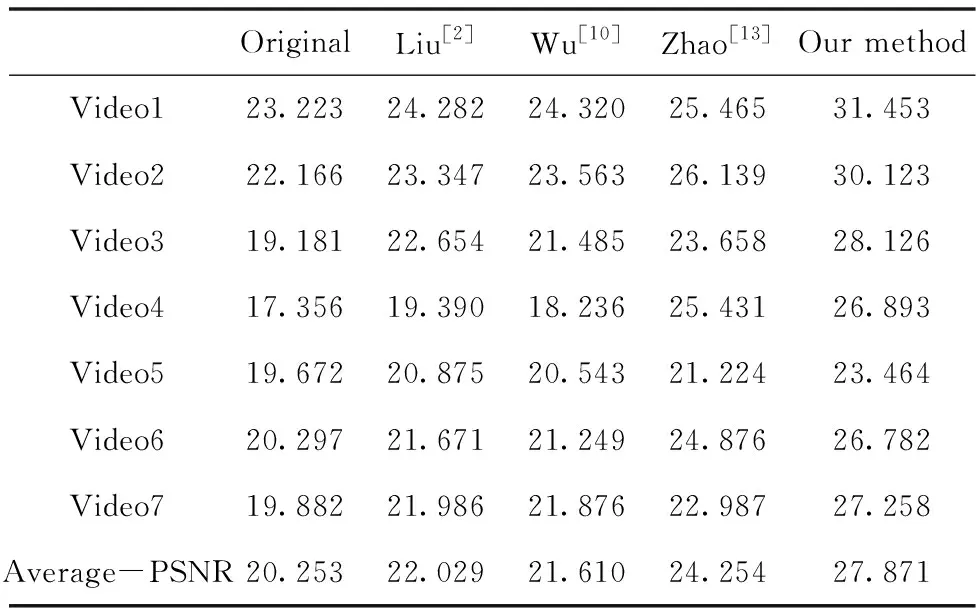
表1 大运动前景干扰下视频的PSNR值

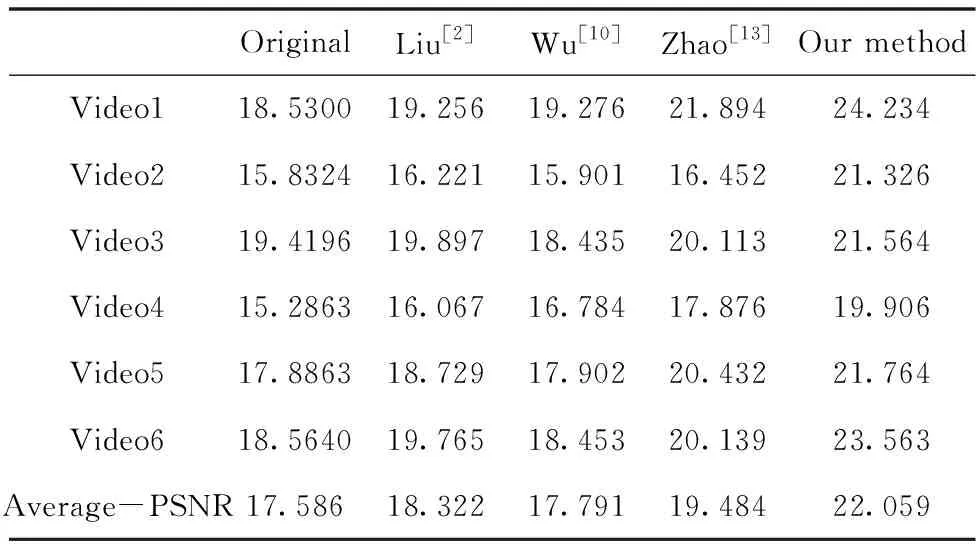
表2 多运动前景干扰下视频的PSNR值

峰值信噪比(PSNR)常用来衡量视频的稳像质量好坏,主要反映了参考图像和当前图像间的峰值信噪比,定义如下

(15)

式中,Imax是最大亮度值,MSE(I1,I0)表示连续帧间的均方差。PSNR值越大,则说明帧间的灰度差越小,图像稳定的效果越好。

由表1可以看出,在大运动前景干扰下,本文算法的平均PSNR值为27.871,比三种传统的算法Liu[2]、Wu[10]、Zhao[13]的PSNR值提高更明显,与近年的Zhao[13]算法相比,PSNR值提高了14.9%(即(27.871-24.254)/24.254*100%=14.9%)。由表2可以看出,在多运动前景干扰下,本文算法的平均PSNR值为22.059,比三种传统算法Liu[2]、Wu[10]、Zhao[13]的PSNR值提高更明显,与近年的Zhao[13]算法相比,PSNR值可以提高13.2%(即:(22.059-19.484)/19.484*100%=13.2%)。

因此,综合表1、表2中的数据可以看出结论,在复杂运动场景的干扰下,本算法比传统算法PSNR值提高更明显,更具有稳像优势。

另外,为了能直观比较各算法的稳像效果,下图(8)、和图(9)分别为受大范围、多个运动前景干扰下的稳像结果,其中,图(a)为原始图像帧,图(b)为Zhao[13]算法的稳像结果,图(c)为本文算法的稳像结果。

通过图8(b)、图8(c)的结果对比,可以看出经本算法稳像后的图像边缘区域更少,视频过渡更加平滑,视觉效果更好,这说明本文算法不仅能更好的剔除大范围运动前景的干扰。通过图9(b)、图9(c)的结果对比,可以看出,本算法对多个运动前景干扰的情况也能实现不错的视觉稳像结果。

图8 受大运动前景干扰下的视频稳像结果

图9 受多个运动前景干扰下的视频稳像结果

3.2 验证本文算法的鲁棒性

从公共数据集中选出六组含运动前景、视差变化、旋转或缩放的测试视频进行实验,验证鲁棒性的测试视频如图10所示。

图10 验证鲁棒性的测试视频

接下来,将本文算法与四种传统稳像算法Subspace[4]、Epipolar[5]、Bundled-paths[2]、SteadyFlow[12]进行客观评价指标的对比。评价指标分别采用:Cropping Ratio(裁剪率)、Distortion(失真率)、Stability(稳定度)。

图11为各算法的稳像指标对比,通过对比可以看出,当处理包含运动前景、视差变化、旋转或缩放的视频时,本文算法相对于传统算法,裁剪率、失真率和稳定度三个指标方面表现较好,充分说明该算法具有鲁棒性。

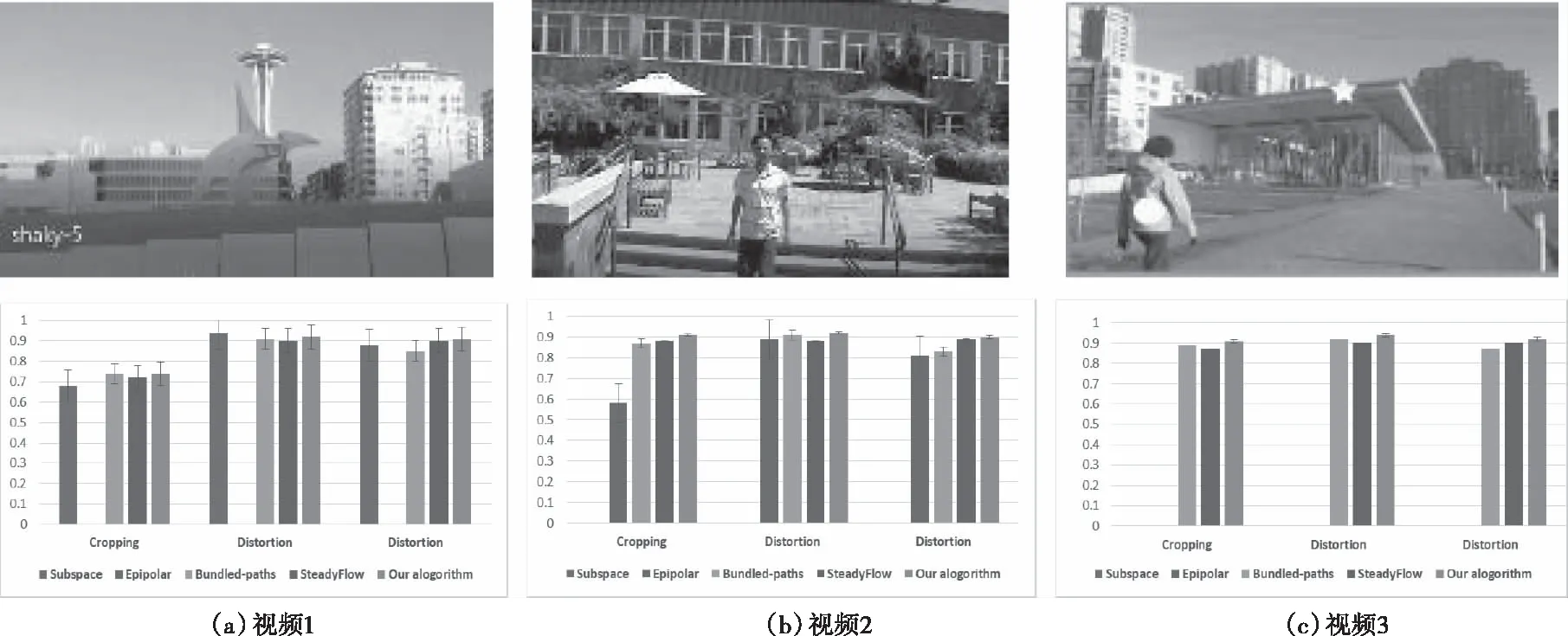
图11 各算法的稳像指标对比

3.3 运行时间比较

从数据集中选取出分辨率为720×1280,360×640,480×272的三组测试视频,视频中均包含了复杂运动前景,本文中分别采用了SteadyFlow[12]、Zhao[13]和本文算法进行稳像实验,各算法的运行时间结果如表3所示。

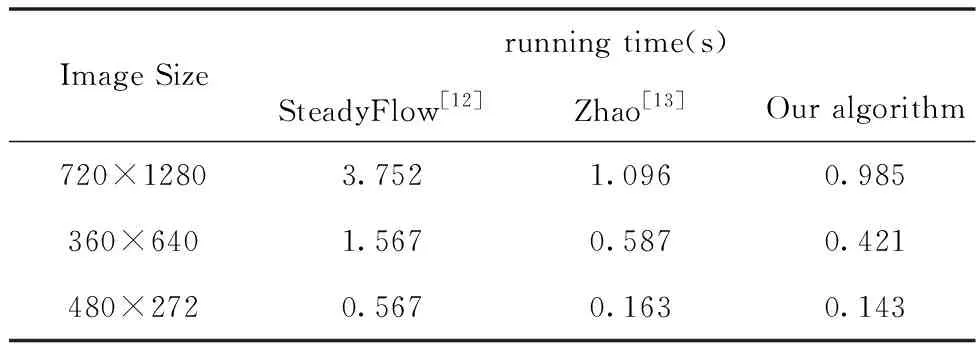
表3 各算法的运行时间结果

通过表3中各算法运行时间,可以看出,在三种不同图像尺寸下,SteadyFlow算法[12]的运行时间分别约为本文算法运行时间的3.8倍、3.7倍、3.9倍,本算法的实时性更具优势,主要是因为本算法仅需要收集每网格顶点处的运动矢量,运动矢量场稀疏化,因此运算效率得到明显提高。另外,虽然本文算法与Zhao[13]算法相比,运行效率也得到一定程度的提高,但本文算法的稳像精度比Zhao算法[13]更高,本文算法的稳像精度和实时性能满足工程应用的实际需求。

4 结论

为了解决复杂运动前景对稳像精度干扰的难题,本文提出一种基于顶点轮廓的鲁棒性抗前景干扰稳像方法,实验结果表明,该算法在裁剪率、失真率和稳定度三个指标方面表现较好,运算效率更高,更能满足稳像算法的实时性要求。但本算法对于背景比较复杂的情况仍有一定局限性,需要后续进行深入研究。