构建有效问题链 提升数学学习力*
——以“变量与函数”为例
童 佳
⦿ 湖北省武汉市粮道街中学
1 教学立意
课程标准认为,数学学科核心素养主要表现为会用数学的眼光观察世界,会用数学的思维思考世界,会用数学的语言表达世界.如何在教学中落实好呢?关键是要结合相应的教学内容,在落实“四基”“四能”的过程中,促进学生数学学科核心素养的形成与发展.而基于学情设置有效的问题链就是一种有效的方法,它激发学习动力,锻炼毅力,培养创造力,提升学习能力.
下面,以“变量与函数”为例来探讨如何构建有效的问题链,提升学生数学学习力.
2 教学过程
2.1 创设问题情境,激发学习动力
问题1生活中有许多运动变化的事物,请大家观察图1中的两幅动态图片,其中分别有哪些变化的量呢?它们是怎么变化的呢?
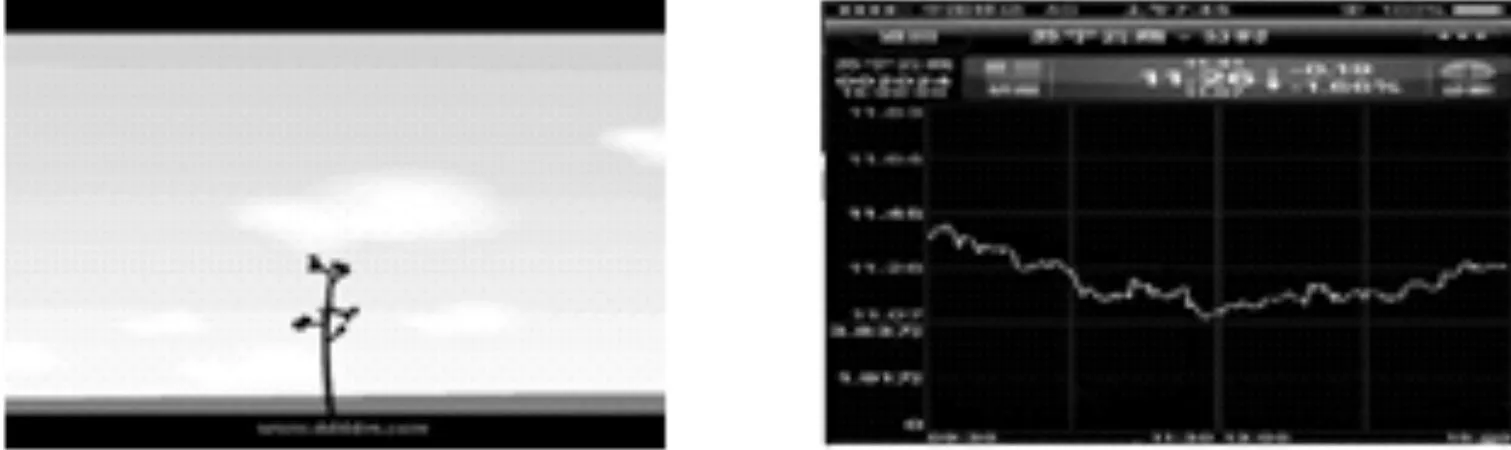
图1
问题2你能举出一些这样的例子吗?
设计意图:创设实际生活中的问题情境,学生初步感受函数的本质,激发学习兴趣,提升学习动力.通过问题2,学生感受到生活中存在大量一个变量随着另一个变量的变化而变化的实例,明确学习函数概念的必要性.
2.2 合作探究,培养毅力与探究力
活动1:十一黄金周期间,小明骑共享单车去黄鹤楼景区,他以0.2 km/min的速度匀速行驶,行驶的路程为skm,行驶的时间为tmin.
问题1请填表1.

表1
问题2速度、路程与时间中,哪些是变量?
问题3这些变量之间有什么关系?可以用一个关系式来描述吗?
设计意图:学生经历填表的过程,初步感受每一个时间t就有一个唯一确定的路程s与之对应.构建有效的“问题链”,将问题聚焦在两个变量之间的关系上,引导学生思考,培养学生的抽象概括能力.
活动2:在景区,小明查询了近5年十一黄金周期间来武汉游玩的人次(如表2).
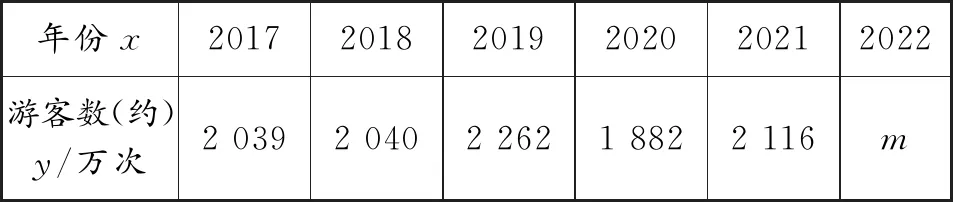
表2
问题1活动2中涉及的量哪些是变量?
问题2这些变量有没有像上面那样的关系式呢?它们之间又有什么关系呢?
问题32022年来武汉游玩的人数m是唯一确定的吗?说说你的理由.
问题4你估计m的值是多少?
设计意图:通过问题链引发学生思考函数概念的本质.m值的估计,不仅加深了学生对“唯一确定”的深刻理解,同时弘扬了伟大的抗疫精神,从而达到数学育人的目的.
活动3:在景区,小明也感受到了十一黄金周期间武汉气温的适宜!下面是景区某天的气温变化图,图2中点的横轴t(单位:时)表示时间,纵轴T(单位:℃)表示气温.

图2
问题1气温变化过程中有几个变量?
问题2时间t与气温T之间又有什么关系呢?你能列出它们之间的关系式吗?
问题36时的温度是多少?
问题410时的温度是多少?22时呢?它们之间有什么关系?
设计意图:通过学生熟悉的气温图,体会在运动变化中当时间t确定时,气温T也随之确定.同时通过问题链,将概念的内涵向纵深发展,体会不同的时间t可能对应相同的气温T.
活动4:请认真观察以上3个活动中相应的运动变化过程.
问题1每个运动变化过程有几个变量?
问题2在同一运动变化过程中,两个变量之间是否具有相同的关系?
设计意图:通过问题链,将思考的核心再次聚焦到函数概念的本质上来,培养学生从实例中提炼、归纳事物共性的能力.
2.3 初步辨析概念,提升辨析能力
活动5:辨析.
问题1观察下列式子,y是x的函数吗?
(1)y=x-1; (2)y=x2;
问题2问题1的式子中,x是y的函数吗?
问题3下列图象中,y不是x的函数的是( ).
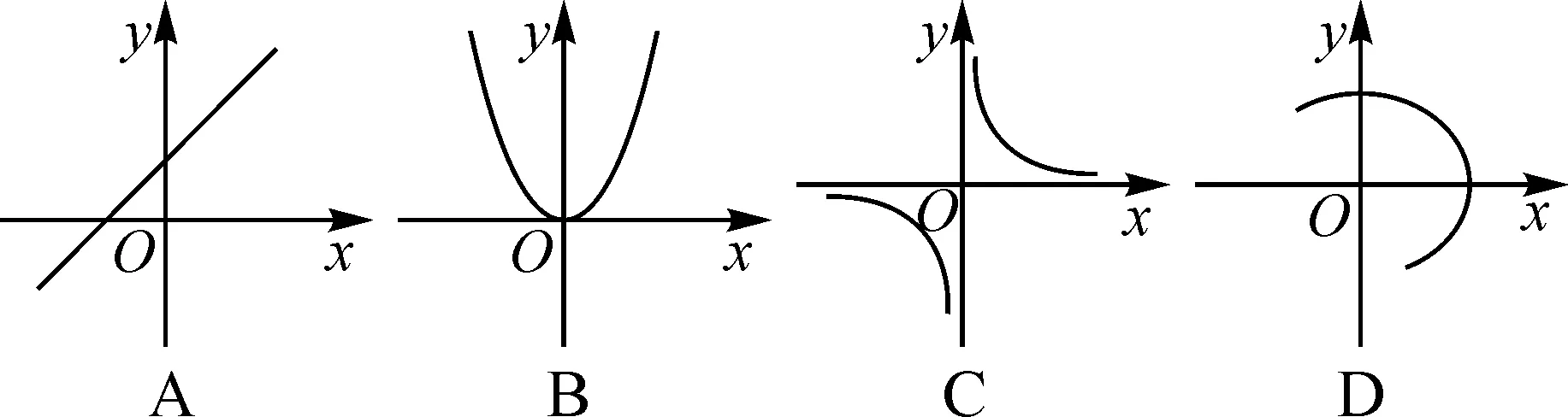
设计意图:通过上述问题链,进一步强化学生对函数概念中“唯一确定”的理解,提升学生的辨析能力.
2.4 综合应用概念,培养创造力
活动6:一辆汽车的油箱中现有汽油50 L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,已知汽车平均耗油量为0.1 L/km.
问题1y是x的函数吗?你能写出y与x之间的关系式吗?
问题2汽车行驶100 km,油箱中还有多少油?
问题3当油箱中的油量还剩20 L时,汽车行驶了多少路程?
问题4汽车最多能行驶的路程是多少?
问题5你能指出自变量x的取值范围吗?那y呢?
问题6从黄鹤楼景区到武当山风景区约有417 km,当油箱中还有10 L汽油时,汽车的油灯就会报警,该汽车在去武当山风景区的途中会报警吗?
设计意图:强化学生对函数概念的理解,引出函数解析式、函数值、最值等概念.问题6引导学生体会数学建模的过程,提升学生分析问题与解决问题的能力.
活动7:请写出下列问题中y关于x的函数解析式,以及自变量x的取值范围.
问题1y是x的0.8倍.
问题2某种原价为x元的商品,按8折出售,现售价为y元.
问题3一个矩形相邻的两边长分别为0.8和x,面积为y.
设计意图:“问题链”让学生明显地意识到同一个函数表达式可以表示不同的意义.同时,强调在求自变量x的取值范围时,需注意它的实际意义.
2.5 归纳概念,培养表达能力
问题1这节课你学习了哪些新的数学概念?
问题2你能用几个关键词概括一下今天所学的内容吗?
问题3如果继续研究函数,将研究哪些内容呢?从什么方向上去研究呢?
设计意图:通过问题链,引导学生提炼本节课所学的数学知识与思想方法,强化“唯一确定”.同时,引导学生发现问题,提出问题,体会函数单元的整体性.
2.6 布置作业(略)
3 教学反思
本节课通过构建有效的问题链,引导学生体会函数概念学习的必要性,函数概念生成的自然性,函数概念理解的深刻性,以及函数概念应用的广泛性,激发学生学习动力,培养学生毅力,提升学生探究能力、辨析能力、创造能力等数学学习力.而就如何设计有效的问题链接这一点,笔者有如下三点思考:
(1)问题链的构建要有关联性.借用小明去黄鹤楼发生的3件事,构建了3组各问之间都有连接的问题链.学生分别从解析式、表格、图象中寻找两个变量之间的本质关系,形成函数概念.
(2)问题链的构建要有生长性.在构建问题链时,台阶跨度要合适,要有梯度和生长性.活动6,让学生的思维呈螺旋式上升,特别是第6个问题,无形中渗透了数学建模、函数与方程,以及多角度分析问题的数学思想方法.
(3)问题链的构建要能激发学生思维碰撞的火花.为有效突出重点、化解难点,应结合相关的内容与学情,围绕函数概念的本质上构建问题链.活动2与活动3中的问题2都是为帮助学生破解函数不一定都要有明显的解析式而仅需“唯一确定”,不同的自变量对应的函数值可以相同等难点.Z

