光学视角下的线段和最值问题解决策略研究*

葛小东 丁永愿 冯润华

⦿ 安徽省合肥市第四十八中学

1 问题提出

线段和的最值问题可以分为以下几类:将军饮马系列,胡不归系列,阿氏圆系列,费马点系列等.这些问题主要考查三角函数、相似三角形、两点之间线段最短、垂线段最短等知识,渗透了对称、旋转、平移等图形变化,是初中几何问题中的难点.这几类问题的解答带有一定的特殊性,当问题推广到更一般的情况时又该如何解决呢?

问题如图1,求mPA+nPB的最小值,其中m≠n,且m与n均为正常数.

图1

2 问题解析

该问题可看作加权将军饮马问题,以学生目前掌握的最值模型是无法解决的.要解决这类问题,我们先了解光的两大原理.

费马原理:光在介质中传播总是选择耗时最少的路径.该原理也被称为“最小时间原理”.

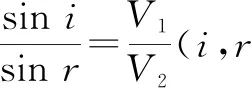
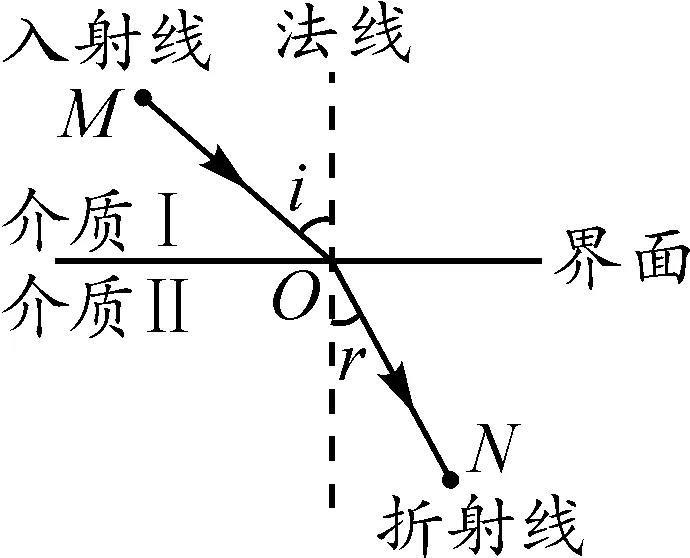
图2

图3

结论1：如图3,动点P在直线l上运动时,在直线外有两定点A,B,过点P作直线l的垂线,当msinα=nsinβ时,mPA+nPB有最小值.

特别指出,当α=β时,图3就是将军饮马模型;当α=90°时,图3就是胡不归模型.

3 推广论证

下面将结论1进行推广,将动点P的轨迹从直线推广至圆.

结论2：如图4,当动点P在圆O上运动时,在圆外有两定点A,B,作射线OP,可得当msinα=nsinβ时,mPA+nPB有最小值.

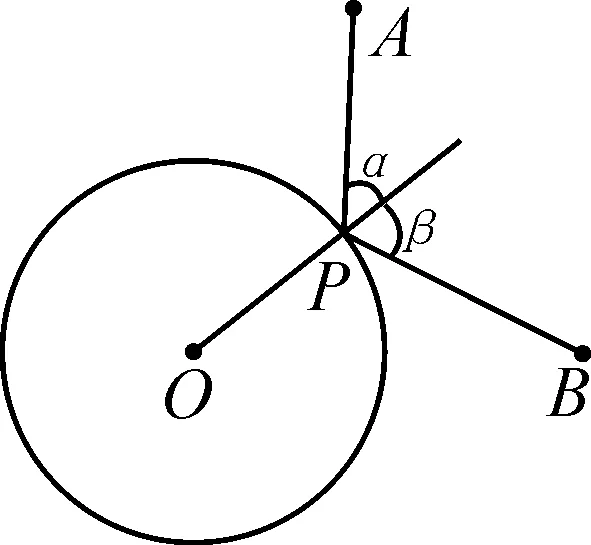
图4

下面将该结论继续推广至加权费马点问题:

在△ABC内找一点P,使得mPA+nPB+kPC最小.(这里m,n,k均为正常数.)

该问题可以通过旋转、相似来解决,这里方法不再展示.下面主要介绍运用结论2解决该问题的方法.

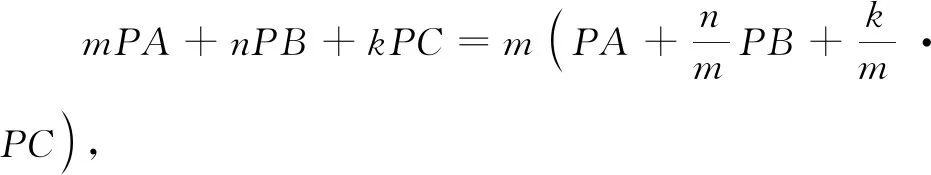
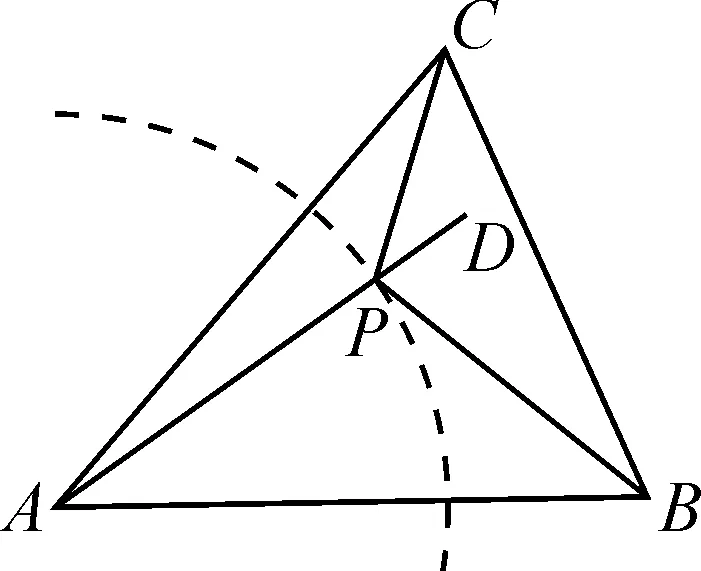
图5

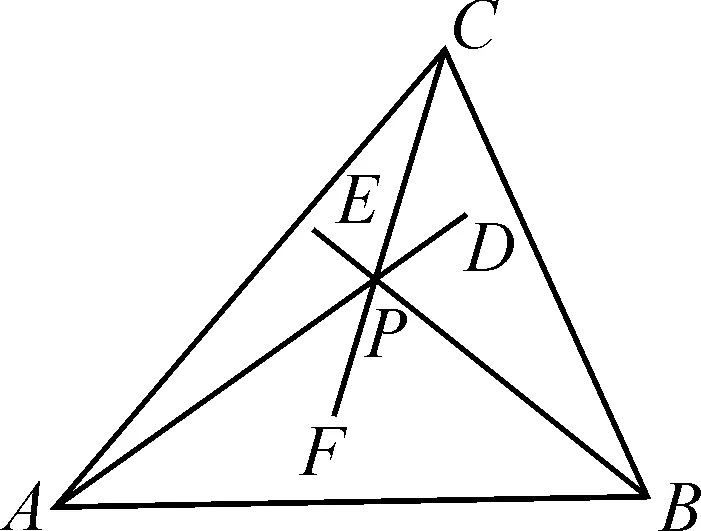
图6

结论3：如图7,在△ABC内存在一点P使得sin ∠BPC∶sin ∠APC∶sin ∠APB=m∶n∶k,则mPA+nPB+kPC有最小值.(其中m,n,k均为正常数.)

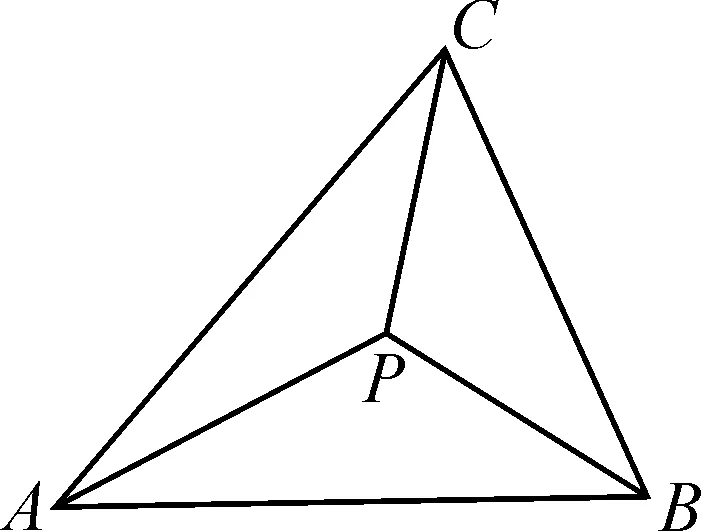
图7

至此,初中常见的线段和的最值问题均运用光学定律完成证明.

4 结论的应用

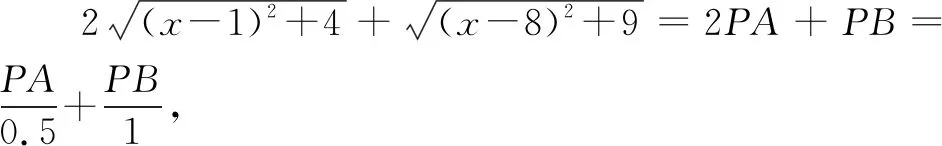
图8

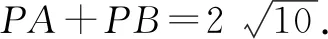
图9

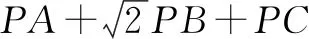
图10

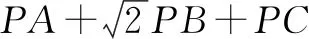
5 结语

5.1 跨学科提高学生对知识的理解

本文中提到的折射定律严格意义上来说是以费马原理为依据,运用求导等数学方法论证得来的,但对于初中生来说,求导论证显然是超纲且困难的,但是将物理结论运用到数学解题中,使得学生对线段和最值的系列问题有了整体的认识.从数学和物理学的角度来说,物理离开了数学几乎寸步难行,而有时候将数学问题转化为物理情景赋予物理意义可轻松解决[1].线段和的最值问题也可以运用位能最小原理解决,线段比值问题可以运用杠杆原理解决,等等.跨学科促使学生建立学科间的联系,帮助学生把所学知识融会贯通,形成对知识的整体性和系统性的认知.提高学生的学习兴趣, 培养学生的创新意识和综合能力.

5.2 跨学科促进教师专业发展

在新课标的理念下,教师不能仅仅专注于数学知识的教学和研究,也要加强对数学学科交叉处综合性较强的知识的理解.跨学科教学可以促进教师不断去学习新的知识和新的教学技能,且能促进学科之间的交流和碰撞,拓展教师的教学视野,促进教师自身的专业发展和综合素质的不断提高.