∠A的度数是多少

◎郭秋妹

星期六早上，阳光明媚。小青通过“小精灵”微信群邀请同学到她家研究数学问题。

大家都准时来到了小青家。小青热情招呼大家后，用电脑“抛出”了题目：

右图中，，点D是AB边上的一点，且DA=DB=BC=CD，求∠A的度数。

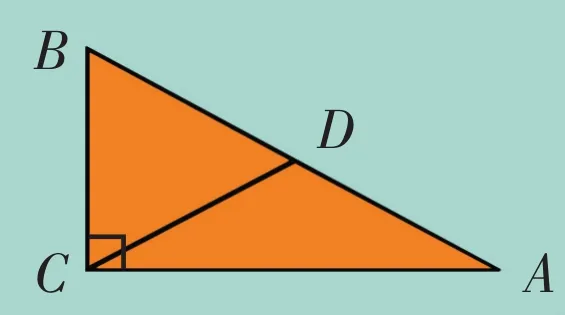
“求∠A的度数，怎么求呢？”小强挠了挠后脑勺，嘀咕着，“图中又没有告诉我们任何一个角的度数。”

小灵拖动着鼠标，将光标在DB、BC、CD三条线段上移动着，自言自语：“DB=BC=CD，三条边相等，说明了三角形BCD……”

“三角形BCD是等边三角形，∠CDB、∠B和∠BCD是三角形BCD的三个内角，它们的大小相等，都是60°。”小军转动着黑溜溜的眼珠，激动地说出了自己的发现。

“因为，所以∠BCA是直角，等于90°，∠B等于60°。”小英停了一下，接着说，“又因为三角形的内角和等于180°，所以∠A=180°-∠BCA-∠B=180°-90°-60°=30°。”

“嗯，除了这种方法外，还有别的方法吗？”小青托着下巴，小小的脸上写满了疑惑。

“因为∠BCA是直角，等于90°，∠BCD等于60°，所以∠DCA等于90°-60°=30°。”小强指着角，微笑着说。

“我知道∠CDA的度数了。”小灵按捺不住内心的喜悦，突然叫了起来。

“小灵，∠CDA是多少度？”大家齐刷刷地把目光集中到小灵的身上，急切地等待着她的回答。

“你们看，∠BDC和∠CDA组成一个平角，平角等于180°。”小灵停顿了两秒，接着说，“∠BDC是等边三角形BCD的一个内角，它的度数是60°，所以∠CDA的度数是180°-60°=120°。”

“在三角形ACD中已经知道了∠DCA和∠CDA的度数，就可以知道∠A的度数。∠A的度数=180°-30°-120°=30°。”小聪发表了自己的想法。

小青甩动着小辫子，脸上两个浅浅的小酒窝显得十分可爱，指着电脑上的图形说：“我们知道了∠DCA等于30°后，就可以知道∠A也是30。”

“为什么？”一向爱打破砂锅问到底的小聪盯着小青，不解地追问着。

“题目告诉我们，DA=CD，说明三角形ACD是等腰三角形，等腰三角形两个底角相等，所以∠DCA=∠A=30°。”

大家听完小青的分析，不停地点头称“是”，并由衷地佩服小青。

一个复杂的数学问题，通过观察、分析，寻找它们之间的内在联系，就可以化繁为简，得到非常完美的解答。

亲爱的小朋友，这道题还有其他简便的算法，你发现了吗？