孔隙对热障涂层微压痕响应影响的数值模拟*

赵伟玲，王 亮，刘 楠，曹枝军，苏怀宇

（1. 中国科学院上海硅酸盐研究所集成计算材料研究中心，上海 201899；2. 中国科学院大学，北京 100049；3.西安理工大学，西安 710048）

热障涂层（Thermal barrier coatings，TBCs）作为一种重要的高温热防护材料，广泛应用于航空发动机及燃气轮机涡轮叶片等高温合金部件上，用于提高发动机热端部件使役温度，延长服役寿命。微纳米压痕技术被视为材料的“指纹”，在表征薄膜和涂层的弹性模量和硬度等力学性能方面起着重要的作用。相比于纳米压痕技术，微压痕技术可以在更大尺度上评价薄膜和涂层的力学性能。

Wang 等[1]采用有限元方法对La2ZrO2（LZ）热障涂层进行了表面微压痕模拟，特别研究了孔隙对大气等离子喷涂热障涂层表面微压痕力学响应的影响，但是所建立的模型为周期阵列几何模型，没有体现出陶瓷层中孔隙随机分布的特征。Qiao 等[2]采用压痕试验得到YSZ 热障涂层的硬度、弹性模量等力学性能，并通过有限元方法深入分析了涂层的应力分布，在计算时只考虑了陶瓷层。Kaneko 等[3]在研究中通过压痕试验的有限元模拟得出多孔热障涂层的弹性模量。热障涂层在制备过程中会不可避免地产生孔隙，且涂层在恶劣的工作环境下也非常容易产生裂纹缺陷，因此研究微压痕下孔隙和裂纹的相互作用对研究热障涂层的真实结构及实际服役状态下的失效机制具有重要意义。

国内外的压痕试验模拟主要集中在简单结构或含简单分布孔隙热障涂层的力学性能上，亟待建立更加能反映热障涂层几何结构的模型。因此，本文通过Python二次开发的方法在ABAQUS 中建立了含随机孔隙的热障涂层模型，并研究了不同孔隙率对压痕响应的影响。又利用XFEM 法模拟了微纳米压痕试验过程陶瓷层内的裂纹扩展，通过建立两种模型来探究微裂纹和孔隙间的相互影响，以及涂层内裂纹萌生扩展的规律。

1 带随机分布孔隙的热障涂层的数值模型建立

1.1 随机孔隙模型开发

本研究选取等离子喷涂工艺制备的热障涂层，在热障涂层制备的过程中，涂层中会产生孔隙等缺陷，陶瓷层孔隙率f 一般在4%～20%之间[4]。孔隙的存在一方面会成为裂纹萌生的源头，导致涂层过早失效；另一方面会增加热流传递的阻力，从而降低涂层的有效热导率。因此，本模拟工作中将热障涂层中的孔隙简化为圆形孔洞，建立含随机分布的圆形孔洞的热障涂层模型，用于模拟微压痕下随机空间位置分布的孔隙及不同孔隙率对热障涂层的动态弹塑性力学行为响应。

图1 为建立含孔隙材料有限元模型的流程图。通过该流程图建立含不同孔隙率的圆形孔隙随机分布的热障涂层模型，主要分析孔隙率对微压痕下涂层动态响应的影响。

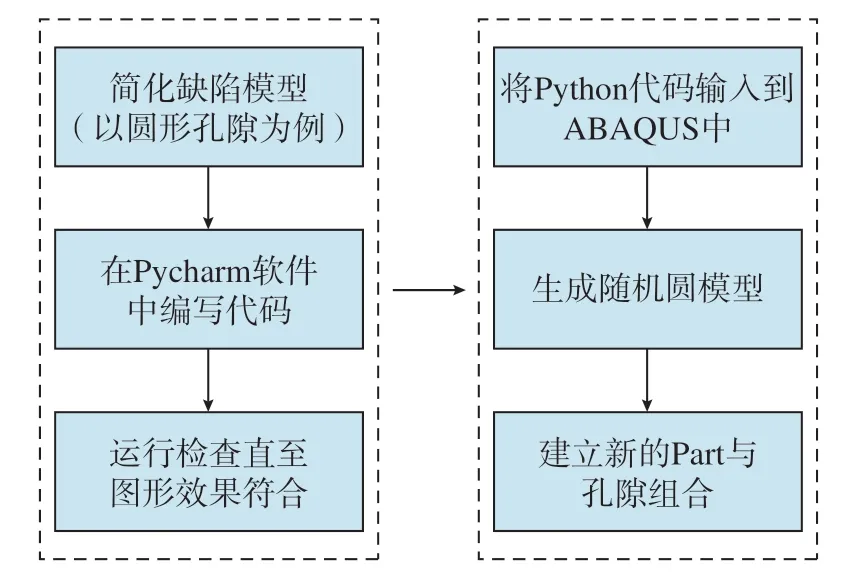
图1 建立含孔隙材料有限元模型流程图Fig.1 Flow chart for building a finite element model of a material containing pores

使用Python 二次开发集成开发环境并利用Pycharm软件编写代码，进行随机圆的二维模型构建，具体步骤如下： （1）首先在ABAQUS 中建立一个2D 的随机圆形模型，并在工作目录下的rpy 文件中找到生成单个圆形的代码，基于单个圆形模型的代码来生成多个圆； （2）然后在ABAQUS软件中引入相应的Python库，便于Python调用；（3）进一步定义随机圆的投放区域； （4）再根据设定的孔隙率计算出需要的随机圆的个数，对随机数x（圆心横坐标）、y（圆心纵坐标）、r（半径）进行初始化，并通过随机函数赋值，使圆形可以随机分布在投放区域中；（5）随后进行相交判断，目的是使各个圆不相交，即定义两圆圆心与圆心的距离大于两圆的半径之和； （6）最后基于ABAQUS 中单个圆形的rpy 文件编写圆形模型的代码； （7）在ABAQUS 的图形用户界面输入Python代码，运行查看随机分布圆的模型，以此判断程序编写是否无误及模型是否合理。并且因为Python 编码中包含随机函数，所以运行后得到的随机圆模型有多种结果，其分布并不相同。在得到的某些模型中，部分随机圆可能会分布在靠近涂层边缘的地方（在ABAQUS前处理中也可以做移动操作，再判断是否发生干涉），若此时导入到ABAQUS 中计算，可能会使计算结果不收敛，因此可以多运行几次程序，直至建立相对最合适的模型。得到的含随机圆形孔隙的模型如图2 所示。

图2 含随机圆形孔隙的模型Fig.2 Model with random circular pores

1.2 模型描述及材料属性

在ABAQUS 中建立热障涂层模型与随机圆进行布尔操作，从而得到含随机孔隙的热障涂层压痕模型，如图3 所示。其中，涂层从下往上分别为DZ125 镍基高温合金基体、NiCoCrAlY 粘结层、质量分数8% Y2O3部分稳定ZrO2（8YSZ）陶瓷层。基体和涂层中各层的性能参数如表1 所示[5–7]。在整个模拟过程中做出以下假设[8]：（ 1）8YSZ 层材料被认为是线弹性的，而基体和粘结层均包含弹性/塑性响应。假设Von-Mises 屈服准则和双线性运动硬化用来描述基体和粘结层的应变硬化行为。（ 2）虽然涂层在沉积方向和界面方向的性能不同，但孔隙、裂纹等微观缺陷没有明显的方向性，排列不规则，涂层组织不均匀。因此，不同方向的力学性能几乎没有差异，在当前的模拟中，涂层可以被视为具有各向同性。基体也具有各向同性的，因此为多晶材料。并假设所有材料都与温度无关。（ 3）由于微压痕试验是在室温条件下进行的，所以模型中不考虑蠕变和氧化行为。（ 4）界面为平直的，没有考虑界面的起伏。

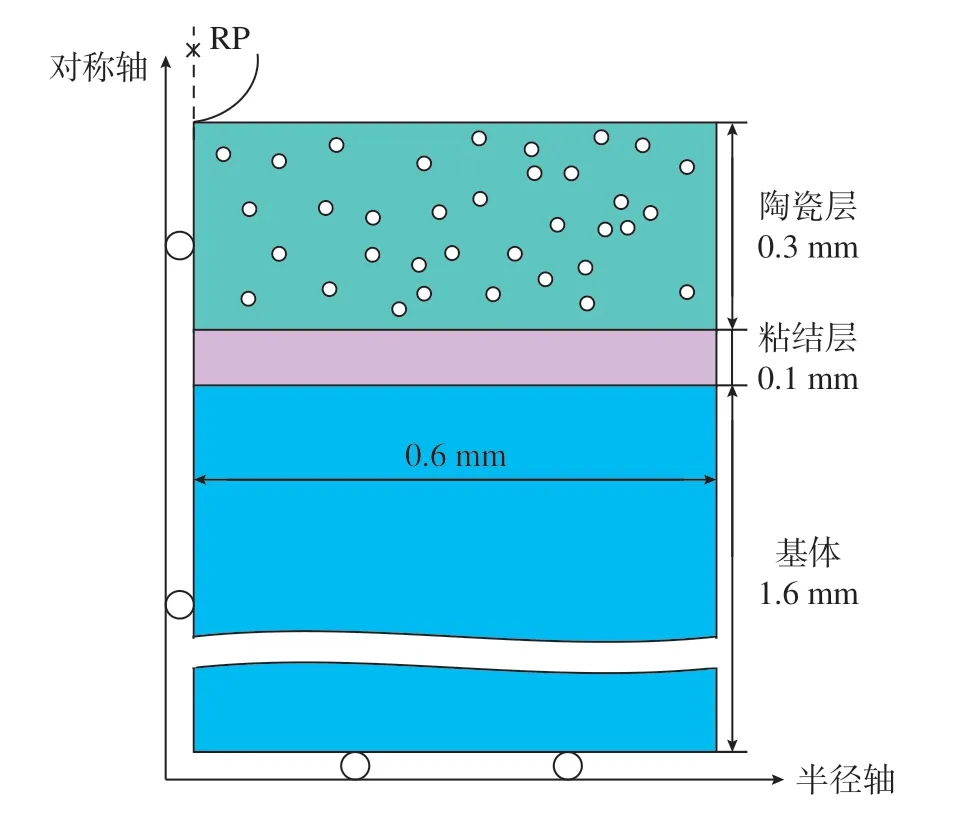
图3 热障涂层压痕模型示意图Fig.3 Schematic illustration of the indentation model for TBCs

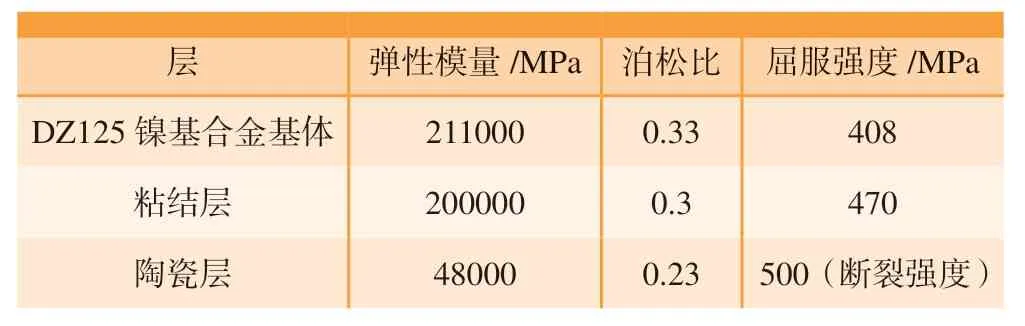
表1 基体和涂层各层的性能参数[5–7]Table 1 Performance parameters of substrate and each layer of coatings[5–7]

在模拟中基体厚度1.6 mm、粘结层厚度0.1 mm、陶瓷层厚度0.3 mm、孔隙半径8 μm、孔隙率5%、圆柱试样半径0.6 mm、半球形压头半径0.2 mm、压入深度0.03 mm。

在ABAQUS 中进行微纳米压痕试验的模拟一共要建立两个部件：压头和热障涂层。压头材料一般选择金刚石材质，其弹性模量为1060 GPa，泊松比为0.07。由于压头的弹性模量比热障涂层高出很多，所以在ABAQUS 建模过程中可以将压头看作理想的刚体，从而有效减少作业计算的时间，提高计算效率，且对模拟计算结果无大的影响。有限元网格的划分要考虑到接触的区域，网格划分采用四边形四节点减缩积分单元，并对靠近压头尖端的地方、接触区域下方及孔隙周围网格进行细化处理。此外，实际的压痕试验过程中大多时候加载速度比较慢，所以可以看成是一个准静态的加载过程[9]。

1.3 扩展有限元法模拟裂纹扩展

上述方法虽然在一定程度上可以模拟压头作用在含孔隙的热障涂层的微压痕响应的过程，但是还存在一定的局限性，孔隙在被压实后发生了严重的扭曲变形，相关单元失效，无法探究裂纹的产生与扩展。在上述模型的基础上，进一步采用扩展有限元法（XFEM）来模拟微纳米压痕试验过程陶瓷层内的裂纹扩展。采用基于牵引–分离（Traction-separation）描述的双线性本构模型[10]，如图4 所示，其中横坐标δ 表示整个过程中材料产生的变形量，纵坐标σ 表示最大主应力。当材料受到的最大主应力到达最高点2 时发生损伤，之后材料沿下降曲线2–3–4 发生演化；当材料的变形量δ 到达δmax时，上升段直线0–1–2 与横坐标形成的面积等于临界释放率，材料被破坏。该模型需要定义两个关键准则。

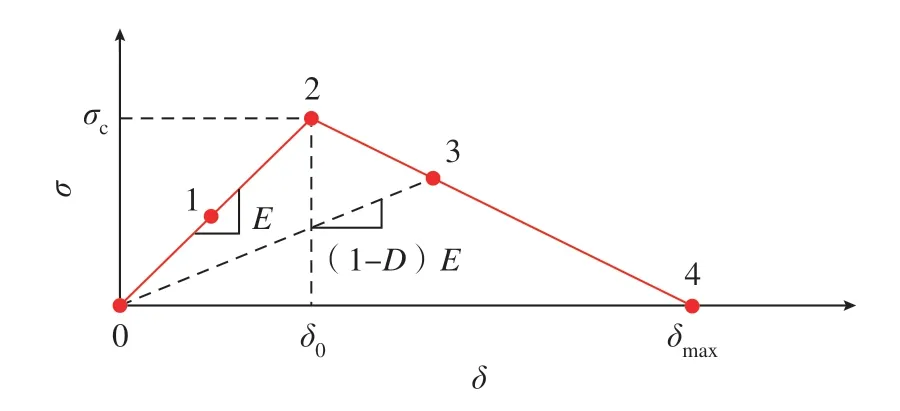
图4 双线性本构模型Fig.4 Bilinear constitutive model

损伤起始（Damage initiation）选择最大主应力准则（式（1））。

式中，σn为法向应力；σs为剪切应力；为名义应力的峰值。

损伤演化（Damage evolution）为基于能量的线性软化准则（式（2））。

式中，Gn、Gs分别为法向、剪切方向能量释放率；Gnc、Gsc分别为法向、剪切方向临界能量释放率。

本模型中取临界最大主应力为150 MPa，即当材料受到的最大主应力值达到150 MPa 时，材料发生损伤；临界断裂能量释放率为40 J/m2[11]。

等离子喷涂8YSZ 热障涂层的孔径分布服从对数正态分布，陶瓷层内孔径大小主要集中在1～10 μm 之间。由于热障涂层在等离子喷涂制备过程中会生成平行界面的裂纹，且在分段的大气等离子喷涂热障涂层的制备过程中在喷涂态的热障涂层表面预制竖直裂纹，因此通过建立以下4 种模型来探究微裂纹和孔隙间的相互作用，并研究涂层内裂纹萌生扩展的规律。模型1 在不含孔隙的热障涂层8YSZ 层表面0.1 mm 下预制一条长为50 μm 平行于界面的直线裂纹；模型2 在含随机分布圆形孔隙的热障涂层8YSZ 层表面0.1 mm 下预制一条长为50 μm 平行于界面的直线裂纹；模型3 在不含随机分布圆形孔隙的热障涂层8YSZ 层表面预制一条长50 μm、距离对称轴0.1 mm且平行于对称轴的竖直裂纹；模型4 在含随机分布圆形孔隙的热障涂层8YSZ 层表面预制一条长为50 μm、距离对称轴0.1 mm 且平行于对称轴的竖直裂纹。

2 数值计算结果与分析

2.1 孔隙的影响

为了探究孔隙率对压痕响应的影响规律，控制孔隙率半径大小为8 μm，研究了孔隙率分别为0、5%和9%情况下热障涂层压痕下的弹性塑形力学响应行为。

图5 为不同孔隙率的Von-Mises 应力分布图。通过对比可以看出，在最大载荷下，具有孔隙的热障涂层发生塑性变形区域的面积小于无孔隙的热障涂层。压头与涂层表面相互作用界面下的接触区域发生塑性变形，塑性变形同样出现在压头附近孔隙的周围。通过比较图5（c）和（d）可以看出，卸载后，只有孔隙附近或靠近孔隙的区域以及靠近压头位置的涂层表面以下区域保持塑性变形。图5（c）和（d）均显示了孔隙存在时应力分布的不连续性，且该区域在计算时容易出现应力集中。在压头的作用下，最大载荷时，靠近压头接触的附近区域孔隙形状发生了变形或者弥合；卸载后，由于孔隙的存在会释放一定的应力集中，可以看到部分的孔隙变形发生了恢复，且孔隙周围的应力分布也有所变化。

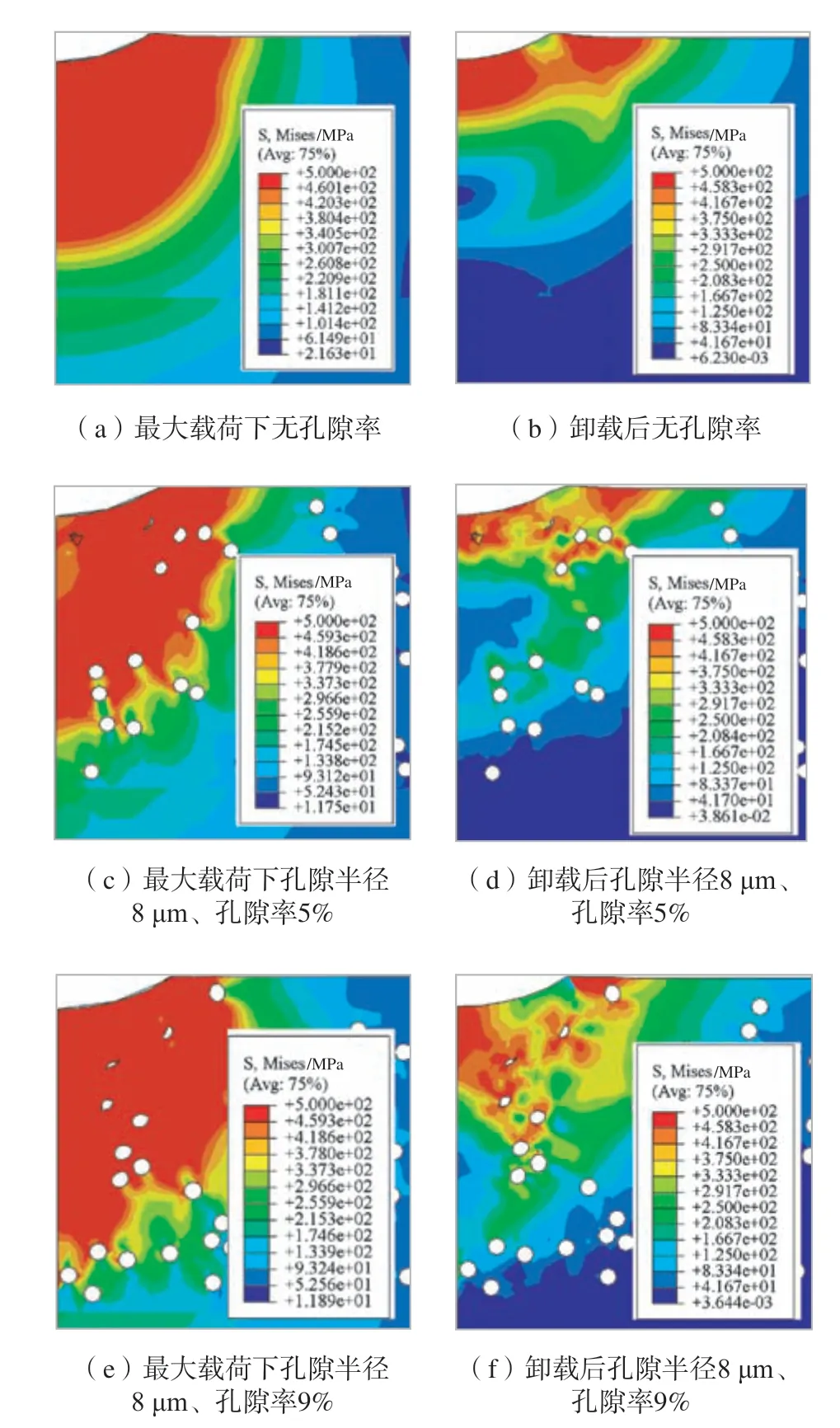
图5 不同孔隙率的热障涂层Von-Mises 应力的分布Fig.5 Distribution of Von-Mises stresses in thermal barrier coatings with different porosity

图6 为不同孔隙率热障涂层S11的分布图。S11代表沿x 轴的正应力，可以看出，在最大载荷时压应力位于压头与热障涂层相互作用区域的下方及孔隙的周围；卸载时，最大压应力位于压头与热障涂层相互作用区域的下方、孔隙的周围及靠近Pile up 位置的涂层区域。对比图6（a）和（e）可知，最大压应力位于孔隙周围，对比最大载荷时和卸载后发现，随着孔隙率的增加，对应的压应力区域的面积增大。

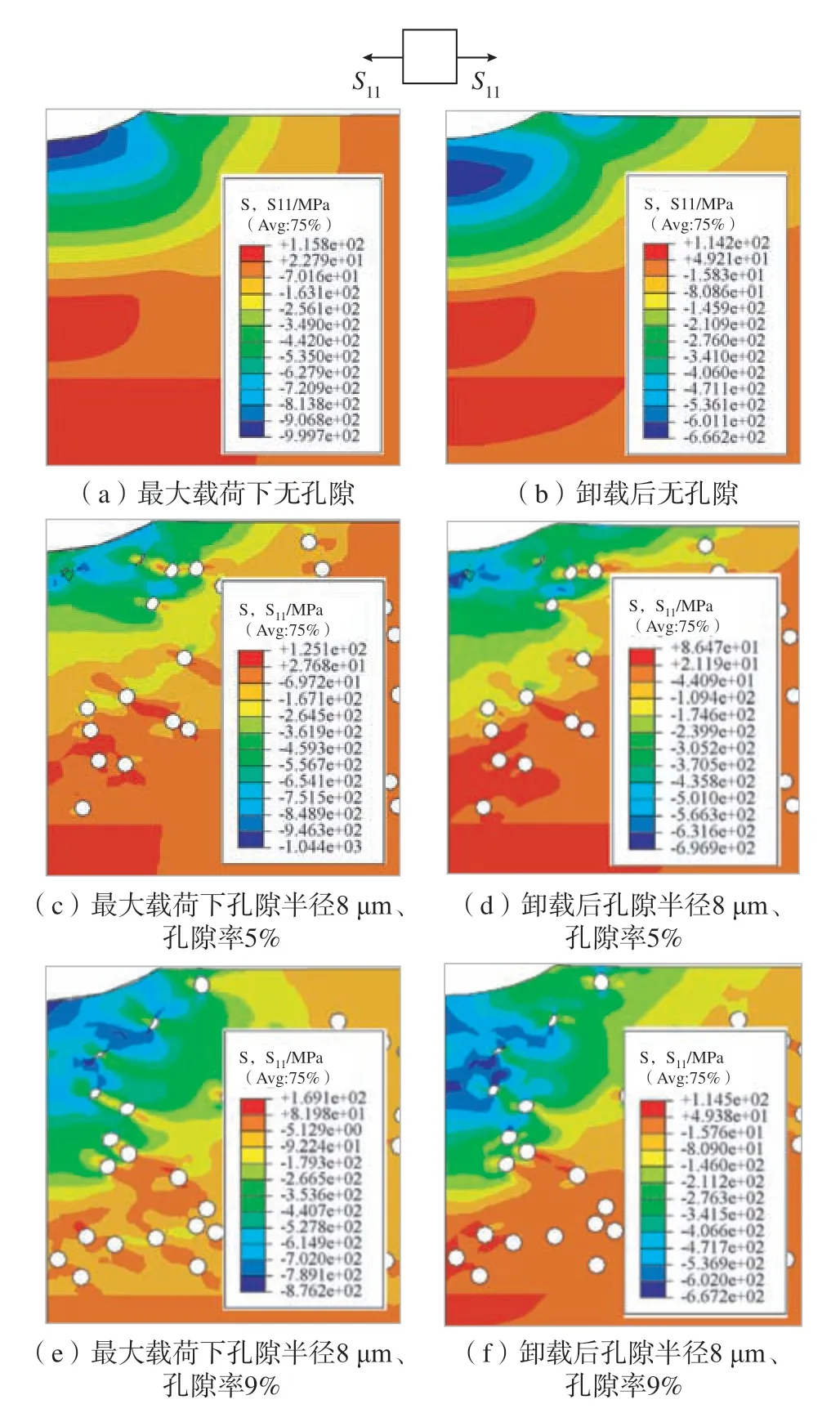
图6 不同孔隙率的热障涂层S11 的分布Fig.6 Distribution of S11 in thermal barrier coatings with different porosity

图7 为不同孔隙率热障涂层S22的分布图。S22代表沿y 轴的的正应力，由图7（a）和（c）可以看出，最大压应力区域的面积变宽，最大拉应力位于孔隙附近，更靠近接触面。通过对比图7（b）、（d）和（f）可知，孔隙的存在导致应力释放，最大拉应力区域有所缩小，且孔隙率越大，最大压应力区域应该越小。

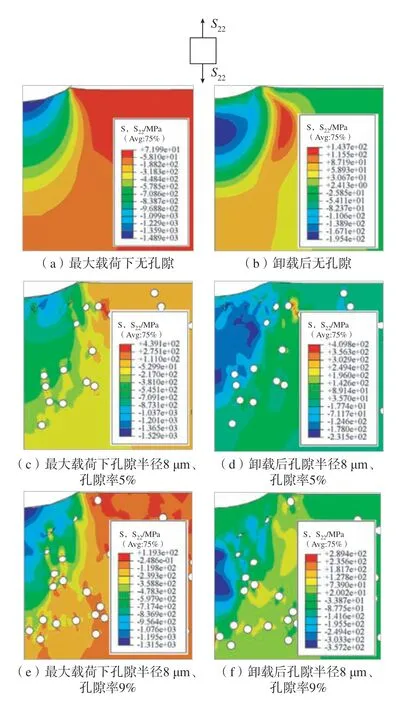
图7 不同孔隙率的热障涂层S22 的分布Fig.7 Distribution of S22 in thermal barrier coatings with different porosity

图8 为不同孔隙率热障涂层的载荷–位移曲线。可以看出，在相同的压入深度0.03 mm 下，载荷–位移曲线具有相似的趋势。无孔隙热障涂层的最大载荷比有孔隙热障涂层的最大载荷高。同样，无孔隙热障涂层的弹性恢复位移比有孔隙热障涂层的弹性恢复位移大。将无孔隙热障涂层的载荷–位移与有孔隙热障涂层的载荷–位移曲线进行比较，可以看出，在加载的初始阶段，载荷–位移曲线的上升几乎一致。之后有孔隙热障涂层的加载曲线开始偏离，低于无孔隙热障涂层的加载曲线。这种现象可以解释为，当陶瓷层含一定量孔隙时，认为陶瓷层的有效弹性模量降低，因此在塑性变形阶段加载曲线的斜率减小，含孔隙热障涂层的加载曲线不表现为普通材料的典型加载曲线。对比两种孔隙率的载荷–位移曲线可以看出，随着孔隙率的降低，载荷–位移曲线与无孔隙时的载荷–位移曲线趋于接近。

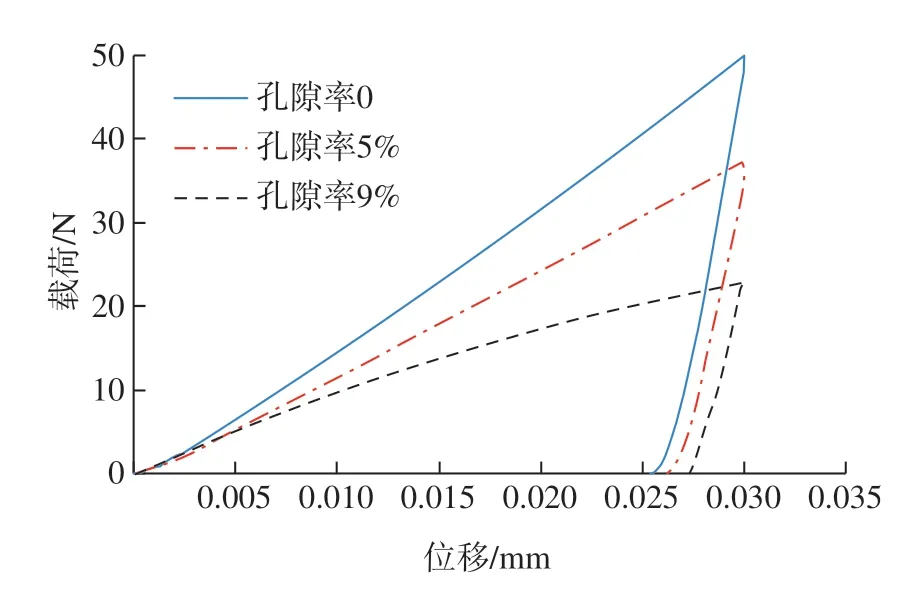
图8 3 种不同孔隙率热障涂层的载荷–位移曲线Fig.8 Load-displacement curves for TBCs with three different porosities

对于含有一定孔隙率的热障涂层，其有效弹性模量与无孔隙热障涂层的弹性模量满足式（3）[12]。

式中，E 为涂层的有效弹性模量；E0为无孔隙涂层的弹性模量；B 为与孔隙率无关的常数；P 为涂层的孔隙率，%。

从式（3）中可以看出，孔隙率会影响热障涂层的有效弹性模量，并且随着孔隙率的增大，涂层的有效弹性模量减小。这与图8 中的3 种不同孔隙率热障涂层的载荷– 位移曲线所反映的趋势是一致的。

2.2 横向裂纹和竖直裂纹扩展模拟结果

图9（a）和（b）为热障涂层内陶瓷层横向微裂纹扩展模拟结果，图9（c）和（d）为涂层内陶瓷层竖直微裂纹扩展模拟结果。其中，a 为预制微裂纹长度，Δa 为裂纹扩展长度。图9 给出的是S22计算云图，即y 方向应力云图，可以看出，靠近压头的地方存在较大的压应力集中，远离压头的地方主要是拉应力。孔隙密集处孔隙能够一定程度上释放应力集中，且孔隙附近同时存在拉应力和压应力，且裂纹扩展的方向朝向拉应力较大区域方向，孔隙的尖端存在应力集中，孔隙能够钝化这种应力集中，并改变裂纹的扩展方向，使得孔隙表现出对裂纹的“吸引”或“俘获”效应，使裂纹扩展方向发生偏折。从图9（a）可以看出，横向裂纹在y 方向应力的作用下向右下方扩展，同时微裂纹会偏转向强度比较弱的地方。在这一过程中，微裂纹会同时出现张开（Ⅰ型）和错动（Ⅱ型）扩展。从图9（c）可以看出，涂层表面的竖直裂纹一开始沿着竖直方向继续扩展，到达孔隙处后，裂纹向孔隙的方向偏移扩展。综合对比图9 可以得出以下结论。

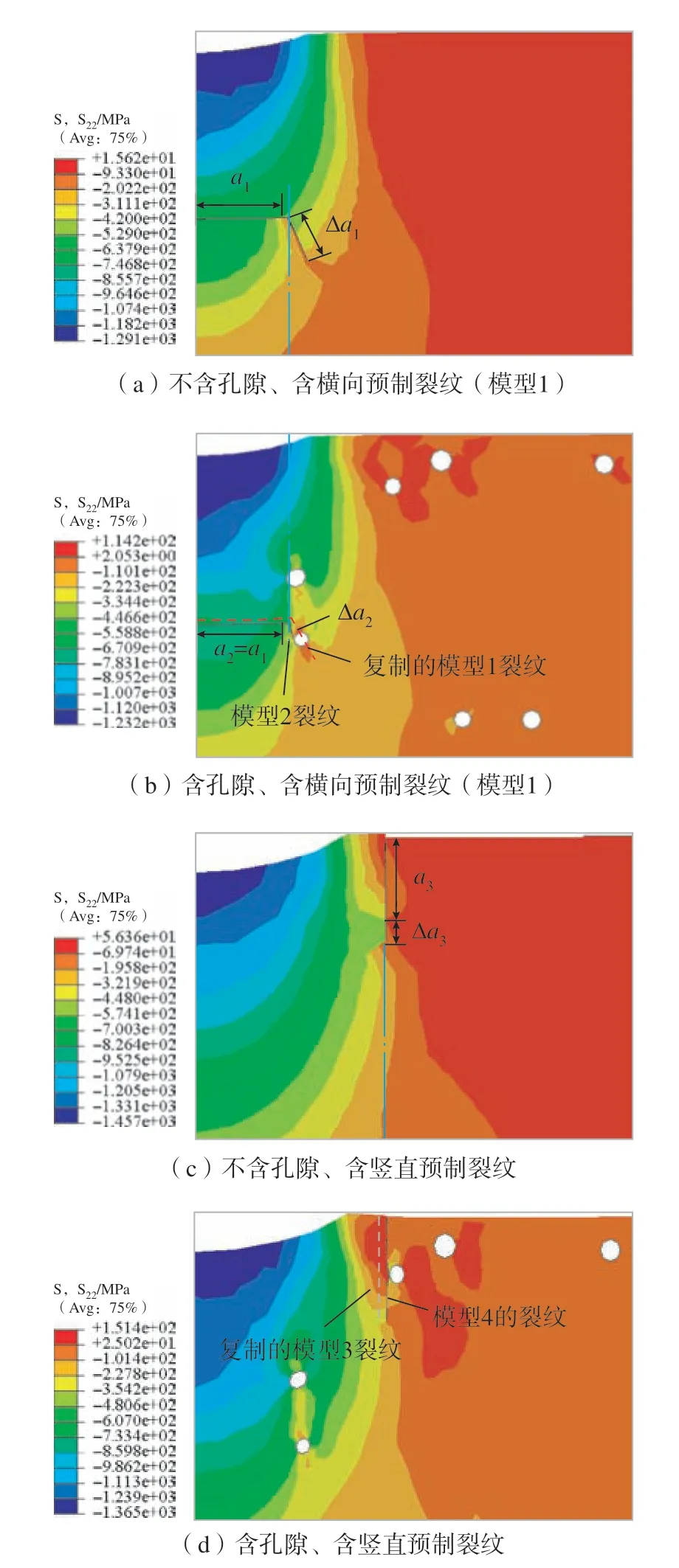
图9 热障涂层内陶瓷层横向和竖直微裂纹扩展云图Fig.9 Contour plot of stress of transverse and vertical micro-crack propagation in the ceramic layer within the thermal barrier coating

（1）孔隙会“吸引”裂纹。微裂纹会偏转向强度比较弱的地方，从图9（b）可以看出，由于孔隙的存在，裂纹向孔隙的方向偏移扩展，图9（d）中也反映出了相应规律。

（2）孔隙会在一定程度上阻止裂纹扩展。图9（a）和（b）中Δa1>Δa2，这是由于圆形孔隙的存在会使裂纹尖端的应力集中系数大幅度降低，从而导致裂纹停止扩展，即裂纹扩展到孔隙所在的位置时不会穿透孔隙继续扩展。

3 结论

本文采用有限元模拟计算了含随机分布的圆形孔隙的等离子喷涂热障涂层的微纳米压痕响应行为。并利用XFEM 模拟分析了微纳米压痕试验过程陶瓷层内的裂纹扩展，探究微裂纹和孔隙间的相互影响，以及涂层内裂纹萌生扩展的规律，得出如下结论。

（1）陶瓷涂层中存在的孔隙会在加载和卸载过程中释放一定的应力集中，从而改变涂层应力的分布特征。

（2）在相同压痕深度下，无孔隙热障涂层的最大载荷比有孔隙热障涂层的最大载荷高。卸载过程中无孔隙热障涂层的弹性恢复位移比有孔隙热障涂层的弹性恢复位移大。

（3）陶瓷层中孔隙的存在会导致裂纹向孔隙的方向偏移扩展，并在一定程度上阻止裂纹扩展。