建构从“说理”到“推理”的数学课堂

张海生

【摘要】数学说理，是发展小学生推理能力的应然之路，建构小学数学说理课堂是当代一线教师研究的新领域.文章以五年级上册第六单元“组合图形的面积”为例，提出了建构从说理走向推理的数学课堂的途径：问题引领、活动笃行、习题明辨，让学生拥有自主的推理空间，建构自己能接受的推理方法，尤其在思考、探索、推理的过程中促进推理能力的发展.

【关键词】小学数学；说理；推理；数学课堂

“双减”背景下，建构“提质增效”的数学课堂是当今一线数学教育工作者迫在眉睫且又不可回避的重任.笔者研析“双减”政策发现，“双减”减的是学生过重的负担，增的是学生的学科素养；减的是教师的喋喋不休、题海卷山，增的是学生的幸福指数，而数学说理是一种运用数学语言进行逻辑表达的过程，该过程对小学生数学思维能力的发展有着深远且直观的影响，因而建构小学数学说理课堂，既能满足落实“减负不减质”的要求，又能够促成小学生推理能力发展的落“堂”生根.

一、问题引领，留足推理空间

诸多研究表明，说理区别于传统课堂上的简单问答，教师要立足学生知识认知与实际操作的发展水平，致力于学生独立思考分析、合作讨论判断，让学生在思考、分析、讨论的过程中进行合理的判断，进而得出结论.减负的初衷是减轻作业负担，让学生朝着德、智、体、美、劳全面发展，课堂提问为引导学生自主探索、促成学生深度思考而提出，让学生思维从“低阶”发展为“高阶”，这与数学说理课堂的目标不谋而合.因而在小学数学说理课堂上，教师要以教学内容、学生学情需求、学生思维特征为依据设置进阶式问题串，以问题驱动学生积极思考、深入探究，尤其为学生的“探”与“思”留足空间，使学生历经观察、判断、验证等活动，展示自我的个性化思维，为每名学生推理能力的发展提供脚手架.

例如，在教学“求组合图形面积”时，教师可以通过环环相扣的问题串，驱动学生观察组合图形，从组合图形的特征入手通过辅助线将组合图形分解为已学的基本图形，如三角形、长方形、平行四边形等.

估一估：如图1，观察“山”字图，估算“山”图的面积约为多少？

想一想：“山”图内是否含有学过的基本图形，如三角形、长方形等.

画一画：用辅助线，将组合图形转化为基本图形.

算一算：结合自己的思考过程，计算“山”图的面积.

上述四个问题，既提供了推理能力培养的前提与条件———认知疑惑，又指明了符合学生逻辑思维需求的探索方向，留出充足的自主推理的空间，很大程度上确保数学说理课堂的效果.具体为：“估一估”，学生直观地看到“山”图与之前学过基本图形之间的“异”，让学生直观地认识到“山”图面积可以转化为三角形面积，产生探索“山”图与三角形之间关联性的欲望；“想一想”，肯定了学生的直观判断———转化，同时明确将组合图形分解为常见基本图形的转化基础方向；“画一画”，鼓励学生动手操作，通过多元化途径获取信息、寻找证据，进行有理有据的推理，让学生“有话说”且有理有据地“说”，同时加强学生之间的交流探讨，引领学生再度审视自己独立思考所得，进行适切的重构、抉择；“算一算”，引领学生自觉地以图中的15米、13米、8.5米及4米为依据进行分析，且有意识地关联之前学过的梯形面积S=（a+b）×h÷2、三角形面积S=a×h÷2、长方形面积S=a×b等，进而将组合图形转化为基本图形进行计算.这样的过程中，既能够让学生“看”到求“组合图形的面积”方法的多样性、其他同学身上的“闪光点”和差异性，又能够促使学生形成获取、处理信息的能力，使学生进行有理有據的判断、验证、批判，为推理能力培养、发展提供基础.

二、活动笃行，建构推理方法

在数学教学中，教师可以结合小学生“爱玩”“爱动”“感性决定理性”等特征，并在明确“说理”“推理”“思维”三者之间关联的基础上，有意识地组织、开展、挖掘、利用“说理”活动，让推理能力浸润“说理”活动，使学生体会到推理的作用与价值.在说理课堂上，教师依据推理能力的本质———有理有据的思考，有条不紊地表达组织开展课堂活动，让思维从“不可视”转为“可视”，语言从“粗略”转向为“精准”，最终使学生建构自己能接受的推理方法.如，“组合图形的面积”的说理课堂上，教师围绕“思维，如何可视？”“语言，何以精准？”这核心问题，组织开展了“算法争霸赛”.该争霸赛分为“用线分图”与“以理服人”两部分，具体如下：

（一）用线分图———画辅助线，将组合图形分为基本图形

这里提到的“用线分图”是一种以学生为主体的实践活动，从本质上来讲，它也是较为复杂的认知活动.该活动就是“说理”课堂上常见的“直观”说理，意在让思维从“不可视”转化为“可视”.活动中，教师提出“用辅助线将‘山图形转化为基本图形，哪位同学知道如何画？”这一问题，让学生画出自己能想到的所有分解方法，利用“所有”二字，引导学生多维度分析、设想、验证，助力学生打破思维定式，使学生亲身体会到求“组合图形的面积”方法的多样性，明确求“组合图形的面积”的关键———将组合图形拆分为基本图形.接着，教师可利用多媒体技术展示“山”图形的拆分类型，让学生有意识地联系动手操作的过程，通过适切的辅助线，将自己脑海深处的想法“显现”出来，让独立思考的过程从“不可视”转化为“可视”，一方面让学生直观地看到陌生的组合图形转变为熟悉的基本图形，满足小学阶段学生思维发展特性的同时，也能够减少学生抽象理解的困难，另一方面由于组合图形“变身”过程是由学生主导的，他们历经分析、思考、批判、再次建构等过程，加强了对知识的理解内化.

（二）以理服人———自由择法，说一说想法的思维过程

这里提到的“以理服人”，可以视为日常数学课堂的互动交流环节，它作为“说理”活动的重要组成部分，旨在让学生在“交流”说理的过程中学会用有理、有据、有逻辑的语言表达自己的推理过程，一定程度上强化推理的逻辑性.活动中，教师提出“计算‘山图形的面积，你会选用何种方法？说一说想法.”这一问题，驱动学生的思考方向从“如何做”转向为“为何做”“何以做”，同时点拨学生尽可能利用语文学科中掌握的关联性词语：如果……那么……、只要……就……、因为……所以……等，使学生在交流、探索中找到语言表达的努力方向———有理有据、有条不紊.接着，教师可让学生就自我选定的算法，说一说心中的想法，具体为：

学生A：我选择用（8.5+15）×13÷2-8.5×4÷2计算.想法就是只要先把梯形添补完整（如图①），再去掉空白的三角形就是“山”图形的面积；

学生B：我选用8.5×13÷2-8.5×4÷2+15×13÷2计算.如果将“山”图形分成三个三角形（如图②），那么“山”图形的面积可以用8.5×13÷2-8.5×4÷2+15×13÷2来计算.

学生C：我选用8.5×13-8.5×4÷2+（15-8.5）×13÷2计算.如果将“山”图形分成左为平行四边形、右为三角形（如图③），那么“山”图形的面积可以用“平行四边形-空白三角形+右边三角形”计算.

学生D：我选用8.5×13-8.5×4÷2+（15-8.5）×13÷2计算.因为该方法是长方形的面积计算公式，所以把“山”图形添补为梯形后，从梯形短边的两顶点做垂线，建构一个长方形，再将左、右两边的三角形割补形成一个底边为（15-8.5）、高为13的三角形（如图④）.

学生E：我选用15×13-8.5×4÷2-（15-8.5）×13÷2计算.想法就是只要将“山”图形添補成长为15，高为13的平行四边形（如图⑤），在依次剪去空白的两个三角形的面积，就是“山”图形的面积.

通过上述解读，学生掌握了求“组合图形的面积”的重要方法———分割、添补，不知不觉地提高了用文字语言精准表达推理过程的能力.“交流”说理中，教师立足小学生的逻辑思维习惯，引领学生从“这是怎么想的”走向“为何可以这样想”，彰显出猜想与验证的求证环节，使学生逐步建构自己能接受的数学推理方式.

三、习题明辨，发展推理能力

习题的主要功能体现在检查学情、巩固知识、拓展应用、诊断学情四个方面，而诸多研究表明，其也是让学生学会独立思考、独立判断的载体，尤其在“双减”政策下，教师理当杜绝“题海卷山”，为学生提供自由成长的“内驱力”———推理能力.在说理课堂上，教师要贯彻“减负增质”“因材设题”“培优补差”的理念，针对生生之间的差异性进行新知学习之后的深度思考与批判重构，让推理能力切实发展.如在“组合图形的面积”的说理课堂上，教师围绕“如何累积推理经验？”“何以融通推理方法”，设置了“巩固基础”与“拓展训练”两大类型的习题，具体如下：

（一）巩固基础———举一反三，累积推理经验

教材内“练一练”第1道题的第（1）小题“估一估，这面中队旗的面积大约有多大？与同伴交流你的想法.”有助于强化学生对新知识的认知与掌握，但却因推理空间不足、推理方法的单一，导致学生的思维趋向于定式，更不利于学生推理能力的发展.为此，课堂上教师呈现出的习题则是由“一面中队队旗的面积是多少？”改编而来，具体为：

2022年是中国少年先锋队建队73周年，学校举办实践活动———“做中队队旗”.五（1）班准备做的中队队旗（图3），负责采购红布的小美、亮亮、北极、萱萱和博艺分别用自己数学推理方式，计算了中队队旗所需的红布面积.如果你是队旗制作的总负责人，你认为他们五人的方法正确吗？请说明理由.

小美的方法：80×60-60×20÷2

亮亮的方法：（80+60）×30÷2+（80+60）×30÷2

北极的方法：60×60+30×20÷2+30×20÷2

萱萱的方法：60×60+30×20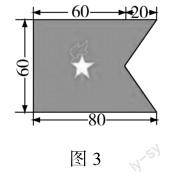

博艺的方法：60×30+30×20÷2+60×30+30×20÷2

通过上述“巩固基础”习题，让学生在不知不觉中内化了“组合图形的面积”计算的重要策略———分割求和、添补求差，同时看到“组合图形”与“基本图形”之间的关联，感悟同类事物的各种特殊情形之中蕴含的“同一性”与“相似性”，明白从特殊到一般的推理过程，实现归纳推理能力的提高与发展.

（二）变式练习———按需选择，融通推理方法

完成“巩固基础”习题后，教师并未停止“探”“思”之步，而是通过“选做题”，巧妙地将“生活”与“数学”结合起来，为学生提供推理训练的平台.这里提到的“选做题”通常是以“巩固基础”习题改编、创编而来，旨在“变”中养成“观察———猜测———验证”的推理习惯.为此，课堂上教师利用多媒体技术展示了“变式练习”的两道题目，即：

变式一：画一画小美、亮亮、北极、萱萱和博艺五名同学的想法，并说一说推理的过程.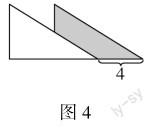

变式二：两个相同的直角三角形（两条直角边分别8，6）重叠在一起（图4），求图中阴影部分的面积？并说一说你的想法.

“变式一”与“变式二”并不做硬性要求，而是让学生结合自身需求进行自主选择.通过“变式一”与“变式二”，即能够拓展学生思维的深度与广度，促使学生养成良好的思维习惯，又能够强化学生对“转化”本质的认识，将复杂转变为简单、将未知转化为已知，实现演绎推理能力的提高与发展.

学习，从本质上来说，就是解决问题的过程，但在“双减”政策下，该过程不能再是传统“兜售式”课堂上的“师来问，生来答”“问的浅，张口答”，这就需要教师据“疑”设“问”，从传统的“被动提问”“照搬教材”“闭门造车”，走向新形势下的“自主提问”“谨慎思考”“探讨交流”.因而以发展推理能力为目标的小学数学说理课堂上，教师理应站在学生的视角与立场，引领学生历经审视、关联、猜想、验证，促使学生“思”“探”“交流”的过程中自主推理、掌握推理方法、发展推理能力，真切地培养小学生的说理能力、发展小学生的推理能力.

【参考文献】

[1]黄丽环.关注小学数学课堂，发展学生推理能力[J].教学管理与教育研究，2020（06）：82-83.

[2]林琳，罗鸣亮.在说理课堂中看见真实学习———“组合图形的面积”教学实践与思考[J].小学数学教育，2022（Z1）：114-116.

[3]赵炜.让“说理”成为数学课堂的主旋律[J].数学教学通讯，2022（01）：35-36.