基于CFD的拖网网板模型参数对水动力试验的影响研究

王一博,初文华,张怀志,曹 宇,崔森琦,武树龙

(1 上海海洋大学海洋科学学院,上海 201306;2 国家远洋渔业工程技术研究中心,上海 201306;3 上海海洋可再生能源工程技术研究中心,上海 201306;4 上海海洋大学工程学院,上海 201306)

网板是单船拖网系统中实现网口扩张、增加扫海面积的重要属具,其水动力性能直接影响网具的捕捞效率[1]。水槽模型试验能够在可控条件下相对准确地获取网板水动力性能系数,是设计和开发网板过程中十分重要的技术手段[2-3]。

刘志强等[2]采用单因素试验法,利用水槽模型试验与数值模拟研究立式双曲面网板在不同展弦比、弯曲度、后退角下的水动力性能。刘景彬等[4]基于计算流体力学(CFD)方法对比分析了3种尺度比 (1∶2、1∶3和1∶4)及3种板面厚度 (2 mm、5 mm和10 mm) 下的模型网板的升/阻力系数及流场分布。朴倉斗等[5]选用板面厚度为2 mm及2.5 mm的不锈钢材料模型开展水槽试验,对比5种不同弯曲度立式曲面网板的水动力性能。山崎慎太郎等[6]选用尺度比为1∶4的模型开展水槽模型试验分析比较矩形V型曲面网板与矩形平面网板的水动力性能。Chu等[7]利用水槽模型试验结合数值模拟研究冲角、展弦比、板面折角等不同结构参数对立式曲面V型网板水动力性能的影响。Xu等[8]通过水槽试验结合数值模拟研究矩形V型网板的水动力性能。Takahashi等[9]对立式双翼开缝网板开展水槽模型试验与数值模拟分析,研究其在不同冲角下的水动力性能。You等[10]采用尺度比为1∶10的双翼型超升降拖网网板模型开展一系列水槽试验,研究其在大冲角下的水动力性能;此后其通过水槽试验结合数值模拟,研究了最大相对弯度为15%、展弦比分别为0.5、1.0、1.5和2.0的曲面网板在翼尖堵塞和不堵塞情况下的水动力性能[11]。

结合学者的前期试验研究结论发现,拖网网板的水动力模型试验结果常因尺度效应等各种因素出现不同程度的试验误差。除人为误差、量具误差等不可避免的误差因素外,尺度比、加工材料等各种试验模型参数的变化,均可能引起试验结果出现不同程度的偏差。

为系统地分析拖网网板水槽模型试验过程中,模型参数对水动力性能测试结果的影响,本研究选取立式V型曲面网板为研究对象,基于水槽模型试验结合CFD方法,探究模型尺度比、板面厚度及加工材料对其水动力性能试验的影响规律,旨在为拖网网板水动力模型试验的设计与开展提供理论参考。

1 材料与方法

1.1 试验研究方法

1.1.1 试验模型

立式V型曲面网板模型制作如图1所示。

本研究选取立式V型曲面网板为研究对象,具体结构形式如图1a所示,其上设置开缝结构,可以达到改善背部流态、减少阻力的作用,从而提高网板的水动力性能[12-14]。

为确保该网板水槽模型试验的有效开展,在综合考虑水槽试验区域流场尺寸及测力设备有效量程的基础上,设计加工长度比尺为14∶1的网板水动力试验缩比模型,如图1b所示,模型网板翼展长为l=380.86 mm,翼弦长为b=133.98 mm,板面折角为d(dihedral angle)=168°,展弦比为λ=2.9。由于该网板的板面形状为曲面,同时还有多条弧形加强筋,为保证模型加工精度及从经济性的角度考虑,本研究在大量前期调研基础上,选用3D打印技术加工该网板的试验缩比模型,模型选用ABS材料。此外,由于本模型长度比尺较大,网板板面厚度在等比缩小后将极其薄弱,考虑到试验过程中模型的结构稳定性与安全性,将模型板面厚度增加至4 mm,而这一模型结构改进措施对水动力试验结果的影响,将在本研究中进行分析。

1.1.2 试验设备

本次网板水动力性能试验于2021年11月在上海海洋大学国家远洋渔业工程技术研究中心动水槽中进行,试验段长15.0 m,宽3.3 m,深2.3 m,最高水深 2.0 m,流速0～1.5 m/s连续可调。配备水槽流速检测仪器与六分力传感器(范围0～500 N,准确度0.1%)。

模型试验设计如图2a所示。网板固定在六分力传感器末端,由长度为0.5 m的金属杆连接,距水槽入口4.2 m。试验水深0.63 m,水温T=23.4 ℃,水密度为 998.23 kg/m3。试验过程如图2b所示。

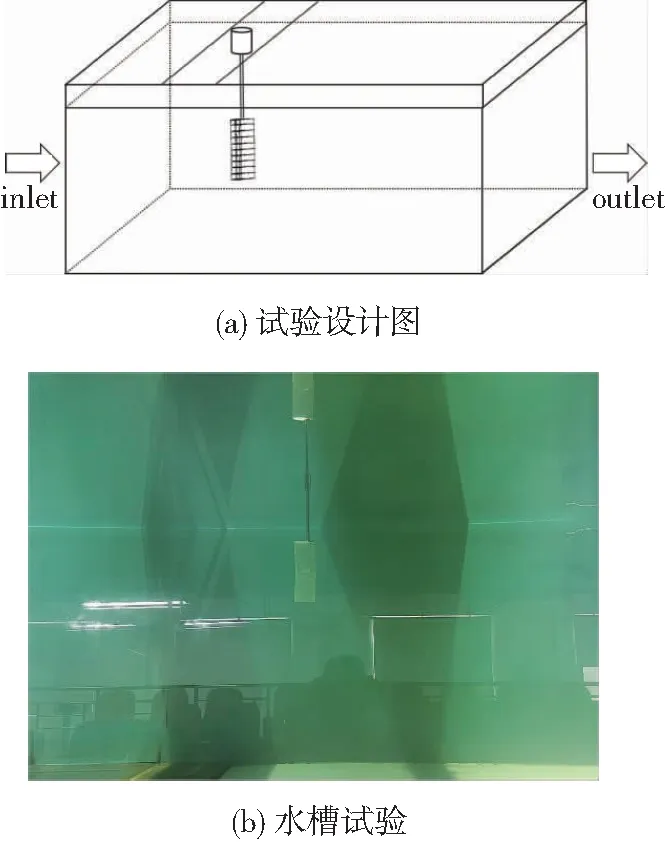
图2 立式V型曲面网板水槽模型试验

定义动水槽水流方向为x轴正向,竖直向上方向为z轴正向。试验过程中将流速依次设置为0.6 m/s、0.7 m/s、0.8 m/s、0.9 m/s、1.0 m/s,分别测得模型网板在不同冲角(α=0°～70°)下X、Y、Z三个方向的受力情况。

1.2 数值研究方法

1.2.1 技术思路

试验模型的加工需要耗费大量时间成本与经济成本,考虑到本研究内容中,涉及大量不同结构参数的试验模型,而每个结构参数的改变都需要生成一个新的试验模型,因此,从研究的经济性角度出发,同时在保证计算结果有效性与满足精度要求的前提下,本研究采用数值模拟与水槽试验相结合的研究方法。在上述试验研究的基础上,首先基于CFD方法建立与水槽模型试验相同尺度和工作条件的数值模型进行计算分析,并将数值计算结果与水槽模型试验结果进行对比,验证数值模型的有效性。在此基础上,模型尺度比、板面厚度等结构参数的改变均通过建立不同的数值计算模型来实现。

1.2.2 网板水动力性能数值计算模型

采用CFD软件 ANSYS Fluent 建立网板水动力性能数值计算模型(图3)。流场区域长X=2 740 mm(7l)、宽Z=1 762 mm(4.5l)、高Y=1 174 mm(3l),网板前缘距水流入口距离为2l[15]。流场采用四面体网格(非结构网格)进行计算。模拟计算使用有限体积法对控制方程进行离散,求解方法为 SIMPLE 算法,湍流模型采用RNG k-ε模型,可在考虑湍流漩涡的同时有效改善不同雷诺数下的计算精度[16-20]。

图3 计算区域设置

模型边界条件设置如图4a所示。上游入口处设定为速度入口边界(velocity inlet),方向沿X轴正向,流速为0.9 m/s,湍流强度设定为5%,湍流强度比设定为3,湍流粘度比为10。下游出口设定为完全发展自由出流边界(pressure outlet),网板结构表面及计算域边界设定为不可滑移壁面(no slip wall)。为提高计算精度,网板边界处网格设置沿网板表面膨胀 3层,增长率为1.2,壁面函数选择适合高雷诺数流动的标准壁面函数,如图4b所示。

图4 流场边界条件设置及网板表面边界处理

1.2.3 网格独立性检验

本研究对同一工况采用不同网格数量的模型进行网格独立性测试,测试结果如表1所示。

表1 网格独立性测试结果

从数据的相对偏差可以看出,计算精度会随网格密度增加逐渐提高。当网格单元数小于700万时,计算结果无法收敛;当网格单元数超过1 100万,流体力学指标趋于稳定,y+值在30左右。基于此,本研究选用模型D开展立式V型曲面网板水动力性能计算,在网格设置中将第一层网格厚度设置为4.2×10-4m(y+≈15),计算区域的单元数和节点数分别为1.13×107和2.07×106,网格尺寸最小值为7.46×10-2mm,最大值为26.785 mm。

1.2.4 网板结构响应数值计算模型

为在数值计算模型中系统地还原水槽模型试验中的工况,从而进一步分析模型参数的变化对网板水动力试验的影响机理,本研究基于流固耦合模型,综合考虑网板在水动力模型试验中的受力情况(水动力、连接杆的约束力),同时计及模型材料建立网板结构响应数值计算模型如图5所示。

由于网板结构较为复杂,将总体网格控制尺寸及关键受力部位网格尺寸均定义为1 mm,网格尺寸缓慢过渡,节点数为813 850,单元数为1 458 387。钢材料密度为7.85×103kg/m3,泊松比为0.3,杨氏模量为2.1×105MPa;ABS材料密度为1.03×103kg/m3,泊松比为0.408 9,杨氏模量为1 628 MPa。网板与连接杆接触处施加固定约束(Fixed Support),限制其自由度。

1.2.5 数值计算工况设置

为系统地研究模型尺度比、板面厚度以及加工材料等不同模型参数对立式V型曲面网板模型试验结果的影响机理,本研究设置了如下几组对比计算工况。

1)改变模型尺度比,分别将原型网板按照尺度比8∶1、11∶1、14∶1、17∶1、20∶1进行缩放,计算分析其在不同冲角(0°、10°、20°、30°、40°、50°、60°、70°)下的水动力性能。

2)改变模型厚度,在相同尺度比(14∶1)下分别将模型网板板面厚度设置为3 mm、4 mm、5 mm、6 mm,计算分析其在不同冲角(0°、10°、20°、30°、40°、50°、60°、70°)下的水动力性能。

3)改变模型材料,对同一缩比模型(尺度比14∶1,板面厚度4 mm)分别采用金属材料(钢)与3D打印材料(ABS)进行数值建模,计算分析其在模型试验工况下的结构响应。

1.2.6 数据处理

立式V型曲面网板水动力性能系数主要为升力系数Cl,阻力系数Cd,升阻比K;主要结构参数为展弦比λ;主要试验参数为冲角α,雷诺数Re,具体定义如下:

(1)

(2)

(3)

(4)

(5)

式中:l为翼展(m);S为网板法向上的投影面积(m2);v为来流速度(m/s);ρ为流体密度(kg/m3);b为网板弦长(m);μ为流体动力粘度(kg/m·s);Fd为网板阻力(N);Fl为网板升力(N);Cl为升力系数;Cd为阻力系数。其中,升力系数和阻力系数均为进入自动模型区后测量值的平均值。

对于网板的结构响应采用静态结构分析方法,计算网板的变形、等效弹性应变和等效应力。式(6)为等效应力与主应力的关系;式(7)为等效应变εe的计算公式。其中v′为有效泊松比。

(6)

(7)

2 结果与分析

2.1 数值模型有效性验证

为验证所建立数值计算模型的有效性,本研究首先基于CFD方法建立与水槽模型试验相同尺度与工作条件的数值模型进行计算分析,并将数值计算结果与水槽模型试验结果进行对比,对比结果如图6所示。

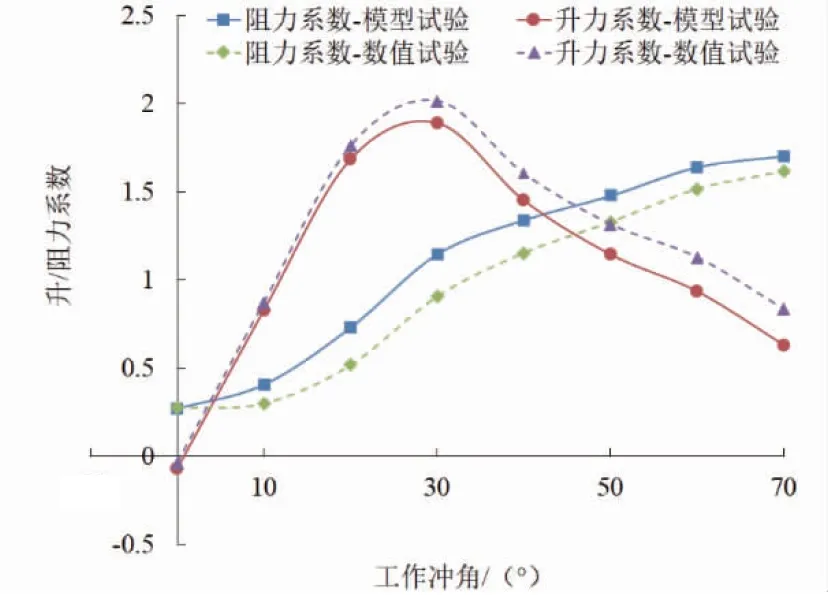
图6 数值模型计算结果与水槽模型试验结果对比

由图6可知,数值模型计算得到的立式V型曲面网板的升/阻力系数随冲角的变化趋势与水槽模型试验一致,冲角在 0°～ 30°范围内,升力系数随着冲角增加而增大,最大升力系数对应冲角为 30°;当冲角大于30°时,随冲角的继续增加升力系数逐渐减小;阻力系数则始终随冲角的增加而增大。从升/阻力系数值来看,在小冲角(小于20°)时,数值模型计算结果与水槽模型试验结果相对误差很小,而随冲角的进一步增加,二者的相对误差略有增大,这一现象的产生原因将在本研究后续进行分析。升力系数的误差范围在3.3%～20.3%,阻力系数误差范围在0.7%～23.9%,在误差允许范围内,数值计算结果有效性较高。

此外,基于不同流速下的试验数据计算得到网板升/阻力系数与雷诺数及冲角的关系如图7所示。

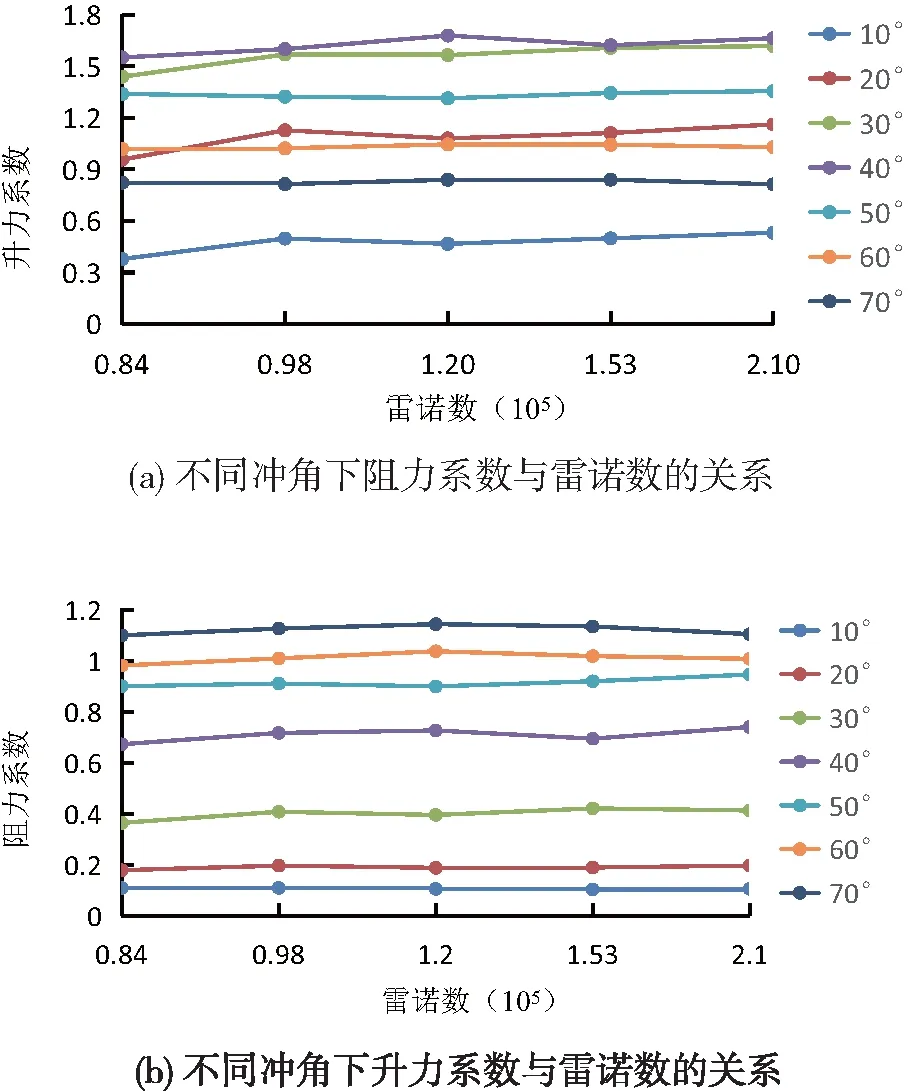
图7 立式V型曲面网板不同冲角下的水动力系数阻力系数与雷诺数的关系

可以看出,升力系数与阻力系数在各冲角下随雷诺数变化均无显著改变,由此可知本研究中设置的各项试验工况(流速、模型尺度)均在自动模型区范围内。

2.2 模型尺度比对网板水动力模型试验的影响

水槽试验设计过程中,缩比模型的尺度比选择是首要及关键步骤,需要根据试验水槽尺寸、测量装置量程、模型制作等多方面因素综合考虑与设计。模型尺度太小会导致试验精度无法保证,而尺度太大时,网板周围流场流态会容易受到水槽流场边界效应的影响而发生改变,进而影响水动力试验结果,此外,大尺度模型的加工成本也是试验设计时需要考虑的问题。

为深入研究模型尺度比对网板水动力模型试验的影响规律,图8给出了不同尺度比(8∶1、11∶1、14∶1、17∶1、20∶1)的立式V型曲面网板模型在相同流速(0.9 m/s)下的升/阻力系数对比及偏差。

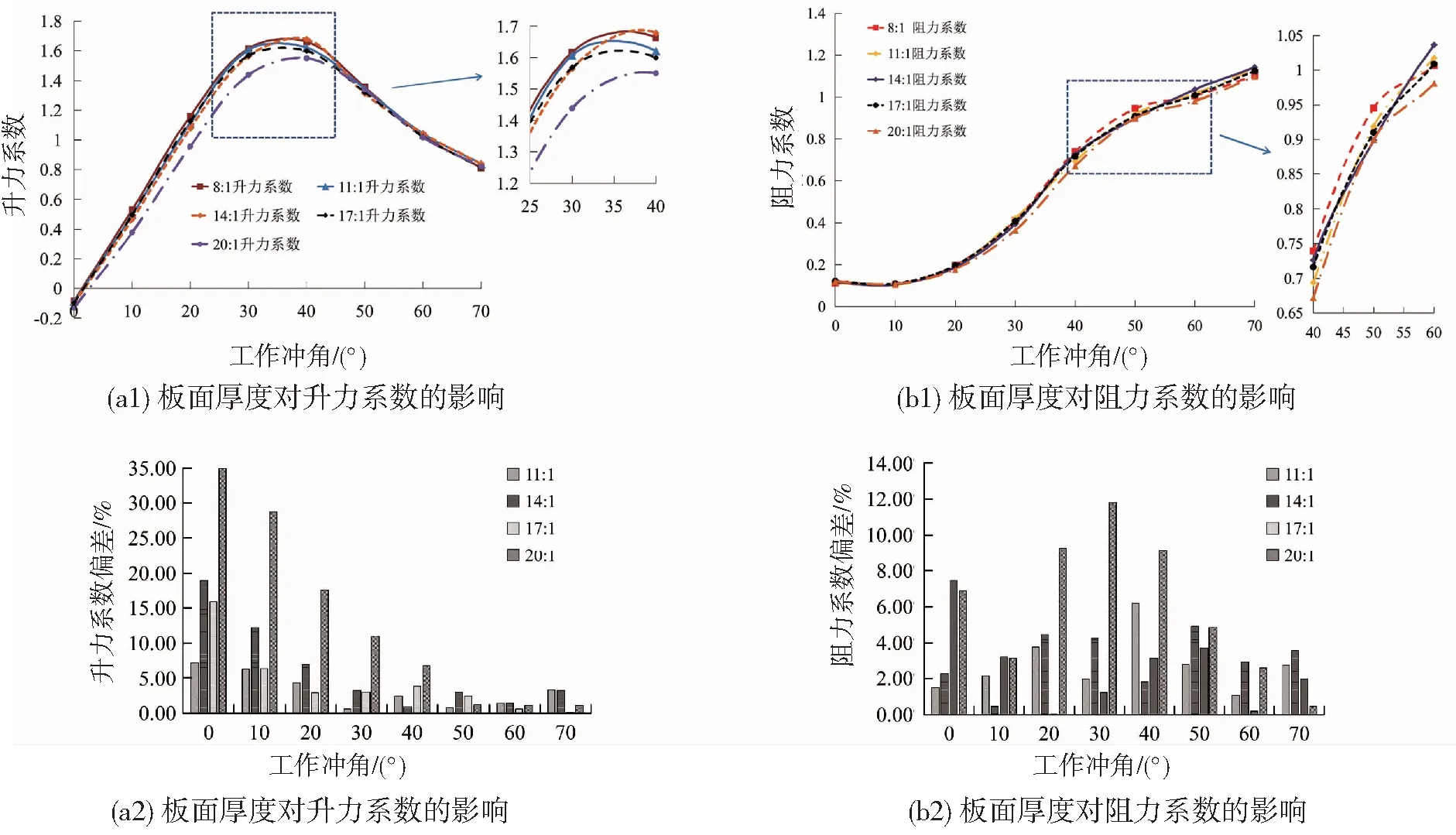
图8 模型尺度比对立式曲面V型网板水动力性能的影响

从图8a1、8a2中可以观察到,模型尺度比对升力系数变化趋势的影响并不显著,仅小尺度模型的最大升力系数对应冲角比大尺度模型略有增加;相较而言,模型尺度比对升力系数值影响更为显著,特别是在小冲角(α<30°)时,当模型尺度比增至20∶1,由于模型尺度缩小过多,计算结果与其他尺度比模型出现明显偏差,而当模型尺度比小于17∶1时,不同尺度比模型计算得到的升力系数值偏差不大(15%以下)。从图8b1、b2中可以观察到,相较于升力系数,模型尺度比对阻力系数的影响更不显著(偏差均小于12%),不同尺度比的模型阻力系数曲线与系数值均未有明显偏差,仅在冲角为30°左右时,最小尺度模型(尺度比20∶1)阻力系数差异较为显著(偏差12%左右)。因此,在设计该网板水动力模型试验时,除考虑到模型加工成本外,应尽可能减小模型尺度对试验结果精度的影响,将其控制在17∶1以下。由于不同结构型式的网板,水动力性能随结构的变化规律不同,因此本研究计算得到的尺度比范围仅为参考值,具体尺度比尚需根据不同网板的结构型式进行具体计算。

为进一步探究模型尺度比的改变对网板水动力性能的影响机理,分析不同尺度比模型水动力性能产生差异的具体原因,图9给出了不同尺度比的网板模型在40°冲角时的网板中部截面附近流场分布情况。从图9中可以观察到,尺度比的改变对于网板附近流场分布的影响不显著,不同尺度比的网板模型迎流面高压区与背流面低压区形状相似、压力值范围接近,导致各尺度比模型升、阻力系数变化趋势亦无明显区别。当模型尺度较小时,网板背流面涡的尺度显著减小,同时网板迎流面高压区面积与背流面低压区面积均较大尺度模型有所降低,导致网板升力系数相较大尺度模型而言显著降低(如图9所示)。

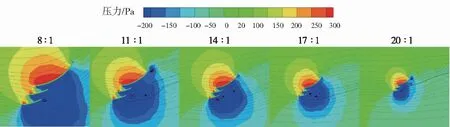
图9 不同尺度比的网板模型中部截面附近流场分布(α=40°)

2.3 模型板面厚度对网板水动力模型试验的影响

由于网板模型长度比尺较大,实际网板板面厚度较小,因此在等比缩小后模型板面将变得极其薄弱,考虑到试验过程中模型的结构稳定性与安全性,需将模型板面厚度适当增加。为研究这一模型结构的改进措施对水动力性能产生的影响,图10给出了不同板面厚度2 mm(不加厚)、3 mm、4 mm、5 mm、6 mm的网板模型升、阻力系数对比情况。由图10可知,网板模型板面厚度的改变对升、阻力系数的变化规律影响显著,对升力系数的影响主要反映在大冲角(α>30°)时,而对阻力系数的影响则主要反映在小冲角(α<30°)时。

板面加厚时最大升力系数对应冲角略有减小,同时升力系数值在大冲角下随板面厚度的增加呈现降低趋势;当板面厚度增加较小(≤4 mm)时,对网板模型升力系数影响不显著(偏差15%以下)。在设计网板水槽试验缩比模型时,需综合考虑模型结构的稳定性及厚度增加对水动力性能系数的影响,适当增加网板模型板面厚度(板面增厚不超过2倍),这一厚度增加范围同样需根据不同网板的结构型式进行具体计算。

为进一步探究网板模型板面厚度的改变对其水动力性能的影响机理,分析不同板面厚度的模型水动力性能产生差异的具体原因,图11给出了不同板面厚度的网板模型在30°冲角时的网板中部截面附近流场分布情况。

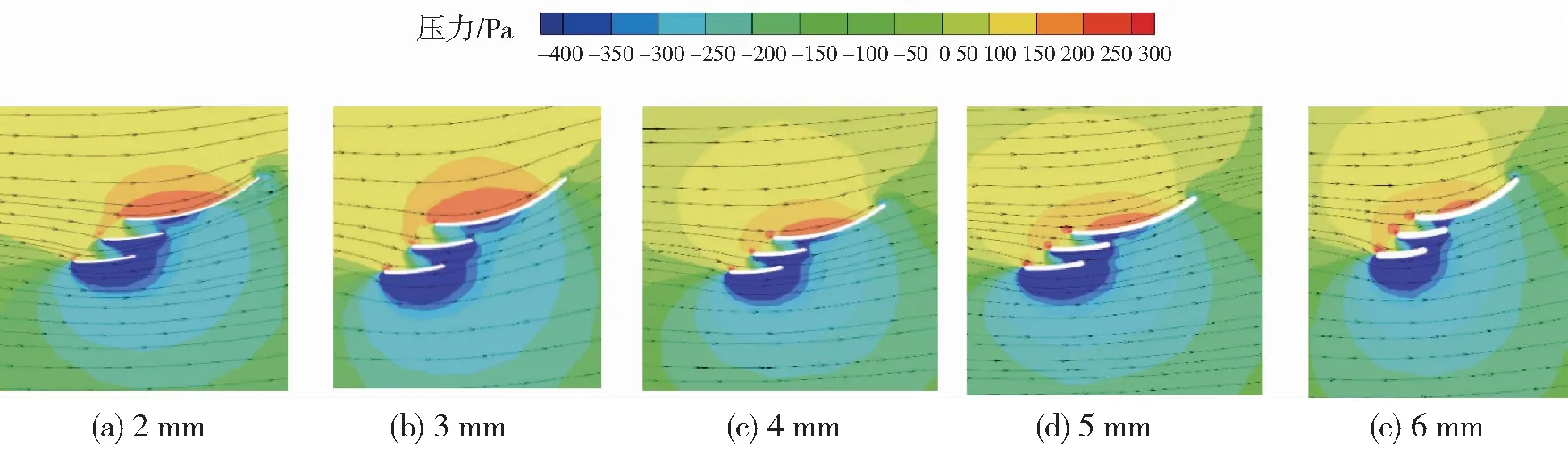
图11 不同板面厚度网板模型中部截面附近流场分布(α=30°)

从图11中可以观察到,板面厚度的变化并未引起网板模型迎流面高压区与背流面低压区形状的改变,但随着模型板面厚度的增加,网板迎流面高压区面积显著减小,而低压区面积变化不明显,从而导致了网板升力系数随板面厚度的增加呈现降低趋势;板面厚度小于4 mm时,网板迎流面高压区面积与板面不加厚(2 mm)时基本一致,此时升力系数没有显著变化,而当板面厚度显著增加(大于5 mm),网板迎流面高压区面积的大幅度减小导致了升力系数的显著降低,这一规律与图10a1、图10a2完全一致。

2.4 模型材料对网板水动力模型试验的影响分析

从图6的数值计算结果与水槽模型试验结果的对比中发现,二者的偏差并非在各个冲角下保持一致,而是会随冲角的增加逐渐增大。通过水槽试验模型与数值计算模型的对比发现,由于水槽试验中采用的缩比模型选用ABS材料进行加工,该种材料刚性相对较弱,因此在试验过程中模型可能会随水动力的增加产生一定的局部位移与变形,而数值计算模型中将网板材质设置为刚性[21-22],即控制模型在水中不产生位移与变形。由此推测这一模型局部位移与变形是产生数值计算结果与模型试验结果偏差的主要原因。为验证这一推断,图12给出了基于流固耦合模型计算得到的两种不同材质(结构钢与ABS)的网板模型在水动力试验过程中相同工况下的变形情况,同时为便于比较分析,还给出了进行板面加厚(4 mm)之后的ABS材料网板模型的变形情况。

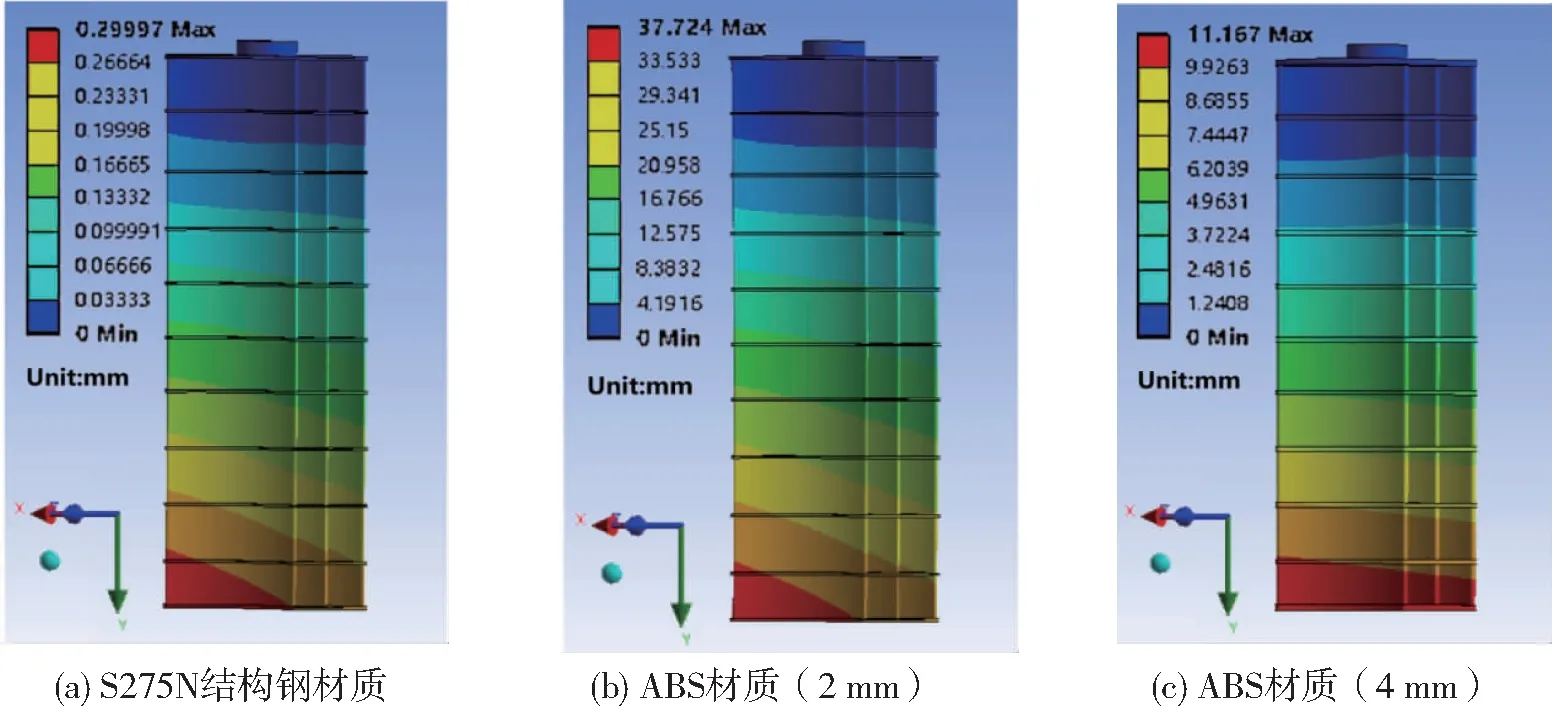
图12 不同材质网板模型变形情况

从图12中可以明显地观察到,由于试验过程中网板上端通过连接杆固定,下端自由,网板底端会产生一定的变形;在相同的试验工况下,ABS材料的网板模型变形较结构钢材质的网板明显较大,进而导致二者水动力系数的显著差异。此外,当ABS材料的网板模型板面厚度增加,会在一定程度上提高模型的刚性,因此在相同工况下,其结构变形较未加厚的ABS材料网板模型显著减小,由此可以推断,在开展网板水槽模型试验时,板面厚度的适当增加,可以在一定程度上减小由于模型底部变形引起的试验误差。

图13进一步给出了不同材质的网板模型最大变形随冲角的变化情况,

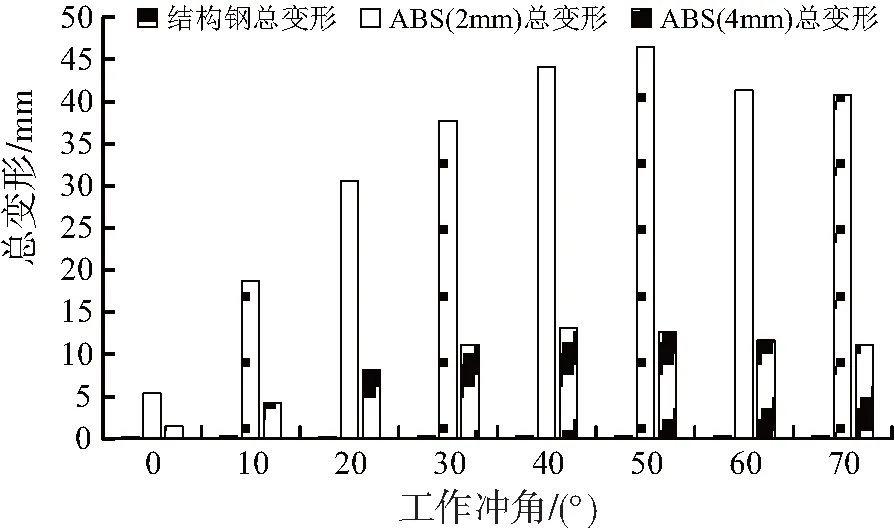
图13 不同材质网板模型最大变形随冲角变化情况

从图13中可以清楚地观察到,相同板面厚度的ABS材料模型在各冲角下的变形均显著大于结构钢材质的网板模型,同时,随冲角的增加,二者的差距显著增大,由于网板底端的变形是在水动力作用下产生,由此就解释了数值计算结果与水槽模型试验结果的偏差随冲角的增加逐渐增大这一现象。同时也可以进一步看出,板面厚度增加后,ABS材质的网板模型在各冲角下的变形均显著减小,虽然较结构钢材质的网板仍有偏差,但可在一定程度上降低结构变形引起的试验误差。结合2.3节中板面厚度对模型试验结果的影响分析可知,板面厚度在试验过程中不能大幅度增加,否则会从另一个方面影响试验结果的精度,因此在设计网板模型的板面厚度时,需要结合材料的刚性及对水动力性能的影响两方面进行综合考虑。

3 讨论

3.1 模型试验与数值模拟结果偏差

将网板数值模型计算结果与水槽模型试验结果进行对比,结果表明升、阻力系数变化趋势吻合较好,最大升力系数出现在30°左右,阻力系数呈上升趋势(图6),这与Chu等[7]研究结果一致。升力系数的偏差范围在3.3%～20.3%,阻力系数偏差范围在0.7%～23.9%。分析偏差产生原因主要有如下3点:一是数值模拟中模型网板表面光滑,因此计算过程中不会产生摩擦阻力,由此导致数值计算阻力偏小;二是在数值模型中流场内只有网板,而没有水槽试验中用于连接模型网板与六分力传感器的连接杆,而在试验过程中测得的阻力为连接杆与网板所受阻力的合力,这是导致阻力计算值较试验结果偏小的另一原因;三是水槽模型试验过程中由于试验环境限制极其易产生水流不稳定与模型结构振动,进而导致试验结果存在误差。

此外,数值模型建立过程中,网格精度控制与参数设置均会对计算结果产生重要影响。分析数值模拟计算结果偏差的主要原因有:一是模型简化与初始条件设置与实际试验工况不完全相同的建模误差;二是数值算法本身对数学模型与定义域的离散误差;三是包括舍入误差和迭代误差的计算误差[23-29]。其中建模误差为主要误差原因,在尺度效应、板面厚度和模型材料等结构参数对模拟结果的影响中均有体现,前文所讨论的忽略网板摩擦阻力与连接杆阻力的误差也属于建模误差。离散误差与计算误差对结果偏差的影响程度有限,主要受到网格类型、网格尺度以及边界条件等的影响。Xu 等[8]对比了4种不同网格密度下网板升/阻力的差异,结果显示网格数量从9.3×105增至2.3×106,计算精度略有提高。左玲玉等[23]对比分析了3种结构网格与3种非结构网格在不同冲角下升/阻力系数差异,结果显示结构网格模型的离散误差小,且细网格模型具有更好的网格收敛性。由此分析,本研究中采用四面体非结构网格可能也是导致误差较为明显的原因之一。

有学者[30-33]研究表明,CFD数值模拟中,在考虑湍流模型封闭系数认知不确定性和来流条件随机不确定性的情况下,通过融合混合不确定性量化、全局灵敏度分析,并根据似然样本策略对关键系数加以修正,可以有效修正CFD模型,减小模拟误差。但目前仍未有学者研究CFD模型修正方法在网板数值模拟中的应用。今后可引入该类方法来实现减小网板数值模拟结果的误差,以便更准确地计算网板水动力性能。

3.2 网板周围流场可视化

探究网板周围流场流态对于分析网板模型试验中水动力性能变化规律至关重要,也是解释模型参数对网板水动力模型试验影响机理的有力依据。目前实现网板周围流场可视化的方法主要有3种:线条法、气泡法和CFD数值模拟法[2]。相比于线条法与气泡法耗时长且只能定性观测分析网板周围流态变化的缺陷,CFD数值模拟技术具有高效、低成本、精确性好等优点[3]。刘景彬等[4]、Xu等[8]先后采用CFD数值模拟对网板周围流场进行了可视化分析。

本研究基于CFD方法分别对不同尺度比与不同板面厚度的立式V型曲面网板流场进行了可视化处理,发现涡的尺度、网板迎流面高压区面积与背流面低压区面的变化均会对网板水动力性能产生显著影响:随着模型尺度比的减小,网板背流面涡的尺度、迎流面高压区面积与背流面低压区面积均有所降低,进而导致小尺度比网板的升力系数小于大尺度网板。这种趋势与刘景彬等[4]发现的升/阻力系数随分离涡的增大而增大的结果基本一致。

4 结论

本研究以南极磷虾拖网作业时常用的立式V型曲面网板为研究对象,采用水槽模型试验与数值模型计算相结合的方法,探究模型尺度比、板面厚度及模型材料对其水动力性能试验的影响规律,得出的主要结论如下:

(1)模型尺度比的改变对网板升力系数与阻力系数曲线形状改变均不显著,其主要对网板升力系数值产生较大影响,当模型尺度缩小过多(20∶1),升力系数在小冲角(α<30°)时偏差明显。设计网板水动力模型试验时,在综合考虑水槽试验区域流场尺寸、测力设备有效量程及模型加工成本的基础上,应使得模型尺度尽可能大,减小模型尺度对试验结果精度的影响。

(2)模型板面厚度的改变对网板升、阻力系数均会产生显著影响,对升力系数的影响主要反映在大冲角(α>30°)时,而对阻力系数的影响则主要反映在小冲角(α<30°)时。试验设计时,为提高模型结构稳定性可适当增加板面厚度,但增厚范围需不超过2倍(不同结构型式网板试验模型板面增厚范围可参考此范围具体计算后确定),因为大幅度的厚度增加将会引起升力系数值在大冲角下的显著降低。

(3)非金属材料由于刚性不足会在水槽模型试验过程中容易因受力后产生一定的位移与变形而引起试验结果的偏差。可采取增加模型板面厚度的方式减小此偏差,但具体增厚范围需结合结构的刚性及对水动力性能的影响综合考虑。