柔性网具和浮体与打捞船间的耦合影响

高 瑞,王一帆,张倍铭,吴贺贺,林 东,叶建设

(1 中国水产科学研究院渔业机械仪器研究所,上海 200092;2 青岛海洋科技中心,青岛 266237;3 北京跟踪与通信技术研究所,北京 100094;4 海鹏海洋工程(上海)有限公司,上海 201803)

高海况打捞技术是中国海洋捕捞技术的拓展与延伸[1]。高海况打捞系统主要由打捞船、被打捞浮体及打捞网具组成。被打捞浮体与打捞船在高海况下易受风浪影响,且相对于船舶,浮体尺寸很小,其运动还易受到船舶辐射扰流干扰;打捞网具是由目脚、结节、沉子、浮子等构件所组成的复杂柔性结构体,各构件因其型式、材质等不同,所受波浪力、惯性力、拖曳力等各不相同。因此,打捞船、网具与浮体在高海况下受到的流体作用力具有强非线性特点,三者之间的任一运动状态的改变,都会影响到整个系统的运动响应。

单独针对船舶或浮体的运动响应研究方面,许勇等[2]采用三维势流理论及多体动力学理论建立了波浪中近距离并行航行多船波浪作用力及运动响应的计算模型,并通过模型试验进行了验证。Zhou等[3]基于SST k-Ω湍流模型,比较分析了单船与两船并行航行的水动力差异。郑平宇等[4]利用AQWA软件开展了补给船与接收船并行补给过程中的耐波性研究,获取的结果与谱分析结果进行了比较。谢楠等[5]利用三维线性势流理论计算了两个浮体的水动力相互作用,并与试验结果进行了对比。杜一豪等[6]采用统计学方法深入探讨了不规则波浪作用下Wigley型船的运动响应问题,结果表明船舶横摇方向与升沉和纵摇方向随机运动的响应特征有显著差异。陈京普等[7-8]研究了10万吨级油轮在长峰和短峰不规则波中的运动响应问题。张杰等[9]对国际集装箱标模在迎浪规则波中的运动响应和波浪增阻等进行数值计算,计算得到的船体运动幅值能与试验结果相一致。吕向琪等[10]采用频域Rankine面元法计算了Wigley I、Wigley III和S175在有航速时船舶的水动力系数、波浪激励力和运动响应。李冬琴等[11]采用单参数Lagrangian支持向量回归算法用于训练并构建了代理模型以预报船舶耐波性能。

单独针对柔性网具的研究方面,Lee等[12]建立了水下柔性结构数值模型,系统地考虑了材料的刚度和数值稳定性,并且提出了网目合并处理办法。孙霄峰等[13]建立了单船拖网网具的集中质量模型,在建立操纵性方程时将船体力、推进器、舵力、风载荷等因素考虑其中。Tsukrov[14]采用等效网单元对网衣系统进行等效合并从而建立了网衣系统的连续有限单元法。Fredheim[15]采用了有限元办法对流力作用下的锥形网衣变形特性,结合模型试验结果研究了目脚和结节水动力系数的取值范围。Wan等[16]考虑了目脚的弹性变形和水动力的耦合作用,获取了水下网具系统的平衡状态和张力分布。林礼群等[17]开展了静水条件下网具与浮体的打捞试验,研究了船舶速度、网口高度、打捞物体吃水深度等参数对网具的影响。陈昌平等[18]基于大涡模拟开展了金属网衣多孔小直径网状结构的水动力响应特性仿真分析,得到了不同目脚尺寸和网线直径组合条件下锌铝合金网衣的平面受力计算结果。陈天华等[19]基于集中质量点法和网目群化技术研究了桩柱式围网单元网片在水流作用下的水动力特性。倪震宇等[20]使用数值计算方法对单锚张纲张网渔具的水动力特性和形状进行模拟,获取了网衣和纲索的张力载荷分布及随流速的变化情况。

针对高海况下的柔性网具与浮体及打捞船耦合影响的研究较为有限,孙洪波等[21]、王飞等[22]、苑志江等[23]、朱克强等[24]、朱军等[25]对船-拖缆或船/缆/体系统开展了操纵性运动仿真分析,但是拖缆为单个缆绳而非网具。

本研究通过数值仿真技术,开展了浮体与打捞船的耦合水动力研究,将浮体运动响应及浮体与船舶相对位置作为设计输入,并开展了浮体与柔性网具的耦合水动力特性研究。

1 数值方法及研究思路

1.1 刚性浮体与打捞船

1.1.1 控制方程

连续性方程与动量方程如下所示:

(1)

(2)

湍流模式采用Realizablek-ε两方程模型,具体表达如下:

(3)

式中:μt为流体涡粘系数,Gk为速度梯度产生的湍动能,Gb为浮力产生的湍动能,Ym为可压缩湍流中波动膨胀的贡献,αk与αε分别为湍动能k与湍流耗散率ε的普朗特数,C2、C1ε和C3ε为常量,Sk与Sε为用户定义的源项。C1为时均应变率的函数,表示为:

(4)

自由液面捕捉采用VOF法,其输运方程如下:

(5)

1.1.2 运动方程

将打捞船与浮体的运动视作刚体运动,本研究主要考虑纵倾与升沉两个自由度,运动方程如下:

(6)

(7)

1.2 柔性网具

网具主要由细长网线、浮子、沉子等构成,可将网具离散为通过无质量杆件连接的质量点的集合。浮子、沉子等视作球体,质量集中于各自形心且其受力作用于质量点上,网线受力及属性(质量、浮力、曳力等)被平均分配给该线段的两个端点结节处,线自身被视为无质量杆件,只传递拉力。网具运动方程如下所示[27,29-30]:

(8)

式中:mi为第i个质量点的质量;Δmi为第i个质量点的附加质量;(ti,bi,ni)为第i个质量点的空间位置坐标;T为质量点受到的拉力,下标x表示受到的x方向上的力,其余类推;F为质量点受到的水动力;W为质量点水中重量,即重力与浮力的合力。

质量点j对质量点i所受拉力由下式表达:

(9)

式中:E为材料弹性模量;d为网线直径;lij为质量点i、j之间的网线实际长度;l0为质量点i、j之间的网线未伸长长度。作用在质量点i上的拉力在空间上的分量由下式表达:

(10)

式中:N表示与质量点i相连的所有质量点的集合。

由于网线、浮子、沉子等网具构件直径相对于波长、波高为小量,且由于其特征尺寸与入射波波长之比小于0.2,可采用莫里森方程计算网具在波浪载荷作用下的水动力,公式如下:

(11)

式中:Cd为阻力系数;A为投影面积;vcx、vcy及vcz为流速在3个坐标轴上的分量。

1.3 重叠网格

针对船体及浮体,采用重叠网格技术实现其运动姿态的模拟。运用重叠网格技术时,一般将计算域分为背景区域和重叠区域,重叠区域即为运动物体的周边区域。各区域网格单独生成,流场数据通过重叠网格边界条件实现耦合。重叠网格示意图如图1所示,船体周边立方体即为重叠区域。

图1 重叠网格示意

2 刚性体模型及计算域

2.1 船与浮体

计算模型缩尺比为1∶10,计算用某打捞船如图2所示,由于计算不涉及船体上层建筑,因而为简化模型信息、减少计算时间,这里不考虑针对上层建筑进行建模工作。

图2 打捞船三维模型

该打捞船主尺度无量纲化后如表1所示。

表1 打捞船主尺度无量纲值

计算用浮体如图3所示,主尺度参数如表2所示。

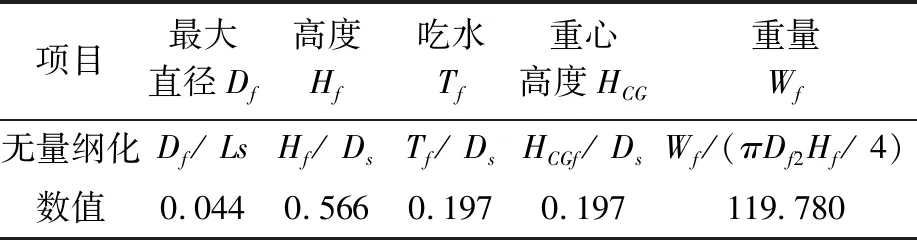
表2 浮体主尺度无量纲值

图3 浮体三维模型

2.2 计算设置

2.2.1 计算域与边界条件

计算域的选取应确保流体在边界处不发生回流以干扰到浮体及打捞船周围区域,同时需综合考虑边界选取对流动特性和计算成本的影响,本研究计算域及边界条件设置如表3所示。

表3 计算域及边界条件设置

2.2.2 网格划分

网格划分具体见图4。

图4 网格划分

维系波浪在整个计算域中不随空间和时间发生数值耗散是波浪条件下数值模拟的重要前提。一般而言,在一个完整波浪的波高方向上,应不少于20个网格数量;在一个完整波浪的波长方向上,应不少于40个网格数量。为将波浪完全包裹,在波浪区域划分网格时,还需将加密网格区域的高度设置为1.2倍的波高。为尽可能减少计算所需时间成本,加速收敛,同时避免波浪在出口处产生回流以影响到船舶及浮体周围流场,在距离船舶2倍波长的下游处,通过设置粗网格对波浪进行数值消波,粗网格在波浪范围的设置基本为波浪区域网格设置的一半左右。

2.2.3 求解设置

设置时间及空间差分均为二阶格式,求解方式采用基于压力的瞬态求解,时间步长为0.005 s,设置时间步长时应保证库朗数小于0.5。库朗数计算公式为:

Co=vC·Δt/min(Δx)

(12)

式中:Co为库朗数;vC为流速;Δt为时间步长;min(Δx)为最小网格尺寸。

2.2.4 计算工况

为获取浮体与船舶之间的最佳相对位置,以便于打捞船对浮体进行打捞作业,根据实际打捞经验给出9种计算工况,见表4。

表4 计算工况

2.3 造波验证

造波算例验证如图5所示。

图5 造波算例验证

根据上述网格及设置策略,以波高0.1 m、波长1.5 m,以规则波均匀流场作为初始值开展造波算例验证,图5a显示了计算20 s后的波形图,图5b显示了波高监测情况。其中,左侧为进口,右侧为出口,出口处往前至2倍波长处设置为消波区。由图5可知,消波区域有效降低了波幅,减少了波的传输能量,防止波在计算域中的回流,造波区域波幅没有明显的衰减。

3 柔性网具模型

3.1 网具等效简化

为反映网具变形及受力情况,建模过程中,仅考虑网线的轴向弹性力,其他诸如质量、浮力等参数都平均分配至网线两端的节点处,波浪载荷同样也加载至节点处。此外,考虑到网具精确建模的计算成本过高,参考国内外相关研究[26-28]对其进行等效简化。

具体而言,以r为等效比,可得到如下关系式:

(13)

deq·Leqtotal=d·Ltotal

(14)

式中:m为横向网目数量;n为纵向网目数量;l为目脚长度;d为目脚直径;Ltotal为网线总长度,下标eq为等效后对应数据。为保持等效后网片的质量相同,目脚等效横截面积由下式计算:

(15)

计算用模型如图6所示。

图6 网具示意图

3.2 网具主要参数

经简化后的网具各构件参数见表5。其中,浮子总浮力2.5 kN,平均分配至图6b中的浮子上,沉子总质量100 kg,平均分配至图6b中的沉子上。

表5 简化后网具各构件参数

3.3 求解设置

为确保计算模型在动态时域分析中能够实现收敛,对网囊和浮体相对位置进行了限定,以确保重物有合理的边界条件约束。分析时,时间步长取0.005 s。

4 结果分析

4.1 打捞船与浮体

以工况3为例,打捞船与浮体在高海况下的升沉、纵摇时历曲线如图7所示。打捞船在高海况下的运动响应呈现较强的周期性变化,且响应幅值也较小。相比打捞船,浮体由于主尺度远小于船舶,且处于长波浪中,波浪力载荷对浮体的影响远大于船舶,体现为波浪中浮体的运动幅值大于船舶运动幅值。

图7 打捞船与浮体运动时历曲线

此外,由于打捞船在开展捕捞作业时与浮体距离较近,浮体除受到波浪载荷外,还受到船体的辐射扰流影响,导致浮体的纵摇响应出现较强的不规则性,图8中打捞船与浮体在波浪中的运动姿态变化体现了这点。

图8 打捞船与浮体运动姿态变化

为分析浮体与打捞船沿船宽及船长方向不同位置受力情况,图9给出不同计算工况下浮体横向受力情况,其中计算工况1～5是浮体在相对打捞船同一纵向位置、不同横向位置下受到的横向力,计算工况6～9是浮体在相对打捞船同一横向位置、不同纵向位置下受到的横向力。

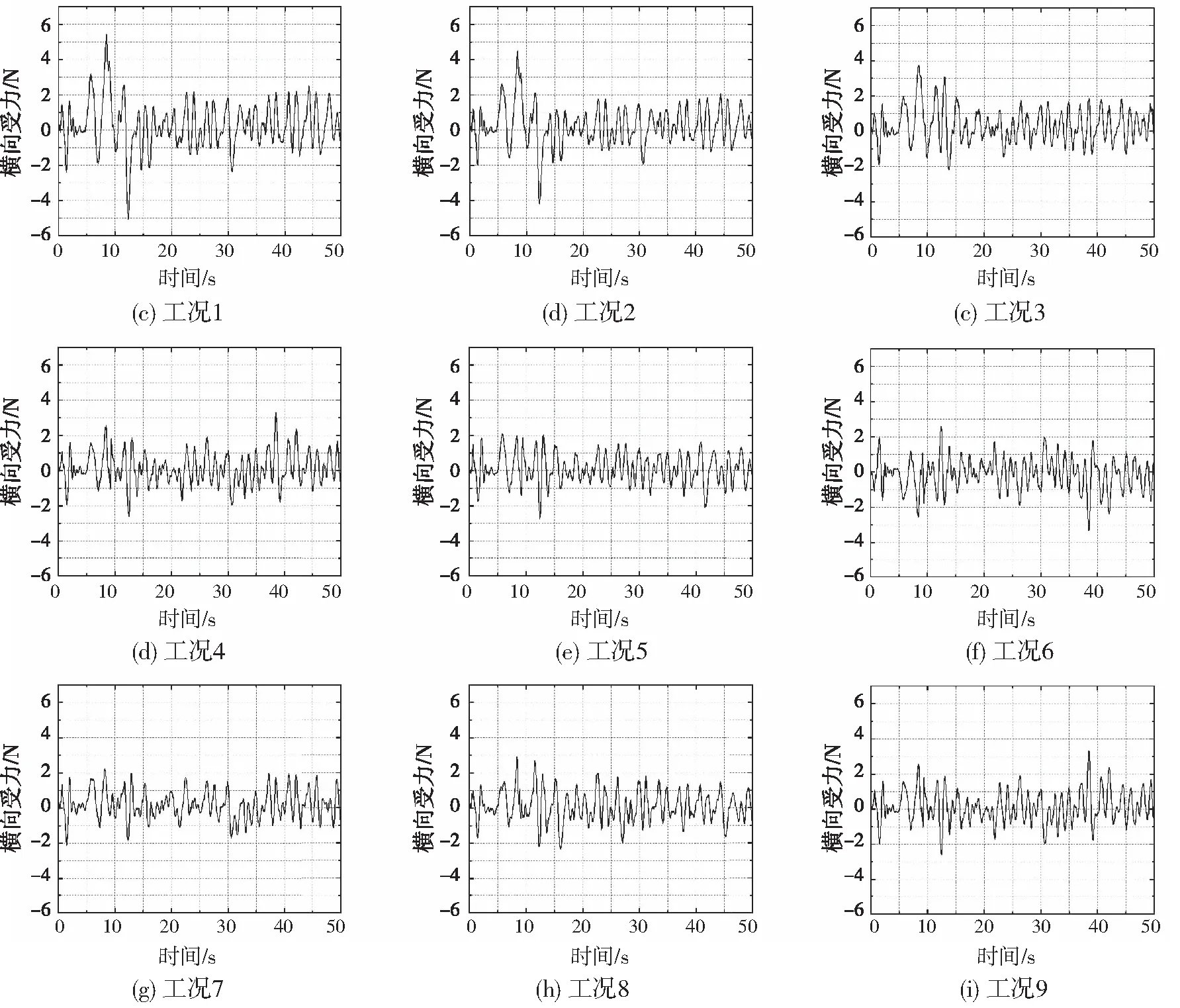
图9 浮体在打捞船不同位置下的横向受力

针对不同横向位置处,浮体受到的横向力不存在明显的相位差。且其大小与浮体及打捞船之间的间距呈现负相关,即当浮体与打捞船间距越近,浮体受到的波浪力及辐射力也越大,其运动情况也更为剧烈。从操作便利性角度出发,当浮体与打捞船间距相对接近时,打捞操作相对便利。因此,从保持浮体在高海况下的稳定性与打捞船在高海况下的操作便利性这两方面考虑,存在一个较为平衡的横向位置。

针对不同纵向位置处,不同工况间存在一定的相位差,尤其以工况6最为明显,这应该与波浪传播方向和船舶纵向船长方向一致有关,浮体在不同的纵向位置,其受到波浪力也存在着一定的相位差。除此外,不同工况下的横向受力大小没有特别明显的变化,说明浮体受到的横向力受浮体与船舶的横向间距影响较大,受浮体与船舶的纵向间距影响较小。总体看,工况3处对应的浮体与打捞船相对位置较优,后续在进行网具与浮体分析时,将以工况3位置及浮体对应运动响应作为设计输入。

4.2 网具与浮体

图10显示了网囊中不含浮体与含浮体时网具在波浪中变形响应情况。当网囊中不包含浮体时,从其运动姿态中可以看出,网具主要随波面运动,并被提上纲绳、沉子与浮子共同限制;当网囊中包含浮体时,浮体大部分浮出水面且随波面运动明显,牵引网囊与其同步运动。另外,网具同时也被提上纲绳、沉子与浮子共同限制。

图10 网具入水姿态

图11给出网具中网囊网线、网身力纲、侧网曳纲以及提上纲绳等构件的受力极值时历曲线,需指出的是,由于模型进行了简化处理,实际每个构件均由若干网线组成,这里仅给出出现极值的网线时历情形。由图11可知,网囊网身整体受力较为平均,侧网上、下曳纲受力差别较大,且侧网下曳纲为网具各部分中受力最大的构件,这是由于侧网上曳纲在浮子的作用下漂浮于水面,而下曳纲在沉子的作用下浸没入水,波浪载荷及浮体运动作用于下曳纲使其张紧程度高于上曳纲。图12为网具总受力曲线。

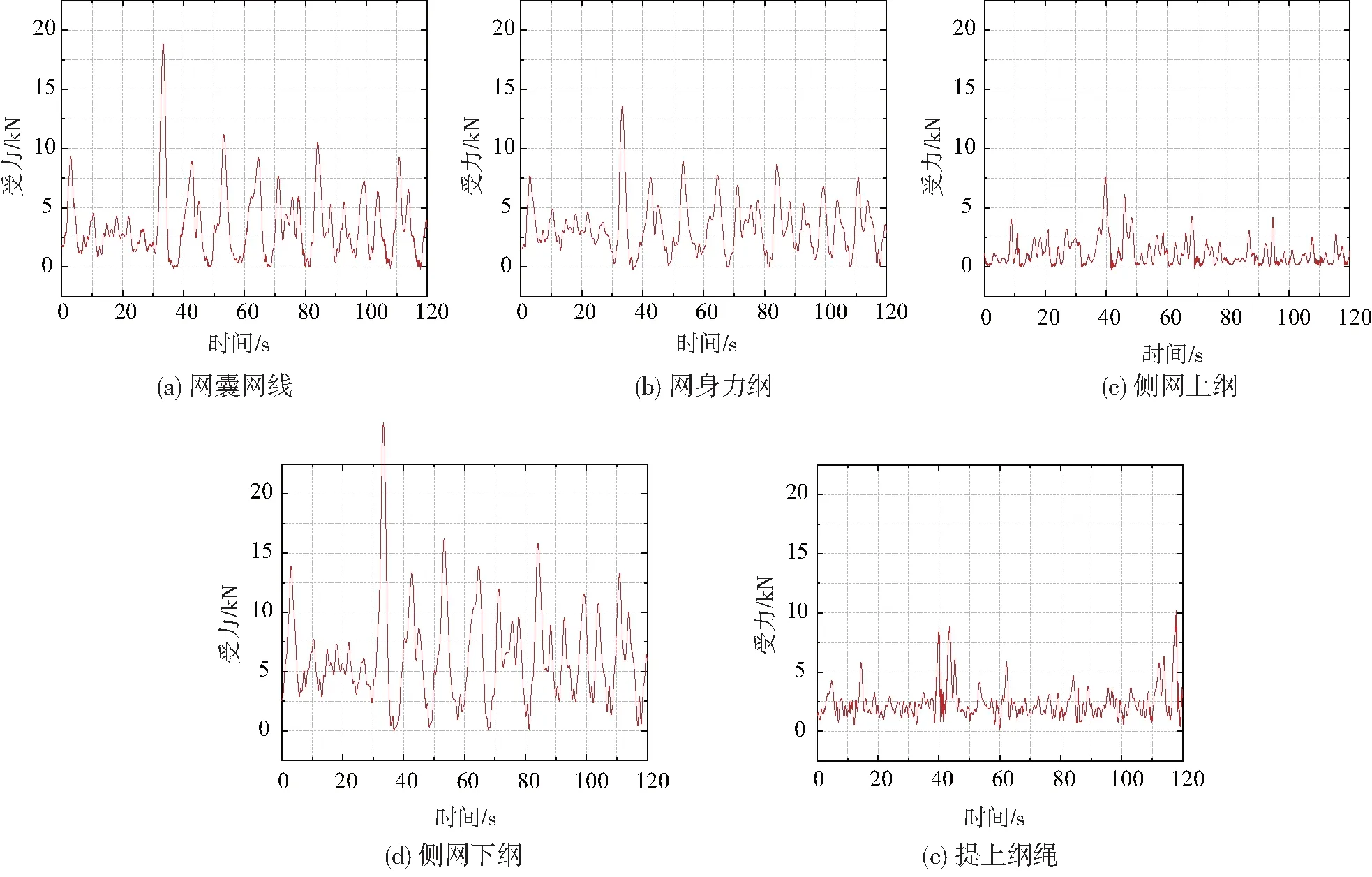
图11 网具各部位受力时历曲线

图12 网具总受力及对应波面

由图12可知,网具总受力为121.11 kN。需指出的是,网具总受力为各个构件在时域上的叠加,虽然每个构件的极值基本出现在同一个波浪周期内,但时刻点并非完全重合。可以看出,网具受力与波幅有直接关系,波幅越高其受力越大,而受力极值也出现在最大波幅所在的一个波浪周期内。

5 结论

研究发现,浮体受到的横向力受浮体与船舶的横向间距影响较大,受浮体与船舶的纵向间距影响较小;浮体与打捞船存在一个较为平衡的横向位置,在该位置下浮体受船舶辐射扰流影响较小,便于打捞船高海况下开展打捞作业;网具受力情况与波幅正相关,波幅越高网具受力越大,网具受力极值出现在最大波幅所在的一个波浪周期内。本研究将打捞回收分解为打捞船与浮体的耦合计算以及打捞浮体与网具的耦合计算两部分,传递参数为浮体相对船舶的位置及浮体运动响应,假设浮体与尾部网囊无相对位移,这可能导致网囊兜住浮体后的形状与实际有所出入,若要考虑网囊兜住浮体后的变形,则涉及刚性固体与柔性弹性体在复杂流体环境下的多重耦合,后续将对此做进一步研究。