基于卡尔曼滤波的多波束渔用声呐波束稳定算法仿真及实现

王志俊,程 婧,魏 珂,李国栋

(中国水产科学研究院渔业机械仪器研究所,上海 200092)

渔用声呐是一种利用声波对周边海域内的渔业资源进行探测的渔业装备,近几十年来在海洋渔业中发挥了重要作用。多波束渔用声呐是一种新型渔用声呐,可同时产生几十甚至几百个水平波束,同时扫描360°范围内的海域,其探测效率显著高于传统渔用声呐。但是由于受到海上风浪以及渔船作业状态的共同影响,渔船的航姿在声呐收发周期内始终处于动态变化之中,导致渔用声呐波束的指向随之发生偏移,无法精确地照射到目标鱼群上,从而增大误差和漏检率,降低鱼群探测效果。为了抵消海浪的影响,需进行姿态补偿。

近年来不少学者提出了多波束声呐姿态补偿的方法。传统思路是通过机械方式进行补偿,例如李华等[1]提出根据船舶姿态解算出换能器基阵的三轴转动角度,再通过伺服系统驱动基阵的转动,保证基阵处于水平面。机械方式只适用于低频声呐,且响应速度慢、维护成本高。随着数字波束形成技术[2]的发展,出现了电子补偿的方式,即根据船舶姿态对声呐波束的三维指向角进行自适应地校正。一些多波束测深系统[3]通过在阵元之间加入额外的相移来补偿基阵的纵摇,这种方案实现起来较为简单,但只能补偿纵摇运动,无法实现三维波束稳定。罗宇等[4]提出了平面阵发射波束稳定方法,可以在三维方向控制发射波束的发射指向,但没有探讨接收波束的补偿方式。陈若婷等[5]提出了一种基于横摇稳定的接收波束稳定算法,采用了波达时刻的横摇修正和求解波达时刻合成波束指向角相结合的方法。该方法在多波束测深系统中能获得较好的精度,但是本研究针对的多波束渔用声呐具有更多波束,带来更大的计算量,因此该方法并不适用。

本研究根据多波束渔用声呐的特点采用了电子补偿的方案。首先分析了影响波束稳定误差的因素,然后将卡尔曼滤波和数字波束形成技术相结合,提出了一种新的三维波束稳定算法。该算法作用于接收波束和发射波束,能够同时补偿横摇和纵摇运动,并且在不提高硬件成本的前提下了降低了补偿误差。

1 仿真模型

1.1 船舶姿态变化规律

出于安全考虑,不建议渔船在较高海况下进行捕捞作业,本研究只针对四级及以下海况。通常以有义波高作为海况的指标[6-7],四级海况对应波高1.25～2.50 m。在海浪的作用下,船舶可能发生6种摇荡运动,包括横摇、纵摇、艏摇、纵荡、横荡和垂荡。本研究主要关注对波束指向性影响较大的横摇和纵摇运动。

杜一豪等[8]对不规则波浪作用下Wigley型船的运动响应问题进行了系统性地研究,该模型较为精确,但大多数参数与波束稳定算法关系不大。本研究重点是分析波束稳定算法性能,因此为简化分析,将船舶的横摇和纵摇角度分别用一定摆幅和周期的正弦信号来表征。当海浪与某个声呐波束的遭遇角为0°时,可认为仅有纵摇,横摇幅度为0;当遭遇角为90°时,可认为仅有横摇,纵摇幅度为0;当海浪与某波束的遭遇角为其他角度时,通过横摇、纵摇的相位差进行反映。

李积德[9]指出,横摇的周期只与船舶固有参数有关;王驰明等[10]认为横摇幅度与航速和海况有关,航速越低,横摇幅度越大,海况越高,横摇幅度越大。纵摇的周期基本稳定在波浪谱峰周期附近;纵摇幅度与航速和海况有关,航速越快、海况越高,纵摇幅度越大。李晨等[11]列举了不同海况下横摇运动的典型参数。杜一豪等[8]列举了不同海况下纵摇运动的典型值。本研究所模拟的场景为四级海况、航速8节,根据文献提供的典型值,设定横摇角和纵摇角的仿真区间为幅度-15°至15°,周期6 s。

1.2坐标系及坐标旋转

多波束渔用声呐的换能器通常为圆柱阵,包含N行、M列阵元,形成S个扇区。通过数字波束形成算法,每个扇区产生一系列波束,S个扇区共同覆盖-180°～+180°水平方位。

首先建立大地坐标系,3个轴X、Y、Z分别指向正北、正西和垂直向上;再建立载体坐标系,以船艏方向为X正半轴、左舷方向为Y正半轴,Z轴方向遵循右手定则。最后建立扇区坐标系,由于本声呐采用电扫描方式,因此载体与换能器基阵的位置关系是固定的,对于第1扇区,其坐标系与载体坐标系重合,扇区中心指向船艏方向。其他扇区的坐标系分别为扇区1坐标系绕Z轴旋转相应角度。

为便于分析,假设静止状态下大地坐标系与载体坐标系重合(即船艏指向正北、左舷指向正西,如图1所示)。

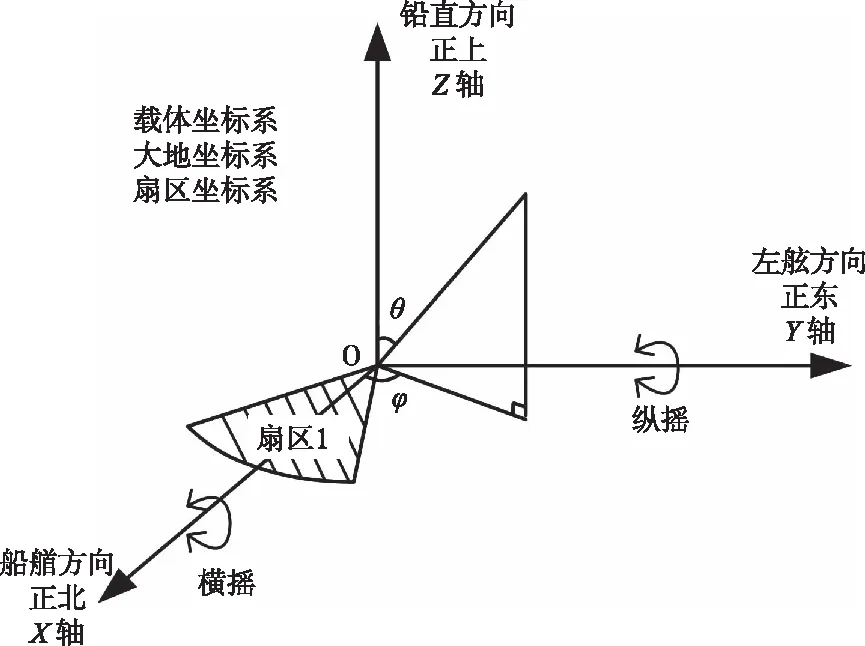
图1 三个坐标系

本研究主要分析海面起伏对扇区1各波束指向性的影响,以及波束稳定算法对扇区1各波束的补偿效果,其他扇区情况类似。

2 波束稳定算法流程

2.1 整体流程

波束稳定算法的整体流程如图2所示。

图2 波束稳定算法流程

每隔时间T读取姿态传感器的读数(横摇及纵摇的角度、角速度、角加速度),采用卡尔曼滤波器插值使姿态值的采样率提高1倍;通过坐标旋转及坐标变换计算出每个波束的目标指向角,最后通过数字波束形成技术产生相应的声呐波束。

2.2 卡尔曼滤波器插值

卡尔曼滤波器对横摇、纵摇姿态值分别做插值,以横摇为例,图3为单次卡尔曼滤波过程。

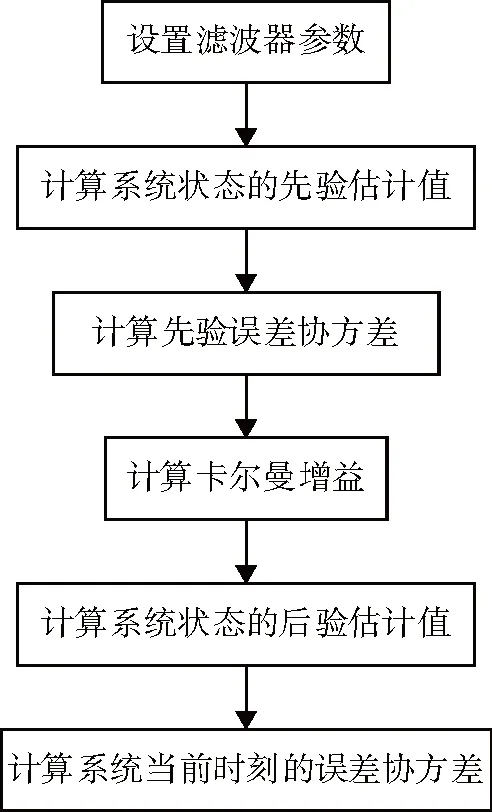
图3 卡尔曼滤波过程

首先初始化卡尔曼滤波器参数。观测矩阵H=I3(I3表示3阶单位矩阵);系统噪声Q服从均值为0、方差为σ的正态分布[12](为便于分析,取σ=0.1);测量噪声R服从均值为0、方差为0.1的正态分布(与姿态传感器的动态精度有关)。然后,每隔Δt=0.05 s进行一次迭代。第k次迭代过程如下:

(1)

将横摇、纵摇的后验估计值分别输出,即为第k次迭代的卡尔曼滤波插值结果(θkal,φkal)。

2.3 坐标旋转

设船舶在静止水面下的倾角为(θ0,φ0),根据卡尔曼滤波插值结果,计算出船舶相对于静止状态的估计偏移角度(Δθ,Δφ):

(2)

相当于扇区坐标系先绕X轴旋转Δφ,再绕Y轴旋转Δθ。式(3)为对应的旋转矩阵:

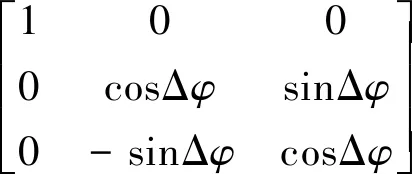
(3)

波束形成算法的目标波束指向角是相对于扇区坐标系而言的,因此各波束相对于大地坐标系的指向角会随着扇区坐标系的旋转而发生偏移。为补偿这种偏移,需将目标波束指向角乘以旋转矩阵A的逆:

A-1=AT=

(4)

(4)式利用了正交矩阵的性质。

2.4 计算补偿后的波束指向角

假设波束n相对于扇区坐标系的目标指向角度为(θn,φn)(球坐标系),则其对应笛卡尔坐标系的方向向量为An(xn,yn,zn),其中:

(5)

船舶存在姿态偏移的情况下,为使波束n相对于大地坐标系的指向不变,需通过如下变换矩阵进行反向旋转:

Anc=A-1·An=(xnc,ync,znc)

(6)

经过波束稳定处理后,波束n相对于扇区坐标系的指向角为Anc,将其转换回球坐标:

(7)

最后,采用程婧等[2]提出的数字波束形成方案,根据指向角(θnc,φnc)产生补偿后的声呐波束n。

3 波束稳定算法仿真

3.1 误差来源

由于波束稳定计算延迟、姿态仪更新间隔、姿态仪测量精度、船舶与海浪的遭遇角等因素影响,波束稳定补偿后的指向角与理想角度之间存在误差,算法设计的目标是指向误差不超过±1.8°。测量精度已反映在卡尔曼滤波器的测量噪声R中,以下分别讨论计算延迟、更新间隔、遭遇角等因素对指向误差的影响。

以指向-45°的波束为例,图4分析了纵摇角度与其指向误差的关系,其它波束以及横摇的情况与此类似。由图4可见,纵摇过零点时的瞬时角速度最大,计算延迟和更新间隔引入的误差最多,因此指向误差达到峰值。纵摇达到峰点或谷点时,瞬时角速度为零,计算延迟和更新间隔引入的误差也为零。

图4 纵摇角度与指向误差的关系

3.2 计算延迟的影响

多波束声呐的每个扇区往往要产生几十个波束,对于每个姿态值都需要计算所有波束的补偿值,运算量较大,因此必须考虑声呐软件的计算延迟。图5分析了更新间隔0.2 s、其他因素不变的情况下,计算延迟对波束稳定误差的影响。

图5 计算延迟对误差的影响

图中误差曲线由上下两部分组成,随着计算延迟的下降,误差峰值的下半部分由1.47°降低至0.3°,但上半部分没有明显改变。可见误差峰值的下半部分是由计算延迟引入的,而上半部分由其他因素引入。考虑到实际情况,软件计算延迟最低只能达到0.02 s,此时峰值误差为3.2°,不能满足设计目标。

3.3 姿态值更新间隔的影响

姿态传感器的姿态更新频率受限于接口速率以及姿态传感器本身的性能,性能越高的传感器越昂贵。渔用声呐所使用的姿态传感器通常性能一般,并且采用RS232或RS485接口,更新速率较低。考虑到姿态传感器的实际性能,设定最小更新间隔为0.10 s。图6分析了计算延迟固定为0.02 s、其他因素不变的情况下,姿态值更新间隔对误差的影响。

图6 更新间隔对误差的影响

根据前文分析,误差峰值的下半部分由计算延迟引入,固定为0.3°;随着更新间隔的降低,误差峰值的上半部分由2.9°降低至1.45°,此时总的峰值误差为1.75°。图7为整体变化趋势。

图7 整体变化趋势

其中更新间隔分别为0.30 s、0.20 s、0.10 s,计算延迟由0.10 s降低至0.02 s,可见最大误差角度随着更新间隔和计算延迟的降低而下降。当计算延迟为0.02 s时,误差主要由更新间隔导致,而由于传感器性能限制,更新间隔无法进一步下降,因此需对姿态参数做插值,并利用卡尔曼滤波器进行平滑处理。

3.4 卡尔曼滤波插值前后对比

接着采用卡尔曼滤波器对原始姿态值(包括角度、角速度、角加速度)做插值,使姿态值之间的时间间隔变为0.05 s,按照插值后的姿态值对指向-45°的波束进行补偿。插值前后的指向误差如图8所示。

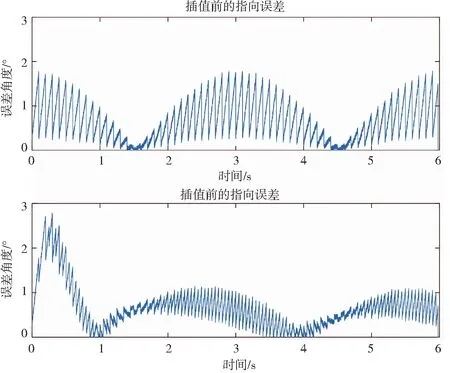
图8 卡尔曼滤波插值前后的指向误差对比

根据图8,卡尔曼滤波器的收敛用时约1 s(时长与滤波器参数有关),收敛后的指向误差由插值前的1.75°降低为1.18°。可见,卡尔曼滤波插值在不提高姿态仪更新间隔的情况下显著降低了波束稳定误差。

3.5 海浪遭遇角对波束稳定的影响

当海浪与波束指向的遭遇角不为0°时,可以将其分解为绕X、Y轴的摇晃。

指向误差与相位差的关系如图9所示。

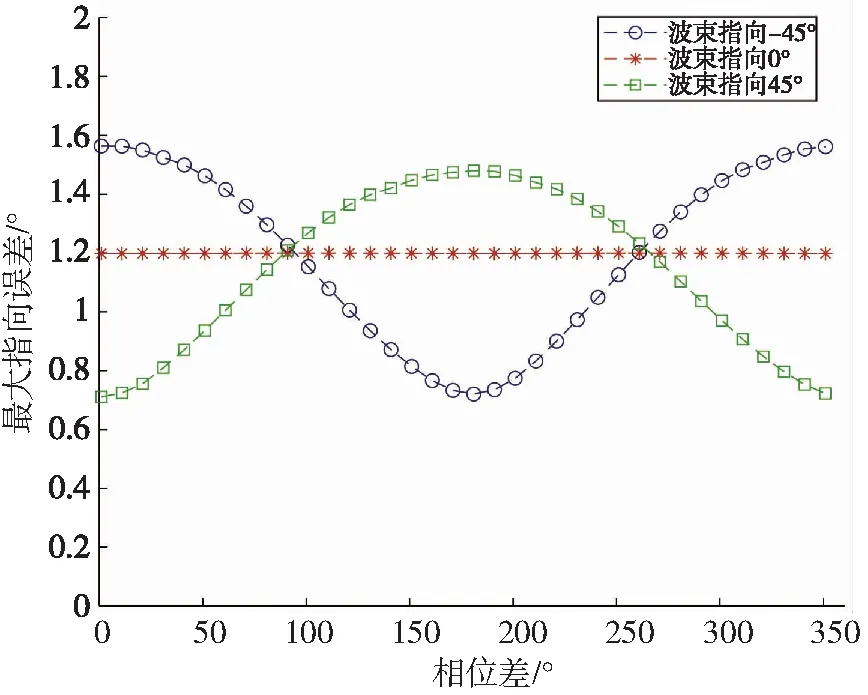
图9 指向误差与相位差的关系

多波束渔用声呐的一个扇区通常覆盖90°的水平角度,而扇区1的中心与X轴重合,因此其各个波束在-45°～45°之间均匀分布。以下将改变X、Y轴摇晃的相位差,分析其对各个波束插值后的补偿误差的影响;仿真时设定姿态更新间隔为0.1 s、计算延迟0.02 s;X、Y轴摇晃幅值均为15°,周期均为6 s。

可见当波束指向-45°,横摇、纵摇相位差0°时,指向误差出现最大值1.55°;相位差180°时,指向误差出现最小值0.75°。当波束指向0°,指向误差固定为1.2°,与横摇、纵摇相位差无关。当波束指向45°,横摇、纵摇相位差180°时,指向误差出现最大值1.5°;相位差0°时,指向误差出现最小值0.7°

4 试验测试

4.1 系统组成

为降低计算延迟,本系统基于FPGA(现场可编程门阵列)进行实现。其中,485接口模块用于初始化VG600姿态仪,并且每隔0.1 s读取一次姿态值(包含角度、角速度、角加速度);卡尔曼滤波模块对姿态角度做1倍插值;补偿模块每隔0.05 s根据插值后的姿态值进行补偿,依次计算出每个波束的补偿后指向角度(θnc,φnc),该指向角度同时作用于接收链路和发射链路;发射波束形成模块按照上述指向角度产生发射波束,并驱动换能器基阵进行发射;接收波束形成模块从换能器基阵获取接收数据,按照上述指向角度产生接收波束。多波束渔用声呐系统如图10所示,图中省略了收发链路信号处理模块。

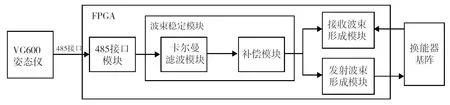
图10 多波束渔用声呐系统框图

4.2 测试原理

搭建了图11所示的测试系统,该系统由FPGA板卡、VG600姿态仪、MRU5姿态仪、上位机软件等组成。其中FPGA内部实现了多波束渔用声呐系统;VG600是本系统实际使用的姿态仪,更新间隔0.1 s,动态精度0.1°;MRU5是作为参照的高精度姿态仪,更新间隔0.05 s,动态精度0.02°。

图11 测试系统示意图

现场图片如图12所示,摆台绕X轴做幅度15°、周期6 s的正弦摆动,模拟船舶的横摇;绕Y轴做幅度15°、周期6 s的正弦摆动,模拟船舶的纵摇。FPGA每隔0.1 s读取VG600的姿态参数,每隔0.05 s进行一次波束稳定计算,并通过串口输出卡尔曼滤波结果及补偿后的波束指向角。与此同时,MRU5输出其测定的姿态角。上位机软件将补偿后的指向角按照MRU5提供的标准姿态角作姿态旋转,计算旋转后的指向角与波束的目标指向角之间的误差。

图12 现场图片

4.3 仿真与测试结果对比

4.3.1 卡尔曼滤波器插值结果对比

使摆台做幅值为15°、周期为6 s的纵摇(横摇同理);对于姿态角和卡尔曼滤波结果,分别对比其仿真值与实测值,结果如图13所示;可见二者幅值基本一致,插值后姿态值的更新间隔由0.10 s变为0.05 s。

图13 卡尔曼滤波插值结果对比

4.3.2 纵摇指向误差对比

摆台做幅值为15°、周期为6 s的纵摇(横摇同理),对各波束补偿后的指向误差进行了测试,并与各波束在更新间隔0.10 s、计算延迟0.02 s下的仿真结果对比,结果如图14所示。对于指向-45°、0°、45°的波束,实测最大指向误差分别为1.20°、0.70°、0.65°。与卡尔曼滤波器收敛后的仿真结果相比,实测的指向误差略大一些。

图14 不同波束的指向误差对比

仿真所采用的系统噪声的方差为经验值,可能与实际值有差异;作为参考的高精度姿态仪MRU5与被测姿态仪VG600在安装时存在位置偏差,以上因素可能导致指向误差偏大。

4.3.3 不同相位差下的指向误差对比

为对比不同相位差下的指向误差,令摆台同时做幅值为15°、周期为6 s的纵摇和横摇,相位差依次为0°、40°、…、320°,分别对指向-45°、0°、45°的波束进行测试,并记录最大指向误差。

实测值与仿真值对比如图15所示。实测误差比仿真误差大0.2°左右(原因如4.3.2节所述),各个波束在不同横摇纵摇相位差下的最大误差不超过±1.8°,符合波束稳定算法的设计预期。

图15 不同相位差下的指向误差对比

5 讨论

Marszal等[13]对多波束声呐的三维波束补偿进行了理论分析,并估算了W个波束情况下的计算量,但没有考虑到实际应用场景中的误差。本研究指出,即使经过波束稳定补偿后,多波束渔用声呐的波束指向角仍然存在误差,而这些误差主要来源于计算延迟和姿态值更新间隔。因此,本研究提出了一种基于FPGA的波束稳定处理架构,利用FPGA的并行计算能力大大提高了计算速度,实测计算延迟约为0.019 s。同时,本研究还采用了基于卡尔曼滤波的姿态插值算法,使姿态值更新间隔降低了50%。

另一方面,陈若婷等[5]在多波束测深仪中增加接收阵横摇稳定,使合成波束的指向误差范围由±5°降低至±0.5°;相比之下,本研究提出的波束稳定算法将多波束渔用声呐的指向误差范围从±15°降低至±1.8°,误差略大于前述方法。然而由于多波束渔用声呐的水平波束间隔典型值为2.25°[2],应用本方法后的误差范围小于波束间隔;此外,本研究在仿真参数和摆台测试参数的选择方面考虑了最恶劣的情况,测试平台也引入了一定的误差,在正常的渔业捕捞作业中,可以获得比±1.8°更低的指向误差。因此本研究具有较高的实用价值。

6 结论

多波束渔用声呐的波束稳定算法能够有效降低海浪波动对声呐波束指向性的影响,在四级海况下,可保证补偿后的波束指向角度最大偏差不超过±1.8°,从而显著提高渔用声呐在海上作业时的鱼群探测能力。本算法模块已成功应用在某型全方位多波束渔用声呐中。