立式V型曲面开缝网板的水动力性能数值模拟研究
徐 波,袁军亭
(上海海洋大学 工程学院,上海 201306)
0 引言
网板是单船拖网作业的最主要属具,其水动力性能的优劣,关系到网板的扩张性能,是影响渔获量与捕捞效率的重要因素,直接影响到网板的渔获性能与经济效益[1~5]。随着计算机软件技术的发展,计算流体动力学(CFD)作为一种研究网板水动力性能的数值仿真方法应运而生[1,6,7]。CFD能够研究网板的工作性能,更重要的是能够在节省时间、成本的情况下仿真复杂的工作状况[8]。因此,CFD被广泛应用于三维结构体的流体动力学分析,如,船结构的设计和人工鱼礁的外形设计[9]。Yelland[10]等用CFD研究船上部结构所受的风应力;percival[11]等用CFD优化了船的外壳。Takahashi[8]等用CFD在与水槽实验相同条件下对双翼型网板进行水动力性能分析,其分析结果与水槽实验结果吻合。XU Qingchang[12]等用两种数值仿真方法研究矩形V型网板,发现展弦比设定为0.49、反角设置为17°时,网板展现出更好的水动力性能。XU Qingchang[13]等用数值仿真方法评价全尺寸矩形网板的水动力性能,其结果正确地印证了先前的水槽实验结果。XU Qingchang使用风洞实验、水槽实验与数值仿真分别研究双导流板矩形曲面网板,结果表明风洞实验与水槽实验结果分别与各自的数值仿真结果吻合[14]。以上可鉴,CFD仿真方法是一种强有力的网板水动力性能研究方法,本文运用Fluent19.2研究立式V型曲面开缝网板的水动力性能。
1 数值模型
1.1 控制方程
网板数值仿真过程中,假设流体不可压缩、各向同性,控制方程包括:
1)连续性方程

2)N-S方程

1.2 参数定义
描述网板水动力特性的参数主要有雷诺数Re、升力系数CL、阻力系数CD、升阻比K。
1.3 模型参数设置
网板计算域如图1所示,水的密度为998.2kg·m-3,动力粘度μ为0.001003kg·m-1·s-1[8,15],计算域边界划分如图2所示,计算域的左端面设置为速度入口,右端面设置为压力出口,下端面设置为无滑移壁面,其余三面设置为自由滑移壁面[8,16]。水流方向沿x轴正方向均匀流动,湍流强度为5%,回流湍流强度为5%,回流湍流粘性比为10,湍流粘性比为10[12]。

图1 网板流体动力学分析计算域
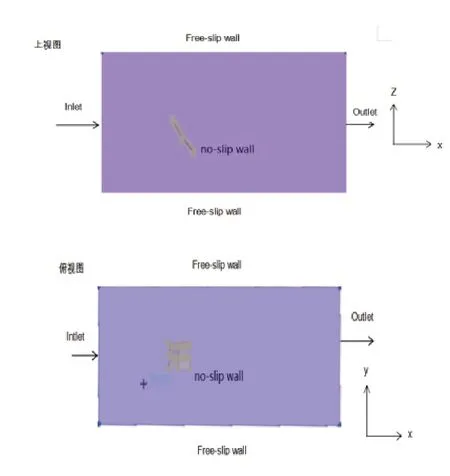
图2 计算域边界条件设置
1.4 数值计算方法
湍流模型选择k-epsilon模型,控制方程采用有限体积法进行离散,瞬态方程采用第一顺序隐式,计算步长为1s,计算步数设置为1000步。数值仿真参数设置[8,12,14,16,17]如表1所示。

表1 数值仿真参数设置
2 材料与方法
2.1 全尺寸网板
本文是对立式V型曲面开缝网板全尺寸进行数值仿真研究,网板是由不锈钢制成,网板主要结构包括翼展、翼弦与开缝,其中网板上设置开缝结构,网板背部涡流受到较大的水流冲击,可以达到改善背部流态、减少阻力的作用,提高网板的水动力性能[1,18,19]。主要尺寸翼展为4.02m,弦长为2.36,展弦比(AR)为 1.7,曲面率为23%,总面积约为9.22m2。如图3所示是网板的三维结构与网板的非结构化网格划分结构[13]。

图3 网板三维结构(左)和网板三维网格结构(右)
2.2 全尺寸网板的数值仿真
本文使用软件ANSYS19.2的FLUENT对网板进行数值仿真,FLUENT在模拟仿真网板周围的速度场更加精确[14]。在计算过程中,利用有限体积法解决雷诺-平均纳斯维托克斯方程(N-S方程)[13]。计算模型选取标准的k-ε湍流模型改进的可实现的k-ε湍流模型进行网板流体仿真[13]。
网板的计算域通过分别调整长度、宽度与高度进行确定,采取的方法是一步一步地分别增加或减少计算域的长度、宽度与高度改变计算域体积,通过流体仿真进行残差值计算,残差图如图4所示,如图1所示的计算域是残差图收敛的情况下所确定的计算域[13]。由于网板在海域中底层工作,计算域的底面设置为无滑移壁面,其余面除了速度入口与压力出口以外,均设置为自由滑移壁面,网板的计算域分别被设置为15L、8L和5L,网板距离底面3L(L为网板翼展,L=4.02m),网板距离水流入口端面2L,计算收敛精确度相对误差小于1%[13]。

图4 残差图(收敛)
网板周围的计算网格如图5所示,网板的网格以非结构化形式划分,网格单元的最小体积为0.1mm3以上,网格质量良好。网板及其他边界采用局部加密的方式不断验证网格的可行性,保证网格单元的最小体积大于0.1mm3,最终取得计算精度较好的非结构化网格。网格的总单元数量约为2.8×106,节点数约为5.1×105。
边界设定情况如图2所示,入口边界设定为速度入口,速度设置为0.4m/s~1m/s,速度增量设置为0.15m/s;出口边界设定为压力出口,相对压力设置为0Pa[12]。在仿真过程中,AOA(冲角)的范围为10°~90°,增量为5°[13,20]。
2.3 数据处理
网板的升、阻力系数可以根据式(2)、式(3)进行计算,其中FL和FD由仿真得出相应的数值。计算公式如下:

式中:v 为来流速度(m/s),b 为网板弦长(m),ρ为流体密度(kg/m3);μ为流体实际的动力粘度(kg/m•s);FL为网板扩张力(N),即网板所受的升力;FD为网板阻力(N);S为网板总面积(m2)。

图5 板网周围的计算网格示意图
升力FL是与来流方向垂直的分力,阻力FD是与来流方向平行的分力,升力系数CL与扩张力同阻力的比值K是衡量网板水动力性能的重要参数[1],两者的值越大,对网板的水动力性能越有利。如图6所示F为网板受到的总作用力,其水平分力为阻力FD、垂直分力为升力FL,α为冲角,V为来流速度。

图6 网板受力与来流方向
3 全尺寸网板的仿真结果
3.1 全尺寸立式V型曲面开缝网板的水动力性能
如图7所示为不同速度下影响全尺寸立式V型曲面开缝网板水动力性能的升力系数、阻力系数及的升阻比随冲角的变化形成的曲线趋势图,图7表明5种速度下的升力系数、阻力系数、升阻比曲线图没有明显的变化,说明速度对网板的水动力性能影响甚微。阻力系数随着冲角的增加而增加,升力系数与升阻比随着冲角的增加呈先上升后下降的趋势。当冲角α为45°时,升力系数取得最大值,如表2所示是入口速度分别为0.4m/s、0.55m/s、0.70m/s、0.85m/s与1m/s所对应的最大升力系数。5种速度状况下升力系数曲线均表明当冲角α为45°时,网板的升力系数取得最大值,所以45°是立式V型曲面开缝网板临界冲角,此时网板的扩张性能最好。网板的升阻比随着冲角的增加先上升后下降,如表2是不同速度下所对应的最大升阻比,图7的升阻比曲线图表明升阻比在冲角α为20°时,取得最大值,此时网板的工作效率最高,表2数据表明5种速度情况下的最大升力系数与最大升阻比没有显著的变化,可以得出结论:速度对网板的水动力性能影响很小。由立式V型曲面开缝网板的升力系数与升阻比曲线图得知此网板的工作冲角范围很大,冲角在35°~45°范围内升力系数与升阻比数值均处于较高值,网板的水动力性能良好,渔网的水平扩张性能很好,建议网板的工作冲角范围为35°~45°。网板在35°~45°有更大的升力系数与较小的阻力系数,此范围内网板的水平扩张性能好,这也验证了Xu BS[21]等发现V型曲面网板与其他网板相比在水平扩张与总捕获量上有更大的优势。

表2 不同速度的最大升力系数与不同速度的最大升阻比
3.2 网板周围的流线分布

图7 升力系数与阻力系数(上),升阻比(下)(入口速度为 0.4m/s~1m/s)随冲角变化曲线
如图8所示为立式V型曲面开缝网板在入口速度为1m·s-1的二维流线型可视图与涡流核心区域图(涡流核心区域图显示的是漩涡区域),流线型视图皆是取自切于网板中部水平板面的流线图,涡流核心区域图是相同冲角所对应的涡流状态图。图中所示在冲角为10°时,网板的前缘背流面流线出现了分离,在α为15°~40°,流动分离逐渐向网板的后端发展,网板两面(压力面和背流面)的流线逐渐变得集中。在α为45°时流动完全分离,网板出现了失速现象。在冲角大于45°的情况下,漩涡开始散布,从网板前端向后缘移动,分离点移到网板的后缘,漩涡在尾迹区完全形成,更多的漩涡形成并逐渐扩散,流线保持分离的状态。网板的升力由压力差与翼尖涡流[22]诱导形成,涡流图表明翼尖漩涡在较小的冲角(10°~40°)逐渐形成,翼尖漩涡的区域逐渐增加,在冲角为45°流动完全分离后,翼尖涡流区域开始扩散,之后逐渐坍塌,升力系数开始下降。在冲角大于45°后网板的背流面上部可以观测到更大的翼尖漩涡[23],在冲角为65°~80°逐渐发展。在冲角为85°时网板背流面由一个漩涡形成了两个漩涡,即双子涡[23],在冲角为90°时,双子涡完全形成。通过数值仿真验证,其他入口速度下的网板状态在流线型与涡流核心区域图与速度为1m/s有相同的结果,表明立式V型曲面开缝网板在不同的速度状态下有相同的水动力性能,进一步论证了速度对网板的水动力性能影响甚微。由涡流核心区域图表明从冲角10°~45°网板的前端和后缘漩涡云图逐渐分离,从原来冲角为10°时前端与后缘的漩涡云图在网板中部水平板面相互重叠到冲角为45°出现完全分离,在冲角45°之后持续分离,进一步表明网板在冲角45°出现了失速现象。

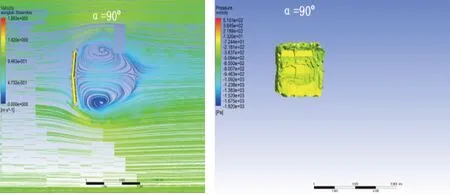
图8 网板周围流线型(2d)分布(左)和涡流核心区域图(右)
4 结语
立式V型曲面开缝网板的水动力性能曲线表明当冲角为45°时,网板有最大的升力系数,冲角为20°时,升阻比取得最大值,冲角为20°时网板取得了最大的升阻比,较大的升阻比出现在较小的冲角值的情况下,网板的升力系数在较小的冲角值的情况下非常小,冲角为45°时,网板的升阻比相对较大,因此45°是最佳工作冲角。
根据Balash等[24]建议蝙蝠翼型网板的工作冲角为20°时水动力性能良好,建议立式V型曲面开缝网板工作冲角为35°~45°,此时网板工作效率(发生在较低的冲角)高、有效性(发生在较高的冲角)都比较高。涡流图表明冲角10°~45°,网板背流面的流线逐渐的集中在一起,网板翼尖漩涡的区域越来越大,逐渐散布,流动分离程度越来越大,在冲角45°后,翼尖漩涡向网板后端扩散开,网板背流面的流体流动完全分离,出现了失速现象,不利于网板进行捕鱼。
立式V型曲面开缝网板水动力性能比矩形网板更好。如图9所示,XU Qingchang[25]等对矩形网板进行模型实验,得到的升力系数与阻力系数在冲角10°~50°的变化曲线,其变化趋势与图7相同,相比之下,XU Qingchang研究的矩形网板在冲角40°时取得最大升力系数,表明40°为最佳工作冲角,立式V型曲面开缝网板具有较大的最佳工作冲角、较大的升力系数与较大的工作冲角范围。
立式V型曲面开缝网板的水动力性能优于矩形V型网板。如图10所示,XU Qingchang[12]等对矩形V型网板进行水动力性能模拟实验,得到的升力系数与阻力系数在冲角10°~60°的变化曲线,其变化趋势与图7和图9相同,在冲角40°取得最大升力系数,表明40°为矩形V型网板的最佳工作冲角,而立式V型曲面开缝网板的最佳工作冲角为45°,最大升力系数远远大于矩形V型网板。
文中全面地对立式V型曲面开缝网板的工作冲角进行了研究分析,得到了网板的最佳工作冲角与升力系数、阻力系数随冲角的变化曲线。但是,网板在捕鱼的工程中,水中环境极其复杂,文中并没有考虑到海底及其他事物对网板的摩擦力对网板的影响,在以后的研究过程中应逐步考虑进去,以减少误差。

图9 升力系数随冲角的变化曲线(左),阻力系数随冲角的变化曲线(右)

图10 升力系数、阻力系数与冲角的变化关系
5 结语
通过数值仿真模拟的方法对立式V型曲面开缝网板进行水动力性能研究,研究结果对于分析网板的水动力性能提供了依据,分析表明立式V型曲面开缝捕鱼网板比矩形网板与矩形V型网板水动力性能更好,同时为以后的研究奠定了基础。基于这些仿真结果,提高了立式V型曲面开缝捕鱼网板的使用技能,有利于提高网板的渔获效益。

