摩擦因数与弹丸形变对超声喷丸纯铜的影响研究*

陶欣荣,王 成,2*,钟 瑶,周 彬,黄海泉,苏 奇

(1.安徽理工大学 机械工程学院,安徽 淮南 232001;2.高端激光制造装备省部共建协同创新中心,浙江 杭州 310023)

0 引 言

对于某些服役状态下的机器而言,由于承受复杂交变载荷,其机械零部件表面很容易产生疲劳裂纹,进而引起零部件的失效[1-3]。

喷丸强化可以在受喷零部件表面注入有益的残余压应力场,有效抑制疲劳裂纹的萌生和扩展,显著延长机械零部件的服役寿命[4-6]。

超声喷丸是一种新型的喷丸强化技术。它利用超声发生器产生高频电振荡信号(50 Hz～20 kHz),利用换能器将高频电振荡信号转换为机械振动,再采用变幅杆将机械振动的幅值放大(10 μm～100 μm),并传递给振动工具头,进而驱动振动工具头上端的弹丸不定向重复冲击金属材料,诱导金属材料表层产生大量的弹塑性变形,实现材料表面改性的目的[7-9]。

近年来,为揭示超声喷丸强化机理和优化超声喷丸工艺参数,研究人员开展了大量的超声喷丸的数值模拟和实验研究。

KUMAR S等人[10]对TC4钛合金进行了超声喷丸处理,结果发现,试样表层产生的残余压应力能够显著提高材料的疲劳性能。PANDEY V等人[11]对2014铝合金进行了超声喷丸实验,结果发现,超声喷丸在材料表层形成的最大残余压应力可达到550 MPa,并使材料表面硬度提高了45%。YARAR E等人[12]采用单丸粒超声喷丸模型,研究了弹丸尺寸和速度对AA7075-T6力学性能的影响。王成等人[13]构建了一套耦合宏观超声喷丸模型与细观晶体塑性模型的多尺度计算框架,采用该框架,探究了超声喷丸纯铜诱导的晶粒细化和宏观、细观残余应力。罗鹏等人[14]基于超声喷丸42CrMo钢的有限元模拟,建立了超声喷丸工艺参数与材料表面残余应力、显微硬度和表面形貌之间的关系模型。ZHANG Y等人[15]创建了具有不同粗糙度振动头的多弹丸超声喷丸数值模型,借此研究了弹丸冲击角与冲击速度的变化规律。

相对于实验研究,数值模拟不仅周期短、成本小,而且能够定量分析超声喷丸强化机理。然而,在绝大多数的超声喷丸有限元模型中[16-25],研究者都将弹丸处理成刚体,忽略了弹丸的弹性、塑性变形对数值模拟结果所带来的影响。

另外,弹丸表面与受喷材料表面之间的接触通常采用罚函数法进行数值计算,摩擦因数是罚函数算法中的一个重要的控制变量。关于弹丸表面与受喷材料表面之间的摩擦因数对超声喷丸数值预测结果的影响规律,目前还鲜有报道。

针对上述问题,笔者以纯铜试样为研究对象,结合超声喷丸实验和数值模拟过程,研究摩擦因数与弹丸形变对超声喷丸纯铜的影响规律。

为消除多弹丸之间的相互作用对数值预测结果的影响,在超声振动驱动作用下,笔者只采用单个弹丸冲击纯铜试样;然后,建立单丸粒超声喷丸纯铜的三维有限元模型,创建刚性丸、弹性丸、弹塑性丸等3种不同类别的弹丸,以及设置0.1、0.2、0.3、0.4、0.5等5种不同的摩擦因数,以探究摩擦因数和弹丸形变对受喷纯铜试样表面形貌和残余应力的影响规律。

1 超声喷丸纯铜模型

1.1 三维有限元模型

基于超声喷丸强化工艺,笔者建立单丸粒超声喷丸纯铜的三维有限元模型。该有限元模型主要包含4个部分:纯铜试样、喷丸腔、弹丸和振动头。

笔者建立纯铜试样为长12 mm、宽12 mm、高3 mm的长方体模型,将其固定在喷丸腔的上端。喷丸腔内的长、宽、高均为12 mm,喷丸腔的壁厚为1 mm。为简便计算,将振动头建立成与纯铜试样尺寸相同的长方体模型,位于喷丸腔的下端。

笔者创建弹丸为直径6 mm的球体模型。初始状态下,弹丸位于喷丸腔内振动头上表面的中心位置。

由于喷丸腔壁和振动头的硬度要远高于纯铜试样的硬度,为提高计算效率,笔者将喷丸腔模型和振动头模型均处理成刚体,同时将喷丸腔刚体模型参考点的所有自由度锁定;在振动头刚体模型参考点上施加位移载荷,使其沿Z轴做超高频简谐振动(振动幅值为35 μm,振动频率为15 kHz)。

笔者分别创建弹丸表面-纯铜试样下表面、弹丸表面-喷丸腔内表面、弹丸表面-振动头上表面的接触关系,采用罚函数法计算它们之间的相互作用。

假设弹丸表面与喷丸腔内表面和振动头上面之间均无摩擦,笔者设置弹丸表面与纯铜试样下表面之间的摩擦因数分别为0.1、0.2、0.3、0.4和0.5,尝试探究摩擦因数对超声喷丸纯铜的影响规律。

单丸粒超声喷丸纯铜的三维有限元模型如图1所示。

图1 单丸粒超声喷丸纯铜的三维有限元模型

1.2 模型的材料参数

为进一步研究弹丸形变对超声喷丸纯铜的影响规律,笔者分别建立刚性丸、弹性丸和弹塑性丸等3种弹丸模型。其中,3种弹丸模型的质量密度均为7 800 kg/m3,弹性模量均为210 GPa,泊松比均为0.3。

笔者采用理想弹塑性模型来表征弹塑性丸冲击纯铜试样时自身产生的弹塑性变形。弹塑性丸的屈服强度为1 500 MPa[26]。

笔者采用三维八节点缩减积分实体单元(C3D8R/ABAQUS),对单丸粒超声喷丸纯铜的三维有限元模型进行网格划分。笔者采用网格敏感性试算,确定纯铜试样模型局部受冲击区域的细化网格尺寸为0.1 mm,网格数为392 000,节点数为417 501。

考虑到超声喷丸诱导金属材料的高应变率硬化效应,笔者采用Johnson-Cook模型表征纯铜试样在超声喷丸过程中的动态力学行为,其关系式可表示为[27]:

(1)

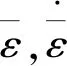
对于纯铜材料,Johnson-Cook模型的材料参数如表1所示[28]。

表1 纯铜Johnson-Cook模型的材料参数

2 喷丸模型的实验验证

2.1 超声喷丸纯铜实验

超声喷丸纯铜的实验装置图如图2所示。

图2 超声喷丸纯铜实验装置图

基于超声喷丸实验平台,笔者开展了单丸粒超声喷丸纯铜的实验研究,以验证超声喷丸纯铜有限元模型的有效性。

实验中,纯铜试样的几何尺寸为200 mm×40 mm×3 mm。在超声喷丸之前,笔者利用0.5 μm的金刚石抛光剂将待喷表面抛光成镜面(以便于观察弹丸冲击形成的凹坑形貌),并利用端盖,将纯铜试样固定在喷丸腔的上端,试样下表面距离振动头上面60 mm。

笔者在喷丸腔内放置一个直径6 mm的钢丸;设置超声振动的频率为15 kHz,振动头的振幅为35 μm,喷丸时间为5 s。

根据能量守恒定律,可计算弹丸冲击纯铜试样表面时刻的速度(vi)为:

(2)

式中:g为重力加速度,g=9.8 m/s2;H为纯铜试样与振动头之间的距离,H=60 mm;v0为振动头驱动弹丸运动的初始速度。

根据式(2),可以计算弹丸从冲击头上表面运动到纯铜试样下表面的速度变化率δ,即:

(3)

有限元计算所得弹丸速度如图3所示。

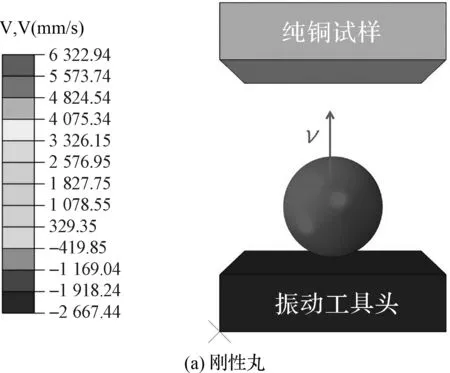
图3 弹丸初始速度的预测结果

基于有限元计算,笔者得到刚性丸、弹性丸和弹塑性丸的初始速度分别为6.3 m/s、5.5 m/s和4.9 m/s。因此,弹丸速度变化率的最大值不超过:δmax=9.8×0.06/4.92×100%=2.44%。

由此可见,对于单丸粒超声喷丸纯铜的实验而言,试样与振动头之间的距离(称之为“喷丸距离”)对有限元预测结果的影响很小,可以忽略不计。

弹丸冲击力演化如图4所示。

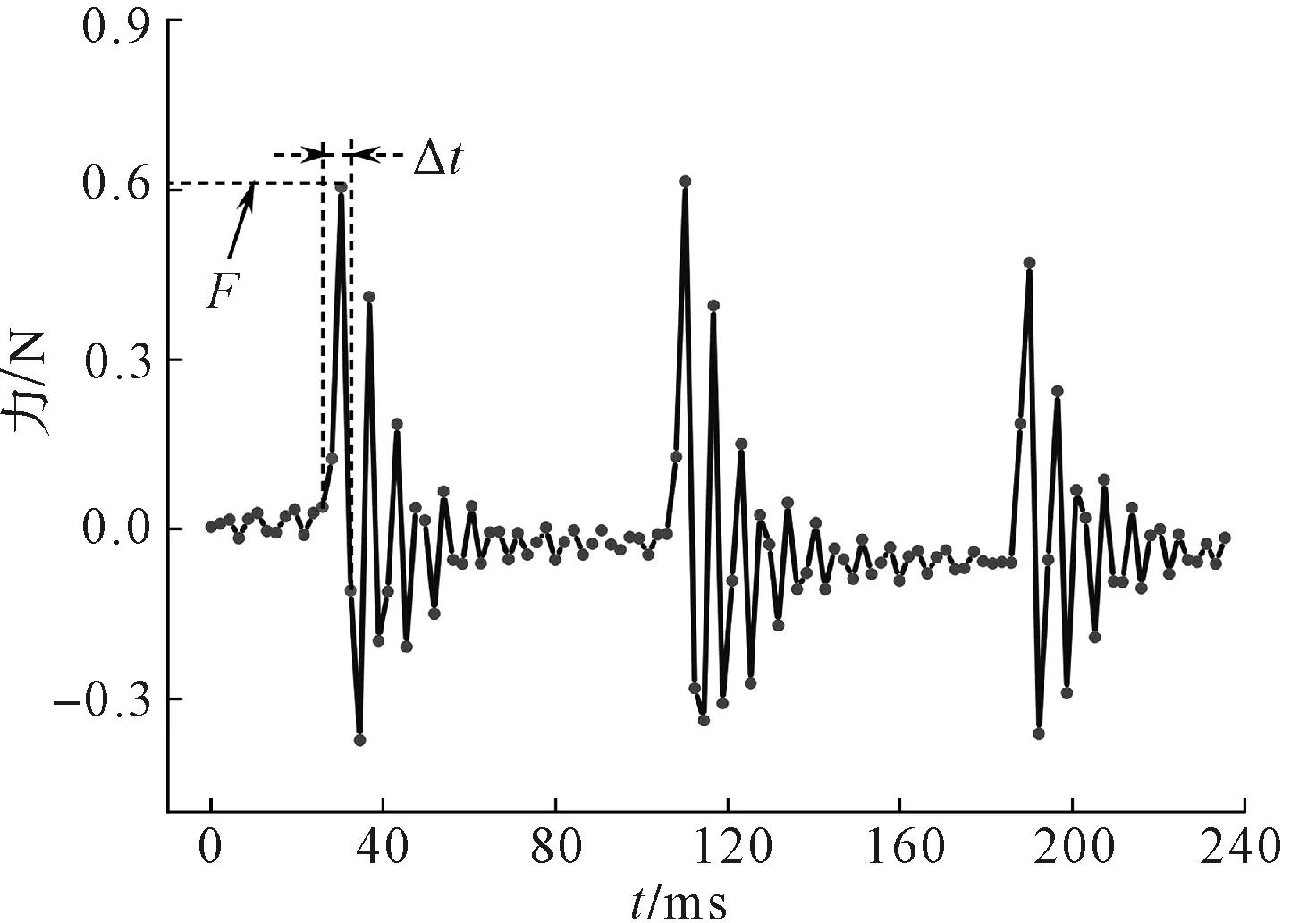
图4 弹丸冲击力的演化

笔者利用冲击力传感器测试超声喷丸过程中弹丸冲击力的演化。

由图4可知:当超声振动驱动弹丸冲击待喷表面时,受喷表面响应的冲击力迅速增大至一个峰值,然后随着弹丸的反弹离开而迅速减小。

此处传感器的采样频率选400 Hz。

笔者将冲击力迅速上升和迅速下降这两个阶段的累积时间看成Δt,假设在Δt范围内,冲击力的数值保持其峰值不变,则根据动量定理,有:

F·Δt=msvi-msvo

(4)

式中:ms为弹丸的质量,ms=0.882 g;vi,vo为弹丸的入射速度和反弹速度。

假设:1)弹丸冲击试样后静止,则vo=0 m/s,vi=(F·Δt)/ms;2)弹丸等速反弹,则vo=-vi,vi=(F·Δt)/2ms。因此,图4中,F=0.615 N,Δt=7.5 ms,可评估弹丸的入射速度vi∈(2.62 m/s,5.23 m/s),其显然与数值预测弹性丸和弹塑性丸的弹丸速度相近,由此可以验证超声喷丸纯铜有限元模型的有效性。

2.2 凹坑形貌测量

此处用于测量凹坑形貌的PS50型(NANOVEA)三维形貌仪,如图5所示。

图5 PS50型三维形貌仪

超声喷丸结束后,笔者利用PS50型(NANOVEA)三维形貌仪扫描纯铜试样受喷表面,得到了超声喷丸纯铜的测量结果,如图6所示。

图6 超声喷丸纯铜形成的凹坑形貌

由图6可知:超声波驱动单丸粒冲击纯铜形成的凹坑,与有限元模拟的凹坑相一致。

实验测试的凹坑形貌与数值预测结果的比较结果,如图7所示。

图7 实验测试的凹坑形貌与数值预测结果

笔者过凹坑中心做切面,得到凹坑形貌。由图7可见:有限元预测的凹坑形貌与实验测量结果具有很好的一致性。

该结果进一步验证了超声喷丸纯铜有限元模型的有效性。

3 结果与讨论

3.1 摩擦因数对数值预测结果的影响

3.1.1 凹坑形貌

笔者设置弹丸表面与纯铜试样下表面之间不同的摩擦因数为0.1～0.5。模拟超声喷丸纯铜形成的凹坑形貌,如图8所示。

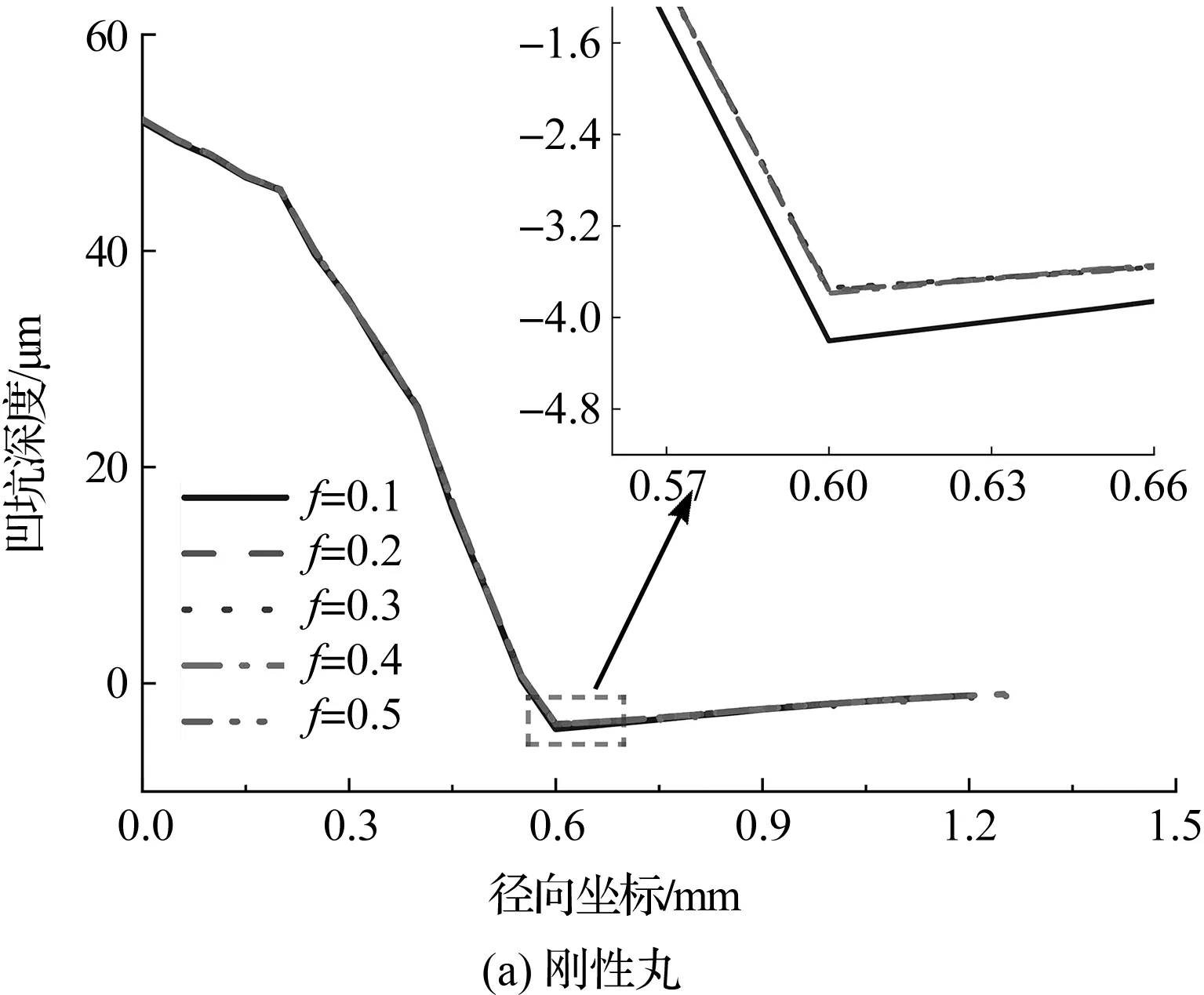
图8 超声喷丸纯铜形成的凹坑形貌

从图8中可以看到:

1)对于同一类型的弹丸而言,弹丸表面与纯铜试样下表面之间的摩擦因数,对超声喷丸形成的凹坑形貌的影响并不明显;2)另外可以发现,随着摩擦因数的增加,凹坑深度逐渐减小,并趋于稳定;当摩擦因数大于0.3时,凹坑深度不再随摩擦因数发生变化。

3.1.2 凹坑边缘凸起高度

不同摩擦因数下凹坑边缘凸起高度如图9所示。

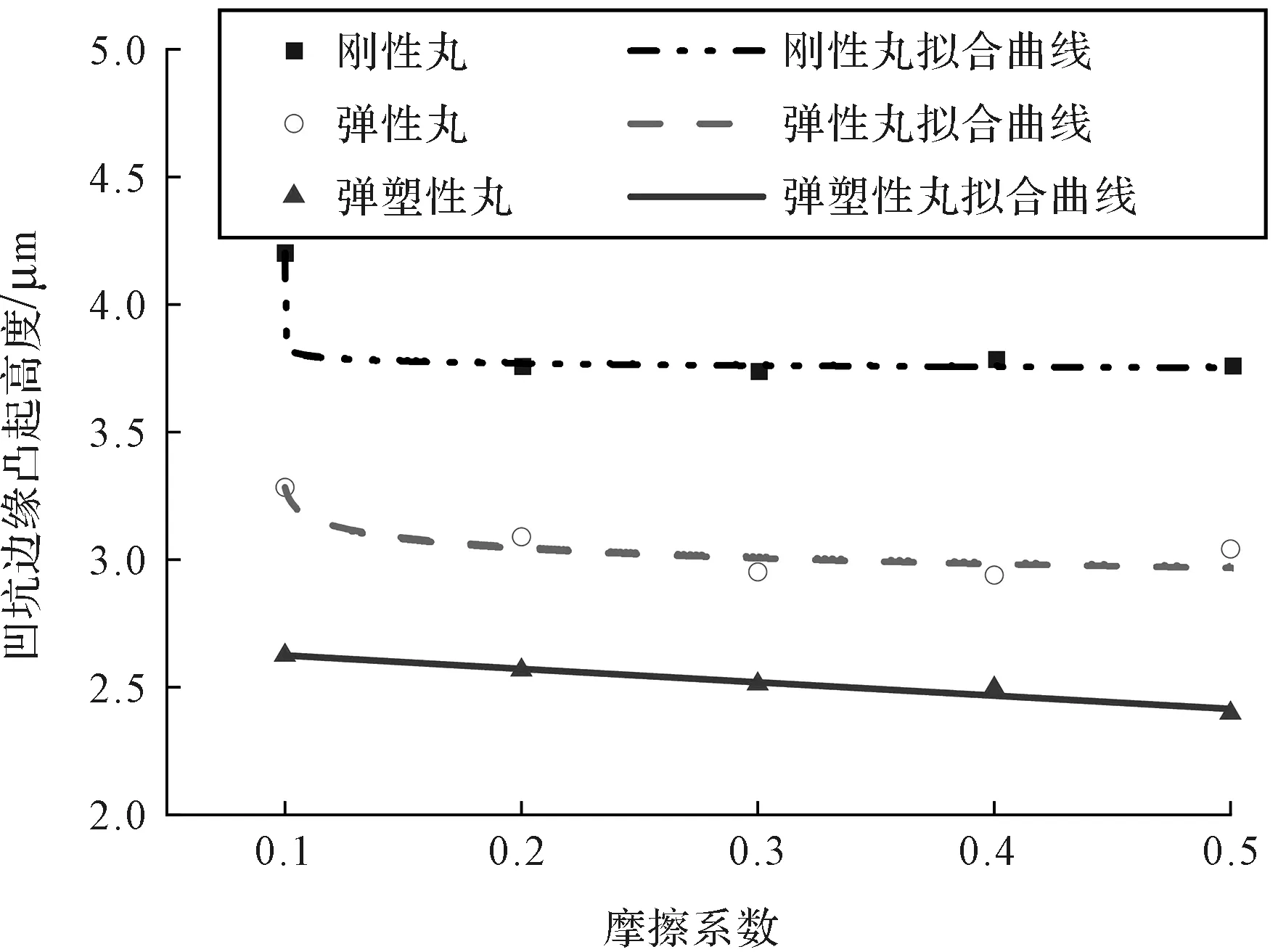
图9 摩擦因数对凹坑边缘凸起高度的影响

由图9可知:1)对于刚性丸和弹性丸而言,当摩擦因数大于0.2时,凹坑边缘凸起高度不再随摩擦因数的增加而减小;2)对于弹塑性丸而言,随着摩擦因数的增加,凹坑边缘凸起高度近似地呈线性减小。

3.1.3 残余应力分布

有限元数值预测超声喷丸纯铜的残余应力分布,如图10所示。

图10 有限元预测残余应力

由图10可知:不同摩擦因数工况下,超声喷丸纯铜诱导的残余压应力场主要位于凹坑的下方,最大残余压应力达到270 MPa,凹坑的边缘呈现残余拉应力状态。

笔者以凹坑中心为起点,沿纯铜试样的厚度方向建立一条路径,分析超声喷丸诱导纯铜的残余应力。

残余应力沿试样厚度方向的分布情况如图11所示。

图11 残余应力沿试样厚度方向的分布

由图11可知:随着摩擦因数的增大,刚性丸和弹性丸的表面残余拉应力和最大残余压应力均增大,并趋于稳定;但是弹塑性丸的表面残余拉应力和最大残余压应力均呈现先增大后减小的变化趋势;

从图中可以看到,不管对于刚性丸、弹性丸还是弹塑性丸,当弹丸表面与纯铜试样下表面之间的摩擦因数大于0.2时,超声喷丸纯铜诱导的残余应力对摩擦因数的增大不再敏感。

3.1.4 等效塑性分布

不同摩擦因数下,超声喷丸纯铜形成的等效塑性应变沿厚度方向路径的分布情况,如图12所示。

图12 等效塑性应变沿试样厚度方向的分布

由图12可知:超声喷丸诱导的残余应力场与受喷纯铜的塑性变形有关,等效塑性应变可表征材料的塑性变形。对于同一类型弹丸(刚性丸、弹性丸或弹塑性丸),当弹丸表面与受喷纯铜表面之间的摩擦因数大于0.2时,摩擦因数的增加不会使受喷纯铜的塑性变形再发生明显的变化,这与摩擦因数对超声喷丸诱导的残余应力的影响相一致;

相对于摩擦因数为0.1的工况,摩擦因数大于0.2工况的纯铜表层等效塑性应变明显偏小,这是因为摩擦因数的增加会导致受喷纯铜表层的塑性应变率增大,促进塑性区材料的应变率硬化,使得材料的塑性变形愈加困难,进而形成较小的等效塑性应变。

3.2 接触刚度对数值预测结果的影响

基于摩擦因数对超声喷丸纯铜数值预测结果的影响规律,笔者选择弹丸表面与纯铜试样下表面之间的摩擦因数为0.4;并且分别采用刚性丸、弹性丸和弹塑性丸冲击纯铜试样,研究弹丸形变对超声喷丸纯铜数值预测结果的影响规律。

3.2.1 不同材质弹丸的凹坑形貌

不同材质弹丸(刚性丸、弹性丸和弹塑性丸)冲击纯铜试样形成的凹坑形貌,如图13所示。

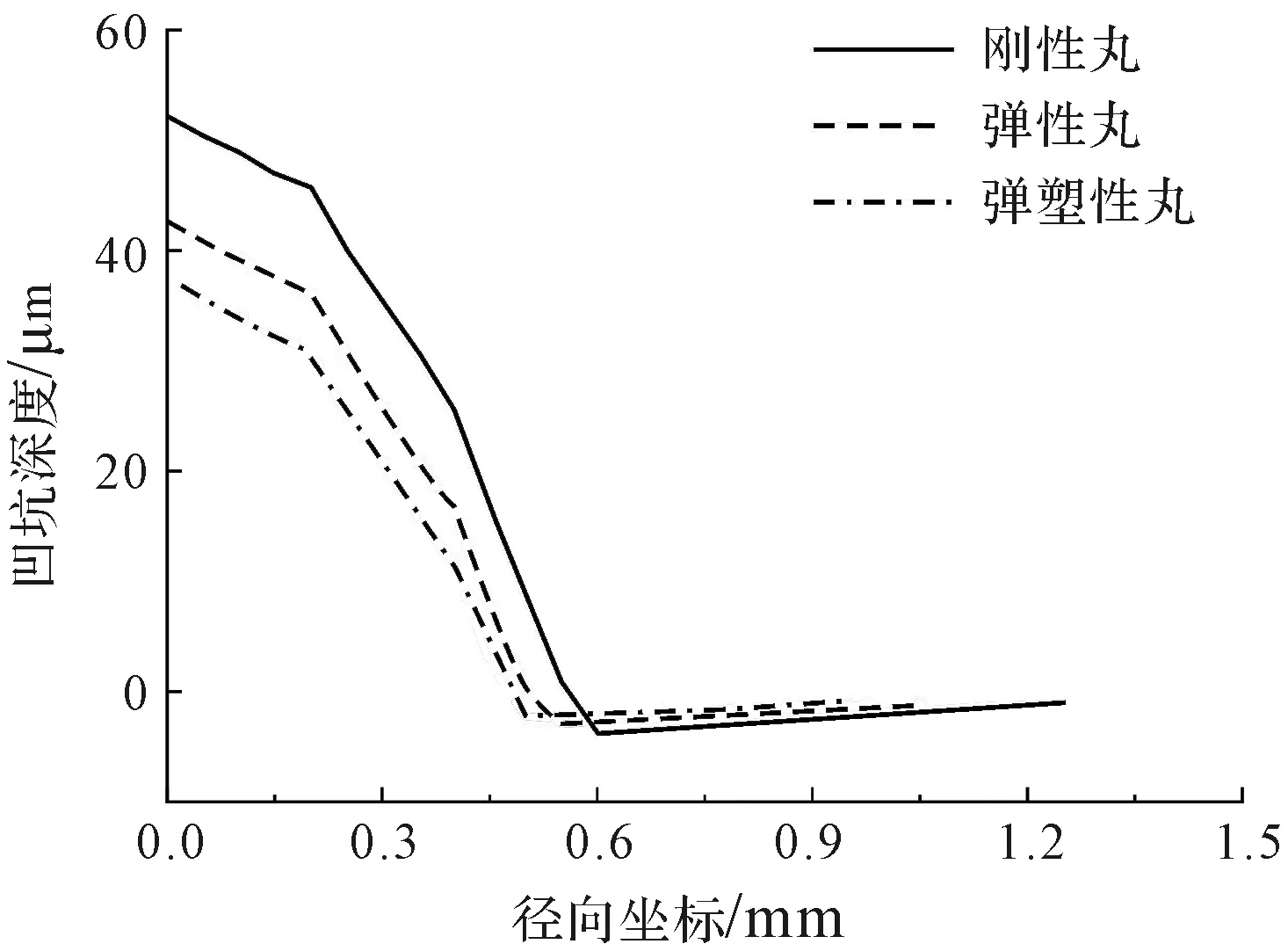
图13 不同材质弹丸冲击纯铜形成的凹坑形貌

由图13可知:1)在相同的超声喷丸工况下,刚性丸冲击纯铜试样形成的凹坑深度最大,弹性丸冲击纯铜试样形成的凹坑深度次之,弹塑性丸对应的凹坑深度最小;2)刚性丸冲击形成的凹坑边缘凸起高度最大,弹性丸冲击形成的凹坑边缘凸起高度次之,弹塑性丸冲击形成的凹坑边缘凸起高度最小;3)相对于凹坑深度的变化,弹丸形变对凹坑边缘凸起高度的影响明显偏小。

3.2.2 残余应力在试样厚度方向的分布

刚性丸、弹性丸和弹塑性丸冲击纯铜试样诱导的残余应力在试样厚度方向的分布情况,如图14所示。

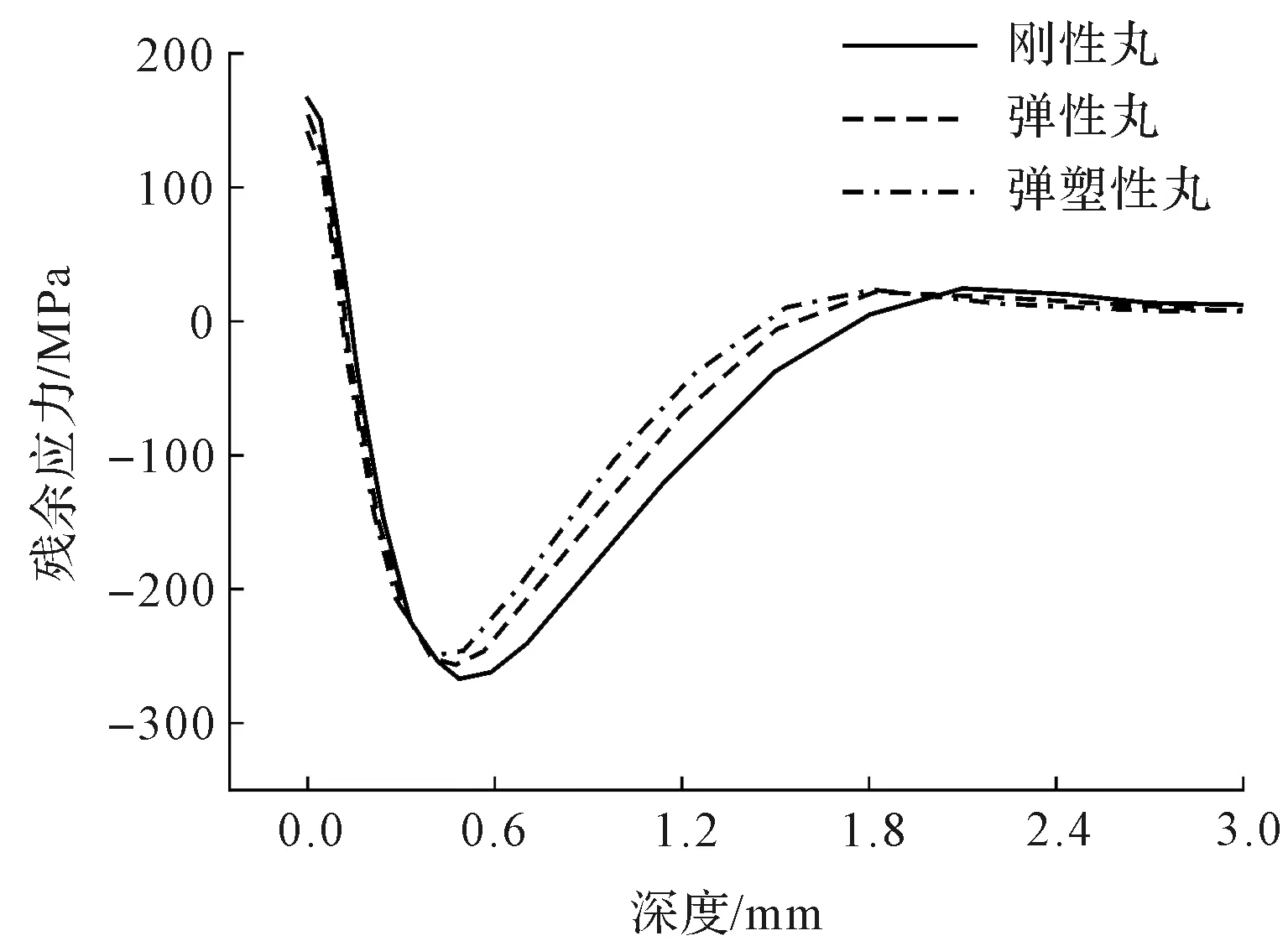
图14 不同材质弹丸冲击纯铜形成的残余应力分布

由图14可知:1)刚性丸冲击纯铜试样形成的残余压应力深度、最大残余压应力和表面残余拉应力均最大;2)弹性丸冲击纯铜试样形成的残余压应力深度、最大残余压应力和表面残余拉应力均次之;3)弹塑性丸对应的残余压应力深度、最大残余压应力和表面残余拉应力均最小。

产生该现象的主要原因是弹丸与纯铜试样的接触刚度不同,接触刚度越大,凹坑尺寸、残余压应力、最大压应力、表面残余拉应力越大。

3.2.3 速度和等效塑性应变

刚性丸、弹性丸和弹塑性丸在冲击纯铜试样后的速度和等效塑性应变情况,如图15所示。

图15 冲击试样后的速度和等效塑性应变

由图15可知:1)刚性丸和弹塑性丸回弹的速度均为1.8 m/s,弹性丸的回弹速度为2.0 m/s,略大于刚性丸和弹塑性丸的回弹速度;2)刚性丸冲击诱导纯铜试样产生的等效塑性应变最大,弹性丸次之,弹塑性丸最小,这与纯铜试样厚度方向分布的残余应力相一致。

因此,在超声喷丸冲击纯铜试样过程中,刚性丸用于纯铜塑性变形的冲击能量最大,诱导的残余压应力深度、最大残余压应力以及表面最大参与拉应力最大。

弹塑性丸将一部分的冲击能量用于自身的塑性变形,如图15(f)所示,导致弹塑性丸的回弹速度小于弹性丸;同时,弹塑性丸冲击纯铜产生的最大等效塑性应变也小于弹性丸冲击的结果,进而形成的残余压应力深度、最大残余压应力和表面残余拉应力均小于弹性丸冲击的结果。

4 结束语

在已有的超声喷丸有限元模型中,绝大多数都忽略了弹丸的弹性、塑性变形对数值模拟结果所带来的影响。同时,关于弹丸表面与受喷材料表面之间的摩擦因数对超声喷丸数值预测结果的影响规律,目前也鲜有报道。

为此,笔者以纯铜试样为研究对象,建立了单丸粒超声喷丸纯铜三维有限元模型,结合超声喷丸实验和数值模拟过程,研究了摩擦因数与弹丸形变对超声喷丸纯铜的影响规律,并对有限元模型的有效性进行了验证。

研究结果表明:

1)单丸粒超声喷丸纯铜三维有限元模型预测的凹坑形貌和弹丸冲击速度与实验测试结果吻合较好;

2)喷丸距离对于单丸粒超声喷丸模拟结果影响很小,可忽略不计;

3)当弹丸与纯铜表面之间的摩擦因数大于0.2时,超声喷丸纯铜形成的凹坑形貌和残余应力对摩擦因数不再敏感;

4)刚性丸与试样接触刚度最大,弹性丸次之,弹塑性丸最小;冲击形成的凹坑尺寸、残余压应力、最大压应力、表面残余拉应力与接触刚度正相关。

在后续工作中,笔者将开展多丸粒超声喷丸的数值模拟和实验研究,以探究超声喷丸工艺参数对喷丸结果的影响规律。