直驱式涡旋机接触力控制方法研究*
方 颢,蔡炯炯,瞿 晓,董桂丽,屠凯莉
(浙江科技学院 自动化与电气工程学院,浙江 杭州 310023)
0 引 言
涡旋机的原理和结构是1905年由法国工程师CREUX L[1]正式提出,并且在20世纪80年代得以发展起来的一种新型容积式压缩机。它的核心部件为动涡盘和静涡盘。
涡旋机的动涡盘和静涡盘的型线组成相同,两者相位旋转180°安装,形成若干封闭的月牙形工作腔,通过各个工作腔的容积变化来完成气体的压缩工作。
涡旋式压缩机普遍采用间隙密封技术。这种技术可以增加涡旋压缩机的可靠性。但是其间隙过大,会产生不必要的泄漏;间隙过小,又会使零件不能正常配合运转,阻碍涡旋压缩机往高压力和大容量的方向发展[2-4]。
为了解决涡旋机工作过程中的泄漏问题,近年来,国内外许多学者提出了涡旋机的泄漏模型以及密封方案。
RONG C等人[5]建立了涡旋机的切向泄漏模型和径向泄漏模型,研究了不同间隙下的泄露损失以及压缩效率的变化规律。查海滨等人[6]针对实际的涡旋压缩机原型,拓扑出了几何模型,并运用一种复合的网格构建方法,建立了计算流体力学(computational fluid dynamics,CFD)模型,对其气体泄漏进行了建模。王建吉等人[7]对涡旋齿3种密封结构(齿顶光滑间隙密封、齿顶迷宫密封以及齿顶组合密封)进行了研究和对比,最后提出了一种新型径向组合密封结构。李海生等人[8]对涡旋齿顶的聚四氟乙烯密封条做了有限元分析,为涡旋压缩机密封条的设计提供了新方法。叶剑等人[9]针对压缩机的切向泄漏问题,提出了一种切向密封结构,以此来减少压缩机泄漏,该结构还改善了压缩机增压过程性能。
上述针对涡旋机密封的研究方案都是从结构和材料上入手,属于被动密封方案。动静涡盘之间的机械耦合较为紧密,计算和建模较为复杂,而且学者们对于密封过程中动静涡盘所产生的接触力的研究也较少。
针对上述研究的不足之处,颜禧龙等人[10]提出了一种用于涡旋压缩机侧面密封的主动控制方法,并分别建立了冷态和热态下动涡盘平动轨迹的数据库。涡旋机根据数据库里的轨迹点进行运动,减少了动涡盘平动过程中的接触力。史策等人[11]针对涡旋压缩机工作过程中接触力可能过大的问题,提出了一种永磁随变机构,当涡旋压缩机的接触力过大时,该机构可以对其进行柔性抵抗,从而减少接触力。
上述研究虽然有效减少了涡旋机工作过程中的接触力,但从力的控制角度上来说属于开环控制,其没有进行力的反馈,得到的控制效果不够直观。
物体之间既要发生接触,同时为了顺从环境的约束,还要精确地控制物体之间的接触力,避免过大的冲击力对物体造成损害。柔顺控制可以实现对力的有效控制目的。柔顺控制可分为两种,即主动柔顺控制和被动柔顺控制。
物体间可以通过安装具有柔顺控制功能的装置(如弹簧、气缸、阻尼器等)来被动调节接触力,称为被动柔顺控制[12],该方法需要增加额外的被动柔顺装置,且不具备控制能力,适用范围受到限制。主动柔顺控制是根据力的反馈信息,采取一定策略对物体间的作用力进行主动控制。与被动型的控制相比,主动控制省略了部分机械装置,降低了耦合度;但少了这些约束后,对其控制器的设计要求变高了。
主动柔顺控制在航空叶片、汽车零部件等大型工件的磨削抛光加工等领域应用广泛。赵源等人[13]在螺旋桨的磨削任务中,使用非线性比例-微分(propor-tional differential,PD)控制器进行了接触力仿真和实验,分析了约束条件下阻抗参数的调节和环境刚度的变化对接触力控制精度的影响。KIGUCHI K等人[14]针对未知环境的抛光任务,设计了基于模糊神经网络的力位混合控制器,采用仿真的方式对该控制器的有效性进行了评估。BUCHLI J等人[15]针对复杂的环境加工任务,采用了基于强化学习的变阻抗控制,结果表明,可变阻抗控制的功率可应用于各种各样的机器人系统和实际场合。NAZMARA G等人[16]设计了基于梯度下降法的模糊控制器,用来调整阻抗控制器的参数,其可用于有障碍环境下的轨迹规划。
动涡盘与静涡盘保持接触是涡旋机进行正常工作的必要条件,否则会导致气体泄漏,影响涡旋机的工作效率;但同时,涡盘间接触压力过大会导致过摩擦现象发生,影响涡旋机的使用寿命。因此,把涡盘间的接触力控制在合理的范围内非常重要。
目前,学者们对于涡旋机侧面接触力的主动控制研究相对较少。除了在工件的打磨、抛光、去毛刺等领域以外,只要涉及物体之间需要发生接触的场合,且产生的接触力需要控制或者需要平稳过渡的场合,就可以采用主动柔顺控制。
因此,针对涡旋机的工作环境,笔者提出一种基于法向-切向坐标系下的主动柔顺控制方法,以对动涡盘和静涡盘之间的接触力进行控制。
1 动涡盘工作空间与接触力
直驱式涡旋机平台的工作部件示意图如图1所示(通过平面电机来控制动涡盘的位置)。
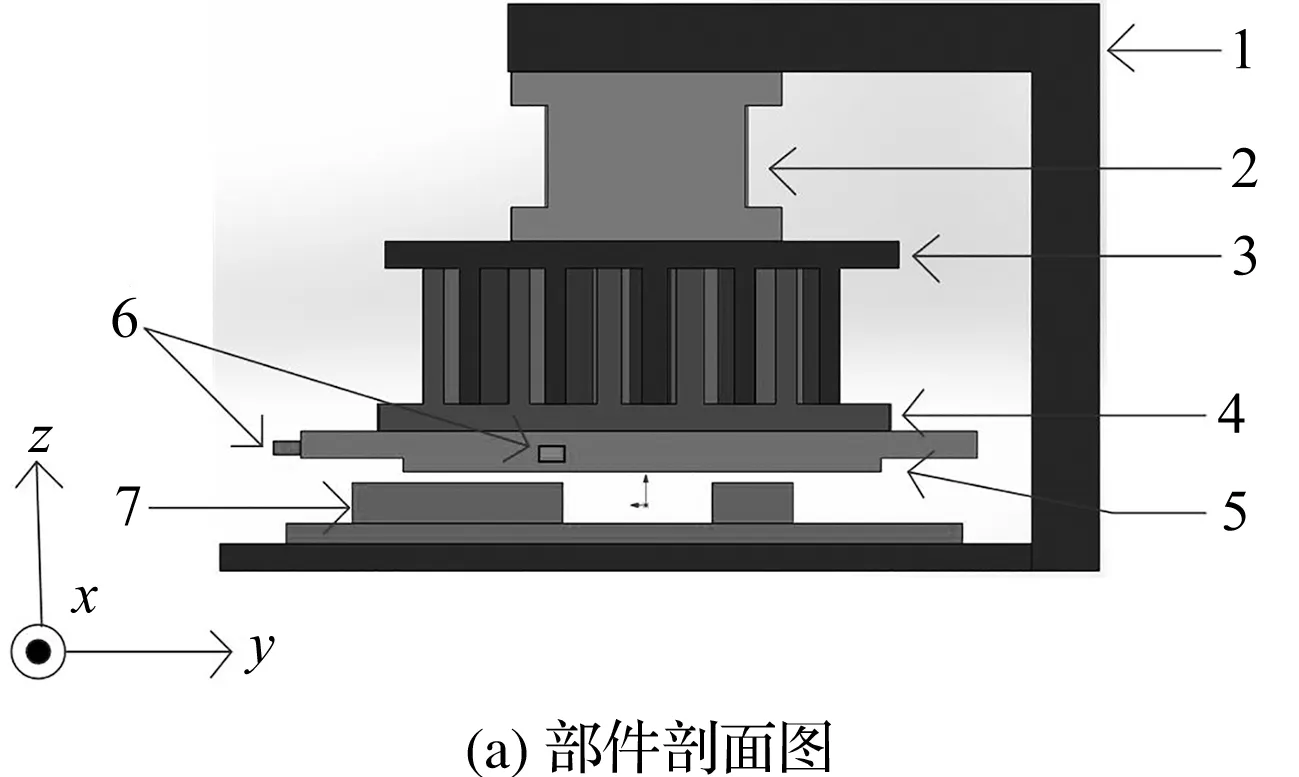
图1 涡旋机的工作部件示意图
由图1(b)可知:平面电机线圈分为2组,一组为X方向,另一组为Y方向,其均固定在平台上。X方向线圈和Y方向线圈通电后,其产生的磁力与永磁体自身的磁力相互作用,从而对永磁体产生X方向和Y方向的推力。
由于永磁体与动涡盘相互固定,所以永磁体运动的同时会带动动涡盘运动,从而改变动涡盘的位置。当动涡盘与静涡盘发生接触时,控制器会根据力的反馈信号对动涡盘的位置进行调整,通过改变动涡盘的位置来改变接触力大小。
动涡盘的平动轨迹为圆形,其当前位置与平动轨迹原点的距离称为平动半径,记作r,如果动涡盘与静涡盘侧面刚好接触,此时的平动半径称为额定平动半径,记作r0。
当r≤r0时,动涡盘和静涡盘之间不会产生接触力;当r>r0时,静涡盘由于受到动涡盘的挤压而变形,从而给予动涡盘一个反作用力。
反作用力矢量可分解成法向和切向2个分量,如图2所示。

图2 动涡盘的受力示意图
图2的左半部分中,静涡盘的形变量为r-r0,一般接触模型用弹簧模型来表示[17-18],因此,平动半径与法向接触力fcn、切向接触力fct的大小的关系如下式所示:
(1)
(2)
式中:k0为涡盘的刚度系数;μ为摩擦系数。
切向接触力fct可看作是动涡盘平动过程中所受的摩擦力。笔者将其与fcn简化成线性关系。
由于法向接触力与平动半径的关系明确,所以需要对动涡盘所受的法向接触力进行控制。
2 柔顺控制模型
2.1 经典柔顺控制方法
在单自由度运动中,物体之间的接触力与位置的关系如图2右半部分所示。其中,x为物体当前位置;x0为临界接触位置。
与式(1)、式(2)类似,x,x0,fc之间的关系如下式所示:
fc=k0(x-x0)
(3)
经典柔顺控制的框图如图3所示。
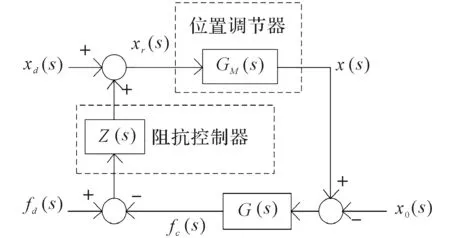
图3 柔顺控制的基本框图
假设此时物体处于过接触状态,由图3可以推导出fc与fd,xd,x0的关系,如下式所示:
(4)

式中:M为期望的惯性系数;B为期望的阻尼系数;k为期望的刚度系数;一般把GM(s)看作一个低通滤波器。
若fd为常量,在保证系统稳定的前提下,fc最终会收敛至fcss。fcss的计算方法如下:
(5)
式(5)中,假设位置控制器能实现位置的零误差跟踪,则GM(0)=1。
由式(5)可知,k的取值会影响接触力的最终收敛值。为了更好地分析M和B的取值对系统的影响,笔者将式(4)中的Z(s)按照标准二阶传递函数的形式表达如下:
(6)
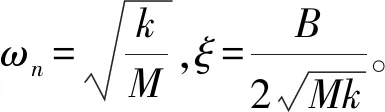
ωn越大,系统的收敛速度越快,但ωn过大会使系统不稳定;ξ过大会引起输出的超调量增大,同时使系统的收敛速度变慢,减小ξ可以使超调量减小,但过小的ξ同样会使系统的收敛速度变慢。
2.2 基于法向-切向坐标下的柔顺控制方法
笔者将动涡盘的二自由度平面运动分解成2个独立的单自由度运动,并分别使用经典柔顺控制方法,再把动涡盘的当前位置和临界接触位置等变量分别投影到XY坐标轴上,如图4所示。
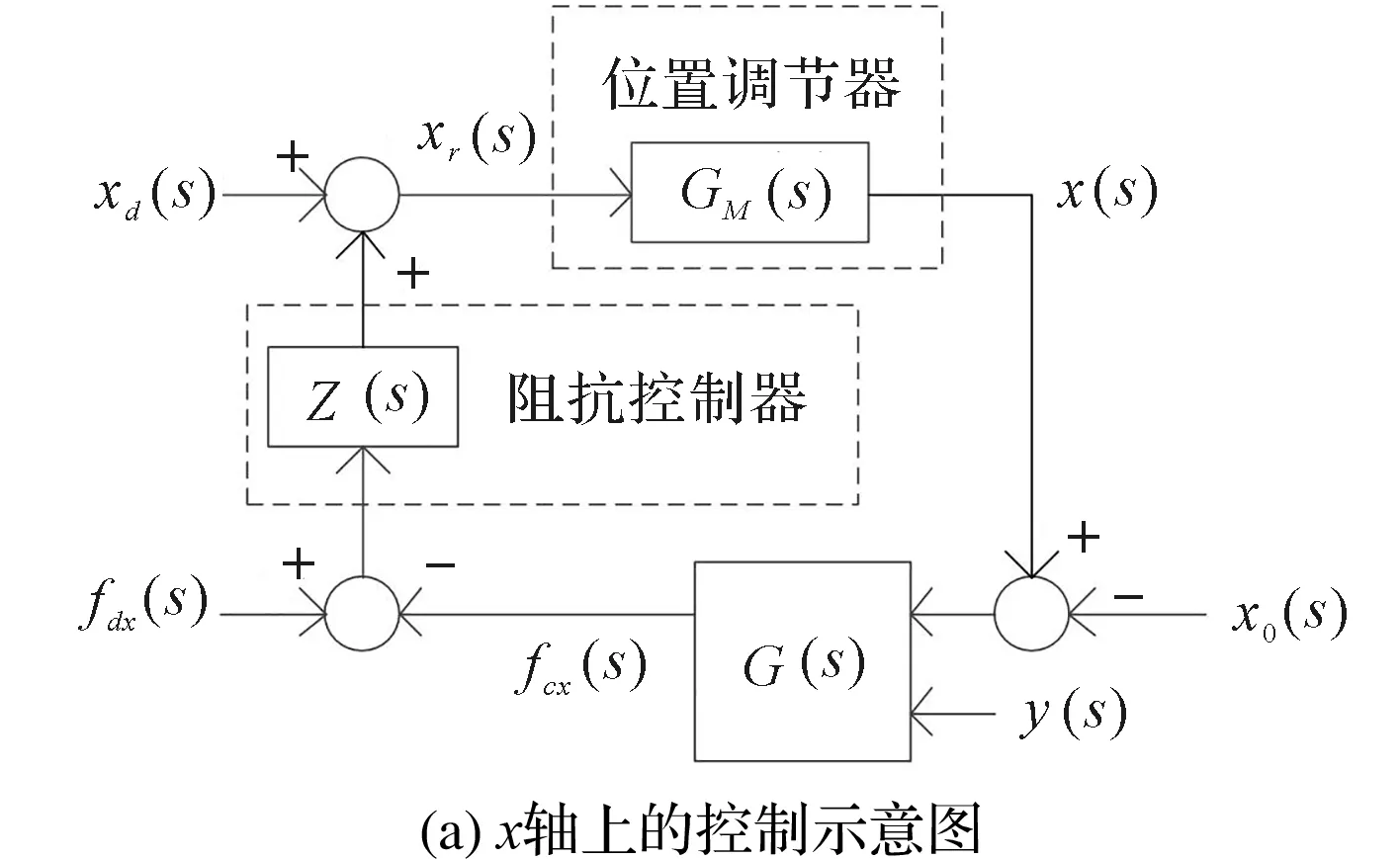
图4 XY坐标下柔顺控制示意图
在动涡盘绕圆周进行平动过程中,接触力矢量在x轴上的投影分量大小不仅与动涡盘位置的x值有关,还与动涡盘位置的y值有关;接触力矢量在y轴上的投影分量大小不仅与动涡盘位置的y值有关,还与动涡盘位置的x值有关。因此,接触力矢量在2个轴的分量大小之间存在耦合。
动涡盘平动过程中,图4中的传递函数G(s)的表达式是一直在变化的,直接用于计算接触力非常困难,因此,需要选择合适的坐标变换来简化计算[19]。
笔者把XY坐标系变换到法向-切向坐标系下,这个坐标系以下简称n-t坐标系。它们之间的变换关系如下式所示:
(7)
式(7)中,θ可以通过下式来表示(x和y为动涡盘在XY坐标系下的位置):
θ=atan2(y,x)
(8)
2个坐标系的位置关系如图5所示(p为动涡盘所在的位置,2个坐标系的原点与平动轨迹的圆心重合)。
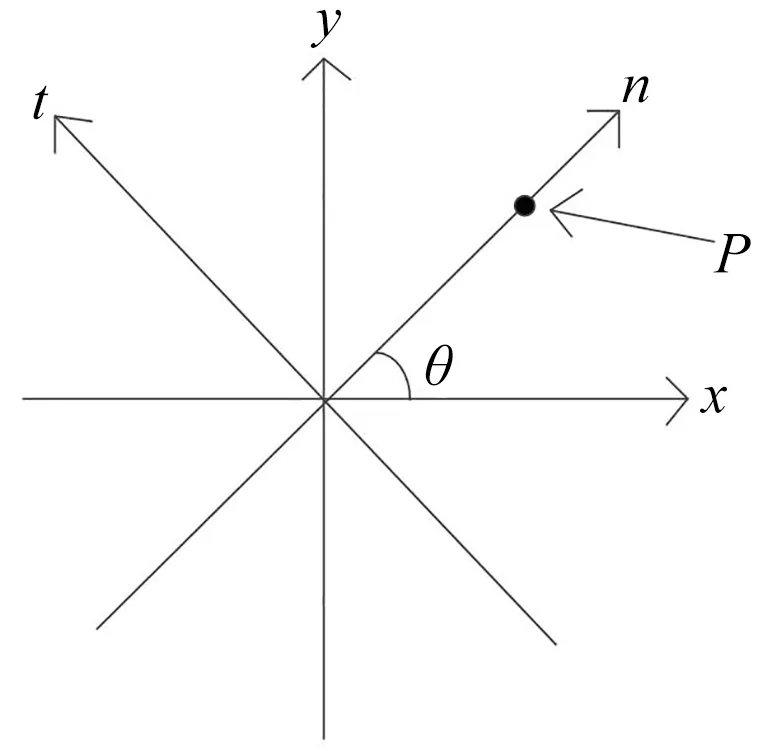
图5 坐标系的位置关系示意图
动涡盘在XY坐标系下的坐标记为(sx,sy),由平动轨迹的圆心指向坐标点(sx,sy)可看作是动涡盘的位移矢量。这个位移矢量在n-t坐标系下的坐标记作(sn,st)。
(sn,st)和(sx,sy)的关系如下式所示:
(9)
式(9)中sn的值代表的是坐标原点到动涡盘的距离,也就是动涡盘的实际平动半径r,所以有sn=r。由式(8)可知st=0恒成立,所以在n-t坐标下只需要考虑sn的值即可。
由于动涡盘与静涡盘刚好发生接触的所有位置点的集合为一个圆,所以在n-t坐标系下,这些位置点的值全部相等。把它们统一记作sn0,且有sn0=r0。
由式(1)可知,位移矢量sn与所受法向接触力的关系如下:
(10)

n-t坐标系下的柔顺控制框图如图6所示。
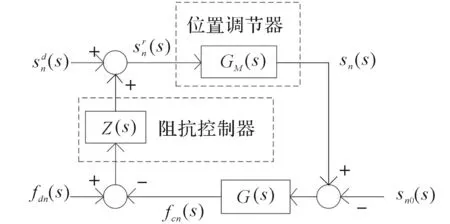
图6 坐标变换后的柔顺控制框图
图6与图3的不同之处在于:图3中的变量以XY作为参考坐标系,而图6中的变量以n-t作为参考坐标系;除此之外,由于传感器的反馈信号是以XY作为参考,因此,笔者需要将这些反馈信号变换到n-t坐标系下进行处理。
3 总体控制方法
笔者以n-t坐标系为基准,描述动涡盘的运动控制方法,以及在该坐标系下的柔顺控制方法。
3.1 运动变量之间的关系
在设计控制器之前,笔者需要知道n-t坐标下质点的位移、速度、推力等变量之间的关系。
在n-t坐标系下,动涡盘平动过程中的速度矢量同样可分解成法向和切向2个分量。其中,速度矢量的法向分量vn>0,意味着平动半径增大,反之减小;速度矢量的切向分量vt>0,意味着平动是按逆时针方向进行的,反之平动按顺时针方向进行。
在XY坐标系下,速度矢量的分量vx、vy与n-t坐标系中的分量vn、vt的关系如下:
(11)
动涡盘所受的推力由平面电机所产生,推力大小与电机的q轴电流大小有关。控制X向的q轴电流记作iqx,控制Y向的q轴电流记作iqy。笔者把q轴电流看作一个矢量,电流的合成矢量在XY坐标系下的坐标为(iqx,iqy),若将该矢量投影到n-t坐标系中,其坐标可表示为(iqn,iqt),iqx、iqy与iqn、iqt的关系,即:
(12)
接触力矢量在XY坐标下的分量fcx、fcy和n-t坐标下的分量fcn、fct的关系如下:
(13)
忽略外部阻力的情况下,动涡盘只受电机所产生的推力以及与静涡盘接触后的接触力影响,所以动涡盘的速度与力的关系如下:
(14)
式中:kf为电机的推力系数;m为动涡盘的质量,两者均为常量。
式(14)两边同时乘以坐标变换矩阵的表达式如下:
(15)
(16)
对式(11)求导后,联立式(11)、式(12)可知,n-t坐标下质点的位移、速度、推力等变量之间的关系如下:
(17)
根据上述的变量定义,使用类似方法可推导出位移矢量的法向分量sn和速度矢量的法向分量vn的关系如下:

(18)
3.2 控制器的设计
假设此时sn>sn0,由式(10)、式(17)、式(18)可知系统的输入、输出关系,由此笔者设计出对应的控制器,如图7所示。

图7 系统的控制示意图
图7中的虚线部分均表示被控对象。由于电流的响应速度比机械运动的响应速度快得多,笔者认为电流控制器的增益恒为1,所以省略对电流控制器的描述。


笔者将图6、图7合并,得到系统的总控制图如图8所示。

图8 系统的总体控制示意图
图8中,由于力传感器的值经过坐标变换后得到的法向接触力为负,因此,笔者需要把这个值乘以-1,然后才能反馈给控制系统。
4 仿真试验
4.1 模型的搭建
笔者使用MATLAB/Simulink搭建了涡旋机的运动控制系统模型(其中包含了平面电机的电流与推力的关系模型);根据式(1)、式(2)搭建了涡盘的接触力模型;根据图8搭建了控制器模型。
接触力模型的参数包括:接触刚度ko和摩擦系数μ。它们的具体数值如表1所示。

表1 仿真参数
4.2 仿真结果
为了验证接触力的可控性,仿真前1 s,笔者令期望的法向接触力为10 N;1 s后令期望的法向接触力突变到5 N,接触力矢量在法向-切向坐标系下的分量值恒为负,直接从传感器获取到的是接触力矢量分别在X轴和Y轴上的投影值。因此,笔者需要把传感器上获得的值进行坐标变换来得到法向接触力的值。
实际法向接触力的值如图9所示。
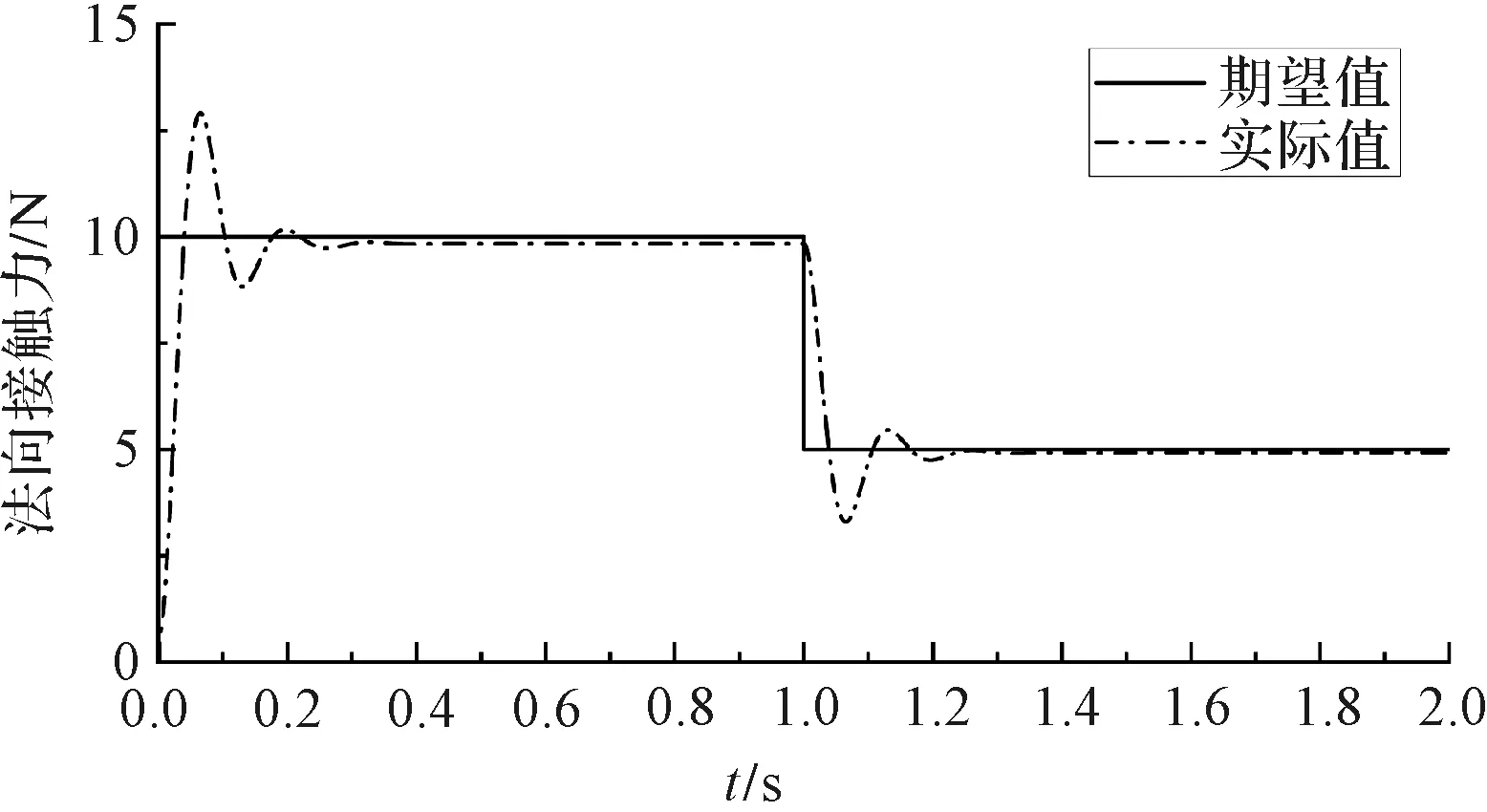
图9 期望值变化时的法向接触力曲线
由图9可知:当期望值为10 N时,实际法向接触力会在一段时间后收敛,收敛值约为9.84 N,相对稳态误差为1.63%;当期望值改变至5 N时,实际法向接触力在0.3 s左右收敛,最终稳定在4.92 N左右,相对稳态误差为1.54%,其误差都在2%以内。
为了验证式(6)中的参数变化时分析结果的正确性,在保持k和ωn不变的情况下,笔者取不同的ξ的值,做出对应的力响应曲线;保持k和ξ不变,取不同的ωn的值,做出对应的力响应曲线,结果如图10所示。

图10 不同阻抗参数下的法向接触力曲线
由图10(a)可知:ξ越小,超调量越大。
图10(b)中,以输出衰减到误差带内且以后不再超出误差带所用的时间来衡量系统的响应速度,可以得知当ωn越大时,系统的响应速度越快。
可以看出:图10中的输出响应与式(6)中阻抗控制器参数对接触力的响应的理论分析结果是一致的。
图9和图10是动涡盘的运动速率在100 mm/s情况下的法向接触力曲线。为了验证动涡盘平动速率突然变化时的法向接触力是否仍然可控,笔者对其进行仿真。仿真前1 s,令vt=100;1 s后,令vt=200,期望的法向接触力恒为10 N。动涡盘的实际平动速率与此时的法向接触力如图11所示。
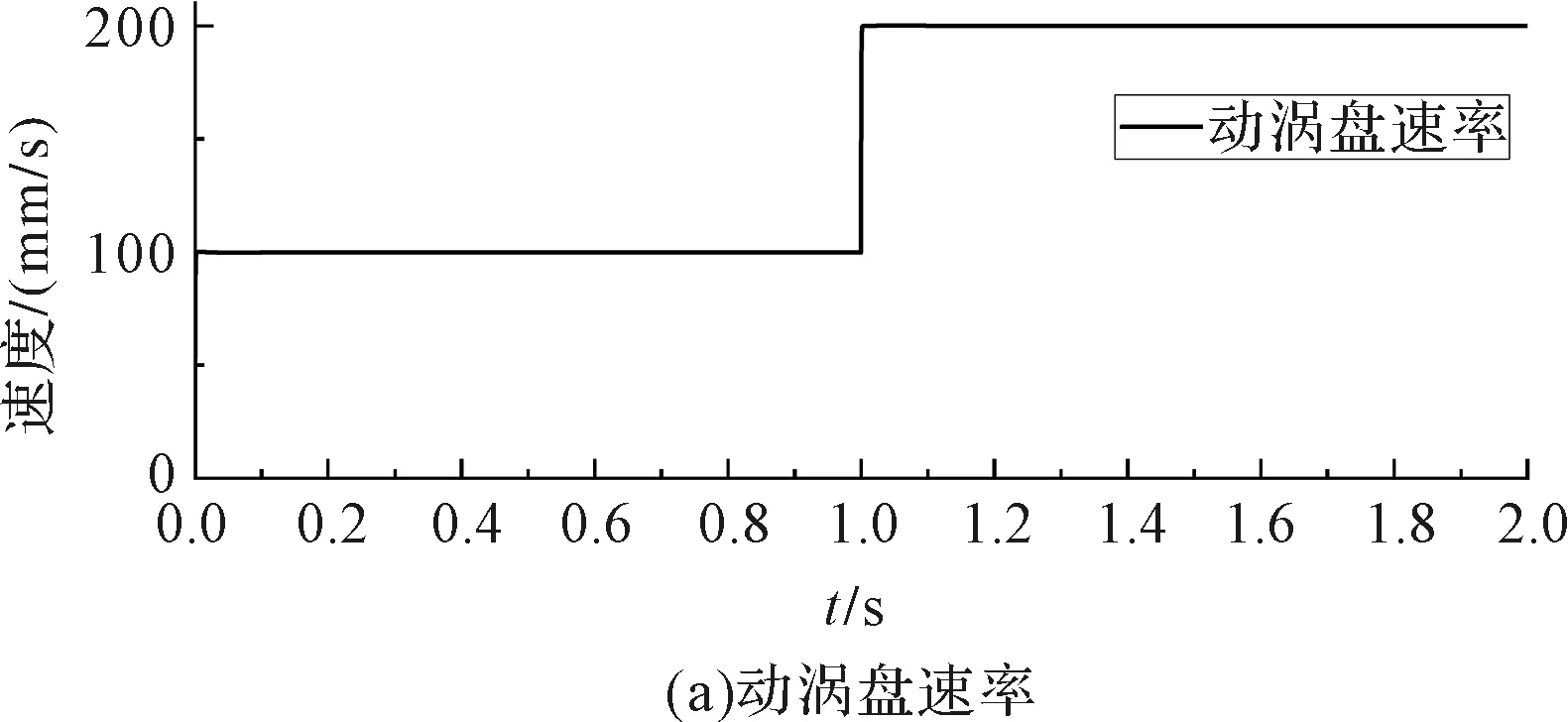

图11 动涡盘速率突然变化时的曲线
由图11可知:当动涡盘的平动速率突然变化时,法向接触力虽然在同一时刻出现了小幅度波动,但在0.2 s之后仍然能向期望值收敛。
5 结束语
针对涡旋机工作过程中动涡盘和静涡盘之间接触力控制困难的问题,笔者提出了一种基于法向-切向坐标系下的主动柔顺控制方法,并设计出了一套在法向-切向坐标系下动涡盘运动系统的控制方案;最后使用MATLAB/Simulink,对动涡盘平动过程中所受接触力进行了仿真验证。
研究结论如下:
1)动涡盘平动过程中,其与静涡盘的法向接触力能收敛至期望值,且误差在2%以内,验证了主动柔顺控制方法的准确性与稳定性;
2)当期望值改变后,法向接触力能在0.3 s左右收敛至新的期望值,说明实际值对期望值的跟踪性能较好,验证了控制方法的快速性;
3)通过调整阻抗控制器的参数,控制系统可以对接触力响应中的超调量以及收敛时间等进行改善;
4)当动涡盘的平动速率突然变化时,法向接触力能在0.2 s左右回到稳定状态,说明控制系统具有一定的抗干扰能力,验证了控制方法有较强的鲁棒性。
在后续的研究中,笔者拟根据涡旋机的实际工况,如接触力的超调量、调节时间以及受到干扰时系统的回复时间等因素,设立具体的评价指标,对阻抗控制器参数做进一步的优化。

