用于稀疏孔径成像系统光程控制的自适应控制算法研究*

钱俊宏,陶 冶,张蓉竹

(1.成都航空职业技术学院 无人机产业学院,四川 成都 610065; 2.四川大学 机械工程学院,四川 成都 610065;3.四川大学 电子信息学院,四川 成都 610065;4.成都凯迪精工科技有限责任公司,四川 成都 610041)

0 引 言

光束干涉成像的3个基本条件是频率相同、振动方向一致和光程差恒定。但由于受环境变化、大气干扰或平台振动等因素的影响,干涉子光束之间会产生较大的光程差,破坏干涉阵列相干成像。因此,想要保证成像质量,就必须对子光束进行实时、快速、高精度的光程调控。

因具有体积小、功耗低、灵敏度高等特点,压电陶瓷被广泛应用于纳米光学、精密仪器和微电子等高精尖领域的光程调控中[1]。但是,由于压电陶瓷控制其材料本身存在迟滞非线性,系统的输出位移会受当前周期与上一个周期的电压输入值影响,使一个电压输入对应2个或多个位移输出[2],令系统出现较大的误差。

对于压电陶瓷的光程控制方面的研究,最先由美国国家标准局的SCIRE F E和TEAGUE E等人[3]开展的。他们利用压电陶瓷材料作为驱动执行元件,制作出了一台压电微位移平台。之后,越来越多的国内外高校和科研院所投入到了压电陶瓷微位移平台的研究中[4-6]。王芳等人[7]以干涉仪中的压电陶瓷相移器为执行元件,基于多项式模型,建立了压电陶瓷迟滞模型,并通过逆模型的前馈控制,实现了微动平台线性矫正的目的;但其未进行系统累积误差的分析。赵新龙等人[8]基于Duhem迟滞模型,建立了系统位移—电压迟滞模型,利用神经网络系统的拟合,建立了压电陶瓷迟滞逆模型;但其未进行相应的实际物理实验。

压电陶瓷迟滞系统的控制策略研究随着迟滞模型的发展不断推进,包括前馈控制、PID控制、复合控制、模糊控制和神经网络控制等[9]。

陈辉等人[10]基于Duhem迟滞模型,建立了压电陶瓷迟滞逆模型的数学表达式,以前馈与反馈相结合的方式设计了仿真实验,证明了该控制方法的有效性;但该研究未进行实际物理实验。王钰锋等人[11]将自适应前馈控制器与PI反馈控制相结合,形成了复合控制系统,提高了系统的泛化能力;但其未将该系统用于光学系统中进行验证。SVECKO R等人[12]结合前馈神经网络和BAT搜索算法,成功提高了模型的位置控制精度。CHEN X等人[13]针对迟滞系统存在的不稳定性,提出了一种自适应控制算法,并通过实验验证了所提控制方法的有效性;但其未进行几个系统的联合控制。

在稀疏孔径成像系统中,需要用到多个压电陶瓷,并与成像结果形成闭环校正。目前主要的闭环校正算法有遗传算法(genetic algorithm,GA)[14]、模拟退火(simulated annealing,SA)算法[15-16]和随机并行梯度下降(SPGD)算法[17-18]等。

IRINA P等人[19]提出了利用模拟退火算法来校正稀疏孔径系统的活塞误差,证明了SA算法在改善系统的点源目标成像质量方面是有效的;但他们只侧重于理论分析,未进行相关实际应用实验。XIE Z等人[20]利用SPGD算法,校正了双孔径稀疏孔径系统中的活塞误差,验证了SPGD算法具有收敛速度快、适用性强、精度高的优势[21];但他们只在实验室理想环境中,基于光学隔振平台进行了实验,并没有针对实际应用的设备进行实验。

针对以上问题,笔者对普通PID的微分项和积分项进行改进,形成一种带滤波器的变速积分PID算法。

笔者将前馈控制与改进PID反馈控制相结合,组成改进的复合控制系统,对单个压电陶瓷进行控制;搭建单个压电陶瓷实验平台,验证“前馈-改进PID反馈”复合控制系统的实际性能;在Golay3稀疏孔径成像系统中,应用SPGD算法完成系统共相误差的校正。

1 前馈控制

压电陶瓷在实际使用时,如果直接对其进行控制,则位移—电压曲线将不会呈现理想的线性关系。在升压和降压时,输出位移存在较大的偏差,并且升压与降压时的输出位移值与期望值都存在差异。这个偏差会给光束的定位和跟踪带来误差,使两束光到达探测器的时间和角度不同,导致成像质量降低,甚至无法成像。

为了解决这一问题,首先需要获得压电陶瓷的迟滞数据。

笔者以德国PI公司生产的S-316.10H压电陶瓷系统为研究对象,其主要性能参数如表1所示。

表1 S-316.10H性能参数

笔者对该系统施加0 V～150 V的驱动电压,并间隔10 V,记录各个电压值对应的位移变形量;再以10 V电压为间隔,将外加电压从150 V降到0 V,记录对应变形量,得到了电压与位移对应数据,如表2所示。

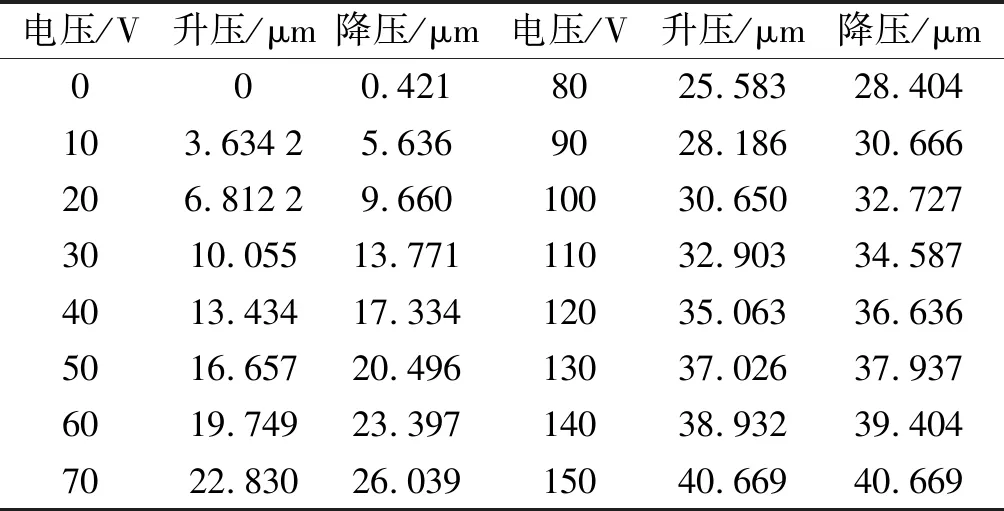
表2 电压与位移对应数据

笔者利用Simulink,将压电陶瓷迟滞逆模型、压电陶瓷迟滞模型、压电陶瓷电容特性以及微动平台的机械特性串联起来,完成了前馈控制系统。

为验证升程与回程2条曲线的控制结果,笔者分别输入信号y=x与y=40-x;将仿真时间设置为40 s,采样频率为20 Hz,得到了前馈控制仿真结果,如图1所示。

图1 前馈控制仿真结果

由图1可知:升程曲线与回程曲线基本为线性,因此,该迟滞逆模型基本能够消除系统的非线性。在刚开始时位置误差是比较小的,但在时间为40 s时,升程误差达到2.5 μm,说明有累计误差存在。

为了解决这一问题,需要引入反馈控制环节。

2 改进的PID反馈控制

为了提高系统的控制精度、响应速度以及抗干扰性能,笔者分别对PID积分项与微分项进行了改进,提供了一种带滤波器的变速积分PID算法。

根据系统偏差大小,变速积分可改变积分项的累加速度,从而实现积分项作用与理想PID控制要求相对应的目的:偏差变大时,积分随之变慢;偏差变小时,积分适当增加。

而在微分控制器中,引入滤波器后,其既能提高系统的动态性能,又能抑制微分项引起的高频信号干扰。

改进的PID控制器积分项表达式为:

(1)

式中:β为关于系统偏差error(k)的函数。

β表达式设为:

(2)

式中:A,B为人为设定的阈值;β的值可在区间[0,1]内变化,根据系统偏差大小来不断地调节积分项的强弱。

笔者在PID控制系统微分环节中引入滤波器,PID控制器的结构图如图2所示。

图2 改进的PID控制器结构图

滤波器可以等效为一个一阶惯性环节,一阶惯性环节可以过滤高频信号。其表达式如下:

(3)

式中:Tf为滤波器系数。

PID传递函数可由下式表示:

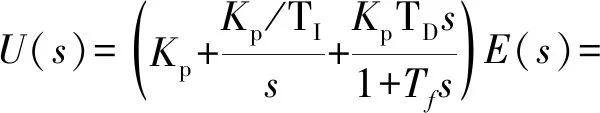
(4)

式中:Kp为比例控制器的比例系数;TI为积分控制器积分常数;TD为微分控制器的微分常数。

微分项表达式为:

(5)

式中:E(s)为系统误差。

将式(5)改写成微分方程形式,即:

(6)

离散化:

(7)

将式(7)整理为:

(8)

式中:Ts为系统采样时间。

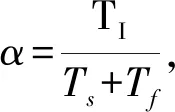
uD(k)=KD(1-α)(error(k)-(error(k-1))+αuD(k-1)

(9)

3 复合控制系统

笔者将迟滞逆模型与改进的PID反馈相结合,形成了复合控制系统。反馈控制器与前馈控制器共同作用于压电驱动器,其中,迟滞逆模型用于前馈回路中,PID控制器用于反馈,其兼具较快响应与较高精度。

“前馈-改进PID反馈”复合控制系统结构如图3所示。

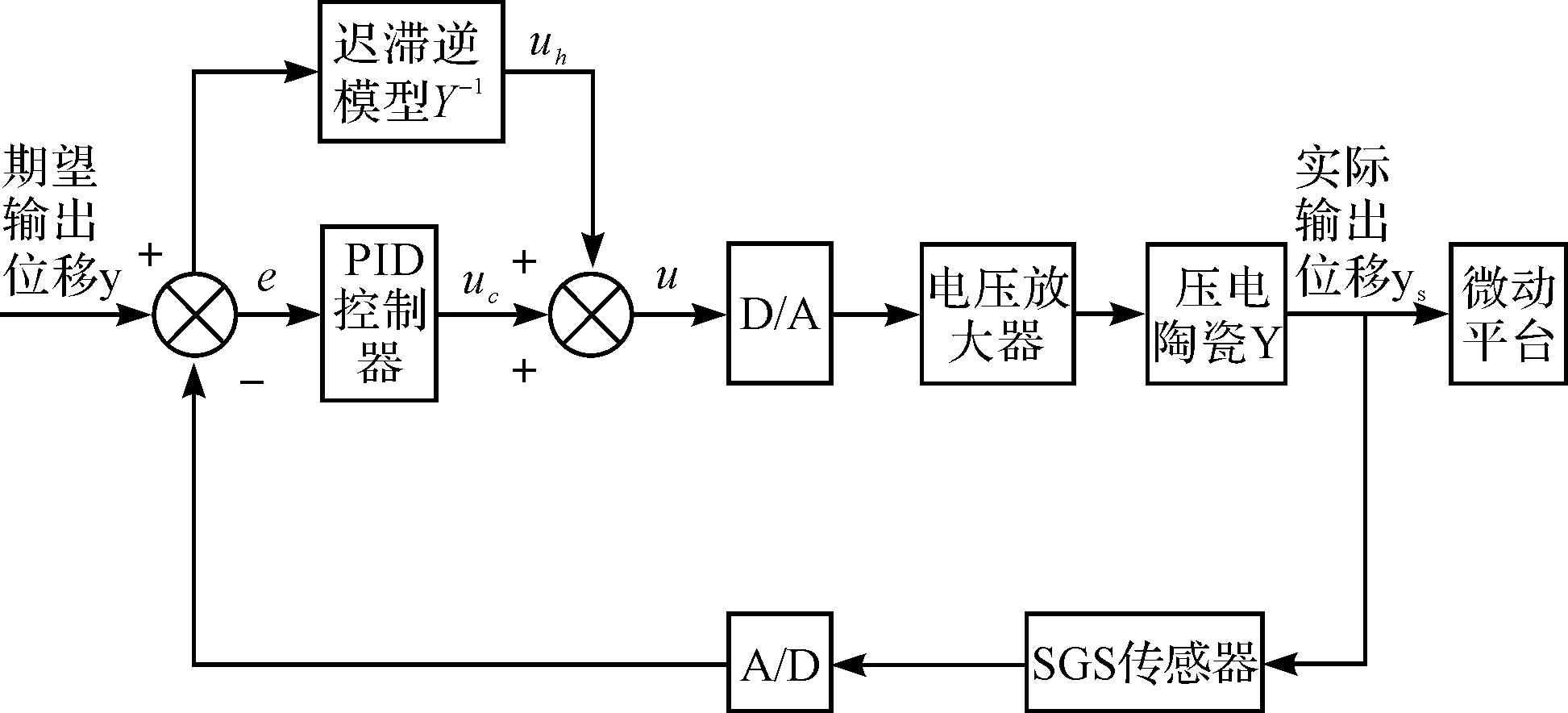
图3 “前馈—改进PID反馈”复合控制结构图

系统控制器输出电压u由2部分组成:即前馈输出uh与PID控制器输出uc。

其中,前馈控制环节输出的补偿电压uh是根据推导出的压电陶瓷迟滞逆模型Y-1和系统的输入值y得到的;PID反馈控制输出的偏差电压uc是由输入值和输出值的偏差量e得到的。

为了验证改进后的复合控制策略可以有效提高控制效果,笔者分别以阶跃信号、斜坡信号和带干扰的阶跃信号为激励信号,进行了仿真实验。

实验过程所用参数值如表3所示。

表3 系统参数值

以阶跃信号作为输入信号时,“前馈-PID反馈”复合控制系统的输入输出曲线如图4所示。

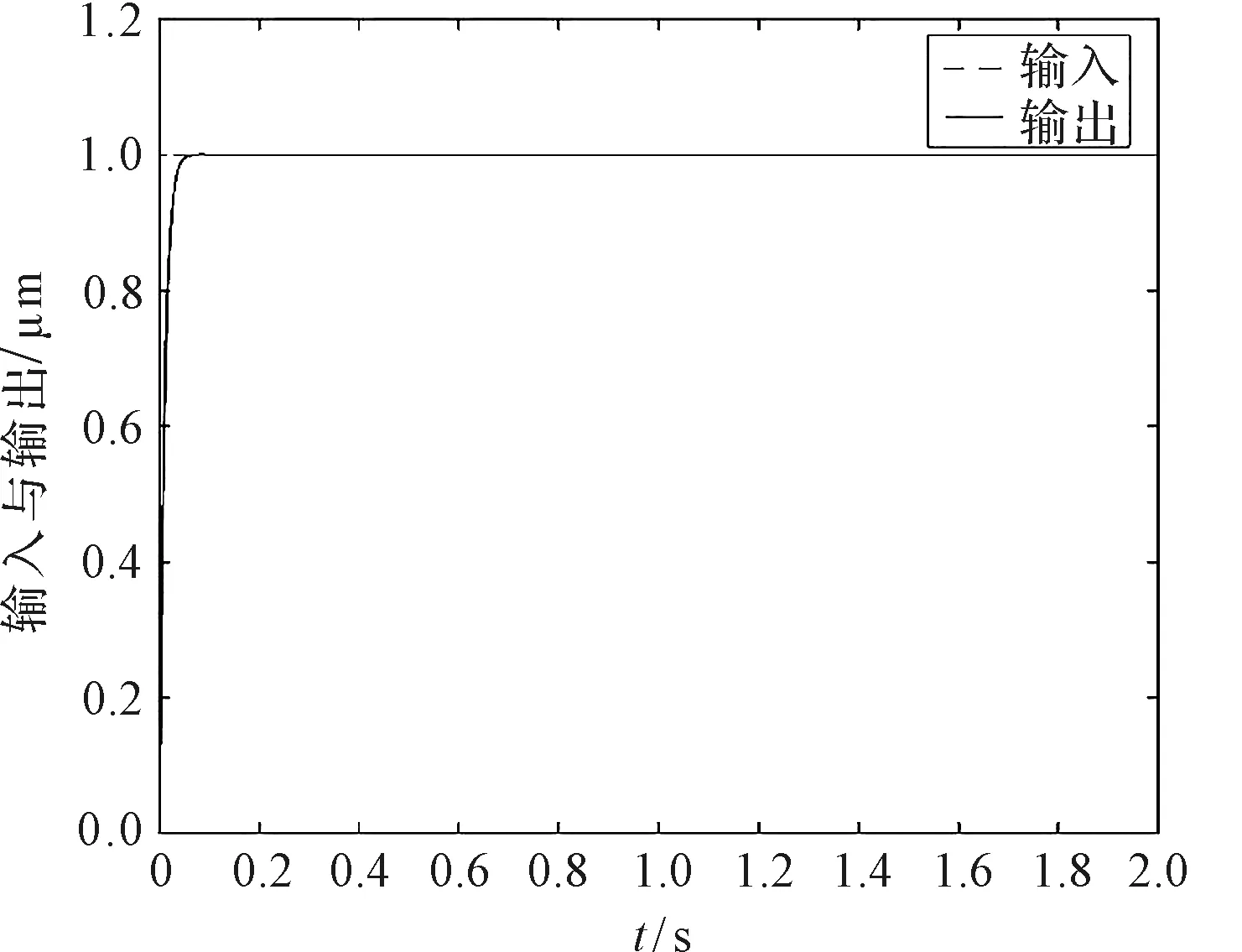
图4 阶跃响应跟踪仿真

从图4可知:系统能在0.06 s内达到稳态。由此可见,复合控制系统的控制精度较高,系统响应速度较快。

笔者以斜坡信号作为输入,令压电陶瓷系统从0位移到10 μm,速度为5 μm/s,得到了系统的响应曲线和误差曲线,如图5所示。

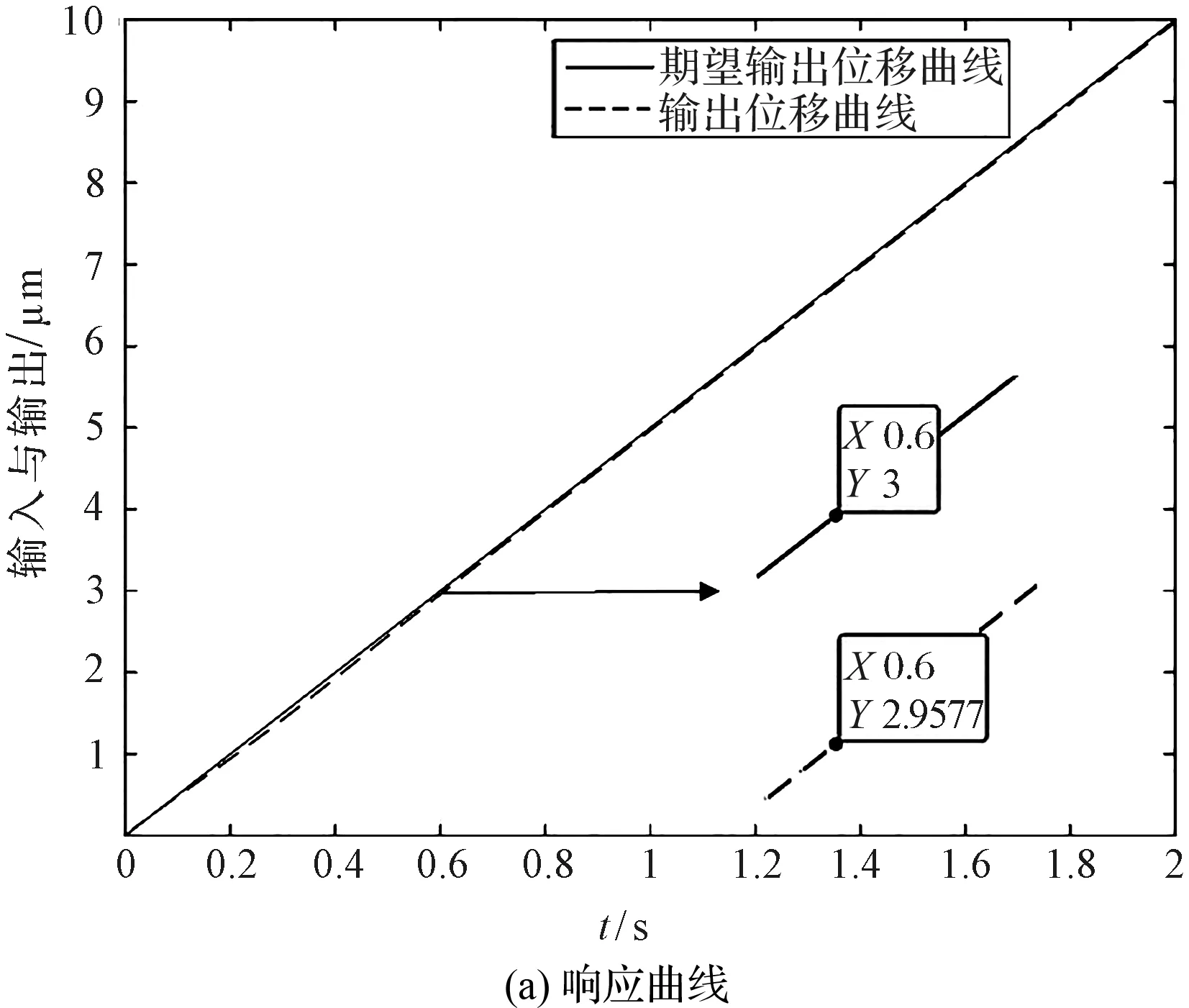
图5 斜坡响应跟踪仿真

由图5可知:“前馈-改进PID反馈”系统在开始跟踪阶段就表现出极稳定的状态,可以快速跟踪激励信号,跟踪误差为4 nm。

可见复合控制系统有较好的动态跟随能力。

当以三角波信号作为输入信号时,“前馈-PID反馈”复合控制系统的最大误差为8.7 nm,如图6所示。

图6 三角波响应跟踪仿真

笔者以带干扰的阶跃信号作为输入(其中,干扰信号幅值为50 nm,频率为1 kHz),得到了其跟踪响应曲线(即抗干扰能力仿真结果),如图7所示。

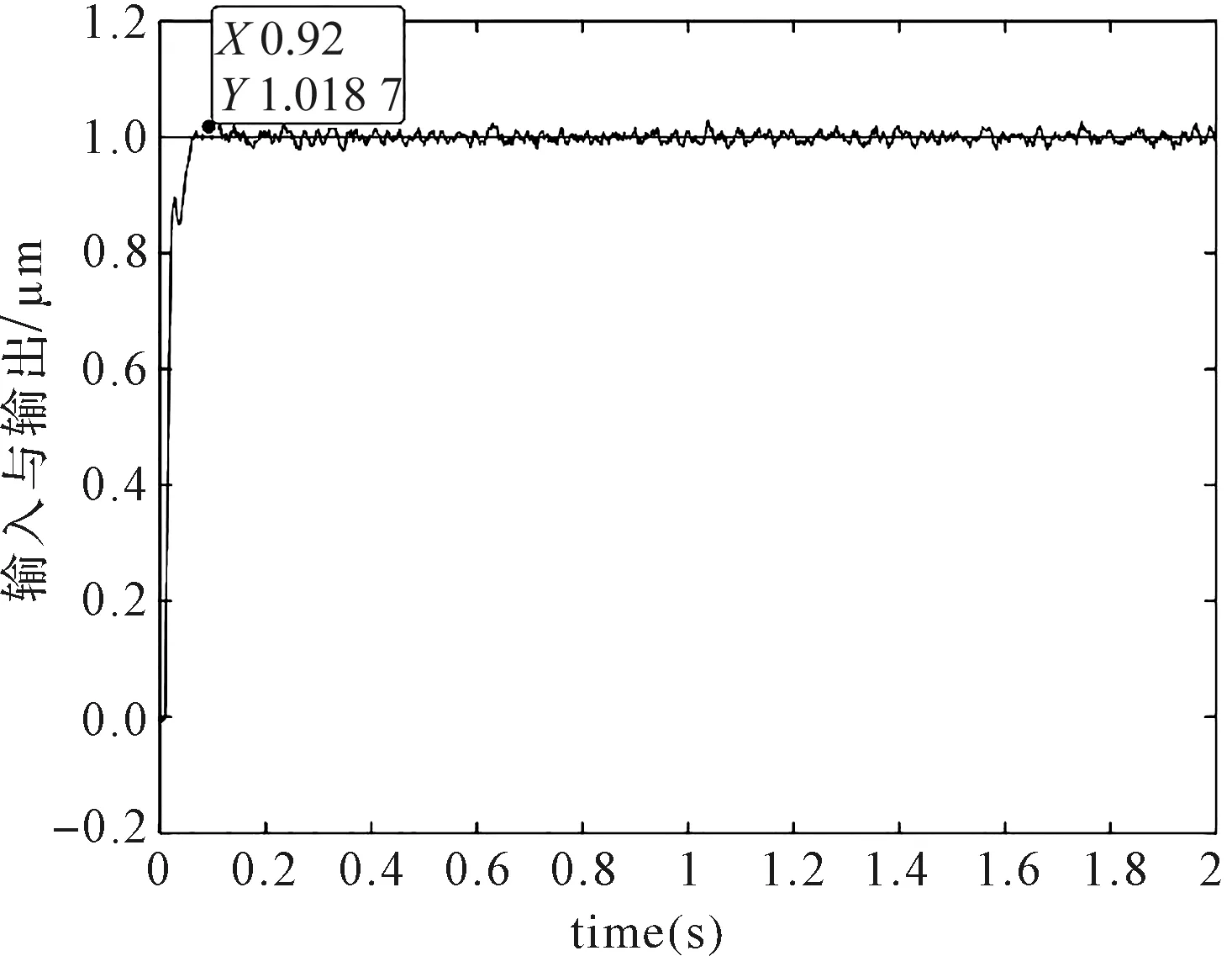
图7 抗干扰能力仿真结果

由图7可知:在加入干扰信号后,“前馈-改进PID反馈”复合系统最大误差为14 nm。

由此可见,复合控制系统具有较好的抗干扰能力。

4 SPGD联合控制优化

Golay3稀疏孔径成像系统中,每一个子孔径都有一个压电陶瓷进行光程调控。各子孔径的光束必须通过一套联合控制系统进行优化,才能达到校正共相误差的目的。

馆藏资源宣传：通过多种途径了解不同类型读者的信息需求，不断补充和完善信息资源建设；多种渠道宣传介绍馆藏，使临床专业人员对馆藏资源的知晓率达到90%。

随机并行梯度下降(SPGD)算法是以成像清晰度为优化目标,采用寻优迭代方法计算各压电陶瓷的驱动电压。

SPGD算法的控制过程图如图8所示。

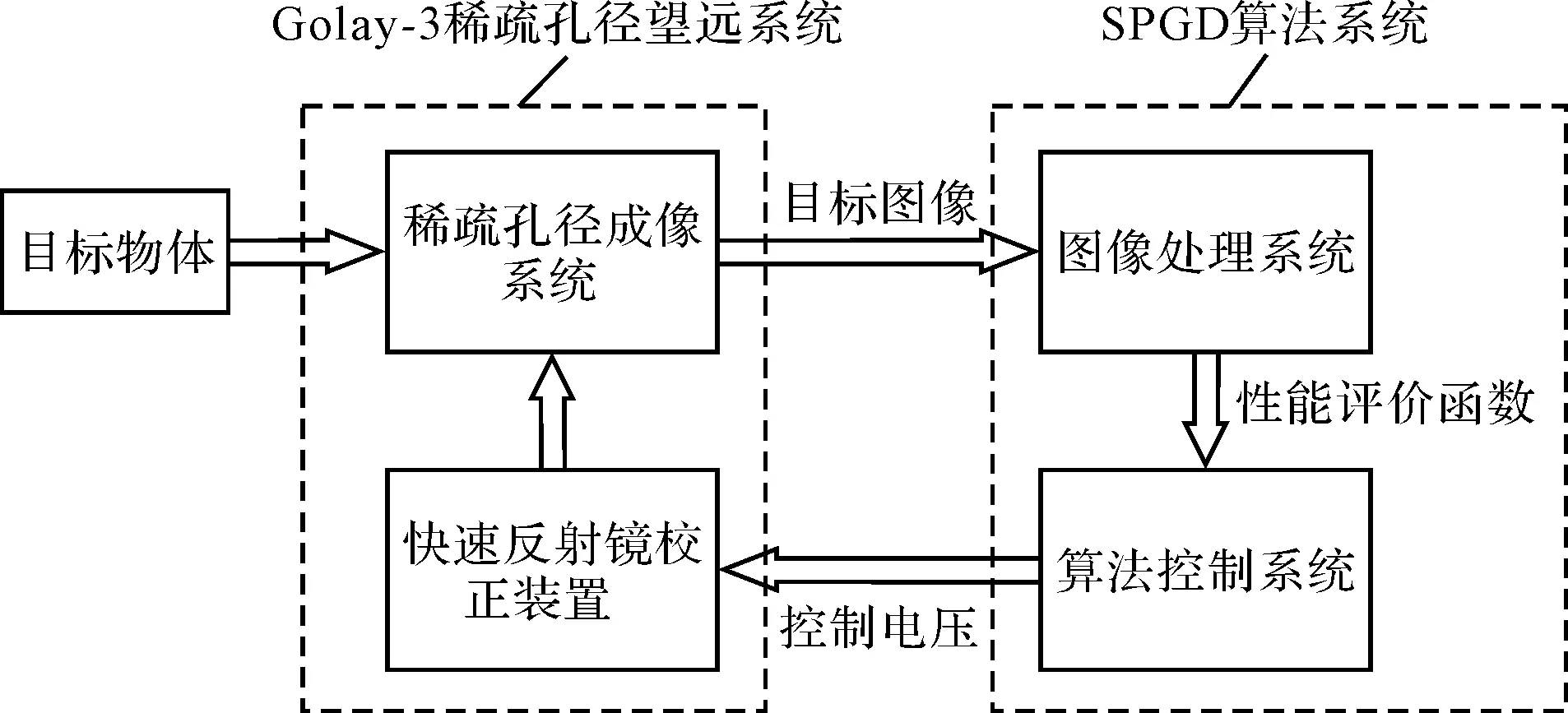
图8 SPGD算法控制过程

笔者选取归一化处理的成像面灰度值的平方和作为性能评价函数J,其表达式为:

(10)

式中:(x,y)为成像面坐标;I(xi,yi)为理想图像灰度值;I(x,y)为实际图像灰度值。

传统SPGD算法采用了固定的增益系数与扰动幅值,从而导致其在实际应用中存在迭代速度慢、稳定性低、参数难以实时调节等问题。

针对稀疏孔径成像系统,笔者在变增益的基础上,提出了一种自适应增益动量SPGD算法。即通过自适应调节增益系数,并引入梯度的二阶动量调控算法,提高了系统的收敛速度和精度;在迭代过程中不断累积梯度的动量,降低了梯度下降的波动。

算法的迭代公式为:

(11)

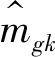
mgk=αmg(k-1)+(1-α)gk

(12)

vgk=βmg(k-1)+(1-β)gk2

(13)

(14)

(15)

式中:mgk为梯度一阶动量,其初值为0;vgk为梯度二阶动量;gk=δuJ为第k次迭代时的梯度估计值;α,β为动量因子。

笔者设置初始增益系数γ0=0.3,随机扰动δu=0.01 v,且服从伯努利分布[21],活塞误差为0.5λ,迭代次数为200次,在单色光(λ=633 nm)点源成像条件下,分别应用自适应增益动量SPGD算法以及传统SPGD算法、文献[22]提出的变增益SPGD算法和文献[23]提出的自适应梯度估计SPGD(adaptive gradient estimation stochastic parallel gradient descent,AGESPGD)算法,对Golay-3稀疏孔径望远系统单个子孔径存在共相误差进行校正。

4种算法的迭代次数k与性能评价函数J的关系如图9所示。

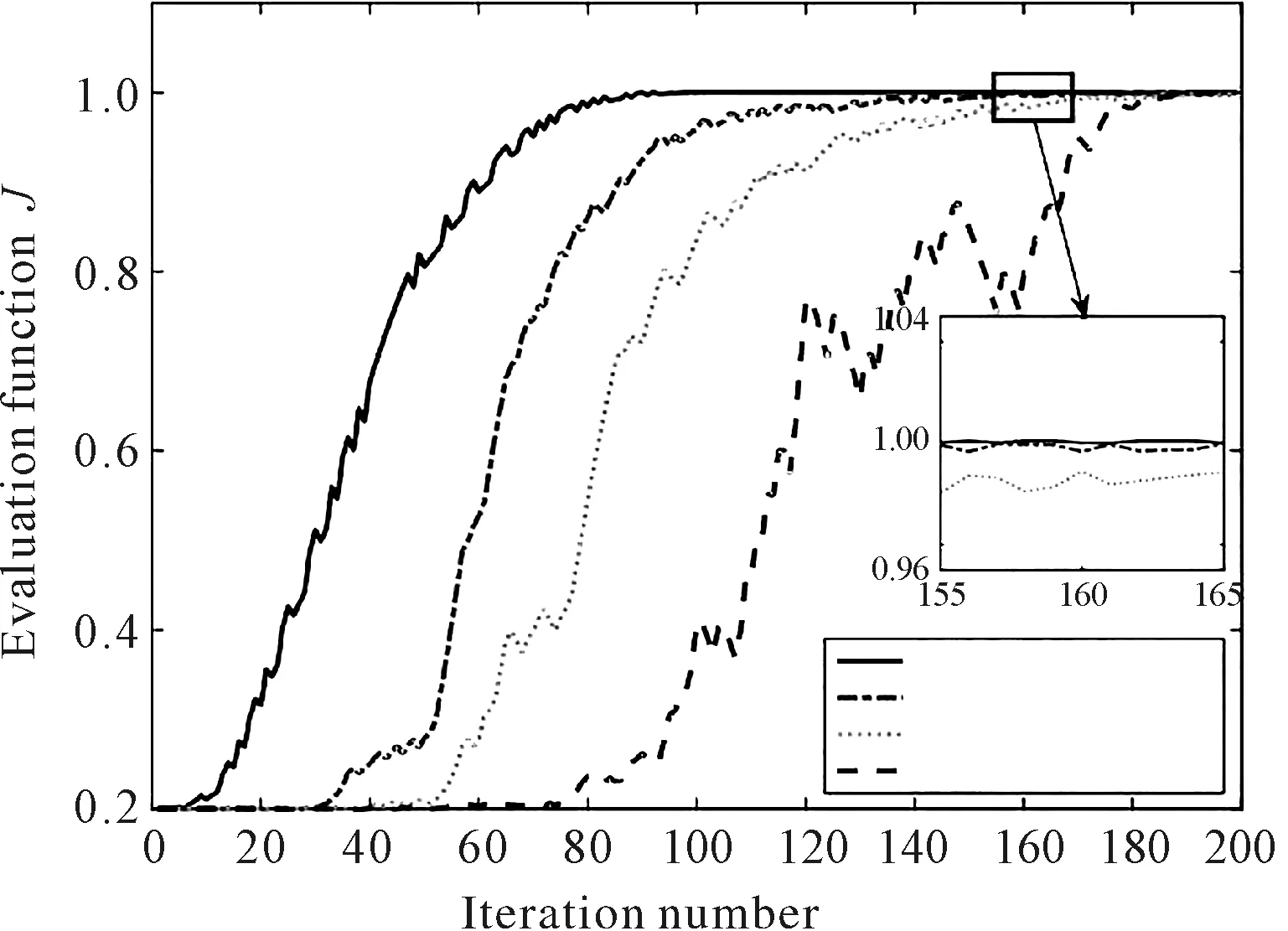
图9 不同算法结果

由图9可知:在迭代200次之后,4种算法均能收敛于极大值,其中,自适应增益动量SPGD算法的收敛速度最快,迭代约90次收敛;AGESPGD算法的收敛速度次之,迭代约150次收敛;变增益SPGD算法迭代约170次收敛;传统SPGD算法迭代约190次收敛。

5 实 验

5.1 单个压电陶瓷位移跟踪实验

实验硬件包括控制模块、执行模块和检测模块3部分。

系统硬件组成框图如图10所示。

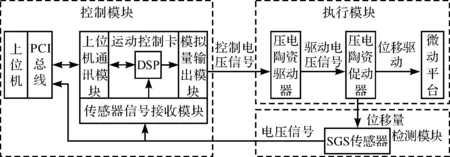
图10 系统硬件组成框图

S-316.10H压电陶瓷、固定架、平面反射镜和装配后的实物图,如图11所示。

图11 执行模块硬件

S-316.10H压电陶瓷内部集成了SGS传感器作为位置传感器检测模块。SGS传感器根据压电陶瓷系统位移量输出电压信号;数据采集卡将模拟量信号放大,转换成数字量输入运动控制卡进行处理。压电陶瓷驱动器采用PI公司适配的E-727.3SDA型驱动器。E-727.3SDA是多通道的数字压电驱动器,可支持3个轴的运动控制,采用D-sub37电压连接,接口与压电陶瓷适配。

笔者选用了美国Power UMAC可编程多轴运动控制器,该控制器提供了多种通讯接口,包括串口、网口和USB口,其可以接收来自控制器的模拟量电压命令,对压电陶瓷系统进行控制;同时,其可以通过该接口反馈模拟量电压信号,监视实际到达位置。

控制模块硬件如图12所示。

图12 控制模块硬件

笔者采用前馈-PID反馈复合控制系统,对压电陶瓷平台进行了1 μm、5 μm、8 μm和10 μm位移跟踪实验,得到了各位移跟踪响应曲线和误差曲线,如图13所示。

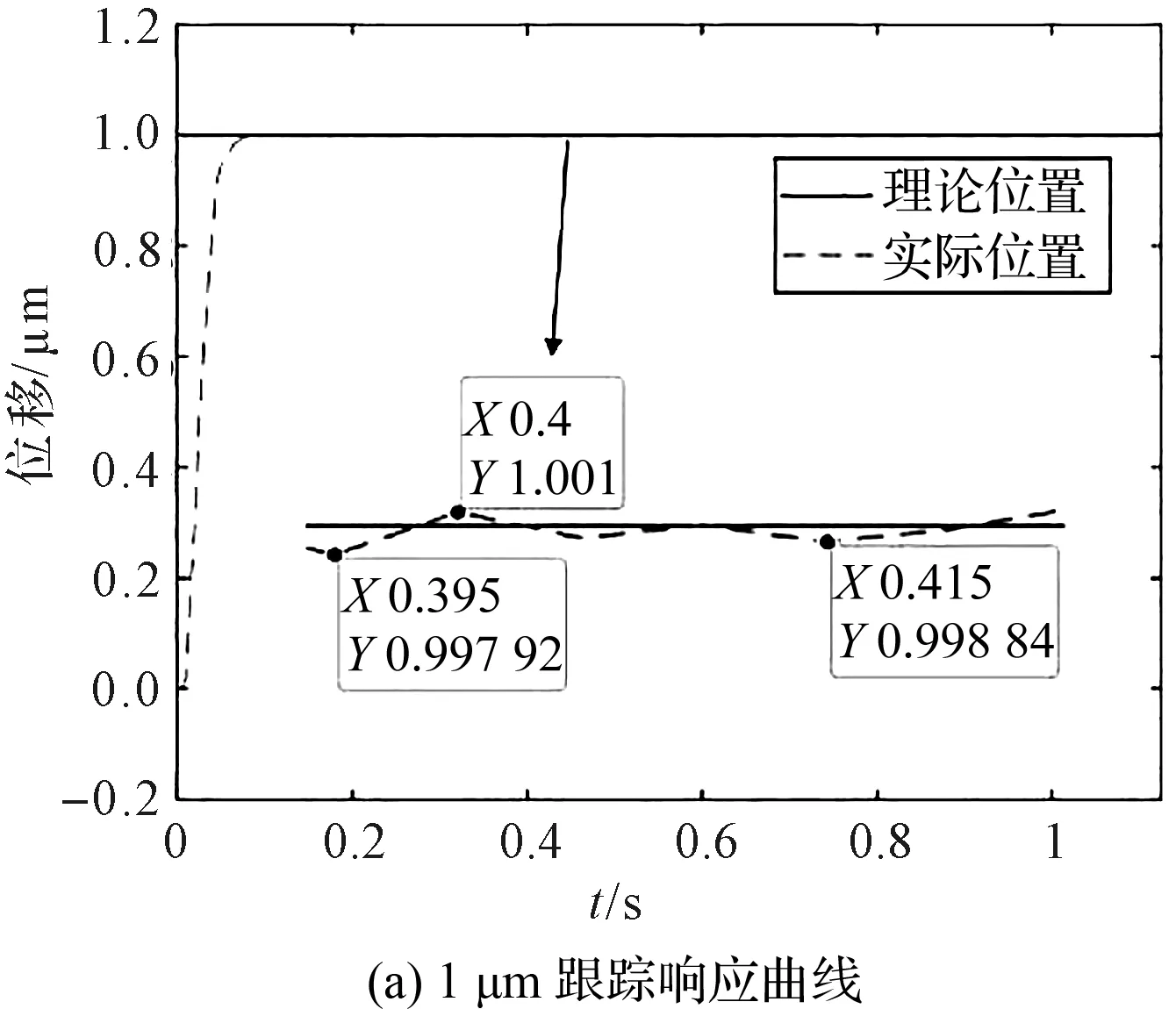
图13 位移跟踪响应实验结果

从图13中可以看出:系统不同位移的响应曲线都基本与期望位移曲线重合;不同位移的响应时间基本在0.08 s以内,控制误差在±3 nm以内(只有在行程无限接近或者达到最大行程时,才有明显的误差)。

5.2 光程调控成像实验

稀疏孔径成像系统的光程调控结构由一个靠压电陶瓷控制的45°倾斜平面反射镜,和一个相对固定的45°角锥反射镜组成,其结构图如图14所示。

图14 光程控制结构图

笔者将3个光程控制应用于1个三孔径成像系统中。系统光程调控实验平台(光路结构和实验物理系统)如图15所示。

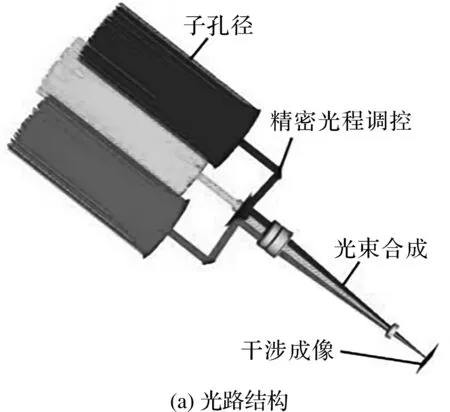
图15 光程调控实验平台

3个子孔径光束需要将Z向误差控制在λ/10,即55 nm,XY倾斜误差控制在0.25 μrad范围内才能在像面干涉成像。在系统的共相误差校正控制中,单个压电陶瓷都采用复合控制,3个压电陶瓷的联合控制采用SPGD算法进行成像清晰度优化。

笔者利用USAF1951分辨率板作为探测目标,得到了联合控制前后成像对比结果,如图16所示。

图16 光程调控成像实验结果

笔者采用式(10)的方法,对共相误差校正前后图像进行了定量评价:校正前,评价值J1=0.54;校正后,评价值J2=0.78。

从实验结果可以看出:采用联合控制系统前,成像结果存在明显的模糊现象;而采用联合控制系统后,共相误差得到了校正,实现了稀疏孔径系统干涉成像目标。

6 结束语

目前,稀疏孔径成像系统共相误差校正存在效果不佳的问题,为此,笔者提出了一种用于光程控制的自适应控制算法。

笔者首先对基于迟滞逆模型的前馈控制进行了仿真,对普通PID进行了改进,并将其与前馈控制组成了前馈-PID反馈的复合控制系统;接着,针对稀疏孔径成像系统中的多个压电陶瓷,以成像清晰度作为优化目标,采用一种自适应增益动量SPGD算法进行了联合控制;然后,对单个压电陶瓷进行了1 μm、5 μm、8 μm和10 μm位移跟踪实验;最后,将SPGD联合控制系统用于稀疏孔径成像系统中,进行了分辨率板跟踪实验。

研究结果如下:

1)前馈控制仿真表明,迟滞逆模型能够基本消除系统的非线性特性;但在时间达到40 s,且升程过程中期望位移为40 um时,系统误差较大;

2)对复合控制系统进行了仿真实验。当输入信号为阶跃信号时,复合控制系统能在0.06 s内达到稳态;当输入信号为斜坡信号时,跟踪误差为4 nm;当输入信号为带干扰的阶跃信号时,最大误差为14 nm;

3)自适应增益动量SPGD算法仿真结果显示,该算法迭代约90次后达到收敛,明显比其他3个算法的收敛速度快;

4)单个位移跟踪实验结果表明,不同位移的响应曲线都基本与期望位移曲线重合,且响应时间能有效控制在0.08 s以内,跟踪误差能有效控制在±3 nm以内;

5)采用SPGD联合控制系统进行了实验,系统共相误差得到了校正,实现了稀疏孔径系统干涉成像目标。

笔者实现了室内三孔径系统干涉成像目标,校正了系统内的共相误差。由于受到系统MTF中频下降因素的影响,成像清晰度有待提高。因此,后期笔者将针对图像去噪声和中频改善开展进一步的研究。